人教版(五四制) 八上 20.4 最短路径问题(2)课件(共17张ppt)
文档属性
| 名称 | 人教版(五四制) 八上 20.4 最短路径问题(2)课件(共17张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 366.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-20 22:37:08 | ||
图片预览





文档简介
第二十章 轴对称
20.4 最短路径问题(2)
一、温故互查
1.已知:如图,A,B在直线l的两侧,在l上求一点P,使得PA+PB最小。
l
有理数:整数和分数统称为有理数
2.如图所示,要在街道旁修建一个奶站,向居民区A、B提供牛奶,奶站应建在什么地方,才能使从A、B到它的距离之和最短.
一、温故互查
3.如图,A、B是直线a同侧的两定点,定长
线段PQ在a上平行移动,问PQ移动到什么
位置时,AP+PQ+QB的长最短?
一、温故互查
(造桥选址问题)如图,A和B两地在同一条河的两岸,现要在河上造一座桥MN.桥造在何处可使从A到B的路径AMNB最短?(假定河的两岸是平行的直线,桥要与河垂直)
思考:
你能把这个问题转化
为数学问题吗?
二、情境导入
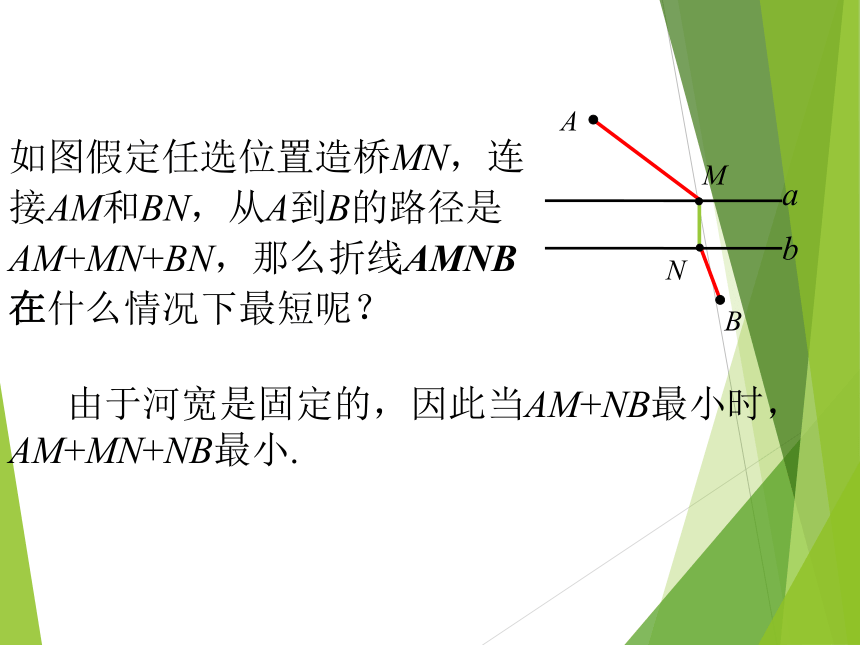
如图假定任选位置造桥MN,连接AM和BN,从A到B的路径是AM+MN+BN,那么折线AMNB在什么情况下最短呢?
a
b
B
A
M
N
由于河宽是固定的,因此当AM+NB最小时,AM+MN+NB最小.
三、设问导读
三、设问导读
l
A
B
C
a
B
A
b
M
N
四、通过类比,动手操作,自主探究
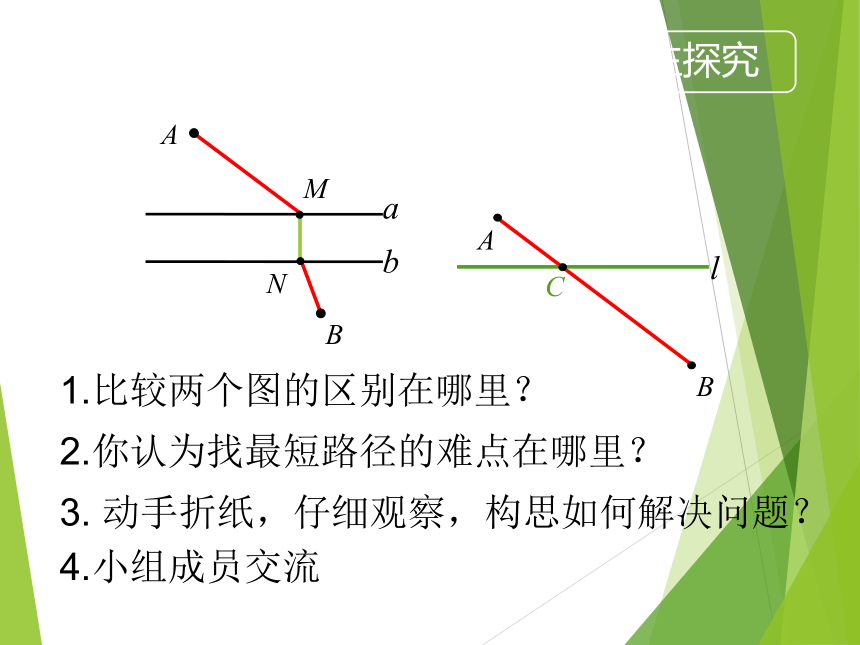
1.比较两个图的区别在哪里?
2.你认为找最短路径的难点在哪里?
3. 动手折纸,仔细观察,构思如何解决问题?
4.小组成员交流
分析:
l
A
B
C
a
B
A
b
M
N
A'
如图,如果将点A沿与河岸垂直的方向平移到点A′,使AA′等于河宽,则AA′=MN,AM=A′N,问题转化为:当点N在直线b的什么位置时,A′N+NB最小?
参考右图,利用“两点之间,线段最短”可以解决.
如图,沿垂直于河岸的方向平移A到A′,使AA′等于河宽,连接A′B交河岸于点N,在点N处造桥MN,此时路径AM+MN+BN最短.
B
A
a
b
M
N
A'
解:
五、归纳小结
抽象为数学问题
用旧知解决新知
联想旧知
解决实
际问题
l
A
B
C
转化
在解决最短路径问题时,我们通常利用轴对称、平移等变换,把较复杂的问题转化为容易解决的问题——两点之间,线段最短。从而作出最短路径的选择。
如图4,如果A、B两地之间有两条平行的河,
我们要建的桥都是与河岸垂直的.我们如何
找到这个最短的距离呢?
五、新知应用
方法1:仿照上例,可以将点A沿与河垂直的方向平移
两个河宽分别到到A1、A2,路径中两座桥的长度是固定的.
为了使路径最短,只要A2B最短.连接A2B,交河流2河岸
于N,在此处造桥MN;连接A1M,交河流1河岸于P,在此
处造桥PQ.所得路径AQPMNB最短.
方法2:如图6,将点A沿与第一条河流垂直的方向平移一
个河宽到A1,将B沿与第二条河垂直的方向平移一个河宽
到B1,连接A1B1,与两条河分别相交于N、P,在N、P两
处,分别建桥MN、PQ,所得路径AQPMNB最短
六、巩固训练
如果A、B两地之间有两条平行的河,
我们要建的桥都是与河岸垂直的.我们如何找到这个最短的距离呢?
六、巩固训练
? ?方法1:如图10,先将点A沿与河流1河岸垂直的方向平移一个河宽到A1,再沿与河流2河岸垂直的方向平移一河宽到A2,连接A2B,交河流2河岸于N,此处建桥MN;连接A1M,交河流1于P,在此处建桥PQ.所得路径AQPMNB最短.
下节课我们继续学习!再见
20.4 最短路径问题(2)
一、温故互查
1.已知:如图,A,B在直线l的两侧,在l上求一点P,使得PA+PB最小。
l
有理数:整数和分数统称为有理数
2.如图所示,要在街道旁修建一个奶站,向居民区A、B提供牛奶,奶站应建在什么地方,才能使从A、B到它的距离之和最短.
一、温故互查
3.如图,A、B是直线a同侧的两定点,定长
线段PQ在a上平行移动,问PQ移动到什么
位置时,AP+PQ+QB的长最短?
一、温故互查
(造桥选址问题)如图,A和B两地在同一条河的两岸,现要在河上造一座桥MN.桥造在何处可使从A到B的路径AMNB最短?(假定河的两岸是平行的直线,桥要与河垂直)
思考:
你能把这个问题转化
为数学问题吗?
二、情境导入
如图假定任选位置造桥MN,连接AM和BN,从A到B的路径是AM+MN+BN,那么折线AMNB在什么情况下最短呢?
a
b
B
A
M
N
由于河宽是固定的,因此当AM+NB最小时,AM+MN+NB最小.
三、设问导读
三、设问导读
l
A
B
C
a
B
A
b
M
N
四、通过类比,动手操作,自主探究
1.比较两个图的区别在哪里?
2.你认为找最短路径的难点在哪里?
3. 动手折纸,仔细观察,构思如何解决问题?
4.小组成员交流
分析:
l
A
B
C
a
B
A
b
M
N
A'
如图,如果将点A沿与河岸垂直的方向平移到点A′,使AA′等于河宽,则AA′=MN,AM=A′N,问题转化为:当点N在直线b的什么位置时,A′N+NB最小?
参考右图,利用“两点之间,线段最短”可以解决.
如图,沿垂直于河岸的方向平移A到A′,使AA′等于河宽,连接A′B交河岸于点N,在点N处造桥MN,此时路径AM+MN+BN最短.
B
A
a
b
M
N
A'
解:
五、归纳小结
抽象为数学问题
用旧知解决新知
联想旧知
解决实
际问题
l
A
B
C
转化
在解决最短路径问题时,我们通常利用轴对称、平移等变换,把较复杂的问题转化为容易解决的问题——两点之间,线段最短。从而作出最短路径的选择。
如图4,如果A、B两地之间有两条平行的河,
我们要建的桥都是与河岸垂直的.我们如何
找到这个最短的距离呢?
五、新知应用
方法1:仿照上例,可以将点A沿与河垂直的方向平移
两个河宽分别到到A1、A2,路径中两座桥的长度是固定的.
为了使路径最短,只要A2B最短.连接A2B,交河流2河岸
于N,在此处造桥MN;连接A1M,交河流1河岸于P,在此
处造桥PQ.所得路径AQPMNB最短.
方法2:如图6,将点A沿与第一条河流垂直的方向平移一
个河宽到A1,将B沿与第二条河垂直的方向平移一个河宽
到B1,连接A1B1,与两条河分别相交于N、P,在N、P两
处,分别建桥MN、PQ,所得路径AQPMNB最短
六、巩固训练
如果A、B两地之间有两条平行的河,
我们要建的桥都是与河岸垂直的.我们如何找到这个最短的距离呢?
六、巩固训练
? ?方法1:如图10,先将点A沿与河流1河岸垂直的方向平移一个河宽到A1,再沿与河流2河岸垂直的方向平移一河宽到A2,连接A2B,交河流2河岸于N,此处建桥MN;连接A1M,交河流1于P,在此处建桥PQ.所得路径AQPMNB最短.
下节课我们继续学习!再见
