人教版(五四制) 八上 20.4 最短路径问题课件 (共15张ppt)
文档属性
| 名称 | 人教版(五四制) 八上 20.4 最短路径问题课件 (共15张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 7.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-20 22:44:08 | ||
图片预览




文档简介
绿地里本没有路,走的人多了… …
看图思考:
为什么有的人会经常践踏草地呢?
比比谁快
1.下图中从A到B的4条路径中,哪条最短?
2.依据什么原理?
两点之间,线段最短
20.4最短路径问题
人教五.四学制2011课标版
知识与技能:能利用轴对称解决简单的最短路径问题。
过程与方法:体会图形的变化在解决最值问题中的作用。能利用轴对称将线段和最小值问题转化为“两点之间线段最短”问题。
情感态度与价值观:体验数学活动的探索性和创造性。
教学目标:
P
两点之间线段最短.
根据:
B
A
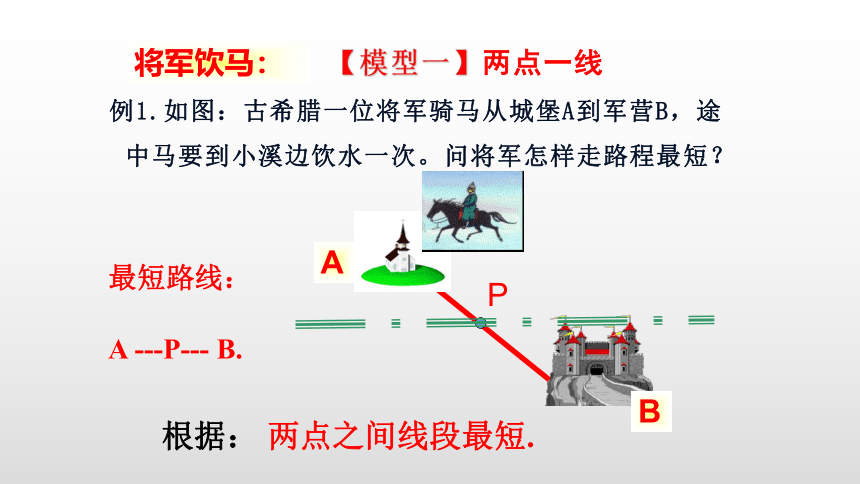
【模型一】两点一线
例1.如图:古希腊一位将军骑马从城堡A到军营B,途中马要到小溪边饮水一次。问将军怎样走路程最短?
最短路线:
将军饮马:
A ---P--- B.
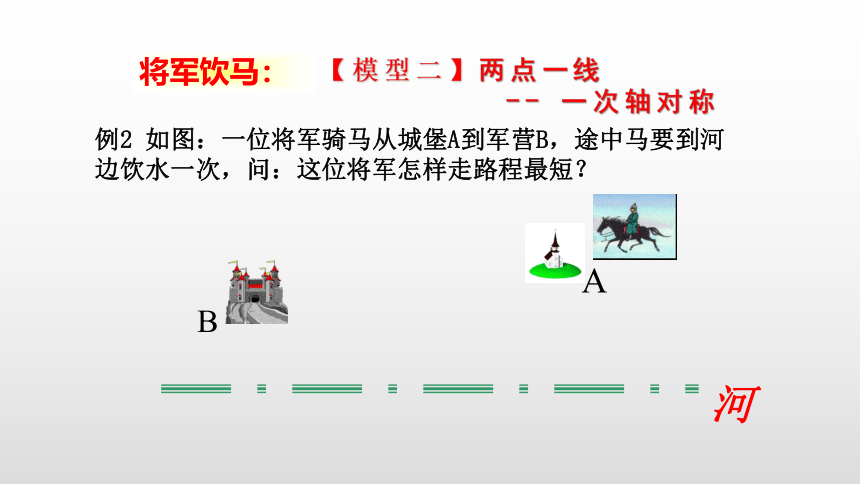
例2 如图:一位将军骑马从城堡A到军营B,途中马要到河边饮水一次,问:这位将军怎样走路程最短?
A
B
将军饮马:
【模型二】两点一线
-- 一次轴对称
河
B
A
B'
P
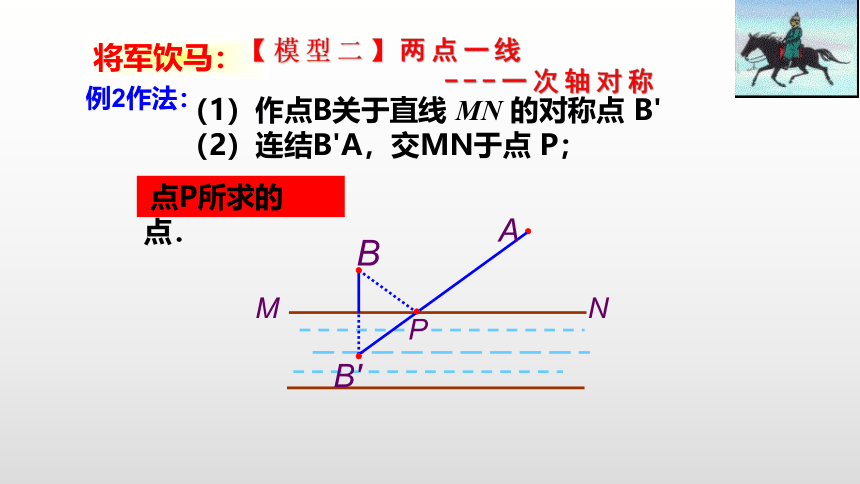
(1)作点B关于直线 MN 的对称点 B'
(2)连结B'A,交MN于点 P;
点P所求的点.
M
N
将军饮马:
例2作法:
【模型二】两点一线
---一次轴对称
注意:
1、直线l是定直线,A、B两点是直线同侧的定点。
2、定点的对称点还是定点。
3、连接定点与对称点确定动点位置。
4、求出最小值即最短距离。
变式1.在平面直角坐标系中有两点,要在y轴上找一点,使它到的A、B两点距离之和最小,现有下四种方案,其中正确的是( )
D
反思是进步的阶梯
我的收获;
我的疑惑;
面对一个新的求线段最短问题时,我们可以通过怎样的途径去研究它?
课
堂
反
思:
(1)求最短路线问题------通过几何变换找对称点。
(2)把点A,B在直线同侧的问题转化为在直线的异侧,化折线为直线。
(3)可利用“两点之间线段最短”加以解决。
课堂小结:
(2018年新疆中考数学第9题)
如图,点P是边长为1的菱形ABCD对角线AC上的一个动点,点M,N分别是AB,BC边上的中点,则MP+PN的最小值是( )
A.1/2 B.1 C.√2 D.2
巩固练习
B
如图所示,正方形ABCD的面积为12,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE的和最小,则这个最小值为______.
(2018年黄冈中考数学第13题)如图,圆柱形玻璃杯高为14cm,底面周长为32cm,在杯内壁离杯底5cm的点B处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿3cm与蜂蜜相对的点A处,则蚂蚁从外壁A处到内壁B处的最短距离为 cm(杯壁厚度不计).
能力提升
【分析】解:如图:将杯子侧面展开,作A关于EF的对称点A′,
连接A′B,则A′B即为最短距离,A′B=√(A′D?+BD?)=20(cm)。
谢谢,再见!
看图思考:
为什么有的人会经常践踏草地呢?
比比谁快
1.下图中从A到B的4条路径中,哪条最短?
2.依据什么原理?
两点之间,线段最短
20.4最短路径问题
人教五.四学制2011课标版
知识与技能:能利用轴对称解决简单的最短路径问题。
过程与方法:体会图形的变化在解决最值问题中的作用。能利用轴对称将线段和最小值问题转化为“两点之间线段最短”问题。
情感态度与价值观:体验数学活动的探索性和创造性。
教学目标:
P
两点之间线段最短.
根据:
B
A
【模型一】两点一线
例1.如图:古希腊一位将军骑马从城堡A到军营B,途中马要到小溪边饮水一次。问将军怎样走路程最短?
最短路线:
将军饮马:
A ---P--- B.
例2 如图:一位将军骑马从城堡A到军营B,途中马要到河边饮水一次,问:这位将军怎样走路程最短?
A
B
将军饮马:
【模型二】两点一线
-- 一次轴对称
河
B
A
B'
P
(1)作点B关于直线 MN 的对称点 B'
(2)连结B'A,交MN于点 P;
点P所求的点.
M
N
将军饮马:
例2作法:
【模型二】两点一线
---一次轴对称
注意:
1、直线l是定直线,A、B两点是直线同侧的定点。
2、定点的对称点还是定点。
3、连接定点与对称点确定动点位置。
4、求出最小值即最短距离。
变式1.在平面直角坐标系中有两点,要在y轴上找一点,使它到的A、B两点距离之和最小,现有下四种方案,其中正确的是( )
D
反思是进步的阶梯
我的收获;
我的疑惑;
面对一个新的求线段最短问题时,我们可以通过怎样的途径去研究它?
课
堂
反
思:
(1)求最短路线问题------通过几何变换找对称点。
(2)把点A,B在直线同侧的问题转化为在直线的异侧,化折线为直线。
(3)可利用“两点之间线段最短”加以解决。
课堂小结:
(2018年新疆中考数学第9题)
如图,点P是边长为1的菱形ABCD对角线AC上的一个动点,点M,N分别是AB,BC边上的中点,则MP+PN的最小值是( )
A.1/2 B.1 C.√2 D.2
巩固练习
B
如图所示,正方形ABCD的面积为12,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE的和最小,则这个最小值为______.
(2018年黄冈中考数学第13题)如图,圆柱形玻璃杯高为14cm,底面周长为32cm,在杯内壁离杯底5cm的点B处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿3cm与蜂蜜相对的点A处,则蚂蚁从外壁A处到内壁B处的最短距离为 cm(杯壁厚度不计).
能力提升
【分析】解:如图:将杯子侧面展开,作A关于EF的对称点A′,
连接A′B,则A′B即为最短距离,A′B=√(A′D?+BD?)=20(cm)。
谢谢,再见!
