人教版 八上 14.1.2 幂的乘方 课件 (共19张ppt)
文档属性
| 名称 | 人教版 八上 14.1.2 幂的乘方 课件 (共19张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 498.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-20 23:13:34 | ||
图片预览





文档简介
14.1.2 幂的乘方
学习目标
1.根据同底数幂的乘法法则及乘方的定义推导出幂的乘方的运算法则。
2.能利用幂的乘方的运算法则进行相应的计算和化简。
3.进一步体会利用已学知识解决新问题的化归思想。
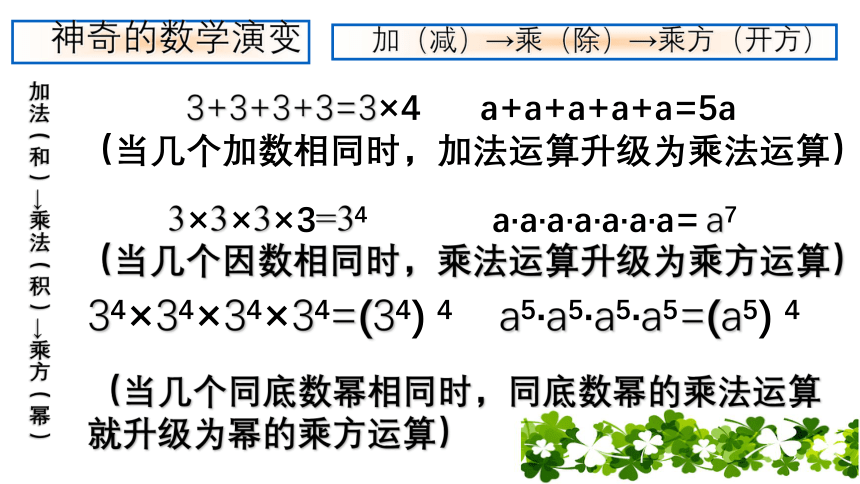
神奇的数学演变
3×3×3×3=34 a·a·a·a·a·a·a= a7
(当几个因数相同时,乘法运算升级为乘方运算)
3+3+3+3=3×4 a+a+a+a+a=5a
(当几个加数相同时,加法运算升级为乘法运算)
加法(和)→乘法(积)→乘方(幂)
34×34×34×34=(34) 4 a5·a5·a5·a5=(a5) 4
(当几个同底数幂相同时,同底数幂的乘法运算就升级为幂的乘方运算)
加(减)→乘(除)→乘方(开方)
根据乘方的意义和同底数幂的乘法法则填空:
4
4
4
2
3
5
3
3
3
3
3
=( )x( )
自我探究
你发现了什么?
猜想:
(其中m , n都是正整数)
(其中m , n都是正整数)
n个
n个
乘方的意义
同底数幂的乘法法则
乘方的意义
推导猜想:
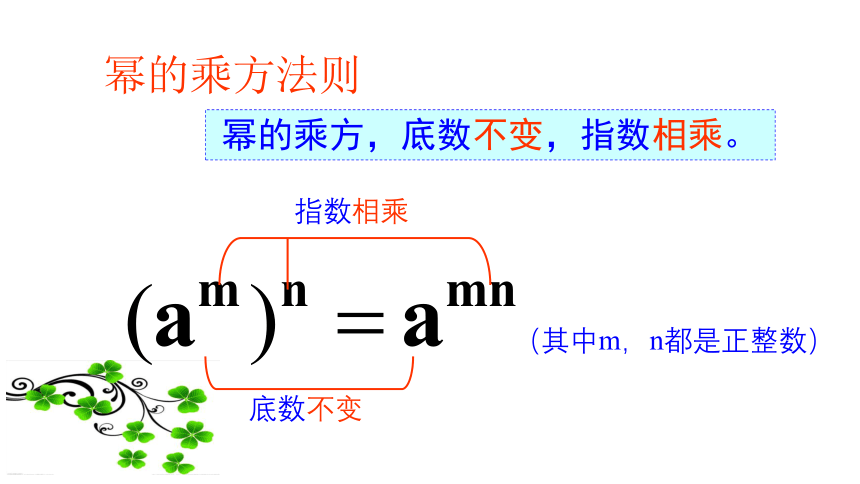
幂的乘方,底数不变,指数相乘。
幂的乘方法则
(其中m,n都是正整数)
底数不变
指数相乘
想一想:下面这道题该怎么进行计算呢?
幂的乘方的乘方
〔(am)n〕p=amnp
〔 〕4 =?
(a2)3
〔 〕4
(a2)3
=(a6)4
=a24
运算
种类
公式
运算
计算结果
底数
指数
同底数幂乘法
幂的乘方
乘法
乘方
不变
不变
指数
相加
指数
相乘
例题解析
(1)(x2)3;
(3)(a3)2-(a2)3;
(2)-(x9)8;
(4)(a2)3·a5.
思路导引:运用幂的乘方法则,运算时要先确定符号.
【规律总结】对于幂的乘方与同底数幂的
乘法的混合运算,
先算乘方,再算同底数幂的乘法;幂
的乘方与加减混合运算时,先乘方,后加
减,注意合并同类项.
计算下列各式,结果用幂的形式表示:
(2) (a3)2 ? a2
检测一:
(4) 〔(x+y)2〕3
下面的计算对吗?错的请改正:
检测二:
火眼金睛
3
面积S= .
面积S= .
体积V= .
32
32
解决问题,实际应用
检测三:
x12
=(x 4 )(3)
=(x 3 )(4 )
=(x 2 )(6)
=(x 6 )(2)
请你把 x12 写成“幂的乘方”的形式.
再探新知:
amn
=(am)n
=(an)m
1、若(x2)n=x8,则n=_______
4
2、若[(x3)m]2=x12,则m=_______
2
3、若xm?x2m=2,求x9m的值.
8
检测四:
检测五
课堂小结
1.幂的乘方的法则
(m、n都是正整数)
幂的乘方,底数不变,指数相乘.
语言叙述
符号叙述 .
2.幂的乘方的法则可以逆用.即
3.多重乘方也具有这一性质.如
(其中 m、n、p都是正整数).
公式中的a可表示一个数、字母、式子等.
作业
(3)把
化成
的形式.
(1).已知9x=310,则x的值是______。
(2).比较340与430的大小。
1.课本习题14.1第1、2题;
2.附加题:
谢 谢
已知 am=2,an=3,
求:a2m ,a3n的值;
检测五:
返回
学习目标
1.根据同底数幂的乘法法则及乘方的定义推导出幂的乘方的运算法则。
2.能利用幂的乘方的运算法则进行相应的计算和化简。
3.进一步体会利用已学知识解决新问题的化归思想。
神奇的数学演变
3×3×3×3=34 a·a·a·a·a·a·a= a7
(当几个因数相同时,乘法运算升级为乘方运算)
3+3+3+3=3×4 a+a+a+a+a=5a
(当几个加数相同时,加法运算升级为乘法运算)
加法(和)→乘法(积)→乘方(幂)
34×34×34×34=(34) 4 a5·a5·a5·a5=(a5) 4
(当几个同底数幂相同时,同底数幂的乘法运算就升级为幂的乘方运算)
加(减)→乘(除)→乘方(开方)
根据乘方的意义和同底数幂的乘法法则填空:
4
4
4
2
3
5
3
3
3
3
3
=( )x( )
自我探究
你发现了什么?
猜想:
(其中m , n都是正整数)
(其中m , n都是正整数)
n个
n个
乘方的意义
同底数幂的乘法法则
乘方的意义
推导猜想:
幂的乘方,底数不变,指数相乘。
幂的乘方法则
(其中m,n都是正整数)
底数不变
指数相乘
想一想:下面这道题该怎么进行计算呢?
幂的乘方的乘方
〔(am)n〕p=amnp
〔 〕4 =?
(a2)3
〔 〕4
(a2)3
=(a6)4
=a24
运算
种类
公式
运算
计算结果
底数
指数
同底数幂乘法
幂的乘方
乘法
乘方
不变
不变
指数
相加
指数
相乘
例题解析
(1)(x2)3;
(3)(a3)2-(a2)3;
(2)-(x9)8;
(4)(a2)3·a5.
思路导引:运用幂的乘方法则,运算时要先确定符号.
【规律总结】对于幂的乘方与同底数幂的
乘法的混合运算,
先算乘方,再算同底数幂的乘法;幂
的乘方与加减混合运算时,先乘方,后加
减,注意合并同类项.
计算下列各式,结果用幂的形式表示:
(2) (a3)2 ? a2
检测一:
(4) 〔(x+y)2〕3
下面的计算对吗?错的请改正:
检测二:
火眼金睛
3
面积S= .
面积S= .
体积V= .
32
32
解决问题,实际应用
检测三:
x12
=(x 4 )(3)
=(x 3 )(4 )
=(x 2 )(6)
=(x 6 )(2)
请你把 x12 写成“幂的乘方”的形式.
再探新知:
amn
=(am)n
=(an)m
1、若(x2)n=x8,则n=_______
4
2、若[(x3)m]2=x12,则m=_______
2
3、若xm?x2m=2,求x9m的值.
8
检测四:
检测五
课堂小结
1.幂的乘方的法则
(m、n都是正整数)
幂的乘方,底数不变,指数相乘.
语言叙述
符号叙述 .
2.幂的乘方的法则可以逆用.即
3.多重乘方也具有这一性质.如
(其中 m、n、p都是正整数).
公式中的a可表示一个数、字母、式子等.
作业
(3)把
化成
的形式.
(1).已知9x=310,则x的值是______。
(2).比较340与430的大小。
1.课本习题14.1第1、2题;
2.附加题:
谢 谢
已知 am=2,an=3,
求:a2m ,a3n的值;
检测五:
返回
