京改版八年级全册 物理 课件 第六章 功和能 复习课件(63张ppt)
文档属性
| 名称 | 京改版八年级全册 物理 课件 第六章 功和能 复习课件(63张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 1007.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-08-21 21:11:58 | ||
图片预览









文档简介
第六章 功和能
复习课件
一、机械功的含义
1.定义:
如果作用于物体的恒力大小为F,该物体沿力的方向运动,经过位移s,则F与s的乘积叫做机械功。
2.做功的两个因素:
(1)作用在物体上的力。
(2)物体在这个力的方向上移动的距离。
6.1功
C
例1.用水平恒力F作用于质量为M的物体,使之在光滑的水平面上沿力的方向移动距离S,恒力做功为W1,再用该恒力作用于质量为m(mA.W1>W2 B.W1本题说明了一个力所做的功,只由力和在力的方向上发生的位移决定,跟物体是否还受到其它力作用,以及物体的运动情况均无关。
10m
50N
100N
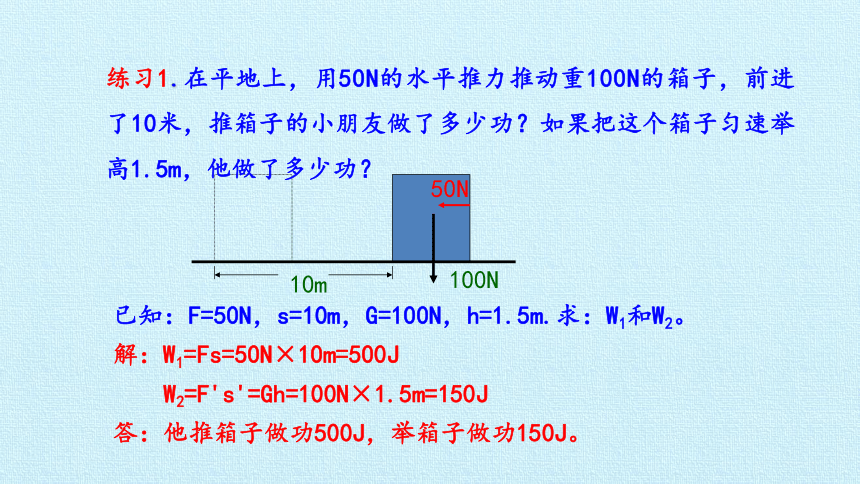
练习1.在平地上,用50N的水平推力推动重100N的箱子,前进了10米,推箱子的小朋友做了多少功?如果把这个箱子匀速举高1.5m,他做了多少功?
已知:F=50N,s=10m,G=100N,h=1.5m.求:W1和W2。
解:W1=Fs=50N×10m=500J
W2=F's'=Gh=100N×1.5m=150J
答:他推箱子做功500J,举箱子做功150J。
练习2.用200N的恒力,在粗糙程度不同的水平路面上,沿水平方向分别拉重500N和800N的两辆小车,小车匀速前进4m,则( )
A.拉重车做的功多
B.拉轻车做的功多
C.拉两辆车做的功一样多
D.无法确定
C
二、机械功的计算
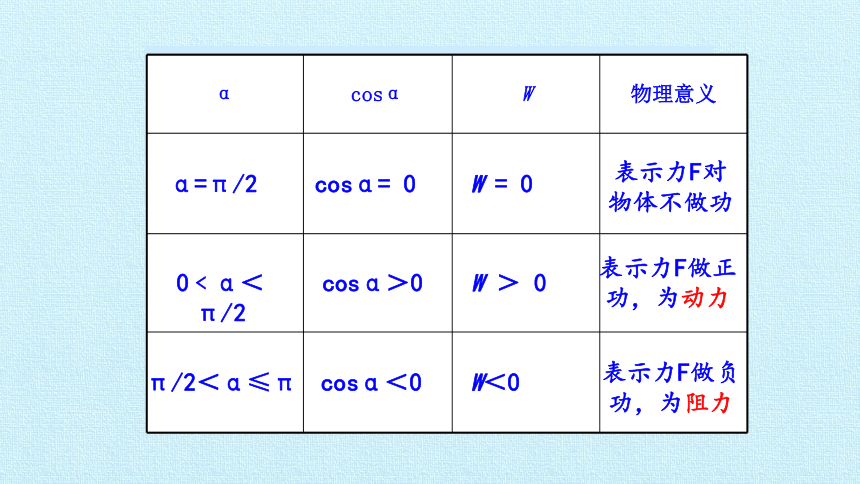
1.正功和负功
α
cosα
W
物理意义
α=π/2
0﹤α<π/2
π/2<α≤π
cosα= 0
cosα>0
cosα<0
W = 0
W > 0
W<0
表示力F对物体不做功
表示力F做正功,为动力
表示力F做负功,为阻力
方法一:
先求出各分力的功,再利用合外力的功等于物体各力功的代数和求出W合=W1+W2+W3+…
实际都用此法求。
总功的求法
方法二:
先求出合外力F合,再利用W合=F合s cosα求出合外力的功
结论:几个力对一个物体做功的代数和,等于这几个力的合力对这个物体所做的功。
例2.一位质量为m=60kg的滑雪运动员从高为h=10m的斜坡上自由下滑。如果运动员在下滑过程中所受到的阻力F=50N,斜坡的倾角θ=30°,运动员滑至坡底的过程中,所受的几个力所做的功各是多少?这些力所做的总功是多少?
解:滑雪运动员受到重力、支持力和阻力,运动员的位移为:s=h/sin30°=20m,方向沿斜坡向下。
重力做功:WG=mgscos60°
=60×10×20×1/2J=6.0×103J
弹力做功:WN=FNscos90°=0
阻力做功:WF=Fscos180°=-50×20J=-1.0×103J
合力做功:W总=WG+WN+WF=5.0×103J
θ
v
F
FN
G
练习3.用起重机把重为2.0×104 N的物体匀速地提高了5m,钢绳的拉力做了多少功?重力做了多少功?物体克服重力做了多少功?这些力所做的总功是多少 ?
解:重物被匀速提升时,合力为0,钢绳对重物的拉力的大小等于重物所受的重力,即F=G=2×104N
钢绳拉力所做的功为
W1=Fscosθ=2×104×5J=1×105J
重力做的功为
W2=Gscosθ=-2×104×5J=-1×105J
W克=∣W2∣=1×105J ,
W合=W1+W2=1×105-1×105=0
一、功率的含义
1.功率的定义:功跟完成这些功所用时间的比值,叫做功率。
2.功率的公式:P=
3.功率的物理意义:表示物体做功快慢的物理量。
6.2功率
功率是标量,表示做功过程中能量转化的快慢。
功率的单位:在国际单位制中,功率的单位是瓦特,简称瓦,符号是W,
1W=1J/s
技术上常用千瓦(kW)作为功率的单位,
1kW=1000W。
例1.关于功率,下列说法中正确的是( )
A.功率是说明做功多少的物理量
B.功率是说明力做功快慢的物理量
C.做功时间越长,功率一定越小
D.力做功越多,功率一定越大
B
1.某人用同一水平力F先后两次拉同一物体,第一次使此物体沿光滑水平面前进s距离,第二次使此物体沿粗糙水平面也前进s距离,若先后两次拉力做的功为W1和W2,拉力做功的功率是P1和P2,则( )
A.W1=W2,P1=P2 B.W1=W2,P1>P2
C.W1>W2,P1>P2 D.W1>W2,P1=P2
B
2.一台抽水机每秒能把30kg的水抽到10m高的水塔上,不计额外功的损失,这台抽水机输出的功率是多大?如果保持这一输出功率,半小时内能做多少功?
解:m=30 kg h=10 m t=1800 s
由功W=mgh 得W=30×10×10J=3×103 J
∴这台抽水机的输出功率为
由P=W/t
得 P=3×103 /1 W=3×103 W
它半小时能做功
W=Pt=3×103×1800J=5.4×106J
二、功率与力、速度的关系
F
v
水平力F推物体,让物体以速度v做匀速直线运动,力F对物体做功的功率:
W=FS
P=
v=S/t
P=Fv
F与v成任意角度θ,则功率与力、速度的关系为:
W=Fscosθ
P=W/t
v=s/t
P=Fvcosθ
三、额定功率和实际功率
1.额定功率:是指机器长时间工作时的最大允许功率,也就是机器铭牌上的标称值,这个功率叫做额定功率。
2.实际功率:是指机器在工作中实际输出的功率。
3.机器不一定在额定功率下工作,机器正常工作时实际功率总是小于或等于额定功率,机器只能在短暂时间内实际功率略大于额定功率,但不允许长时间超过额定功率。
说明:在日常生活中,我们经常说某台机器的功率,或某物体做功的功率,实际上是指某个力对物体做功的功率。例如:汽车的功率就是汽车牵引力的功率,起重机吊起货物的功率就是钢绳拉力的功率。
1.平均功率:
物体在一段时间内做功的功率的平均值称为平均功率。描述在一段时间内做功的平均快慢 ,通常用P=W/t来表示。
2.瞬时功率:
物体在某一时刻的功率叫做瞬时功率。表示在某一时刻做功的快慢,用P=Fv表述,v是瞬时速度。
四、平均功率和瞬时功率
例2.一物体自某一高度处做自由落体运动,经5s落地,其质量为m=2kg,问:
(1)在5s内重力的平均功率为多大?
(2)在4s末,重力的瞬时功率为多少?
解析:(1)物体做自由落体运动,由h= gt2
得h= ×10×52m=125m
根据做功公式 W=Fs 得W=mgh=2500J
由P=W/t 得平均功率P=500W
(2)由v=gt 得4s末的速度 v=40m/s
由瞬时功率P=Fv得P=mgv=20×40W=800W
例3.某型号汽车发动机的额定功率为60kW,在水平路面上行驶时受到的阻力是1800N,求发动机在额定功率下汽车匀速行驶的速度。在同样的阻力下,如果行驶速度只有54km/h,发动机输出的实际功率是多少?
解:知P= 6×104W,F阻=1800N,v'= 54km/h=15m/s, 汽车匀速行驶时,有F牵=F阻
(1)由公式 P=Fv
得v=P/F阻=33.3m/s=120km/h
(2)当以较低的速度行驶时,v'=54km/h=15m/s
∴P'=Fv'=27kW
五、汽车两种启动方式的讨论
1.功率P恒定
由P=Fv可知,v增大,F减小,由F-f=ma知,a减小,v增加的慢了但仍继续增加,F减小,a进一步减小,当a=0时,即F=f时,速度达到最大vm
2.加速度a恒定
由F-f=ma知,F恒定,根据P=Fv,v逐渐增大,则P逐渐增大,当达到额定功率时,P不能再增大,匀加速阶段结束。再往后,v继续增大,P不变,F减小,a开始减小,直到a=0时,F=f,速度达到最大vm
例4.按额定功率行驶的汽车,所受地面的阻力保持不变,则( )
A.汽车加速行驶时,牵引力不变,速度增大
B.汽车可以做匀加速运动
C.汽车加速行驶时,加速度逐渐减小,速度逐渐增大
D.汽车达到最大速度时,所受合力为零
CD
3.下列关于汽车运动的论述,不正确的是( )
A.汽车以额定功率启动后做变加速运动,速度、加速度均逐渐增大
B.汽车以额定功率启动后做变加速运动,速度逐渐增大;加速度逐渐减小,加速度为0时,速度最大
C.汽车匀速行驶时最大允许速度受发动机额定功率限制,要提高最大允许速度,必须增大发动机的额定功率
D.汽车在水平路面上以额定功率P行驶,则当牵引力F与阻力f平衡时,汽车的最大速度vm=P/f
A
4.额定功率为80kW的汽车,在水平长直公路上行驶时最大速度可达20m/s,汽车质量为2×103kg。如果汽车从静止开始做匀加速直线运动,加速度可达2m/s2。设运动过程中阻力大小不变,试求:
(1)汽车运动时所受阻力f;
(2)汽车匀加速运动过程可持续的时间t';
(3)汽车启动后,发动机在第三秒末的瞬时功率P3。
解:(1)当F=f时,a=0 由P=Fv=fvm
所以f=P额 /vm =4 ×103 N
(2)根据牛顿运动定律F-f=ma
得F=f+ma=8 ×103 N
设汽车刚达到额定功率时速度为v'm
汽车匀加速运动的时间为t′
由P额=Fv'm 得 v'm =10m/s
V'm=at' t'=5s
(3)汽车第3s末仍在做匀加速运动
则v3=at3=2×3m/s=6m/s
P3=Fv3=4.8 ×104W
6.3功的原理
一、机械的三种功
使用任何机械都不能省功
功的原理
机械的三种功
G
F
要提升G,同时必须将本滑轮也提升。嘿,你要克服本滑轮重力和摩擦而额外做功,否则你不能完成任务。本功无利用价值而又不得不做,是额外功。
提升本G是目的,有利用价值,是有用功。
要实现目的,完成有用功,必须施加本动力F对滑轮做功,是总功。
有用功:我们把必需做的那部分功叫做有用功(克服有用阻力所做的功)。
额外功:把虽然不需要,但又不得不做的那部分功叫做额外功(克服额外阻力所做的功)
总功:有用功与额外功的总和叫总功(动力所做的功)。
动力对机械所做的功
有两个
效果
为达到目标,克服机械本身重力和摩擦,对人们无利用价值而又不得不做的功
克服机械自
身部件(如
动滑轮、绳
子)的重力
和摩擦等而
做的功
实现目的,有利用价值的功
实现目的
而做功
根据功的原理
二、机械效率
G
F
我们总希望,有用功占总功中的份额越大越好。
1.定义:有用功跟总功的比值,叫做机械效率。
正确理解机械效率,关键是明确三种功。
忽略我的重力和摩擦,我的机械效率是等于1;其它任何情况,我的机械效率都小于1。
精选例题
G
F
G
F
1.使用下面的两个滑轮组,提升相同的重物,提升相同的高度,哪个机械效率大?
动滑轮个数较少,自重轻,绳子股数少,摩擦也小,额外功较少
动滑轮个数较多,绳子股数多,额外功较多
将相同重物提升相同
高度,做有用功相同
2.使用下面的滑轮组,用拉力F匀速拉动重物水平移动的距离为L,有用功是多少?机械效率等于什么?
F
G
f
G
L
本题使用滑轮组的任务目的是拉动G水平移动L,所以机械克服G和地面的摩擦力做功是有用功。
使用滑轮组拉动G,必须施加动力F
根据机械效率的定义
3.某人用如图所示的滑轮组提升2000牛的重物,用的拉力是800牛,绳子自由端被拉下4米。(1)这个人做的总功是多少焦?(2)有用功是多少焦?(3)额外功是多少焦?(4)这个滑轮组的机械效率是多少?
已知:G=2000牛 F=800米 S=4米 n=4
求:
F
G
G
F
1.物体重为60牛,拉力F向上拉过3米。若滑轮本身重及摩擦不计,所用拉力F为——牛,拉力F做功——焦。
30
90
巩固练习
G
2.用滑轮组提升=400牛的重物,若不计滑轮重和摩擦,则:
(1)绳子自由端所用力F= ——牛。
(2)若拉力做功800焦,则绳子自由端移动——米,重物上升——米。
200
4
2
A
B
C
l
h
G
F
3.沿着光滑的斜面用力F将重为=60牛重物推上斜面,如l=4.5米,h=1.5米,那么F=——牛。推力做功——焦耳。
20
90
4.如图,用相同时间沿斜面长度不同,高度相同的光滑斜面,将两个物体由底端匀速拉到顶端,设拉力分别为F1、F2,功率分别为P1、P2。则比较F1 F2 ;P1 P2。
=
F1
F2
>
5.将一个重为100牛的物体沿斜面上拉,拉力的大小为50牛,若斜面光滑,则斜面的高度与长度之比___________,若斜面的效率为80%,则斜面的高度与长度之比为_________。
1:2
2:5
2.物体能够做的功越多,它具有的能就越大。
1.物体能够对外做功,我们就说这个物体具有能量,简称能。
3.能的单位:焦(J)
一、能
6.4机械能
动能
物体由于 而具有的能量
运动
重力势能
物体由于 而具有的能量
被举高
弹性形变
弹性势能
物体由于________而具有的能量
势能
①流水推竹排前进
④风吹帆船前进
⑤举高的重锤
②高山上的大石块
⑥
③
控制不变量
自变量
因变量
动能大小
速度
物体的质量
二、影响动能大小的因素
1.速度
速度
质量
滑块移动的距离
动能的大小
小
相同
质量
较大
大
动能大小与物体的速度的关系
较大
大
小
长
较长
短
结论:物体的质量一定,速度越大,具有的动能就越大。
2.质量
物体的质量
控制不变量
自变量
因变量
动能的大小
速度
质量
速度
滑块移动的距离
动能的大小
小
相同
速度
较大
大
动能大小与物体的质量的关系
较长
长
小
较大
大
结论:物体的速度一定,质量越大,具有的动能就越大。
短
小结:动能的大小与物体的质量和物体运动的速度有关。
物体的质量
控制不变量
自变量
因变量
重力势能
的大小
被举的高度
结论:物体的质量一定,物体被举高的
高度越大,具有的重力势能就越大。
三、影响重力势能大小的因素
1.高度
2.质量
物体的质量
控制不变量
自变量
因变量
重力势能
的大小
被举的高度
结论:物体被举高的高度一定,质量越大,具有的重力势能就越大。
小结:重力势能的大小与物体的质量和被举的高度有关。
具有弹性的物体由于发生弹性形变具有的能,叫弹性势能。
四、影响弹性势能大小的因素
物体的弹性形变越大,物体的弹性势能越大。
动能和势能统称为机械能。
滚摆
上升过程:
下降过程:
动能减小,重力势能增加。
动能增加,重力势能减小。
动能 重力势能
转化
重力势能 动能
转化
滚摆
五、动能和势能相互转化
结论:动能和势能可以相互转化的。
在只有动能和势能相互转化的过程中,机械能的总量保持不变。(即:机械能守恒)
动能
势能
重力势能
弹性势能
机械能
小结
质量(m)
速度(V)
质量(m)
被举高的
高度(h)
物体的弹性形变
能量:物体能够对外做功
转化
习题检测
1.你能说出这些物体具有什么形式的能吗?
(1)在水平公路上行驶的汽车具有____;
(2)被拉弯的弓具有_________;
(3)被举高的重锤具有________。
动能
弹性势能
重力势能
2.滑雪运动员脚踩滑雪板从高处滑下,在此过程中,运动员的动能__ _,势能_ _。
(填“变大”或“变小”)
变大
变小
3.一架飞机在灾区上方水平匀速飞行,并不断向灾区空投救灾物资,则飞机在这个过程中,动能_____,势能____。(填“变大”或“变小”)
变小
变小
4.下列哪个物体没有弹性势能( )
A.压缩的弹簧 B.踏上运动员的跳板
C.变瘪的橡皮泥 D.躺着人的弹簧床
C
谢 谢
复习课件
一、机械功的含义
1.定义:
如果作用于物体的恒力大小为F,该物体沿力的方向运动,经过位移s,则F与s的乘积叫做机械功。
2.做功的两个因素:
(1)作用在物体上的力。
(2)物体在这个力的方向上移动的距离。
6.1功
C
例1.用水平恒力F作用于质量为M的物体,使之在光滑的水平面上沿力的方向移动距离S,恒力做功为W1,再用该恒力作用于质量为m(m
10m
50N
100N
练习1.在平地上,用50N的水平推力推动重100N的箱子,前进了10米,推箱子的小朋友做了多少功?如果把这个箱子匀速举高1.5m,他做了多少功?
已知:F=50N,s=10m,G=100N,h=1.5m.求:W1和W2。
解:W1=Fs=50N×10m=500J
W2=F's'=Gh=100N×1.5m=150J
答:他推箱子做功500J,举箱子做功150J。
练习2.用200N的恒力,在粗糙程度不同的水平路面上,沿水平方向分别拉重500N和800N的两辆小车,小车匀速前进4m,则( )
A.拉重车做的功多
B.拉轻车做的功多
C.拉两辆车做的功一样多
D.无法确定
C
二、机械功的计算
1.正功和负功
α
cosα
W
物理意义
α=π/2
0﹤α<π/2
π/2<α≤π
cosα= 0
cosα>0
cosα<0
W = 0
W > 0
W<0
表示力F对物体不做功
表示力F做正功,为动力
表示力F做负功,为阻力
方法一:
先求出各分力的功,再利用合外力的功等于物体各力功的代数和求出W合=W1+W2+W3+…
实际都用此法求。
总功的求法
方法二:
先求出合外力F合,再利用W合=F合s cosα求出合外力的功
结论:几个力对一个物体做功的代数和,等于这几个力的合力对这个物体所做的功。
例2.一位质量为m=60kg的滑雪运动员从高为h=10m的斜坡上自由下滑。如果运动员在下滑过程中所受到的阻力F=50N,斜坡的倾角θ=30°,运动员滑至坡底的过程中,所受的几个力所做的功各是多少?这些力所做的总功是多少?
解:滑雪运动员受到重力、支持力和阻力,运动员的位移为:s=h/sin30°=20m,方向沿斜坡向下。
重力做功:WG=mgscos60°
=60×10×20×1/2J=6.0×103J
弹力做功:WN=FNscos90°=0
阻力做功:WF=Fscos180°=-50×20J=-1.0×103J
合力做功:W总=WG+WN+WF=5.0×103J
θ
v
F
FN
G
练习3.用起重机把重为2.0×104 N的物体匀速地提高了5m,钢绳的拉力做了多少功?重力做了多少功?物体克服重力做了多少功?这些力所做的总功是多少 ?
解:重物被匀速提升时,合力为0,钢绳对重物的拉力的大小等于重物所受的重力,即F=G=2×104N
钢绳拉力所做的功为
W1=Fscosθ=2×104×5J=1×105J
重力做的功为
W2=Gscosθ=-2×104×5J=-1×105J
W克=∣W2∣=1×105J ,
W合=W1+W2=1×105-1×105=0
一、功率的含义
1.功率的定义:功跟完成这些功所用时间的比值,叫做功率。
2.功率的公式:P=
3.功率的物理意义:表示物体做功快慢的物理量。
6.2功率
功率是标量,表示做功过程中能量转化的快慢。
功率的单位:在国际单位制中,功率的单位是瓦特,简称瓦,符号是W,
1W=1J/s
技术上常用千瓦(kW)作为功率的单位,
1kW=1000W。
例1.关于功率,下列说法中正确的是( )
A.功率是说明做功多少的物理量
B.功率是说明力做功快慢的物理量
C.做功时间越长,功率一定越小
D.力做功越多,功率一定越大
B
1.某人用同一水平力F先后两次拉同一物体,第一次使此物体沿光滑水平面前进s距离,第二次使此物体沿粗糙水平面也前进s距离,若先后两次拉力做的功为W1和W2,拉力做功的功率是P1和P2,则( )
A.W1=W2,P1=P2 B.W1=W2,P1>P2
C.W1>W2,P1>P2 D.W1>W2,P1=P2
B
2.一台抽水机每秒能把30kg的水抽到10m高的水塔上,不计额外功的损失,这台抽水机输出的功率是多大?如果保持这一输出功率,半小时内能做多少功?
解:m=30 kg h=10 m t=1800 s
由功W=mgh 得W=30×10×10J=3×103 J
∴这台抽水机的输出功率为
由P=W/t
得 P=3×103 /1 W=3×103 W
它半小时能做功
W=Pt=3×103×1800J=5.4×106J
二、功率与力、速度的关系
F
v
水平力F推物体,让物体以速度v做匀速直线运动,力F对物体做功的功率:
W=FS
P=
v=S/t
P=Fv
F与v成任意角度θ,则功率与力、速度的关系为:
W=Fscosθ
P=W/t
v=s/t
P=Fvcosθ
三、额定功率和实际功率
1.额定功率:是指机器长时间工作时的最大允许功率,也就是机器铭牌上的标称值,这个功率叫做额定功率。
2.实际功率:是指机器在工作中实际输出的功率。
3.机器不一定在额定功率下工作,机器正常工作时实际功率总是小于或等于额定功率,机器只能在短暂时间内实际功率略大于额定功率,但不允许长时间超过额定功率。
说明:在日常生活中,我们经常说某台机器的功率,或某物体做功的功率,实际上是指某个力对物体做功的功率。例如:汽车的功率就是汽车牵引力的功率,起重机吊起货物的功率就是钢绳拉力的功率。
1.平均功率:
物体在一段时间内做功的功率的平均值称为平均功率。描述在一段时间内做功的平均快慢 ,通常用P=W/t来表示。
2.瞬时功率:
物体在某一时刻的功率叫做瞬时功率。表示在某一时刻做功的快慢,用P=Fv表述,v是瞬时速度。
四、平均功率和瞬时功率
例2.一物体自某一高度处做自由落体运动,经5s落地,其质量为m=2kg,问:
(1)在5s内重力的平均功率为多大?
(2)在4s末,重力的瞬时功率为多少?
解析:(1)物体做自由落体运动,由h= gt2
得h= ×10×52m=125m
根据做功公式 W=Fs 得W=mgh=2500J
由P=W/t 得平均功率P=500W
(2)由v=gt 得4s末的速度 v=40m/s
由瞬时功率P=Fv得P=mgv=20×40W=800W
例3.某型号汽车发动机的额定功率为60kW,在水平路面上行驶时受到的阻力是1800N,求发动机在额定功率下汽车匀速行驶的速度。在同样的阻力下,如果行驶速度只有54km/h,发动机输出的实际功率是多少?
解:知P= 6×104W,F阻=1800N,v'= 54km/h=15m/s, 汽车匀速行驶时,有F牵=F阻
(1)由公式 P=Fv
得v=P/F阻=33.3m/s=120km/h
(2)当以较低的速度行驶时,v'=54km/h=15m/s
∴P'=Fv'=27kW
五、汽车两种启动方式的讨论
1.功率P恒定
由P=Fv可知,v增大,F减小,由F-f=ma知,a减小,v增加的慢了但仍继续增加,F减小,a进一步减小,当a=0时,即F=f时,速度达到最大vm
2.加速度a恒定
由F-f=ma知,F恒定,根据P=Fv,v逐渐增大,则P逐渐增大,当达到额定功率时,P不能再增大,匀加速阶段结束。再往后,v继续增大,P不变,F减小,a开始减小,直到a=0时,F=f,速度达到最大vm
例4.按额定功率行驶的汽车,所受地面的阻力保持不变,则( )
A.汽车加速行驶时,牵引力不变,速度增大
B.汽车可以做匀加速运动
C.汽车加速行驶时,加速度逐渐减小,速度逐渐增大
D.汽车达到最大速度时,所受合力为零
CD
3.下列关于汽车运动的论述,不正确的是( )
A.汽车以额定功率启动后做变加速运动,速度、加速度均逐渐增大
B.汽车以额定功率启动后做变加速运动,速度逐渐增大;加速度逐渐减小,加速度为0时,速度最大
C.汽车匀速行驶时最大允许速度受发动机额定功率限制,要提高最大允许速度,必须增大发动机的额定功率
D.汽车在水平路面上以额定功率P行驶,则当牵引力F与阻力f平衡时,汽车的最大速度vm=P/f
A
4.额定功率为80kW的汽车,在水平长直公路上行驶时最大速度可达20m/s,汽车质量为2×103kg。如果汽车从静止开始做匀加速直线运动,加速度可达2m/s2。设运动过程中阻力大小不变,试求:
(1)汽车运动时所受阻力f;
(2)汽车匀加速运动过程可持续的时间t';
(3)汽车启动后,发动机在第三秒末的瞬时功率P3。
解:(1)当F=f时,a=0 由P=Fv=fvm
所以f=P额 /vm =4 ×103 N
(2)根据牛顿运动定律F-f=ma
得F=f+ma=8 ×103 N
设汽车刚达到额定功率时速度为v'm
汽车匀加速运动的时间为t′
由P额=Fv'm 得 v'm =10m/s
V'm=at' t'=5s
(3)汽车第3s末仍在做匀加速运动
则v3=at3=2×3m/s=6m/s
P3=Fv3=4.8 ×104W
6.3功的原理
一、机械的三种功
使用任何机械都不能省功
功的原理
机械的三种功
G
F
要提升G,同时必须将本滑轮也提升。嘿,你要克服本滑轮重力和摩擦而额外做功,否则你不能完成任务。本功无利用价值而又不得不做,是额外功。
提升本G是目的,有利用价值,是有用功。
要实现目的,完成有用功,必须施加本动力F对滑轮做功,是总功。
有用功:我们把必需做的那部分功叫做有用功(克服有用阻力所做的功)。
额外功:把虽然不需要,但又不得不做的那部分功叫做额外功(克服额外阻力所做的功)
总功:有用功与额外功的总和叫总功(动力所做的功)。
动力对机械所做的功
有两个
效果
为达到目标,克服机械本身重力和摩擦,对人们无利用价值而又不得不做的功
克服机械自
身部件(如
动滑轮、绳
子)的重力
和摩擦等而
做的功
实现目的,有利用价值的功
实现目的
而做功
根据功的原理
二、机械效率
G
F
我们总希望,有用功占总功中的份额越大越好。
1.定义:有用功跟总功的比值,叫做机械效率。
正确理解机械效率,关键是明确三种功。
忽略我的重力和摩擦,我的机械效率是等于1;其它任何情况,我的机械效率都小于1。
精选例题
G
F
G
F
1.使用下面的两个滑轮组,提升相同的重物,提升相同的高度,哪个机械效率大?
动滑轮个数较少,自重轻,绳子股数少,摩擦也小,额外功较少
动滑轮个数较多,绳子股数多,额外功较多
将相同重物提升相同
高度,做有用功相同
2.使用下面的滑轮组,用拉力F匀速拉动重物水平移动的距离为L,有用功是多少?机械效率等于什么?
F
G
f
G
L
本题使用滑轮组的任务目的是拉动G水平移动L,所以机械克服G和地面的摩擦力做功是有用功。
使用滑轮组拉动G,必须施加动力F
根据机械效率的定义
3.某人用如图所示的滑轮组提升2000牛的重物,用的拉力是800牛,绳子自由端被拉下4米。(1)这个人做的总功是多少焦?(2)有用功是多少焦?(3)额外功是多少焦?(4)这个滑轮组的机械效率是多少?
已知:G=2000牛 F=800米 S=4米 n=4
求:
F
G
G
F
1.物体重为60牛,拉力F向上拉过3米。若滑轮本身重及摩擦不计,所用拉力F为——牛,拉力F做功——焦。
30
90
巩固练习
G
2.用滑轮组提升=400牛的重物,若不计滑轮重和摩擦,则:
(1)绳子自由端所用力F= ——牛。
(2)若拉力做功800焦,则绳子自由端移动——米,重物上升——米。
200
4
2
A
B
C
l
h
G
F
3.沿着光滑的斜面用力F将重为=60牛重物推上斜面,如l=4.5米,h=1.5米,那么F=——牛。推力做功——焦耳。
20
90
4.如图,用相同时间沿斜面长度不同,高度相同的光滑斜面,将两个物体由底端匀速拉到顶端,设拉力分别为F1、F2,功率分别为P1、P2。则比较F1 F2 ;P1 P2。
=
F1
F2
>
5.将一个重为100牛的物体沿斜面上拉,拉力的大小为50牛,若斜面光滑,则斜面的高度与长度之比___________,若斜面的效率为80%,则斜面的高度与长度之比为_________。
1:2
2:5
2.物体能够做的功越多,它具有的能就越大。
1.物体能够对外做功,我们就说这个物体具有能量,简称能。
3.能的单位:焦(J)
一、能
6.4机械能
动能
物体由于 而具有的能量
运动
重力势能
物体由于 而具有的能量
被举高
弹性形变
弹性势能
物体由于________而具有的能量
势能
①流水推竹排前进
④风吹帆船前进
⑤举高的重锤
②高山上的大石块
⑥
③
控制不变量
自变量
因变量
动能大小
速度
物体的质量
二、影响动能大小的因素
1.速度
速度
质量
滑块移动的距离
动能的大小
小
相同
质量
较大
大
动能大小与物体的速度的关系
较大
大
小
长
较长
短
结论:物体的质量一定,速度越大,具有的动能就越大。
2.质量
物体的质量
控制不变量
自变量
因变量
动能的大小
速度
质量
速度
滑块移动的距离
动能的大小
小
相同
速度
较大
大
动能大小与物体的质量的关系
较长
长
小
较大
大
结论:物体的速度一定,质量越大,具有的动能就越大。
短
小结:动能的大小与物体的质量和物体运动的速度有关。
物体的质量
控制不变量
自变量
因变量
重力势能
的大小
被举的高度
结论:物体的质量一定,物体被举高的
高度越大,具有的重力势能就越大。
三、影响重力势能大小的因素
1.高度
2.质量
物体的质量
控制不变量
自变量
因变量
重力势能
的大小
被举的高度
结论:物体被举高的高度一定,质量越大,具有的重力势能就越大。
小结:重力势能的大小与物体的质量和被举的高度有关。
具有弹性的物体由于发生弹性形变具有的能,叫弹性势能。
四、影响弹性势能大小的因素
物体的弹性形变越大,物体的弹性势能越大。
动能和势能统称为机械能。
滚摆
上升过程:
下降过程:
动能减小,重力势能增加。
动能增加,重力势能减小。
动能 重力势能
转化
重力势能 动能
转化
滚摆
五、动能和势能相互转化
结论:动能和势能可以相互转化的。
在只有动能和势能相互转化的过程中,机械能的总量保持不变。(即:机械能守恒)
动能
势能
重力势能
弹性势能
机械能
小结
质量(m)
速度(V)
质量(m)
被举高的
高度(h)
物体的弹性形变
能量:物体能够对外做功
转化
习题检测
1.你能说出这些物体具有什么形式的能吗?
(1)在水平公路上行驶的汽车具有____;
(2)被拉弯的弓具有_________;
(3)被举高的重锤具有________。
动能
弹性势能
重力势能
2.滑雪运动员脚踩滑雪板从高处滑下,在此过程中,运动员的动能__ _,势能_ _。
(填“变大”或“变小”)
变大
变小
3.一架飞机在灾区上方水平匀速飞行,并不断向灾区空投救灾物资,则飞机在这个过程中,动能_____,势能____。(填“变大”或“变小”)
变小
变小
4.下列哪个物体没有弹性势能( )
A.压缩的弹簧 B.踏上运动员的跳板
C.变瘪的橡皮泥 D.躺着人的弹簧床
C
谢 谢
同课章节目录
- 第一章 常见的运动
- 一、长度和时间的测量
- 二、机械运动
- 三、比较运动的快慢
- 四、学生实验:测量速度
- 五、声音的产生和传播
- 六、乐音和噪声
- 七、超声波及其应用
- 课外探究 水杯琴
- 第二章 质量和密度
- 一、质量及测量
- 二、学生实验:测量质量
- 三、物质的密度及其应用
- 四、学生实验:测量密度
- 第三章 运动和力
- 一、力
- 二、力的测量
- 三、重力
- 四、二力平衡
- 五、滑动摩擦力
- 六、运动和力的关系
- 课外探究 防滑运动鞋
- 第四章 压强与浮力
- 一、压力 压强
- 二、探究液体压强
- 三、连通器
- 四、大气压强
- 五、液体的压强与流速的关系
- 六、浮力
- 七、物体的浮沉条件
- 第五章 简单机械
- 一、杠杆
- 二、学生实验:探究杠杆
- 三、滑轮
- 课外探究 变速自行车
- 第六章 功和能
- 一、功
- 二、功率
- 三、功的原理
- 四、机械能
- 第七章 热现象
- 一、温度、温度计
- 二、熔化和凝固
- 三、汽化和液化
- 四、升华和凝华
- 五、物质结构的微观模型
- 六、内能 能量转化
- 七、比热容
- 八、燃料 能源与环保
- 九、热机
- 第八章 光现象
- 一、光的传播
- 二、学生实验:探究光的反射规律
- 三、学生实验:探究平面镜成像
- 四、探究光的折射现象
- 五、透镜
- 六、学生实验:探究凸透镜成像
- 七、生活中的透镜
- 八、眼睛和眼镜
- 九、物体的颜色
