人教版七年级数学上册 2.1整式课件(第一课时)(28张PPT)
文档属性
| 名称 | 人教版七年级数学上册 2.1整式课件(第一课时)(28张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1018.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-20 00:00:00 | ||
图片预览








文档简介
2.1 整式
第一课时
第二章 整式的加减
【学习目标】
准确理解用字母表示数的意义。
掌握用字母表示数和数量关系的规律和方法。
培养观察、分析、抽象、概括等思维能力和应用意识。
【课前预习】
1.式子a2+b2用文字语言叙述,其中不正确的是( )
A.a,b两数的平方和 B.a与b的和的平方 C.a2与b2的和 D.边长为a的正方形与边长为b的正方形的面积和
2.某商店举办促销活动,促销的方法是将原价为x元的衣服以0.6(x-10)元出售,则下列说法中,能正确表达该商店促销方法的是( )
A.原价减去10元后再打6折 B.原价打6折后再减去10元
C.原价减去10元后再打4折 D.原价打4折后再减去10元
3.x表示一个两位数,y表示一个三位数,如果把x放在y的左边组成一个五位数,那么表示这个五位数的式子是( )
A.xy B.x+y C.100x+y D.1000x+y
4.有一大捆粗细均匀的钢筋,现要确定其长度,先称出这捆钢筋的总质量为m千克,再从中截出5米长的钢筋,称出它的质量为n千克,那么这捆钢筋的总长度为( ):
A.米 B.米 C.米 D.(-5)米
5.某企业今年1月份的产值为x万元,2月份比1月份减少了10%,3月份比2月份增加了15%,则3月份的产值是( )
A.(1-10%)(1+15%)x万元 B.(1-10%+15%)x万元
C.(x-10%)(x+15%)万元 D.(1+10%-15%)x万元
【课前预习】答案
1.B
2.A
3.D
4.C
5.A
【学习探究】
青藏铁路线上,在格尔木到拉萨之间有一段很长的冻土地段.列车在冻土地段的行驶速度是100 km/h.根据已知数据求出列车在冻土地段行驶的路程.
(1)2 h行驶多少千米?3 h呢?8 h呢?t h呢?
(2)字母t表示时间有什么意义?
如果用v表示速度,列车行驶的路程是多少?
(3)回顾以前所学的知识,你还能举出用字母表示数或数量关系的例子吗?
怎样分析数量关系,并用含有字母的式子表示数量关系呢?
用字母表示数
(2)绕地球飞行n周,约需90n 分钟
解:
问题1:中国在酒泉卫星发射中心用长征二号FT2火箭将天宫二号空间实验室发射升空.它在椭圆形轨道上环绕地球飞过1周,约需90分钟.试求:
(1) 绕地球飞行10周约需多少分钟?
(2)绕地球飞行n周约需多少分钟?
(1)绕地球飞行10周,约需90×10=900 (分钟)
问题2:像0,±2,±4,±6,…能被2整除的数叫做偶数;像±1, ±3,±5,…不能被2整除的数叫做奇数.
如果k表示一个整数,那么偶数表示为 ____ ,奇数表示为 ____ .
整数 … -3 -2 -1 0 1 2 3 … k …
偶数 … -6 -4 -2 0 2 4 6 … ____ …
奇数 … -7 -5 -3 -1 1 3 5 … ____ …
2k
2k-1
2k-1
2k
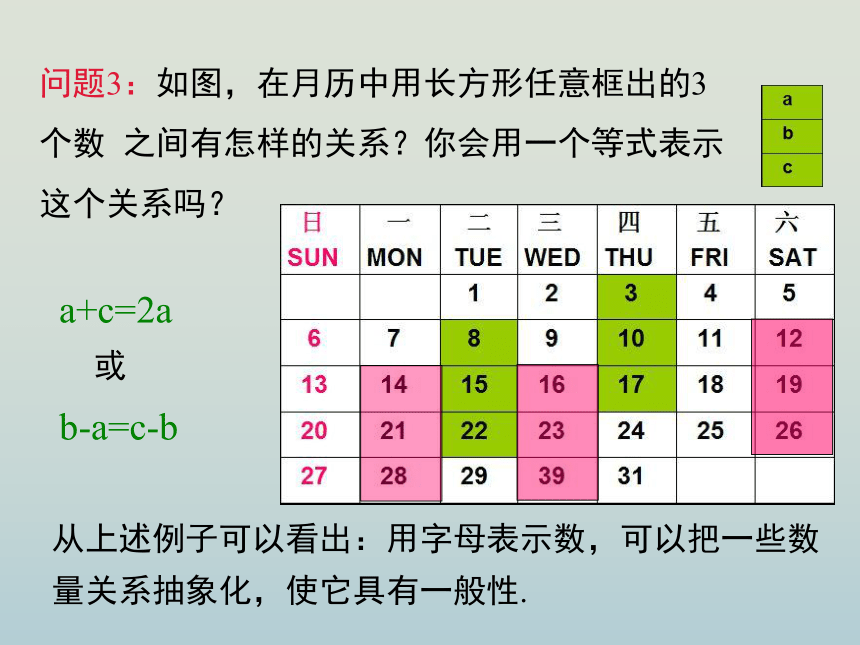
问题3:如图,在月历中用长方形任意框出的3
个数 之间有怎样的关系?你会用一个等式表示
这个关系吗?
a+c=2a
或
b-a=c-b
从上述例子可以看出:用字母表示数,可以把一些数量关系抽象化,使它具有一般性.
(1)苹果原价是每千克p元,按8折优惠出售,用式子表示现价;
(2)某产品前年的产量是n件,去年的产量是前年产量的m倍,用式子表示去年的产量;
(3)一个长方体包装盒的长和宽都是a cm,高是h cm,用式子表示它的体积;
答案:(1) 元;(2) 件;(3) cm3.
用含有字母的式子表示下列数
例1
注意带单位!
例2(1)一条河的水流速度是2.5 km/h,船在静水中的速度是 v km/h,用式子表示船在这条河中顺水行驶和逆水行驶时的速度;
分析:船在河流中行驶时,船的速度需要分两种情况讨论:
顺水行驶时,船的速度=船在静水中的速度+水流速度;
逆水行驶时,船的速度=船在静水中的速度-水流速度.
解:(1)船在这条河中顺水行驶的速度是
km/h,逆水行驶的速度是
km/h.
(2)买一个篮球需要x元,买一个排球需要y元,买一个足球需要 z 元,用式子表示买 3个篮球、5个排球、2个足球共需要的钱数;
解:(2)买3个篮球、5个排球、2个足球共需要 元.
(3)如左下图(图中长度单位:cm),用式子表示三角尺的面积;
解:(3)三角尺的面积(单位:cm2 )是 .
(4)右下图是一所住宅的建筑平面图(图中长度单位:m),用式子表示这所住宅的建筑面积.
解:(4)这所住宅的建筑面积(单位:m2)是 .
列式就是把实际问题中与数量有关的语句,用含有数、字母和运算符号的式子表示出来,也就是把文字语言转化为符号语言.
①要抓住关键词语,明确它们的意义以及它们之间的关系,如和、差、积、商及大、小、多、少、倍、分、倒数、相反数等;
②理清语句层次明确运算顺序;
③牢记一些概念和公式.
归纳:
强调: 在含有字母的式子中如果出现乘号,通常将乘号写作“·”或省略不写.例如,100×t可以写成100 ·t或100t.
归纳:
列式时:
①数与字母、字母与字母相乘省略乘号;
②数与字母相乘时数字在前;
③式子中出现除法运算时,一般按分数形式来写;
④带分数与字母相乘时,把带分数化成假分数;
⑤带单位时,适当加括号.
用字母表示数,字母和数一样可以参与运算,可以用式子把数量关系简明地表示出来.
运算定律
字母表示
加法交换律
加法结合律
乘法交换律
乘法结合律
乘法分配律
a + b = b + a
(a + b) +c= a +(b + c)
ab = ba
(ab)c = a(bc)
(a + b) c = ac+bc
1.用字母表示数的运算律
用字母表示运算律和公式
2.用字母表示有关图形的周长和面积计算公式:
名称
图形
用字母表示公式
周长(C)
面积(S)
长方形
三角形
梯形
圆
b
a
a
b
c
h
b
h
c
d
a
r
例3 (1)小明步行上学,速度为v米/秒,亮亮骑自行车上学,速度是小明的3倍, 则亮亮的速度可以表示为____米/秒.
(2)如图, 用字母表示图中阴影
部分的面积是_________
m
n
p
q
3v
一个正方形盒子的棱长为acm,用含a的式子表示:
盒子的表面积S=____________;
盒子的体积V=____________.
(1)买一个篮球需要x元,买一个排球需要y元,买一个足球需要 z 元,用式子表示买 3个篮球、5个排球、2个足球共需要的钱数。
例4
用含字母的式子表示数量关系
解:买3个篮球、5个排球、2个足球共需要
元.
1.我们现在讨论的数的范围是有理数,即数a可以是正数,也可以是负数或零,所以a不一定表示正数,-a不一定表示负数.
2.同一问题中,同一字母只能表示同一个量,不能用同一字母表示几个不同的量,不同的量要用不同的字母表示.
注意:
(1)某种商品每袋4.8元,在一个月内的销售量是m 袋,用式子表示在这个月内销售这种商品的收入.
(2)圆柱体的底面半径、高分别是 r,h,用式子表示圆柱体的体积.
【课后练习】
1.有三个连续偶数,最大的一个是2n+2,则最小的一个可以表示为( )
A.2n-2 B.2n C.2n+1 D.2n-1
2.车上有100袋面粉,每袋50千克,取下x袋,车上还有面粉( )
A.50(100-x)千克 B.(50×100-x)千克 C.100(50-x)千克 D.50x千克
3.某养殖场年底的生猪出栏价格是每千克a元.受市场影响,第二年第一季度出栏价格平均每千克下降了15%,到了第二季度平均每千克比第一季度又上升了20%,则第三季度初这家养殖场的生猪出栏价格是每千克( )
A.(1-15%)(1+20%)a元 B.(1-15%)20%a元
C.(1+15%)(1-20%)a元 D.(1+20%)15%a元
4.“x的2倍与5的和”用代数式表示为________.
5.为落实“阳光体育”工程,某校计划购买m个篮球和n个排球,已知篮球每个80元,排球每个60元,购买这些篮球和排球的总费用为________元.
【课后练习】答案
1.A 2.A 3.A 4.2x+5
5.(80m+60n)
6.(125+5x) (135 +4.5x)
7.(n+1)(2n-1)
8.(1)表格如下:
(2)由(1)知搭第n个图形需要(4n+1)根小木棒,第n个图形共有2n个三角形.
{5940675A-B579-460E-94D1-54222C63F5DA}图形标号
①
②
③
④
小木棒根数
5
9
13
17
三角形个数
2
4
6
8
第一课时
第二章 整式的加减
【学习目标】
准确理解用字母表示数的意义。
掌握用字母表示数和数量关系的规律和方法。
培养观察、分析、抽象、概括等思维能力和应用意识。
【课前预习】
1.式子a2+b2用文字语言叙述,其中不正确的是( )
A.a,b两数的平方和 B.a与b的和的平方 C.a2与b2的和 D.边长为a的正方形与边长为b的正方形的面积和
2.某商店举办促销活动,促销的方法是将原价为x元的衣服以0.6(x-10)元出售,则下列说法中,能正确表达该商店促销方法的是( )
A.原价减去10元后再打6折 B.原价打6折后再减去10元
C.原价减去10元后再打4折 D.原价打4折后再减去10元
3.x表示一个两位数,y表示一个三位数,如果把x放在y的左边组成一个五位数,那么表示这个五位数的式子是( )
A.xy B.x+y C.100x+y D.1000x+y
4.有一大捆粗细均匀的钢筋,现要确定其长度,先称出这捆钢筋的总质量为m千克,再从中截出5米长的钢筋,称出它的质量为n千克,那么这捆钢筋的总长度为( ):
A.米 B.米 C.米 D.(-5)米
5.某企业今年1月份的产值为x万元,2月份比1月份减少了10%,3月份比2月份增加了15%,则3月份的产值是( )
A.(1-10%)(1+15%)x万元 B.(1-10%+15%)x万元
C.(x-10%)(x+15%)万元 D.(1+10%-15%)x万元
【课前预习】答案
1.B
2.A
3.D
4.C
5.A
【学习探究】
青藏铁路线上,在格尔木到拉萨之间有一段很长的冻土地段.列车在冻土地段的行驶速度是100 km/h.根据已知数据求出列车在冻土地段行驶的路程.
(1)2 h行驶多少千米?3 h呢?8 h呢?t h呢?
(2)字母t表示时间有什么意义?
如果用v表示速度,列车行驶的路程是多少?
(3)回顾以前所学的知识,你还能举出用字母表示数或数量关系的例子吗?
怎样分析数量关系,并用含有字母的式子表示数量关系呢?
用字母表示数
(2)绕地球飞行n周,约需90n 分钟
解:
问题1:中国在酒泉卫星发射中心用长征二号FT2火箭将天宫二号空间实验室发射升空.它在椭圆形轨道上环绕地球飞过1周,约需90分钟.试求:
(1) 绕地球飞行10周约需多少分钟?
(2)绕地球飞行n周约需多少分钟?
(1)绕地球飞行10周,约需90×10=900 (分钟)
问题2:像0,±2,±4,±6,…能被2整除的数叫做偶数;像±1, ±3,±5,…不能被2整除的数叫做奇数.
如果k表示一个整数,那么偶数表示为 ____ ,奇数表示为 ____ .
整数 … -3 -2 -1 0 1 2 3 … k …
偶数 … -6 -4 -2 0 2 4 6 … ____ …
奇数 … -7 -5 -3 -1 1 3 5 … ____ …
2k
2k-1
2k-1
2k
问题3:如图,在月历中用长方形任意框出的3
个数 之间有怎样的关系?你会用一个等式表示
这个关系吗?
a+c=2a
或
b-a=c-b
从上述例子可以看出:用字母表示数,可以把一些数量关系抽象化,使它具有一般性.
(1)苹果原价是每千克p元,按8折优惠出售,用式子表示现价;
(2)某产品前年的产量是n件,去年的产量是前年产量的m倍,用式子表示去年的产量;
(3)一个长方体包装盒的长和宽都是a cm,高是h cm,用式子表示它的体积;
答案:(1) 元;(2) 件;(3) cm3.
用含有字母的式子表示下列数
例1
注意带单位!
例2(1)一条河的水流速度是2.5 km/h,船在静水中的速度是 v km/h,用式子表示船在这条河中顺水行驶和逆水行驶时的速度;
分析:船在河流中行驶时,船的速度需要分两种情况讨论:
顺水行驶时,船的速度=船在静水中的速度+水流速度;
逆水行驶时,船的速度=船在静水中的速度-水流速度.
解:(1)船在这条河中顺水行驶的速度是
km/h,逆水行驶的速度是
km/h.
(2)买一个篮球需要x元,买一个排球需要y元,买一个足球需要 z 元,用式子表示买 3个篮球、5个排球、2个足球共需要的钱数;
解:(2)买3个篮球、5个排球、2个足球共需要 元.
(3)如左下图(图中长度单位:cm),用式子表示三角尺的面积;
解:(3)三角尺的面积(单位:cm2 )是 .
(4)右下图是一所住宅的建筑平面图(图中长度单位:m),用式子表示这所住宅的建筑面积.
解:(4)这所住宅的建筑面积(单位:m2)是 .
列式就是把实际问题中与数量有关的语句,用含有数、字母和运算符号的式子表示出来,也就是把文字语言转化为符号语言.
①要抓住关键词语,明确它们的意义以及它们之间的关系,如和、差、积、商及大、小、多、少、倍、分、倒数、相反数等;
②理清语句层次明确运算顺序;
③牢记一些概念和公式.
归纳:
强调: 在含有字母的式子中如果出现乘号,通常将乘号写作“·”或省略不写.例如,100×t可以写成100 ·t或100t.
归纳:
列式时:
①数与字母、字母与字母相乘省略乘号;
②数与字母相乘时数字在前;
③式子中出现除法运算时,一般按分数形式来写;
④带分数与字母相乘时,把带分数化成假分数;
⑤带单位时,适当加括号.
用字母表示数,字母和数一样可以参与运算,可以用式子把数量关系简明地表示出来.
运算定律
字母表示
加法交换律
加法结合律
乘法交换律
乘法结合律
乘法分配律
a + b = b + a
(a + b) +c= a +(b + c)
ab = ba
(ab)c = a(bc)
(a + b) c = ac+bc
1.用字母表示数的运算律
用字母表示运算律和公式
2.用字母表示有关图形的周长和面积计算公式:
名称
图形
用字母表示公式
周长(C)
面积(S)
长方形
三角形
梯形
圆
b
a
a
b
c
h
b
h
c
d
a
r
例3 (1)小明步行上学,速度为v米/秒,亮亮骑自行车上学,速度是小明的3倍, 则亮亮的速度可以表示为____米/秒.
(2)如图, 用字母表示图中阴影
部分的面积是_________
m
n
p
q
3v
一个正方形盒子的棱长为acm,用含a的式子表示:
盒子的表面积S=____________;
盒子的体积V=____________.
(1)买一个篮球需要x元,买一个排球需要y元,买一个足球需要 z 元,用式子表示买 3个篮球、5个排球、2个足球共需要的钱数。
例4
用含字母的式子表示数量关系
解:买3个篮球、5个排球、2个足球共需要
元.
1.我们现在讨论的数的范围是有理数,即数a可以是正数,也可以是负数或零,所以a不一定表示正数,-a不一定表示负数.
2.同一问题中,同一字母只能表示同一个量,不能用同一字母表示几个不同的量,不同的量要用不同的字母表示.
注意:
(1)某种商品每袋4.8元,在一个月内的销售量是m 袋,用式子表示在这个月内销售这种商品的收入.
(2)圆柱体的底面半径、高分别是 r,h,用式子表示圆柱体的体积.
【课后练习】
1.有三个连续偶数,最大的一个是2n+2,则最小的一个可以表示为( )
A.2n-2 B.2n C.2n+1 D.2n-1
2.车上有100袋面粉,每袋50千克,取下x袋,车上还有面粉( )
A.50(100-x)千克 B.(50×100-x)千克 C.100(50-x)千克 D.50x千克
3.某养殖场年底的生猪出栏价格是每千克a元.受市场影响,第二年第一季度出栏价格平均每千克下降了15%,到了第二季度平均每千克比第一季度又上升了20%,则第三季度初这家养殖场的生猪出栏价格是每千克( )
A.(1-15%)(1+20%)a元 B.(1-15%)20%a元
C.(1+15%)(1-20%)a元 D.(1+20%)15%a元
4.“x的2倍与5的和”用代数式表示为________.
5.为落实“阳光体育”工程,某校计划购买m个篮球和n个排球,已知篮球每个80元,排球每个60元,购买这些篮球和排球的总费用为________元.
【课后练习】答案
1.A 2.A 3.A 4.2x+5
5.(80m+60n)
6.(125+5x) (135 +4.5x)
7.(n+1)(2n-1)
8.(1)表格如下:
(2)由(1)知搭第n个图形需要(4n+1)根小木棒,第n个图形共有2n个三角形.
{5940675A-B579-460E-94D1-54222C63F5DA}图形标号
①
②
③
④
小木棒根数
5
9
13
17
三角形个数
2
4
6
8
