人教(五四制) 八上23.3 二次根式的加减 (阅读与思考) 课件 (共11张ppt)
文档属性
| 名称 | 人教(五四制) 八上23.3 二次根式的加减 (阅读与思考) 课件 (共11张ppt) |
|
|
| 格式 | ppt | ||
| 文件大小 | 408.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-21 00:00:00 | ||
图片预览


文档简介
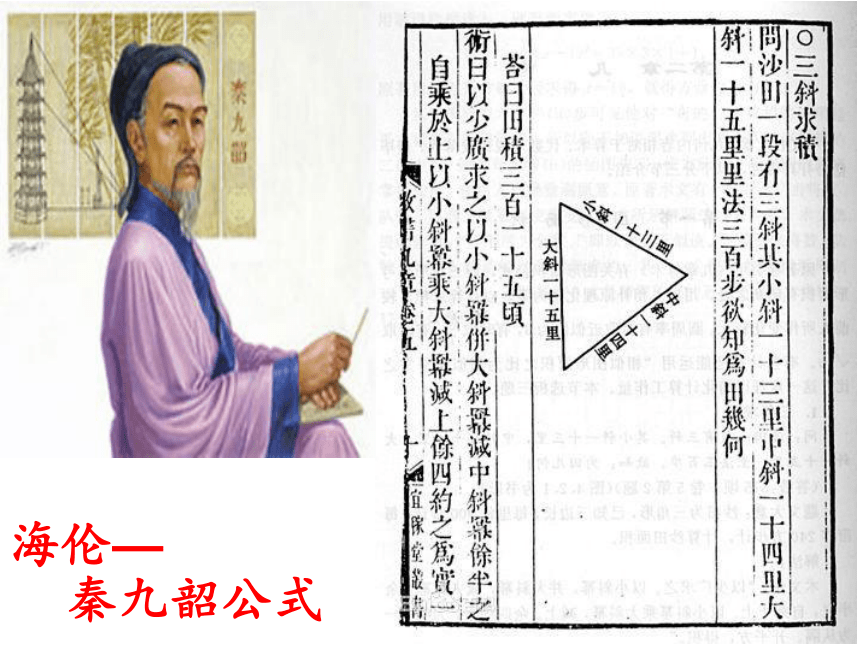
海伦—
秦九韶公式
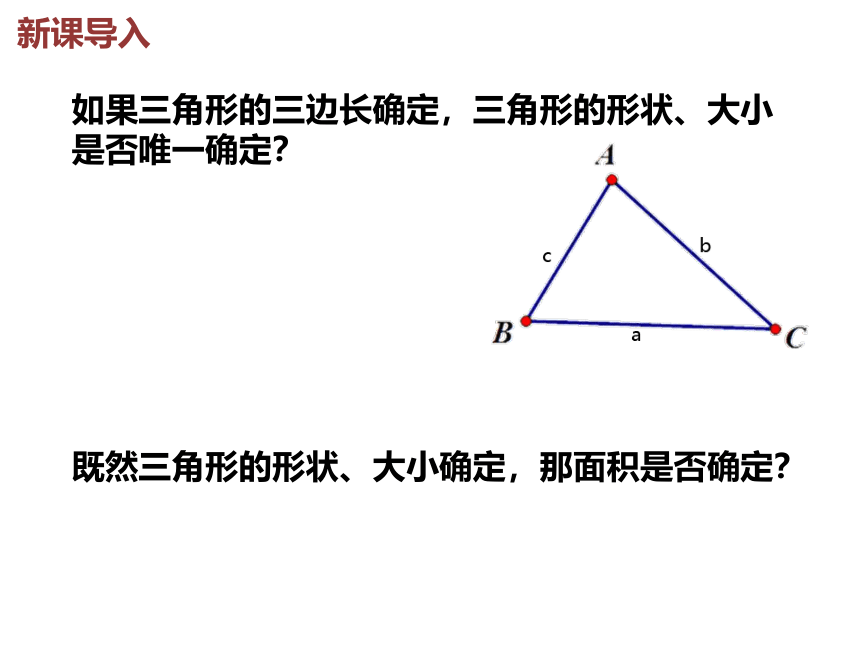
如果三角形的三边长确定,三角形的形状、大小是否唯一确定?
新课导入
既然三角形的形状、大小确定,那面积是否确定?
新课导入
D
D
∵AD⊥BC ∴∠ADB=∠ADC=90°
∴在Rt△ABD中,AD2+BD2=AB2
在Rt△ACD中,AD2+CD2=AC2
∴AB2-BD2=AD2=AC2-CD2
即22 -(4-x)2=32-x2
x2 - (4-x)2=32 - 22
8x - 42=32 - 22
8x=42 +32 - 22
∴x=
∴AD2=AC2-CD2=32 - x2=
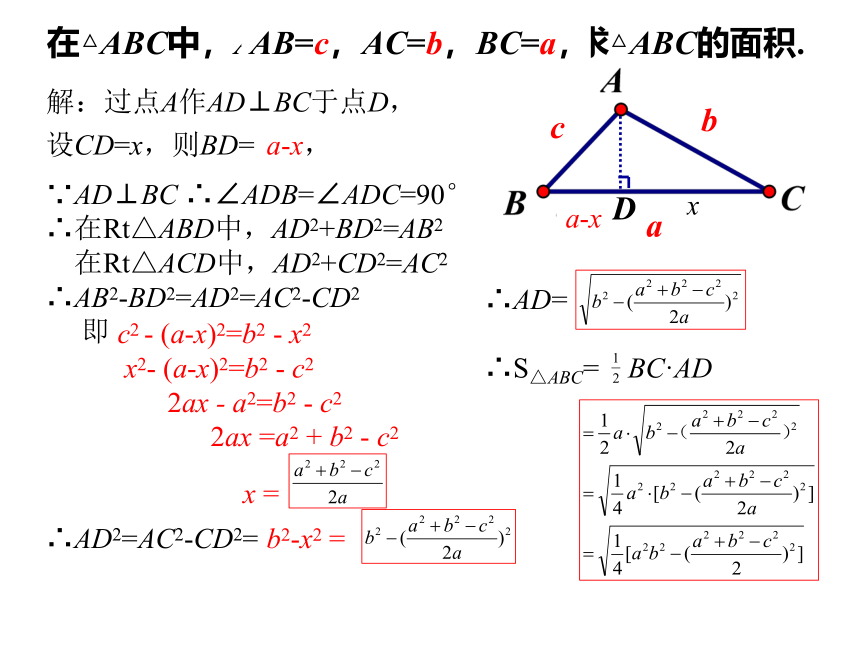
在△ABC中,AB=2,AC=3,BC=4,求△ABC的面积.
解:过点A作AD⊥BC于点D,
D
设CD=x,则BD= 4-x,
4-x
x
AB=c,AC=b,BC=a,
a
b
c
a-x,
a-x
c2 - (a-x)2=b2 - x2
x2- (a-x)2=b2 - c2
2ax - a2=b2 - c2
2ax =a2 + b2 - c2
x =
∴AD=
∴S△ABC= BC·AD
=
b2-x2 =
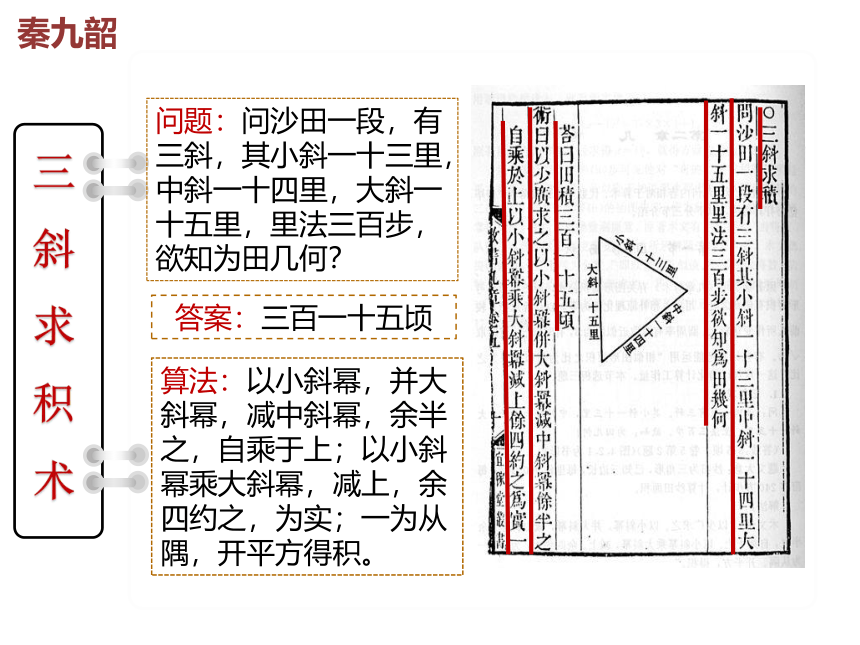
算法:以小斜幂,并大斜幂,减中斜幂,余半之,自乘于上;以小斜幂乘大斜幂,减上,余四约之,为实;一为从隅,开平方得积。
三斜求积术
问题:问沙田一段,有三斜,其小斜一十三里,中斜一十四里,大斜一十五里,里法三百步,欲知为田几何?
答案:三百一十五顷
秦九韶
秦九韶公式
若以大斜记为a ,小斜记为b ,中斜记为c ,
用现代公式表示即为:
算法:以小斜幂,并大斜幂,减中斜幂,余半之,自乘于上;以小斜幂乘大斜幂,减上,余四约之,为实;一为从隅,开平方得积。
秦九韶公式
海伦,古希腊数学家、力学家、机械学家。
海伦公式出现在海伦(约公元50年)的《测地术》一书中,海伦用文字在《经纬仪》和《度量》两书中都叙述了这一公式的证明。虽然现已公认,此公式是阿基米德(约公元前287—前212)发现的,但习惯成自然,我们仍称之为海伦公式。
海伦公式
海伦公式的提出为三角形和多边形的面积计算提供了新的方法和思路,在知道三角形三边的长而不知道高的情况下使用海伦公式可以更快更简便的求出面积。
比如说在测量土地的面积的时候,不用测三角形的高,只需测两点间的距离,就可以方便地得出答案。
海伦公式
在△ABC中,AB=2,AC=3,BC=4,求△ABC的面积.
公式的应用
课堂小结
课堂小结
这节课你有什么收获?
谢谢
秦九韶公式
如果三角形的三边长确定,三角形的形状、大小是否唯一确定?
新课导入
既然三角形的形状、大小确定,那面积是否确定?
新课导入
D
D
∵AD⊥BC ∴∠ADB=∠ADC=90°
∴在Rt△ABD中,AD2+BD2=AB2
在Rt△ACD中,AD2+CD2=AC2
∴AB2-BD2=AD2=AC2-CD2
即22 -(4-x)2=32-x2
x2 - (4-x)2=32 - 22
8x - 42=32 - 22
8x=42 +32 - 22
∴x=
∴AD2=AC2-CD2=32 - x2=
在△ABC中,AB=2,AC=3,BC=4,求△ABC的面积.
解:过点A作AD⊥BC于点D,
D
设CD=x,则BD= 4-x,
4-x
x
AB=c,AC=b,BC=a,
a
b
c
a-x,
a-x
c2 - (a-x)2=b2 - x2
x2- (a-x)2=b2 - c2
2ax - a2=b2 - c2
2ax =a2 + b2 - c2
x =
∴AD=
∴S△ABC= BC·AD
=
b2-x2 =
算法:以小斜幂,并大斜幂,减中斜幂,余半之,自乘于上;以小斜幂乘大斜幂,减上,余四约之,为实;一为从隅,开平方得积。
三斜求积术
问题:问沙田一段,有三斜,其小斜一十三里,中斜一十四里,大斜一十五里,里法三百步,欲知为田几何?
答案:三百一十五顷
秦九韶
秦九韶公式
若以大斜记为a ,小斜记为b ,中斜记为c ,
用现代公式表示即为:
算法:以小斜幂,并大斜幂,减中斜幂,余半之,自乘于上;以小斜幂乘大斜幂,减上,余四约之,为实;一为从隅,开平方得积。
秦九韶公式
海伦,古希腊数学家、力学家、机械学家。
海伦公式出现在海伦(约公元50年)的《测地术》一书中,海伦用文字在《经纬仪》和《度量》两书中都叙述了这一公式的证明。虽然现已公认,此公式是阿基米德(约公元前287—前212)发现的,但习惯成自然,我们仍称之为海伦公式。
海伦公式
海伦公式的提出为三角形和多边形的面积计算提供了新的方法和思路,在知道三角形三边的长而不知道高的情况下使用海伦公式可以更快更简便的求出面积。
比如说在测量土地的面积的时候,不用测三角形的高,只需测两点间的距离,就可以方便地得出答案。
海伦公式
在△ABC中,AB=2,AC=3,BC=4,求△ABC的面积.
公式的应用
课堂小结
课堂小结
这节课你有什么收获?
谢谢
