人教版数学八年级上册11.1.1三角形三边的关系课件(共14张)
文档属性
| 名称 | 人教版数学八年级上册11.1.1三角形三边的关系课件(共14张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-20 00:00:00 | ||
图片预览





文档简介
三角形三边的关系
三角形的三边之间有什么关系?
如何根据三边关系判断三条线段能否组成三角形?
学习目标
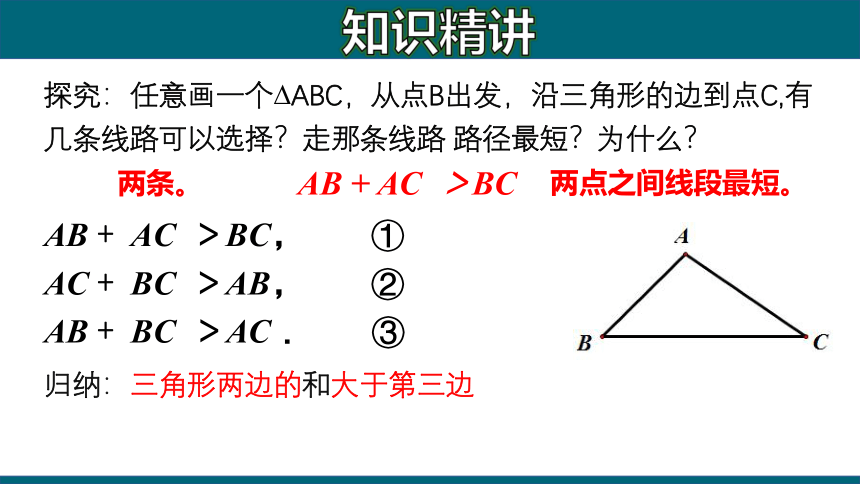
探究:任意画一个?ABC,从点B出发,沿三角形的边到点C,有几条线路可以选择?走那条线路 路径最短?为什么?
归纳:三角形两边的和大于第三边
AB + AC >BC, ①
AC + BC >AB, ②
AB + BC >AC. ③
两条。
两点之间线段最短。
AB + AC >BC
知识精讲
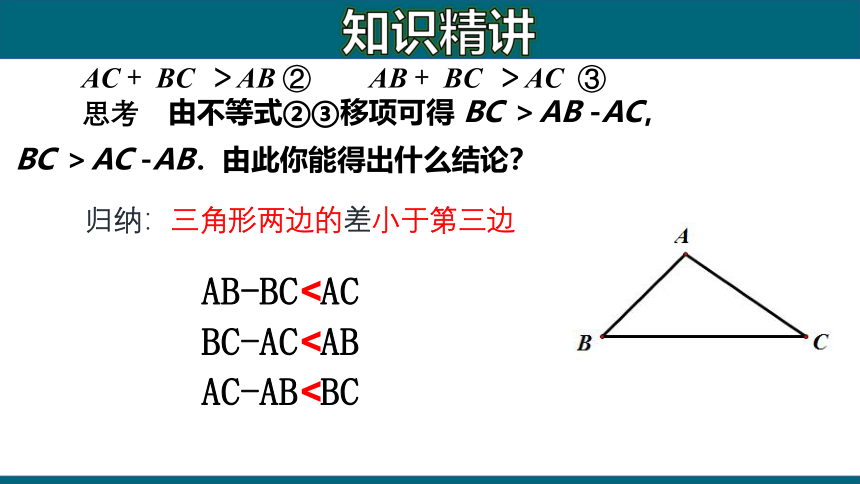
归纳:三角形两边的差小于第三边
思考 由不等式②③移项可得 BC >AB -AC,
BC >AC -AB.由此你能得出什么结论?
AB-BCBC-ACAC-AB知识精讲
AC + BC >AB ② AB + BC >AC ③
在△ABC中,若b =3,a=7,则第
三边c的取值范围是 。
既要考虑“两边之和大于第三边”,
又要考虑“两边之差小于第三边”
a - b < c < a + b
4 < c < 10
典例解析
变式:在△ABC中,若b=3,a=7,则其周长l的取值范围是 。
14 < l< 20
典例解析
解:(1)能.因为3 + 4>5,
符合三角形两边的和大于第三边。
(2)不能.因为5 + 6 =11,
不符合三角形两边的和大于第三边。
(3)能.因为5 + 6>10,
符合三角形两边的和大于第三边。
例. 下列长度的三条线段能否组成三角形?为什么?
(1)3,4,5;(2)5,6,11;(3)5,6,10。
典例解析
用较小两条线段的和与第三条线段做比较;
若较小两条线段的和大于第三条线段,就能保证
任意两条线段的和大于第三条线段。
思考 解决这类问题我们通常用哪两条线段的和与第三条线段做比较就可以了?为什么?
知识精讲
已知,三角形有两条边长分别为5、8,求第三条边的
取值范围。
巩固训练
判断下列每组线段能否组成三角形(能的在括号中打“√”,不能的打“×”)
(1)a=5,b=4,c=3; ( )
(2)a=7,b=2,c=4; ( )
(3)a=6,b=6,c=12; ( )
(4)a=6,b=5,c=5。 ( )
√
×
×
√
巩固训练
例. 用一条长为18 cm的细绳围成一个等腰三角
形.能围成有一边的长为4 cm的等腰三角形吗?为什么?
解:?如果4 cm长的边为底边,设腰长为x cm,则
4 + 2x = 18 解得 x = 7
此时三边分别为4cm,7cm,7cm
?如果4 cm长的边为腰,设底边长为x cm,
则4+4 + x = 18. 解得 x = 10
此时三边分别为4cm,4cm,10cm
因为4 + 4<10,
由以上讨论可知,可以围成底边长为4 cm,的等腰三角形。
不符合三角形两边的和大于第三边,
所以不能围成腰长为4cm 的等腰三角形。
巩固训练
已知a、b、c为△ABC的三边长,满足(b-2)?+ ▏c-3 ▏=0,且 a 是方程 ▏x-4 ▏=2的解。求△ABC的周长。并判断△ABC的形状。
巩固训练
三角形的三边关系
1、
会利用三边关系判断三边是否能组成三角形
2、
小结梳理
三角形两边的和大于第三边
三角形两边的差小于第三边
用较小两条线段的和与第三条线段做比较;
若较小两条线段的和大于第三条线段,就能保证
任意两条线段的和大于第三条线段。
三角形的三边之间有什么关系?
如何根据三边关系判断三条线段能否组成三角形?
学习目标
探究:任意画一个?ABC,从点B出发,沿三角形的边到点C,有几条线路可以选择?走那条线路 路径最短?为什么?
归纳:三角形两边的和大于第三边
AB + AC >BC, ①
AC + BC >AB, ②
AB + BC >AC. ③
两条。
两点之间线段最短。
AB + AC >BC
知识精讲
归纳:三角形两边的差小于第三边
思考 由不等式②③移项可得 BC >AB -AC,
BC >AC -AB.由此你能得出什么结论?
AB-BC
AC + BC >AB ② AB + BC >AC ③
在△ABC中,若b =3,a=7,则第
三边c的取值范围是 。
既要考虑“两边之和大于第三边”,
又要考虑“两边之差小于第三边”
a - b < c < a + b
4 < c < 10
典例解析
变式:在△ABC中,若b=3,a=7,则其周长l的取值范围是 。
14 < l< 20
典例解析
解:(1)能.因为3 + 4>5,
符合三角形两边的和大于第三边。
(2)不能.因为5 + 6 =11,
不符合三角形两边的和大于第三边。
(3)能.因为5 + 6>10,
符合三角形两边的和大于第三边。
例. 下列长度的三条线段能否组成三角形?为什么?
(1)3,4,5;(2)5,6,11;(3)5,6,10。
典例解析
用较小两条线段的和与第三条线段做比较;
若较小两条线段的和大于第三条线段,就能保证
任意两条线段的和大于第三条线段。
思考 解决这类问题我们通常用哪两条线段的和与第三条线段做比较就可以了?为什么?
知识精讲
已知,三角形有两条边长分别为5、8,求第三条边的
取值范围。
巩固训练
判断下列每组线段能否组成三角形(能的在括号中打“√”,不能的打“×”)
(1)a=5,b=4,c=3; ( )
(2)a=7,b=2,c=4; ( )
(3)a=6,b=6,c=12; ( )
(4)a=6,b=5,c=5。 ( )
√
×
×
√
巩固训练
例. 用一条长为18 cm的细绳围成一个等腰三角
形.能围成有一边的长为4 cm的等腰三角形吗?为什么?
解:?如果4 cm长的边为底边,设腰长为x cm,则
4 + 2x = 18 解得 x = 7
此时三边分别为4cm,7cm,7cm
?如果4 cm长的边为腰,设底边长为x cm,
则4+4 + x = 18. 解得 x = 10
此时三边分别为4cm,4cm,10cm
因为4 + 4<10,
由以上讨论可知,可以围成底边长为4 cm,的等腰三角形。
不符合三角形两边的和大于第三边,
所以不能围成腰长为4cm 的等腰三角形。
巩固训练
已知a、b、c为△ABC的三边长,满足(b-2)?+ ▏c-3 ▏=0,且 a 是方程 ▏x-4 ▏=2的解。求△ABC的周长。并判断△ABC的形状。
巩固训练
三角形的三边关系
1、
会利用三边关系判断三边是否能组成三角形
2、
小结梳理
三角形两边的和大于第三边
三角形两边的差小于第三边
用较小两条线段的和与第三条线段做比较;
若较小两条线段的和大于第三条线段,就能保证
任意两条线段的和大于第三条线段。
