人教版数学八年级上册11.1 三角形的“三线”综合应用课件(共22张)
文档属性
| 名称 | 人教版数学八年级上册11.1 三角形的“三线”综合应用课件(共22张) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-20 23:20:18 | ||
图片预览





文档简介
三角形的“三线”综合应用
学习目标
熟练掌握三角形高线、中线、角平分线的定义.
三角形的“三线”综合应用.
基础训练
1.下列说法中正确的是( )
A.三角形的三条高都在三角形内
B.直角三角形只有一条高
C.锐角三角形的三条高都在三角形内
D.三角形每一边上的高都小于其他两边
C
2.若AD是△ABC的中线,下列结论错误的是( )
A.AB=BC
B.BD=DC
C.AD平分BC
D.BC=2DC
A
基础训练
3.【2018?杭州】若线段AM,AN分别是△ABC的BC边上的高线和中线,则( )
A.AM>AN B.AM≥AN
C.AMD
基础训练
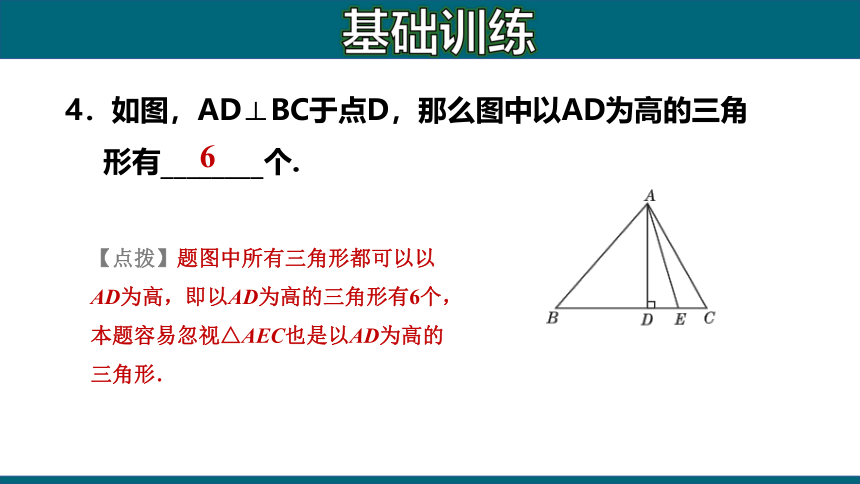
4.如图,AD⊥BC于点D,那么图中以AD为高的三角形有________个.
【点拨】题图中所有三角形都可以以AD为高,即以AD为高的三角形有6个,本题容易忽视△AEC也是以AD为高的三角形.
6
基础训练
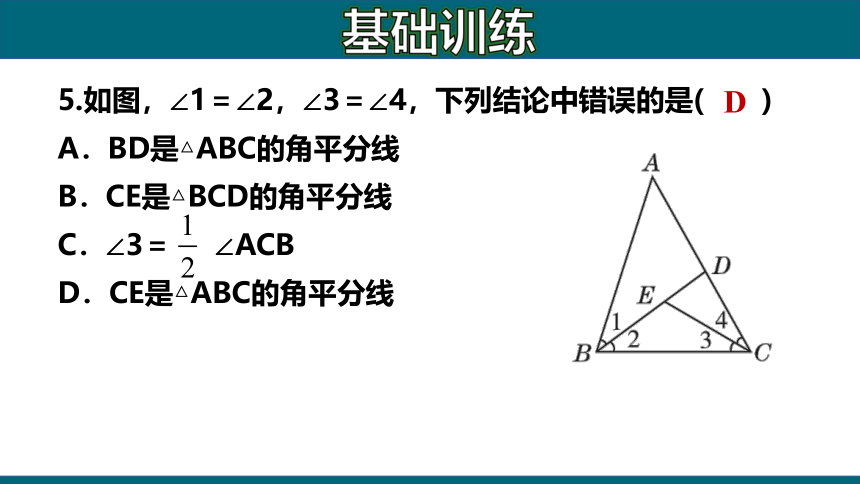
D
5.如图,∠1=∠2,∠3=∠4,下列结论中错误的是( )
A.BD是△ABC的角平分线
B.CE是△BCD的角平分线
C.∠3= ∠ACB
D.CE是△ABC的角平分线
基础训练
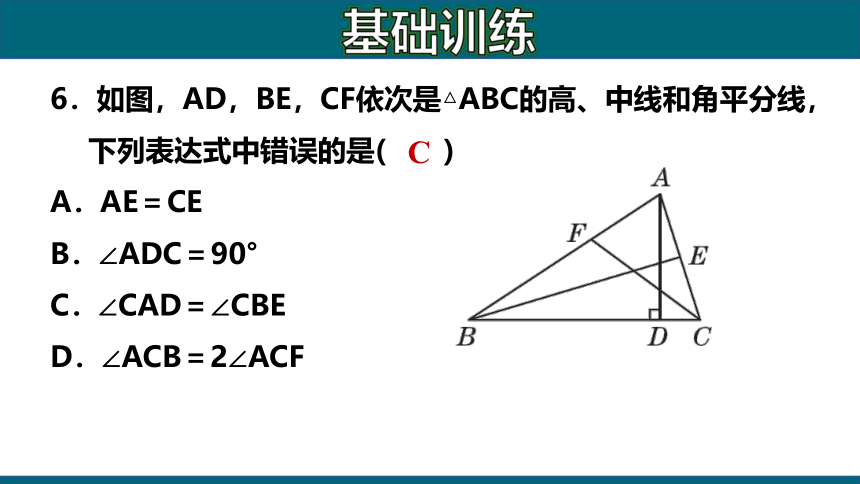
6.如图,AD,BE,CF依次是△ABC的高、中线和角平分线,下列表达式中错误的是( )
A.AE=CE
B.∠ADC=90°
C.∠CAD=∠CBE
D.∠ACB=2∠ACF
C
基础训练
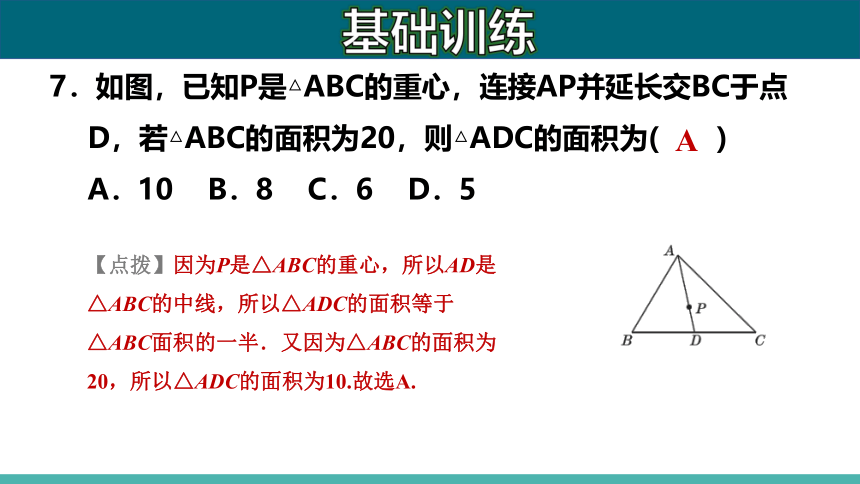
7.如图,已知P是△ABC的重心,连接AP并延长交BC于点D,若△ABC的面积为20,则△ADC的面积为( )
A.10 B.8 C.6 D.5
【点拨】因为P是△ABC的重心,所以AD是△ABC的中线,所以△ADC的面积等于△ABC面积的一半.又因为△ABC的面积为20,所以△ADC的面积为10.故选A.
A
基础训练
8.如图所示,已知AD是△ABC的边BC上的中线 。
(1)作出△ABD的边BD上的高 。
解:如图所示.AM为△ABD的边BD上的高 。
拓展提升
(2)若△ABD的面积为6,且BD边上的高为3,求BC 的长。
解:∵AD是△ABC的边BC上的中线, △ABD的面积为6,
∴△ABC的面积为12.
∵BD边上的高AM为3,
∴BC=12×2÷3=8 。
拓展提升
9.【2018?黄石】如图,△ABC中,AD是BC边上的高,AE,BF分别是∠BAC、∠ABC的平分线,∠BAC=50°,∠ABC=60°,则∠EAD+∠ACD=( )
A.75°
B.80°
C.85°
D.90°
拓展提升
【点拨】依据AD是BC边上的高,∠ABC=60°,即可得到∠BAD=30°.依据∠BAC=50°,AE平分∠BAC,即可得到∠BAE=25°,则∠DAE=5°.又∠ACD=180°-∠ABC-∠BAC=70°,则∠EAD+∠ACD=75°.
【答案】A
拓展提升
10.如图,D是△ABC中BC边上一点,DE∥AC交AB于点E,若∠EDA=∠EAD,试说明AD是△ABC的角平分线 。
解:∵DE∥AC,
∴∠EDA=∠CAD.
∵∠EDA=∠EAD,
∴∠CAD=∠EAD,
∴AD是△ABC的角平分线。
拓展提升
11.如图,在△ABC中,D,E两点分别在AB,BC上,若AD∶DB=CE∶EB=2∶3,则△DBE与△ADC的面积比为( )
A.3∶5
B.4∶5
C.9∶10
D.15∶16
拓展提升
【点拨】∵AD:DB=CE:EB=2:3,
∴S△BDC:S△ADC=3:2,S△BDE:S△DCE=3:2.
∴设S△BDC=3x,则S△ADC=2x,S△BED=1.8x,
故△DBE与△ADC的面积比为1.8x:2x=9:10.
故选C.
【答案】C
拓展提升
A
11.如图,AD是△ABC的中线,DE是△ADC的高线,AB=16,AC=22,DE=8,则点D到AB的距离是( )
A.11 B. C. D.8
拓展提升
12.如图所示,已知AD,AE分别是△ABC的高和中线,AB=6 cm,AC=8 cm,BC=10 cm,∠CAB=90°。试求:
(1)AD的长;
拓展提升
12.如图所示,已知AD,AE分别是△ABC的高和中线,AB=6 cm,AC=8 cm,BC=10 cm,∠CAB=90°。试求:(2)△ABE的面积;
拓展提升
解:∵AE为BC边上的中线,
∴BE=CE,
∴△ACE的周长-△ABE的周长=AC+AE+
CE-(AB+BE+AE)=AC-AB=8-6=2(cm)
即△ACE和△ABE的周长的差是2 cm.
12.如图所示,已知AD,AE分别是△ABC的高和中线,AB=6 cm,AC=8 cm,BC=10 cm,∠CAB=90°。试求:(3)△ACE和△ABE的周长的差.
拓展提升
小结梳理
“三线”概念的理解
1、
三角形的“三线”综合应用
2、
学习目标
熟练掌握三角形高线、中线、角平分线的定义.
三角形的“三线”综合应用.
基础训练
1.下列说法中正确的是( )
A.三角形的三条高都在三角形内
B.直角三角形只有一条高
C.锐角三角形的三条高都在三角形内
D.三角形每一边上的高都小于其他两边
C
2.若AD是△ABC的中线,下列结论错误的是( )
A.AB=BC
B.BD=DC
C.AD平分BC
D.BC=2DC
A
基础训练
3.【2018?杭州】若线段AM,AN分别是△ABC的BC边上的高线和中线,则( )
A.AM>AN B.AM≥AN
C.AM
基础训练
4.如图,AD⊥BC于点D,那么图中以AD为高的三角形有________个.
【点拨】题图中所有三角形都可以以AD为高,即以AD为高的三角形有6个,本题容易忽视△AEC也是以AD为高的三角形.
6
基础训练
D
5.如图,∠1=∠2,∠3=∠4,下列结论中错误的是( )
A.BD是△ABC的角平分线
B.CE是△BCD的角平分线
C.∠3= ∠ACB
D.CE是△ABC的角平分线
基础训练
6.如图,AD,BE,CF依次是△ABC的高、中线和角平分线,下列表达式中错误的是( )
A.AE=CE
B.∠ADC=90°
C.∠CAD=∠CBE
D.∠ACB=2∠ACF
C
基础训练
7.如图,已知P是△ABC的重心,连接AP并延长交BC于点D,若△ABC的面积为20,则△ADC的面积为( )
A.10 B.8 C.6 D.5
【点拨】因为P是△ABC的重心,所以AD是△ABC的中线,所以△ADC的面积等于△ABC面积的一半.又因为△ABC的面积为20,所以△ADC的面积为10.故选A.
A
基础训练
8.如图所示,已知AD是△ABC的边BC上的中线 。
(1)作出△ABD的边BD上的高 。
解:如图所示.AM为△ABD的边BD上的高 。
拓展提升
(2)若△ABD的面积为6,且BD边上的高为3,求BC 的长。
解:∵AD是△ABC的边BC上的中线, △ABD的面积为6,
∴△ABC的面积为12.
∵BD边上的高AM为3,
∴BC=12×2÷3=8 。
拓展提升
9.【2018?黄石】如图,△ABC中,AD是BC边上的高,AE,BF分别是∠BAC、∠ABC的平分线,∠BAC=50°,∠ABC=60°,则∠EAD+∠ACD=( )
A.75°
B.80°
C.85°
D.90°
拓展提升
【点拨】依据AD是BC边上的高,∠ABC=60°,即可得到∠BAD=30°.依据∠BAC=50°,AE平分∠BAC,即可得到∠BAE=25°,则∠DAE=5°.又∠ACD=180°-∠ABC-∠BAC=70°,则∠EAD+∠ACD=75°.
【答案】A
拓展提升
10.如图,D是△ABC中BC边上一点,DE∥AC交AB于点E,若∠EDA=∠EAD,试说明AD是△ABC的角平分线 。
解:∵DE∥AC,
∴∠EDA=∠CAD.
∵∠EDA=∠EAD,
∴∠CAD=∠EAD,
∴AD是△ABC的角平分线。
拓展提升
11.如图,在△ABC中,D,E两点分别在AB,BC上,若AD∶DB=CE∶EB=2∶3,则△DBE与△ADC的面积比为( )
A.3∶5
B.4∶5
C.9∶10
D.15∶16
拓展提升
【点拨】∵AD:DB=CE:EB=2:3,
∴S△BDC:S△ADC=3:2,S△BDE:S△DCE=3:2.
∴设S△BDC=3x,则S△ADC=2x,S△BED=1.8x,
故△DBE与△ADC的面积比为1.8x:2x=9:10.
故选C.
【答案】C
拓展提升
A
11.如图,AD是△ABC的中线,DE是△ADC的高线,AB=16,AC=22,DE=8,则点D到AB的距离是( )
A.11 B. C. D.8
拓展提升
12.如图所示,已知AD,AE分别是△ABC的高和中线,AB=6 cm,AC=8 cm,BC=10 cm,∠CAB=90°。试求:
(1)AD的长;
拓展提升
12.如图所示,已知AD,AE分别是△ABC的高和中线,AB=6 cm,AC=8 cm,BC=10 cm,∠CAB=90°。试求:(2)△ABE的面积;
拓展提升
解:∵AE为BC边上的中线,
∴BE=CE,
∴△ACE的周长-△ABE的周长=AC+AE+
CE-(AB+BE+AE)=AC-AB=8-6=2(cm)
即△ACE和△ABE的周长的差是2 cm.
12.如图所示,已知AD,AE分别是△ABC的高和中线,AB=6 cm,AC=8 cm,BC=10 cm,∠CAB=90°。试求:(3)△ACE和△ABE的周长的差.
拓展提升
小结梳理
“三线”概念的理解
1、
三角形的“三线”综合应用
2、
