13.1.2.1 线段的垂直平分线的性质和判定课件(25张PPT)
文档属性
| 名称 | 13.1.2.1 线段的垂直平分线的性质和判定课件(25张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-23 07:06:05 | ||
图片预览





文档简介
第十三章 轴对称
13.1.2 线段垂直平分线的性质
第1课时 线段的垂直平分线的性质和判定
2020年秋人教版数学八年级上册精品课件
学习目标
1
2
会用尺规过一点作已知直线的垂线.
3
能够运用线段的垂直平分线的性质和判定解决实际问题.(难点)
理解并掌握线段的垂直平分线的性质和判定方法.(重点)
新课导入
某区政府为了方便居民的生活,计划在三个住宅小区 A、B、C 之间修建一个购物中心,试问该购物中心应建于何处,才能使得它到三个小区的距离相等?
A
B
C
知识讲解
1.线段垂直平分线的性质
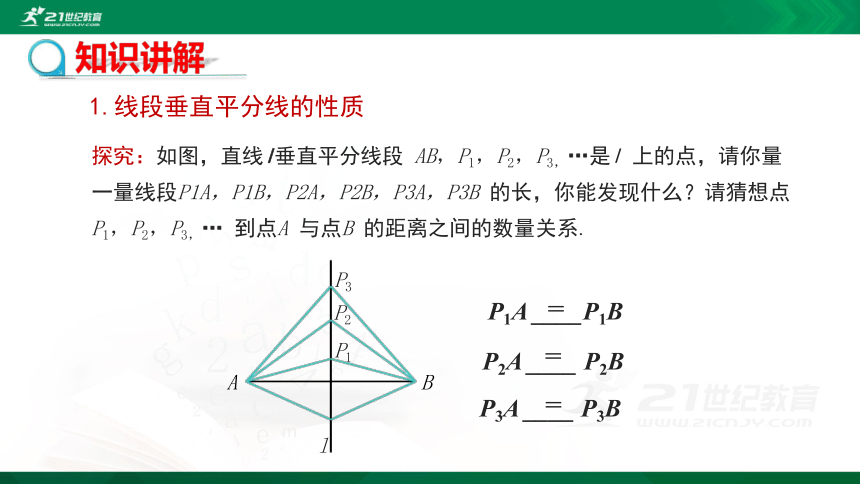
探究:如图,直线l垂直平分线段 AB,P1,P2,P3,…是l 上的点,请你量一量线段P1A,P1B,P2A,P2B,P3A,P3B 的长,你能发现什么?请猜想点P1,P2,P3,… 到点A 与点B 的距离之间的数量关系.
A
B
l
P1
P2
P3
P1A ____P1B
P2A ____ P2B
P3A ____ P3B
=
=
=
猜想:
点P1,P2,P3,… 到点 A 与点 B 的距离分别相等.
由此你能得到什么结论?
你能验证这一结论吗?
命题:线段垂直平分线上的点和这条线段两个端点的距离相等.
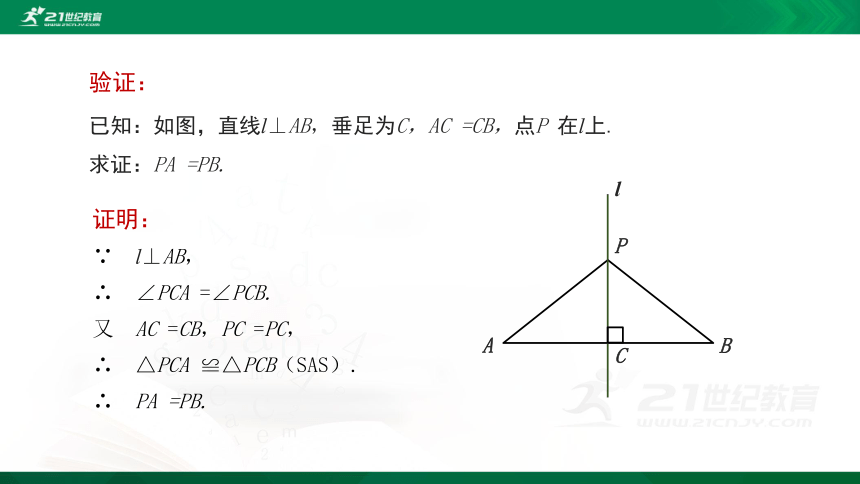
验证:
证明:
∵ l⊥AB,
∴ ∠PCA =∠PCB.
又 AC =CB,PC =PC,
∴ △PCA ≌△PCB(SAS).
∴ PA =PB.
P
A
B
l
C
已知:如图,直线l⊥AB,垂足为C,AC =CB,点P 在l上.
求证:PA =PB.
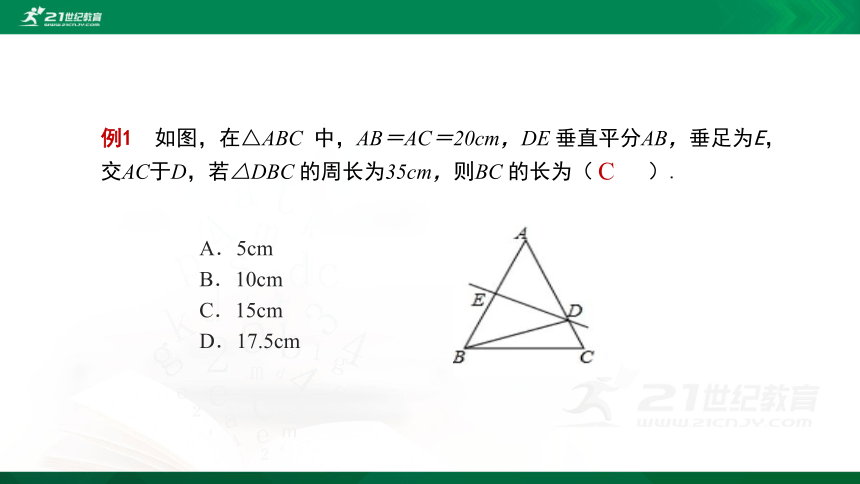
例1 如图,在△ABC 中,AB=AC=20cm,DE 垂直平分AB,垂足为E,交AC于D,若△DBC 的周长为35cm,则BC 的长为( ).
A.5cm
B.10cm
C.15cm
D.17.5cm
C
解析:
∵△DBC 的周长为BC+BD+CD=35cm,
又∵DE 垂直平分AB,
∴AD=BD,故BC+AD+CD=35cm.
∵AC=AD+DC=20cm,
∴BC=35-20=15(cm). 故选C
总结:利用线段垂直平分线的性质,实现线段之间的相互转化,从而求出未知线段的长.
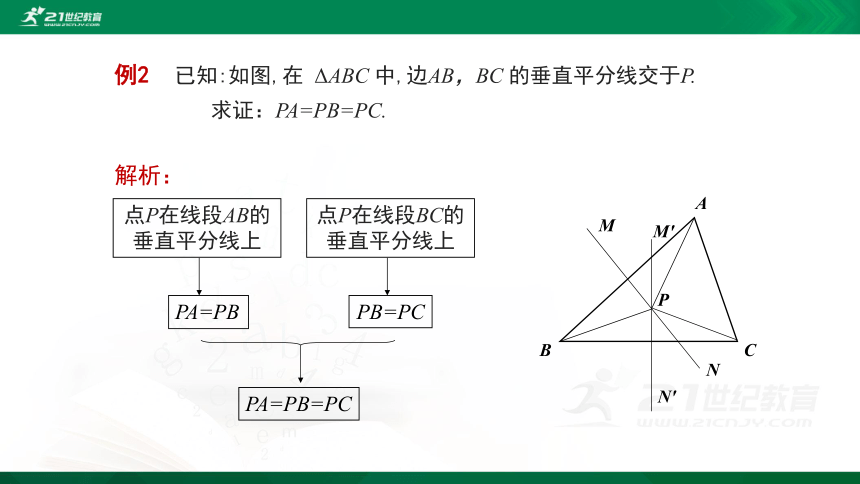
例2 已知:如图,在 ΔABC 中,边AB,BC 的垂直平分线交于P.
求证:PA=PB=PC.
B
A
C
M
N
M'
N'
P
PA=PB=PC
PB=PC
点P在线段BC的垂直平分线上
PA=PB
点P在线段AB的垂直平分线上
解析:
证明:
∵点P在线段AB的垂直平分线MN上,
∴PA=PB.
同理 PB=PC.
∴PA=PB=PC.
结论:三角形三边垂直平分线交于一点,这一点到三角形三个顶点的距离相等。
现在你能想到方法确定购物中心的位置,使得它到三个小区的距离相等吗?
想一想:如果 PA=PB ,那么点 P 是否在线段 AB 的垂直平分线上呢?
P
A
B
已知:如图,PA =PB.
求证:点P 在线段 AB 的垂直平分线上.
2、线段垂直平分线的判定
探究
证明:
过点P 作AB 的垂线PC,垂足为点C.
则∠PCA =∠PCB =90°.
在Rt△PCA 和Rt△PCB 中,
PA =PB,PC =PC,
∴ Rt△PCA ≌Rt△PCB(HL).
∴ AC =BC.
又 PC⊥AB,
∴ 点P 在线段AB 的垂直平分线上.
P
A
B
C
线段垂直平分线的判定:
与线段两个端点距离相等的点在这条线段的垂直平分线上.
应用格式:
∵ PA =PB,
∴ 点 P 在 AB 的垂直平分线上.
P
A
B
作用:
判断一个点是否在线段的垂直平分线上.
例3 尺规作图:经过已知直线外一点作这条直线的垂线.
A
B
C
D
E
K
已知:直线AB和AB外一点C .
求作:AB的垂线,使它经过点C .
作法:(1)任意取一点K,使点K和点C在AB的两旁.
(2)以点C 为圆心,CK长为半径作弧,交 AB于
点D和点E.
(4)作直线CF.
直线CF就是所求作的垂线.
(3)分别以点D和点E为圆心,大于 DE的长为
半径作弧,两弧相交于点F.
F
例4 已知:如图,点E是∠AOB的平分线上一点,EC⊥OA,ED⊥OB,
垂足分别为C,D,连接CD.
求证:OE是CD的垂直平分线.
A
B
O
E
D
C
证明:
∵OE平分∠AOB,EC⊥OA,ED⊥OB,
∴ DE=CE.
∴ OE是CD的垂直平分线.
又∵OE=OE,
∴Rt△OED≌Rt△OEC.
∴DO=CO.
随堂训练
1、如图所示,AC=AD,BC=BD,则下列说法正确的是( )
A. AB垂直平分CD;
B .CD垂直平分AB ;
C.AB与CD互相垂直平分;
D.CD平分∠ ACB.
A
2、在锐角三角形 ABC 内一点P,满足 PA=PB=PC,则点P是△ABC( )
A、三条角平分线的交点
B、三条中线的交点
C、三条高的交点
D、三边垂直平分线的交点
D
4、下列说法:
① 若点P、E是线段AB的垂直平分线上两点,则EA=EB,PA=PB;
②若PA=PB,EA=EB,则直线PE垂直平分线段AB;
③若PA=PB,则点P必是线段AB的垂直平分线上的点;
④若EA=EB,则经过点E的直线垂直平分线段AB.
其中正确的有 (填序号).
① ② ③
3、已知线段AB,在平面上找到三个点D、E、F,使DA=DB,EA=EB,FA=FB,这样的点的组合共有 种.
无数
5、如图,△ABC中,AB=AC,AB的垂直平分线交AC于E,连接BE,AB+BC=16cm,则△BCE的周长是 cm.
A
B
C
D
E
16
6、已知:如图,点C,D是线段AB外的两点,且AC =BC, AD=BD,
AB与CD相交于点O.
求证:AO=BO.
证明:
∵ AC =BC,AD=BD,
∴
点C和点D在线段AB的垂直平分线上,
∴ CD为线段AB的垂直平分线.
又 ∵AB与CD相交于点O,
∴
AO=BO.
7、如图所示,在△ABC中,AD平分∠BAC,DE⊥AB于点E,DF⊥AC于点F,试说明AD与EF 的关系.
解:
AD垂直平分EF.
∵AD平分∠BAC,DE⊥AB,DF⊥AC,
∴∠EAD=∠FAD,∠AED=∠AFD=90°.
又∵AD=AD,∴△ADE≌△ADF,
∴AE=AF,DE=DF.
∴A、D均在线段EF的垂直平分线上,
即直线AD垂直平分线段EF.
A
B
C
D
E
F
课堂小结
线段的垂直平分的性质和判定
性质
到线段的两个端点距离相等的点在线段的垂直平分线上
内容
判定
内容
作用
线段的垂直平分线上的点到线段的两个端点的距离相等
作用
见垂直平分线,得线段相等
判断一个点是否在线段的垂直平分线上
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
13.1.2 线段垂直平分线的性质
第1课时 线段的垂直平分线的性质和判定
2020年秋人教版数学八年级上册精品课件
学习目标
1
2
会用尺规过一点作已知直线的垂线.
3
能够运用线段的垂直平分线的性质和判定解决实际问题.(难点)
理解并掌握线段的垂直平分线的性质和判定方法.(重点)
新课导入
某区政府为了方便居民的生活,计划在三个住宅小区 A、B、C 之间修建一个购物中心,试问该购物中心应建于何处,才能使得它到三个小区的距离相等?
A
B
C
知识讲解
1.线段垂直平分线的性质
探究:如图,直线l垂直平分线段 AB,P1,P2,P3,…是l 上的点,请你量一量线段P1A,P1B,P2A,P2B,P3A,P3B 的长,你能发现什么?请猜想点P1,P2,P3,… 到点A 与点B 的距离之间的数量关系.
A
B
l
P1
P2
P3
P1A ____P1B
P2A ____ P2B
P3A ____ P3B
=
=
=
猜想:
点P1,P2,P3,… 到点 A 与点 B 的距离分别相等.
由此你能得到什么结论?
你能验证这一结论吗?
命题:线段垂直平分线上的点和这条线段两个端点的距离相等.
验证:
证明:
∵ l⊥AB,
∴ ∠PCA =∠PCB.
又 AC =CB,PC =PC,
∴ △PCA ≌△PCB(SAS).
∴ PA =PB.
P
A
B
l
C
已知:如图,直线l⊥AB,垂足为C,AC =CB,点P 在l上.
求证:PA =PB.
例1 如图,在△ABC 中,AB=AC=20cm,DE 垂直平分AB,垂足为E,交AC于D,若△DBC 的周长为35cm,则BC 的长为( ).
A.5cm
B.10cm
C.15cm
D.17.5cm
C
解析:
∵△DBC 的周长为BC+BD+CD=35cm,
又∵DE 垂直平分AB,
∴AD=BD,故BC+AD+CD=35cm.
∵AC=AD+DC=20cm,
∴BC=35-20=15(cm). 故选C
总结:利用线段垂直平分线的性质,实现线段之间的相互转化,从而求出未知线段的长.
例2 已知:如图,在 ΔABC 中,边AB,BC 的垂直平分线交于P.
求证:PA=PB=PC.
B
A
C
M
N
M'
N'
P
PA=PB=PC
PB=PC
点P在线段BC的垂直平分线上
PA=PB
点P在线段AB的垂直平分线上
解析:
证明:
∵点P在线段AB的垂直平分线MN上,
∴PA=PB.
同理 PB=PC.
∴PA=PB=PC.
结论:三角形三边垂直平分线交于一点,这一点到三角形三个顶点的距离相等。
现在你能想到方法确定购物中心的位置,使得它到三个小区的距离相等吗?
想一想:如果 PA=PB ,那么点 P 是否在线段 AB 的垂直平分线上呢?
P
A
B
已知:如图,PA =PB.
求证:点P 在线段 AB 的垂直平分线上.
2、线段垂直平分线的判定
探究
证明:
过点P 作AB 的垂线PC,垂足为点C.
则∠PCA =∠PCB =90°.
在Rt△PCA 和Rt△PCB 中,
PA =PB,PC =PC,
∴ Rt△PCA ≌Rt△PCB(HL).
∴ AC =BC.
又 PC⊥AB,
∴ 点P 在线段AB 的垂直平分线上.
P
A
B
C
线段垂直平分线的判定:
与线段两个端点距离相等的点在这条线段的垂直平分线上.
应用格式:
∵ PA =PB,
∴ 点 P 在 AB 的垂直平分线上.
P
A
B
作用:
判断一个点是否在线段的垂直平分线上.
例3 尺规作图:经过已知直线外一点作这条直线的垂线.
A
B
C
D
E
K
已知:直线AB和AB外一点C .
求作:AB的垂线,使它经过点C .
作法:(1)任意取一点K,使点K和点C在AB的两旁.
(2)以点C 为圆心,CK长为半径作弧,交 AB于
点D和点E.
(4)作直线CF.
直线CF就是所求作的垂线.
(3)分别以点D和点E为圆心,大于 DE的长为
半径作弧,两弧相交于点F.
F
例4 已知:如图,点E是∠AOB的平分线上一点,EC⊥OA,ED⊥OB,
垂足分别为C,D,连接CD.
求证:OE是CD的垂直平分线.
A
B
O
E
D
C
证明:
∵OE平分∠AOB,EC⊥OA,ED⊥OB,
∴ DE=CE.
∴ OE是CD的垂直平分线.
又∵OE=OE,
∴Rt△OED≌Rt△OEC.
∴DO=CO.
随堂训练
1、如图所示,AC=AD,BC=BD,则下列说法正确的是( )
A. AB垂直平分CD;
B .CD垂直平分AB ;
C.AB与CD互相垂直平分;
D.CD平分∠ ACB.
A
2、在锐角三角形 ABC 内一点P,满足 PA=PB=PC,则点P是△ABC( )
A、三条角平分线的交点
B、三条中线的交点
C、三条高的交点
D、三边垂直平分线的交点
D
4、下列说法:
① 若点P、E是线段AB的垂直平分线上两点,则EA=EB,PA=PB;
②若PA=PB,EA=EB,则直线PE垂直平分线段AB;
③若PA=PB,则点P必是线段AB的垂直平分线上的点;
④若EA=EB,则经过点E的直线垂直平分线段AB.
其中正确的有 (填序号).
① ② ③
3、已知线段AB,在平面上找到三个点D、E、F,使DA=DB,EA=EB,FA=FB,这样的点的组合共有 种.
无数
5、如图,△ABC中,AB=AC,AB的垂直平分线交AC于E,连接BE,AB+BC=16cm,则△BCE的周长是 cm.
A
B
C
D
E
16
6、已知:如图,点C,D是线段AB外的两点,且AC =BC, AD=BD,
AB与CD相交于点O.
求证:AO=BO.
证明:
∵ AC =BC,AD=BD,
∴
点C和点D在线段AB的垂直平分线上,
∴ CD为线段AB的垂直平分线.
又 ∵AB与CD相交于点O,
∴
AO=BO.
7、如图所示,在△ABC中,AD平分∠BAC,DE⊥AB于点E,DF⊥AC于点F,试说明AD与EF 的关系.
解:
AD垂直平分EF.
∵AD平分∠BAC,DE⊥AB,DF⊥AC,
∴∠EAD=∠FAD,∠AED=∠AFD=90°.
又∵AD=AD,∴△ADE≌△ADF,
∴AE=AF,DE=DF.
∴A、D均在线段EF的垂直平分线上,
即直线AD垂直平分线段EF.
A
B
C
D
E
F
课堂小结
线段的垂直平分的性质和判定
性质
到线段的两个端点距离相等的点在线段的垂直平分线上
内容
判定
内容
作用
线段的垂直平分线上的点到线段的两个端点的距离相等
作用
见垂直平分线,得线段相等
判断一个点是否在线段的垂直平分线上
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
