8.2.3解一元一次不等式
图片预览





文档简介
(共21张PPT)
习居彩
尝试用数学语言表述生活现象
如果设气温为 t ℃,那么
最低气温-1 ℃ 表示为
t≥ -1 ①
t ≤ 8 ②
最高气温8 ℃ 表示为
尝试用数学语言表述生活现象
t≥ -1 ① 一元一次不等式
t ≤ 8 ② 一元一次不等式
一元一次
不等式组
一般地,几个一元一次不等式所组成的不等式组叫做一元一次不等式组。
那么,日照的气温可表示为
-8 -4 -1 0 4 8
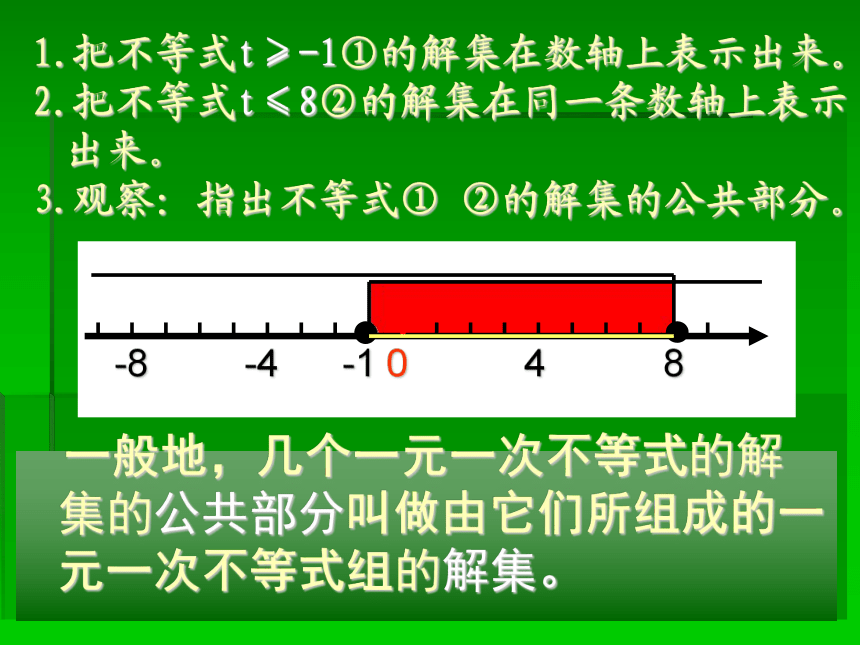
把不等式t≥-1①的解集在数轴上表示出来。
把不等式t≤8②的解集在同一条数轴上表示出来。
观察:指出不等式① ②的解集的公共部分。
一般地,几个一元一次不等式的解集的公共部分叫做由它们所组成的一元一次不等式组的解集。
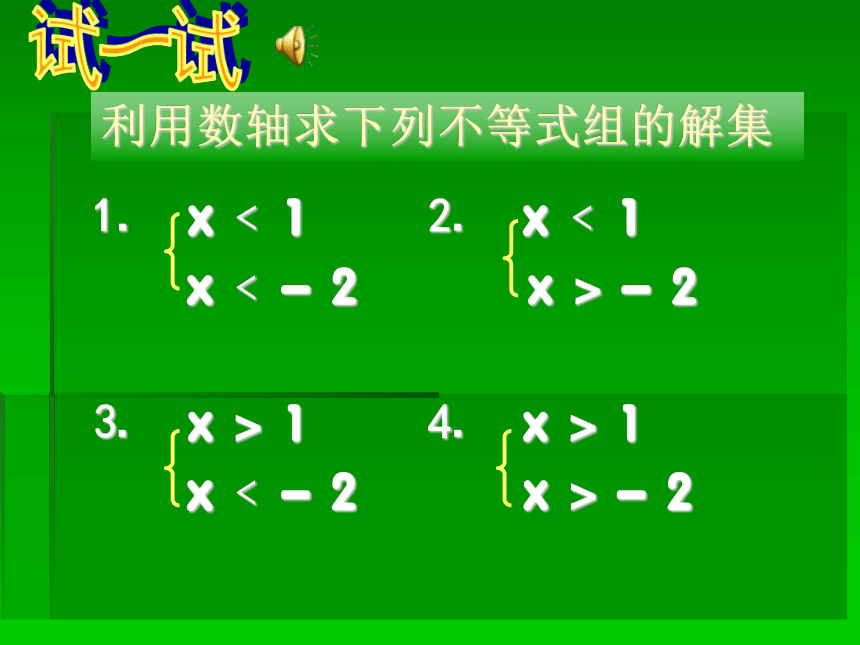
⒈ x﹤1 ⒉ x﹤1
x﹤-2 x>-2
⒊ x>1 ⒋ x>1
x﹤-2 x>-2
利用数轴求下列不等式组的解集
⒈ x﹤1 ⒉ x﹤1
x﹤-2 x>-2
⒊ x>1 ⒋ x>1
x﹤-2 x>-2
利用数轴求下列不等式组的解集
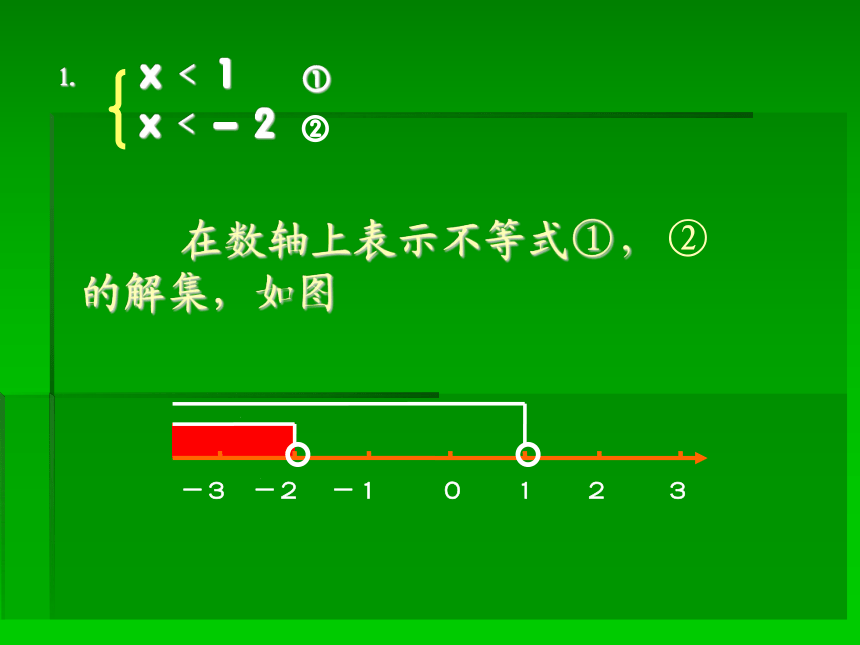
在数轴上表示不等式①,②的解集,如图
⒈ x﹤1 ①
x﹤-2 ②
-3 -2 -1 0 1 2 3
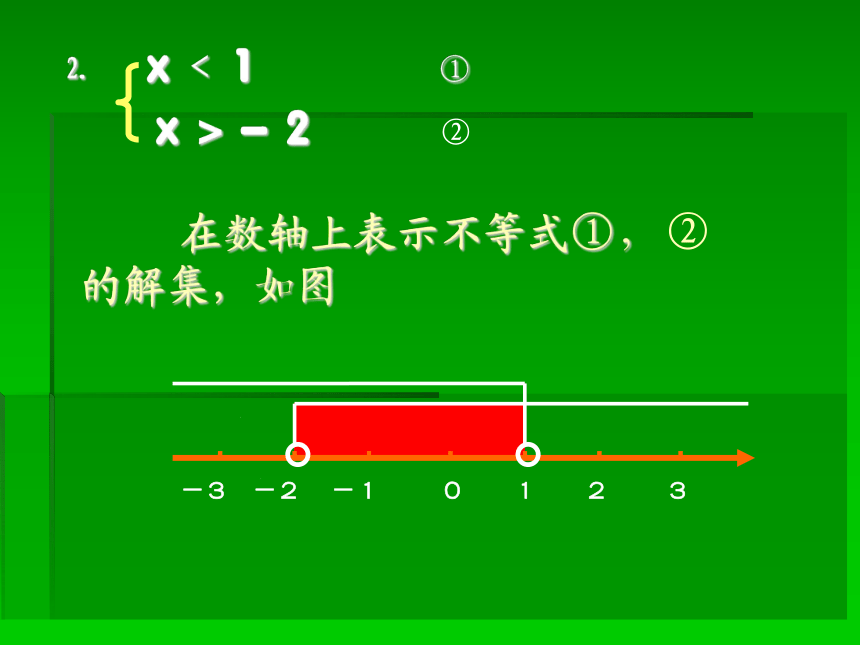
⒉ x﹤1 ①
x>-2 ②
在数轴上表示不等式①,②的解集,如图
-3 -2 -1 0 1 2 3
⒊ x>1 ①
x﹤-2 ②
在数轴上表示不等式①,②的解集,如图
-3 -2 -1 0 1 2 3
⒋ x>1 ①
x>-2 ②
在数轴上表示不等式①,②的解集,如图
-3 -2 -1 0 1 2 3
解:解不等式①,得 x>2
解不等式②,得 x>3
在数轴上表示不等式①,②的解集,如图
所以这个不等式组的解集是 x>3
例1:解不等式组 2x-1>x+1 ①
x+8<4x-1 ②
-1 0 1 2 3
让我们来体验一下探索研究的快乐吧!
请自己设计一个不等式组
(或每小组设计一个)。
尝试解这个不等式组。
例2 解不等式组 2x+3 <5
3x- 2 >4
解:解不等式①,得 x<1.
解不等式②,得 x>2.
在数轴上表示不等式①,②的解集,
这两个不等式的解集没有公共部分,
这时,我们说不等式组无解.
-3 -2 -1 0 1 2 3
例3 解不等式组 5x-2>3(x+1)
x-2≤14-3x
解:解不等式①,得 x >
解不等式②,得 x≤4.
在数轴上表示不等式①,②的解集
所以不等式组的解集是 < x≤4
-1 0 1 2 3 4
分小组共同研究如下问题:
系数化为 1 时要注意什么问题?
在数轴上表示各个不等式的解集时方向与端点如何画?
怎样确定不等式组的解集?
请你试总结一下
解一元一次不等式组的一般步骤:
1.求出这个不等式组中各个不等式的解集。
2.利用数轴求出这些不等式的解集的公共部分。
我们来总结一下这节课所研究的问题
我们一起学习了一元一次不等式组和它的解集的概念。
我们通过自己研究和合作研究,学习了一元一次不等式组的解法步骤。
研究数量关系的问题,有时可以把它转化为图形来研究。
习居彩
尝试用数学语言表述生活现象
如果设气温为 t ℃,那么
最低气温-1 ℃ 表示为
t≥ -1 ①
t ≤ 8 ②
最高气温8 ℃ 表示为
尝试用数学语言表述生活现象
t≥ -1 ① 一元一次不等式
t ≤ 8 ② 一元一次不等式
一元一次
不等式组
一般地,几个一元一次不等式所组成的不等式组叫做一元一次不等式组。
那么,日照的气温可表示为
-8 -4 -1 0 4 8
把不等式t≥-1①的解集在数轴上表示出来。
把不等式t≤8②的解集在同一条数轴上表示出来。
观察:指出不等式① ②的解集的公共部分。
一般地,几个一元一次不等式的解集的公共部分叫做由它们所组成的一元一次不等式组的解集。
⒈ x﹤1 ⒉ x﹤1
x﹤-2 x>-2
⒊ x>1 ⒋ x>1
x﹤-2 x>-2
利用数轴求下列不等式组的解集
⒈ x﹤1 ⒉ x﹤1
x﹤-2 x>-2
⒊ x>1 ⒋ x>1
x﹤-2 x>-2
利用数轴求下列不等式组的解集
在数轴上表示不等式①,②的解集,如图
⒈ x﹤1 ①
x﹤-2 ②
-3 -2 -1 0 1 2 3
⒉ x﹤1 ①
x>-2 ②
在数轴上表示不等式①,②的解集,如图
-3 -2 -1 0 1 2 3
⒊ x>1 ①
x﹤-2 ②
在数轴上表示不等式①,②的解集,如图
-3 -2 -1 0 1 2 3
⒋ x>1 ①
x>-2 ②
在数轴上表示不等式①,②的解集,如图
-3 -2 -1 0 1 2 3
解:解不等式①,得 x>2
解不等式②,得 x>3
在数轴上表示不等式①,②的解集,如图
所以这个不等式组的解集是 x>3
例1:解不等式组 2x-1>x+1 ①
x+8<4x-1 ②
-1 0 1 2 3
让我们来体验一下探索研究的快乐吧!
请自己设计一个不等式组
(或每小组设计一个)。
尝试解这个不等式组。
例2 解不等式组 2x+3 <5
3x- 2 >4
解:解不等式①,得 x<1.
解不等式②,得 x>2.
在数轴上表示不等式①,②的解集,
这两个不等式的解集没有公共部分,
这时,我们说不等式组无解.
-3 -2 -1 0 1 2 3
例3 解不等式组 5x-2>3(x+1)
x-2≤14-3x
解:解不等式①,得 x >
解不等式②,得 x≤4.
在数轴上表示不等式①,②的解集
所以不等式组的解集是 < x≤4
-1 0 1 2 3 4
分小组共同研究如下问题:
系数化为 1 时要注意什么问题?
在数轴上表示各个不等式的解集时方向与端点如何画?
怎样确定不等式组的解集?
请你试总结一下
解一元一次不等式组的一般步骤:
1.求出这个不等式组中各个不等式的解集。
2.利用数轴求出这些不等式的解集的公共部分。
我们来总结一下这节课所研究的问题
我们一起学习了一元一次不等式组和它的解集的概念。
我们通过自己研究和合作研究,学习了一元一次不等式组的解法步骤。
研究数量关系的问题,有时可以把它转化为图形来研究。
