华师大版数学七上 4.6.2 角的运算和比较 课件 (共15张ppt)
文档属性
| 名称 | 华师大版数学七上 4.6.2 角的运算和比较 课件 (共15张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 569.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-21 00:00:00 | ||
图片预览






文档简介
4.6-2角的比较和运算
教学目标
1.使学生通过联想线段大小的比较方法,找到角的大小的比较方法.
2.使学生通过联想线段和、差、倍、分的作法,掌握角的和、差、倍、分的作法和计算.
3.使学生掌握角的平分线的定义以及数学表达式.
4.培养学生类比联想的思维能力和对知识的迁移能力
教学重点、难点
教学重点
角的两种比较方法、角的和、差、倍、分的作法和计算、角的平分线定义
教学难点
角平分线定义的各种数学表达式
(1)在放大镜下,一个角的度数变大了吗?
(2)角的两边的长短与角的大小有关吗?
一、温故知新、引入课题
想一想
同学们,你们有办法进行判断吗?
角的比较:
A
B
C
D
E
F
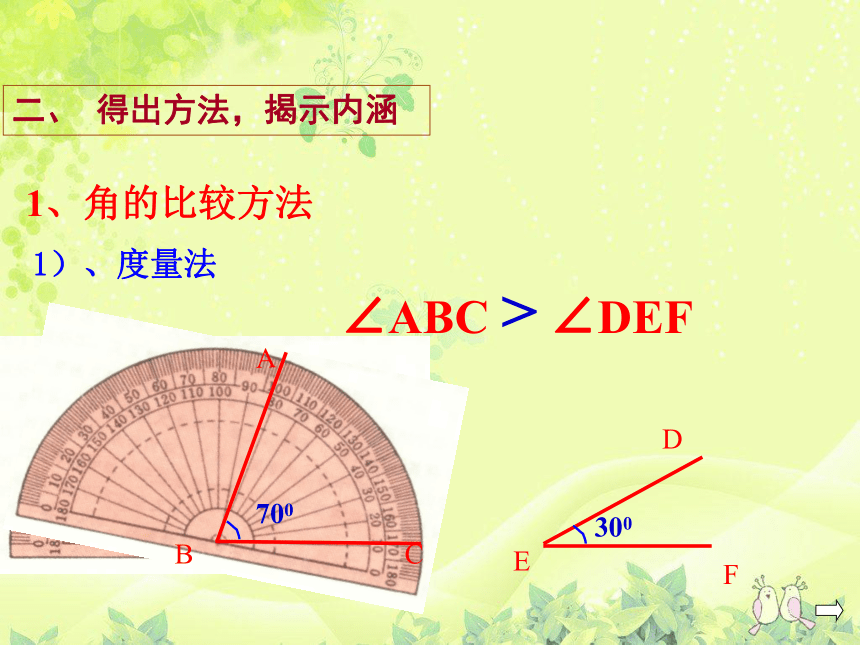
怎样比较∠ABC和∠DEF的大小?
B
C
A
F
E
D
700
300
∠ABC > ∠DEF
1、角的比较方法
1)、度量法
二、??得出方法,揭示内涵
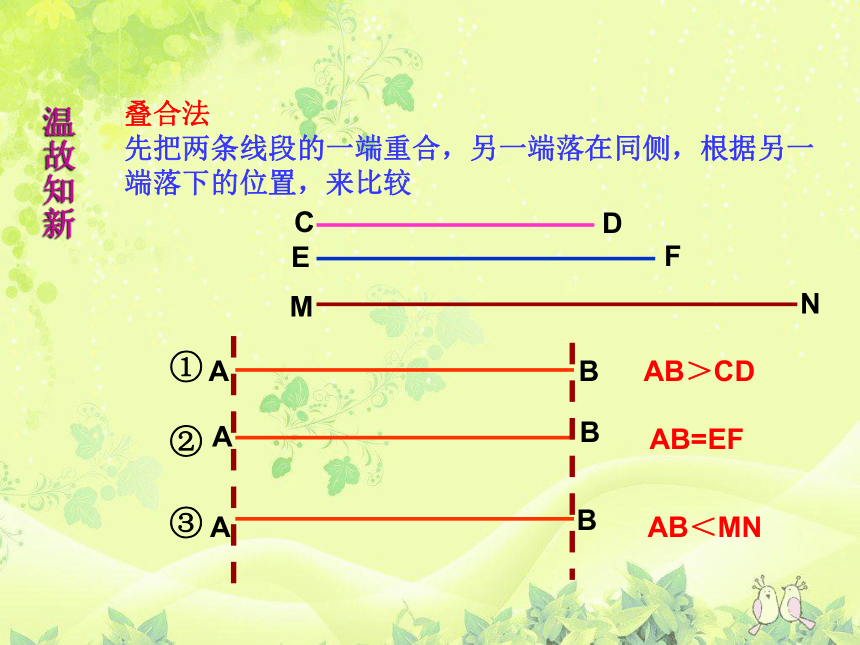
叠合法
先把两条线段的一端重合,另一端落在同侧,根据另一端落下的位置,来比较
①
②
③
A
B
B
A
A
B
C
D
E
F
M
N
AB>CD
AB=EF
AB<MN
温故知新
A
C
B
A
C
B
A
C
B
D
E
F
A
C
B
D
E
F
D
E
F
A
C
B
A
C
B
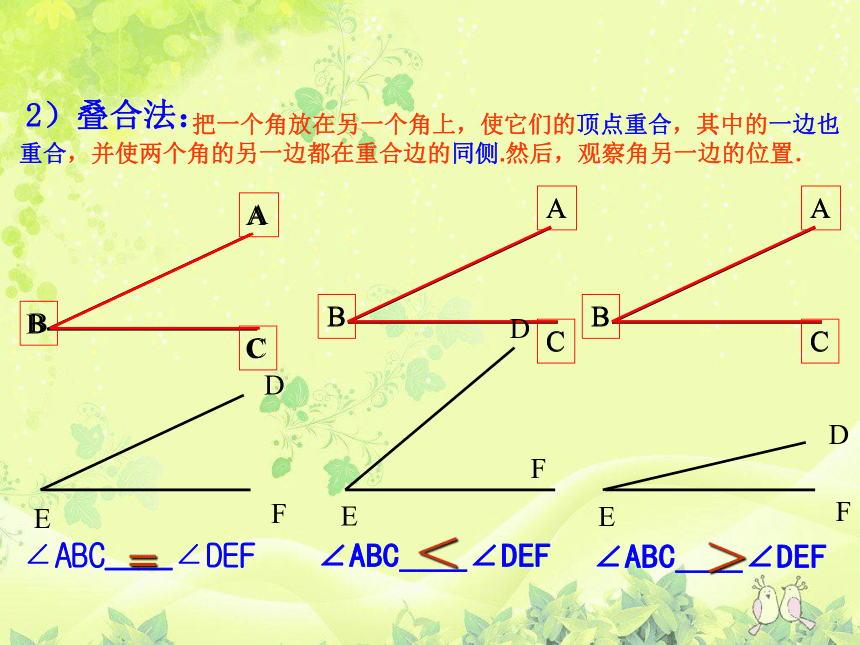
∠ABC____∠DEF
∠ABC____∠DEF
∠ABC____∠DEF
=
<
>
2)叠合法:
把一个角放在另一个角上,使它们的顶点重合,其中的一边也重合,并使两个角的另一边都在重合边的同侧.然后,观察角另一边的位置.
(1)在放大镜下,一个角的度数变大了吗?
(2)角的两边的长短与角的大小有关吗?
结论:角的大小与角的两边张开的大小一致,与所画边的长短无关
2、角的运算
图中共有几个角,它们之间的大小有什么关系?
O
C
B
A
∠AOC ∠AOB ∠BOC
= +
∠AOB = ∠AOC-∠ __
BOC
∠BOC = ∠__ -∠ __
AOC
AOB
D
C
B
A
O
∠AOC =∠AOB + ∠ __
∠BOD = ∠COD+ ∠ __
∠AOC= ∠AOD-∠ __
∠BOD= ∠ __ -∠ __
BOC
BOC
COD
AOB
AOD
填一填
若∠AOC= ,∠BOC= ,则∠AOB=?
A
B
C
O
角的加减运算:
15°、75°、105°、120°、135°、150°、 165 °
30°、45°、60°、90°、
3、角的画法
1)利用三角板可以画出哪些度数的角?
所以∠A O B 就是我们所要作的角.
1
1
1
2)你会利用量角器画一个角等于∠AOB吗?
O
A
B
A
1
O
1
量已知角
画射线
描点
B
1
画射线
对心,对线,读数
对心,对线
2)你会利用量角器画一个角等于∠AOB吗?
O
A
B
A
1
O
1
量已知角
画射线
描点
B
1
所以∠A O B 就是我们所要作的角.
1
1
1
画射线
如果只用圆规和没有刻度的直尺能画
一个角等于已知角吗?
3)用尺规画角
用尺规画角的步骤:
● 以O为圆心,以适当长为半径画弧,交角的两边于C, D两点;
● 画射线EF,以E为圆心,以同样长为半径画弧,交射线EF于G点;
● 以C为圆心,以线段CD长为半径画弧,;
● 画射线EH.
O
A
B
C
D
G
E
F
● 再以点G为圆心,以同样长为半径画弧,交原先的弧交于点H;
H
4、角平分线
将你手中的角对折,使其两边重合,折痕
把这个角分成的两部分是什么图形,你发现它们
的大小有什么关系?
折痕与这个角的两边组成两个角
它们的大小相等 ∠1 =∠2
从一个角的顶点出发,把这个角分成相等的两个角的射线,叫做这个角的平分线
1
2
做一做,想一想
(1)若OB是∠AOC的平分线,那么
∠AOB = ∠ __ = ∠ __
∠AOC =2∠AOB =2∠ __
O
A
C
B
(2)若OB是∠AOC的平分线,OC是∠BOD的平分线,你能从中找出哪些相等的角?
O
A
B
C
D
∠AOB= ∠BOC= ∠COD
∠AOC= ∠BOD
BOC
BOC
AOC
1、填空
例1:如图 O是直线AB上的一点, ∠AOC=53 ° 17 ′求∠BOC的度数
A
O
B
C
分析:(1) AB是直线 , ∠AOB 是什么角?
(2)∠BOC 、 ∠AOB 、 ∠AOC之间有什么关系?
∠AOB是平角,等于180°
∠AOB = ∠BOC + ∠AOC
解: ∠BOC= ∠AOB- ∠AOC=180°- 53° 17′
=126°43′
三 例题示范,初步运用
四、分层练习,形成能力
1、看图填空:
1)、如图(1)若∠AOC=32°,∠BOC=43°则∠AOB=
若已知 ∠AOB = 68 ° ∠BOC=40°则∠AOC=
2)如图(2)若∠AOC=90°, ∠BOD=90°那么
图中相等的角是
A
C
B
D
C
B
A
图(1)
图(2)
75 °
28°
∠AOC= ∠BOD
∠AOB= ∠COD
2、如图,OB是∠AOC的平分线,
OE是∠COD的平分线,
A
C
B
O
E
D
(1)若∠AOC=50°, ∠COD=80°,
那么∠BOE是多少度?
(2)若∠AOD=130°, 那么∠BOE是多少度?
(3)若∠BOE=60°, 那么∠AOD是多少度?
(4) 由上可知: ∠BOE=_____∠AOD.
1
2
3、 已知射线OA,若从点O再引两条射线OB和OC,∠AOB=60°,∠BOC=20 ° ,求∠AOC的度数。
解:如图(1),
∠AOC =∠AOB+∠BOC=80 °
O
C
B
A
(1)
C
B
A
O
(2)
如图(2),
∠AOC =∠AOB-∠BOC=40 °
已知:∠AOC、∠BOC有一条公共边OC,如果∠AOC=60°,∠BOC=40°, OM、ON分别是∠AOC、∠BOC的角平分线,求∠MON的度数。
O
A
B
C
M
N
O
A
B
C
M
N
能力拓展
这节课,我的收获是---
五、回顾小结,突出重点
学习的内容有三个:
(1)比较角的大小.
(2)角的和、差、倍、分.
(3)角平分线的概念.
本节课里我的收获是……
1.课本P159页,习题4.6 4,5,
2.预习课本P157—P159
六、布置作业,引导预习
教学目标
1.使学生通过联想线段大小的比较方法,找到角的大小的比较方法.
2.使学生通过联想线段和、差、倍、分的作法,掌握角的和、差、倍、分的作法和计算.
3.使学生掌握角的平分线的定义以及数学表达式.
4.培养学生类比联想的思维能力和对知识的迁移能力
教学重点、难点
教学重点
角的两种比较方法、角的和、差、倍、分的作法和计算、角的平分线定义
教学难点
角平分线定义的各种数学表达式
(1)在放大镜下,一个角的度数变大了吗?
(2)角的两边的长短与角的大小有关吗?
一、温故知新、引入课题
想一想
同学们,你们有办法进行判断吗?
角的比较:
A
B
C
D
E
F
怎样比较∠ABC和∠DEF的大小?
B
C
A
F
E
D
700
300
∠ABC > ∠DEF
1、角的比较方法
1)、度量法
二、??得出方法,揭示内涵
叠合法
先把两条线段的一端重合,另一端落在同侧,根据另一端落下的位置,来比较
①
②
③
A
B
B
A
A
B
C
D
E
F
M
N
AB>CD
AB=EF
AB<MN
温故知新
A
C
B
A
C
B
A
C
B
D
E
F
A
C
B
D
E
F
D
E
F
A
C
B
A
C
B
∠ABC____∠DEF
∠ABC____∠DEF
∠ABC____∠DEF
=
<
>
2)叠合法:
把一个角放在另一个角上,使它们的顶点重合,其中的一边也重合,并使两个角的另一边都在重合边的同侧.然后,观察角另一边的位置.
(1)在放大镜下,一个角的度数变大了吗?
(2)角的两边的长短与角的大小有关吗?
结论:角的大小与角的两边张开的大小一致,与所画边的长短无关
2、角的运算
图中共有几个角,它们之间的大小有什么关系?
O
C
B
A
∠AOC ∠AOB ∠BOC
= +
∠AOB = ∠AOC-∠ __
BOC
∠BOC = ∠__ -∠ __
AOC
AOB
D
C
B
A
O
∠AOC =∠AOB + ∠ __
∠BOD = ∠COD+ ∠ __
∠AOC= ∠AOD-∠ __
∠BOD= ∠ __ -∠ __
BOC
BOC
COD
AOB
AOD
填一填
若∠AOC= ,∠BOC= ,则∠AOB=?
A
B
C
O
角的加减运算:
15°、75°、105°、120°、135°、150°、 165 °
30°、45°、60°、90°、
3、角的画法
1)利用三角板可以画出哪些度数的角?
所以∠A O B 就是我们所要作的角.
1
1
1
2)你会利用量角器画一个角等于∠AOB吗?
O
A
B
A
1
O
1
量已知角
画射线
描点
B
1
画射线
对心,对线,读数
对心,对线
2)你会利用量角器画一个角等于∠AOB吗?
O
A
B
A
1
O
1
量已知角
画射线
描点
B
1
所以∠A O B 就是我们所要作的角.
1
1
1
画射线
如果只用圆规和没有刻度的直尺能画
一个角等于已知角吗?
3)用尺规画角
用尺规画角的步骤:
● 以O为圆心,以适当长为半径画弧,交角的两边于C, D两点;
● 画射线EF,以E为圆心,以同样长为半径画弧,交射线EF于G点;
● 以C为圆心,以线段CD长为半径画弧,;
● 画射线EH.
O
A
B
C
D
G
E
F
● 再以点G为圆心,以同样长为半径画弧,交原先的弧交于点H;
H
4、角平分线
将你手中的角对折,使其两边重合,折痕
把这个角分成的两部分是什么图形,你发现它们
的大小有什么关系?
折痕与这个角的两边组成两个角
它们的大小相等 ∠1 =∠2
从一个角的顶点出发,把这个角分成相等的两个角的射线,叫做这个角的平分线
1
2
做一做,想一想
(1)若OB是∠AOC的平分线,那么
∠AOB = ∠ __ = ∠ __
∠AOC =2∠AOB =2∠ __
O
A
C
B
(2)若OB是∠AOC的平分线,OC是∠BOD的平分线,你能从中找出哪些相等的角?
O
A
B
C
D
∠AOB= ∠BOC= ∠COD
∠AOC= ∠BOD
BOC
BOC
AOC
1、填空
例1:如图 O是直线AB上的一点, ∠AOC=53 ° 17 ′求∠BOC的度数
A
O
B
C
分析:(1) AB是直线 , ∠AOB 是什么角?
(2)∠BOC 、 ∠AOB 、 ∠AOC之间有什么关系?
∠AOB是平角,等于180°
∠AOB = ∠BOC + ∠AOC
解: ∠BOC= ∠AOB- ∠AOC=180°- 53° 17′
=126°43′
三 例题示范,初步运用
四、分层练习,形成能力
1、看图填空:
1)、如图(1)若∠AOC=32°,∠BOC=43°则∠AOB=
若已知 ∠AOB = 68 ° ∠BOC=40°则∠AOC=
2)如图(2)若∠AOC=90°, ∠BOD=90°那么
图中相等的角是
A
C
B
D
C
B
A
图(1)
图(2)
75 °
28°
∠AOC= ∠BOD
∠AOB= ∠COD
2、如图,OB是∠AOC的平分线,
OE是∠COD的平分线,
A
C
B
O
E
D
(1)若∠AOC=50°, ∠COD=80°,
那么∠BOE是多少度?
(2)若∠AOD=130°, 那么∠BOE是多少度?
(3)若∠BOE=60°, 那么∠AOD是多少度?
(4) 由上可知: ∠BOE=_____∠AOD.
1
2
3、 已知射线OA,若从点O再引两条射线OB和OC,∠AOB=60°,∠BOC=20 ° ,求∠AOC的度数。
解:如图(1),
∠AOC =∠AOB+∠BOC=80 °
O
C
B
A
(1)
C
B
A
O
(2)
如图(2),
∠AOC =∠AOB-∠BOC=40 °
已知:∠AOC、∠BOC有一条公共边OC,如果∠AOC=60°,∠BOC=40°, OM、ON分别是∠AOC、∠BOC的角平分线,求∠MON的度数。
O
A
B
C
M
N
O
A
B
C
M
N
能力拓展
这节课,我的收获是---
五、回顾小结,突出重点
学习的内容有三个:
(1)比较角的大小.
(2)角的和、差、倍、分.
(3)角平分线的概念.
本节课里我的收获是……
1.课本P159页,习题4.6 4,5,
2.预习课本P157—P159
六、布置作业,引导预习
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
