三角形全等的判定复习课
图片预览



文档简介
(共20张PPT)
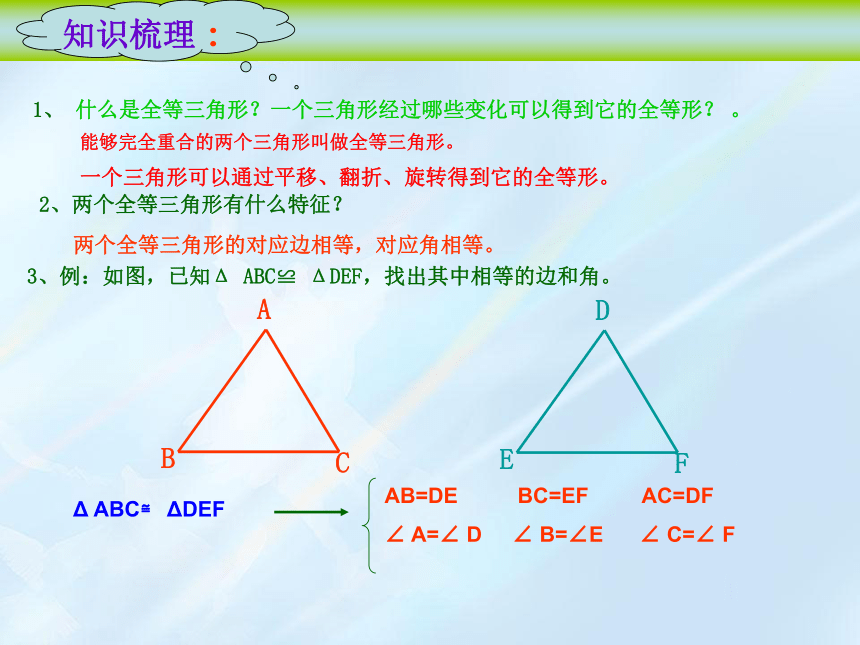
1、 什么是全等三角形?一个三角形经过哪些变化可以得到它的全等形? 。
能够完全重合的两个三角形叫做全等三角形。
2、两个全等三角形有什么特征?
两个全等三角形的对应边相等,对应角相等。
3、例:如图,已知Δ ABC≌ ΔDEF,找出其中相等的边和角。
A
B
C
D
E
F
Δ ABC≌ ΔDEF
AB=DE BC=EF AC=DF
∠ A=∠ D ∠ B=∠E ∠ C=∠ F
知识梳理:
一个三角形可以通过平移、翻折、旋转得到它的全等形。
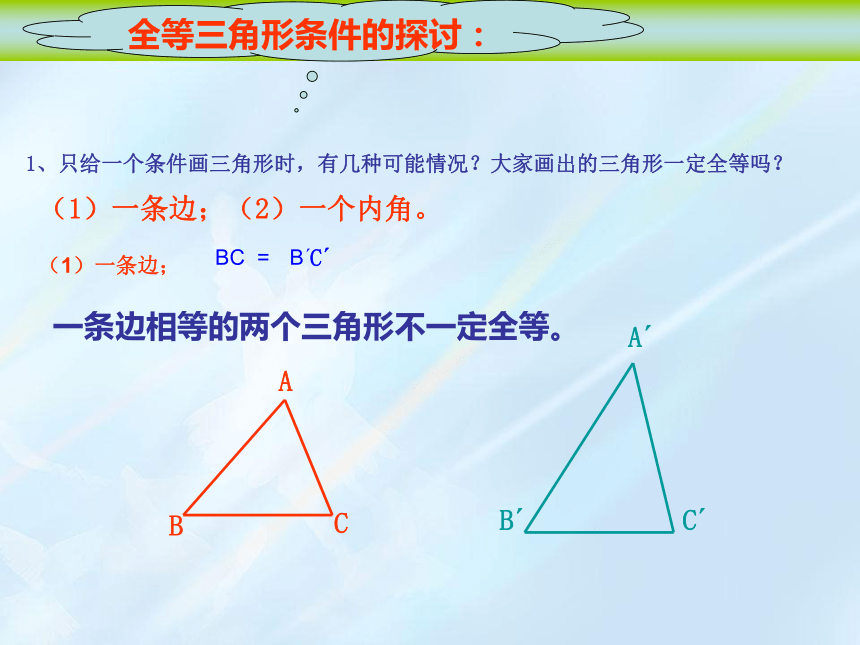
1、只给一个条件画三角形时,有几种可能情况?大家画出的三角形一定全等吗?
(1)一条边;
A
B
C
一条边相等的两个三角形不一定全等。
(1)一条边;(2)一个内角。
全等三角形条件的探讨:
BC =
B
C
A
B
C
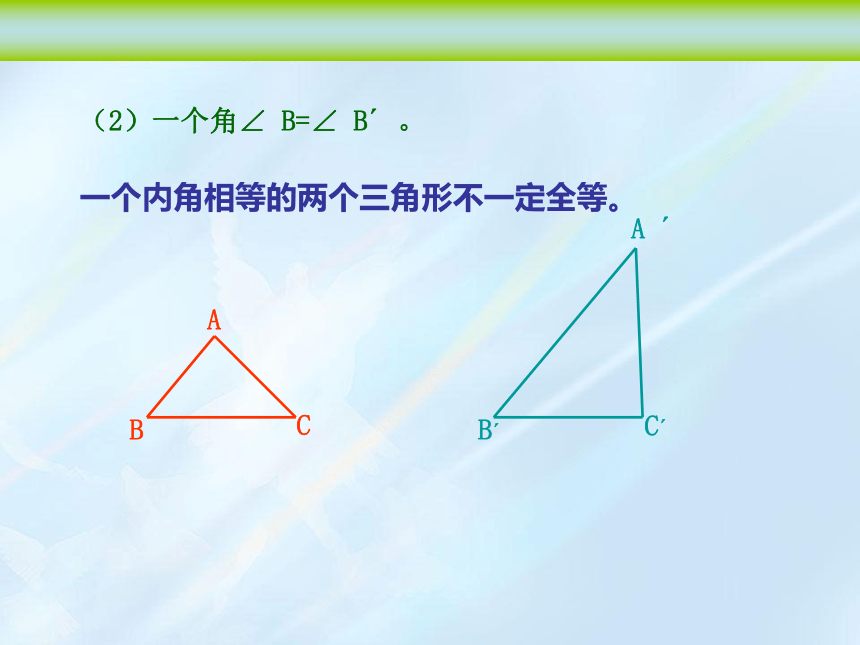
(2)一个角∠ B=∠ B 。
A
B
C
A
B
C
一个内角相等的两个三角形不一定全等。
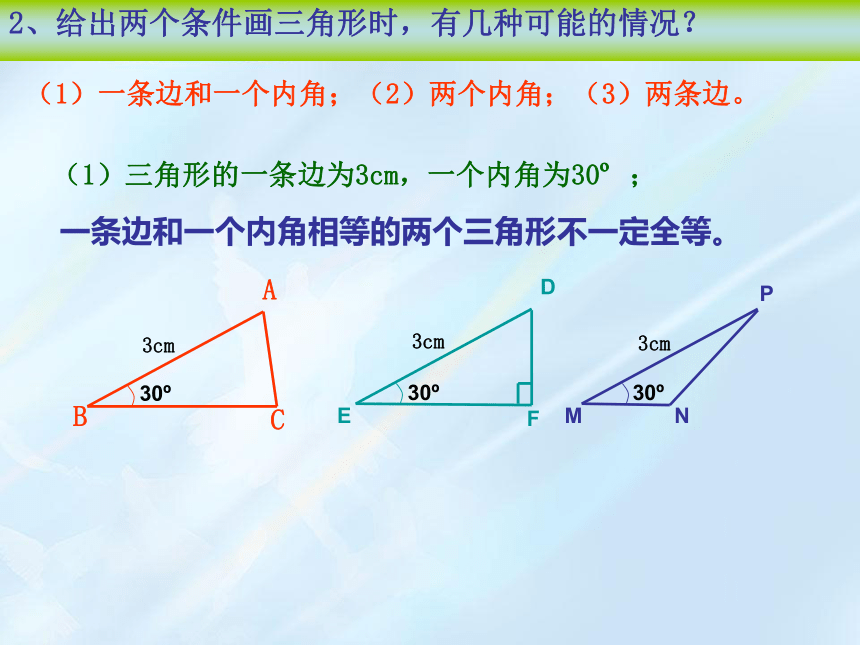
(1)三角形的一条边为3cm,一个内角为30 ;
A
B
C
3cm
30
3cm
30
D
F
E
3cm
30
P
N
M
一条边和一个内角相等的两个三角形不一定全等。
(1)一条边和一个内角;(2)两个内角;(3)两条边。
2、给出两个条件画三角形时,有几种可能的情况?
(2)三角形两内角分别为30 和50 ;
A
B
C
30
50
D
E
F
30
50
两个内角相等的两个三角形不一定全等。
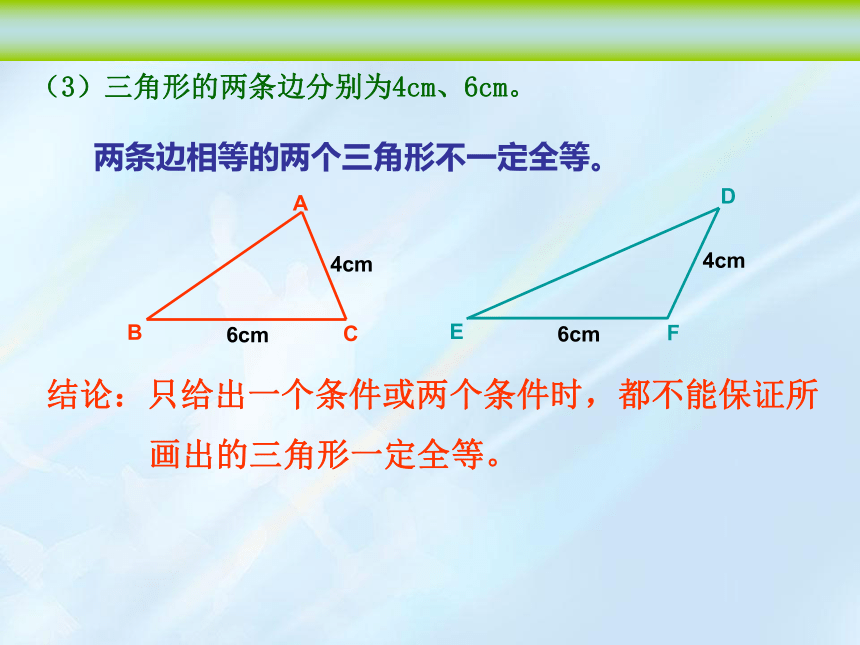
(3)三角形的两条边分别为4cm、6cm。
A
B
C
6cm
4cm
D
E
F
6cm
4cm
两条边相等的两个三角形不一定全等。
结论:只给出一个条件或两个条件时,都不能保证所
画出的三角形一定全等。
如果给出三个条件画三角形,有几种可能的情况?
1、三条边;(SSS)
2、三个角;(AAA)
3、两边一角;(SAS SSA)
4、两角一边。(ASA AAS)
有四种可能:
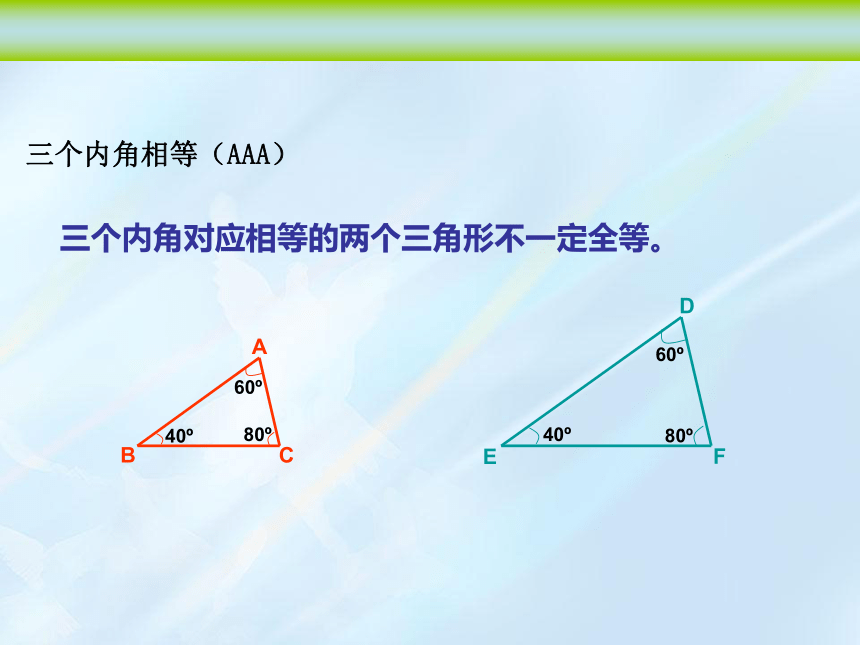
三个内角相等(AAA)
40
60
80
A
B
C
D
E
F
40
80
60
三个内角对应相等的两个三角形不一定全等。
两边和其中一边的对角对应相等的两个三角形不一定全等
两边和其中一边的对角(SSA)
如图:在△ABD和△ABC中
但△ABC与△ABD明显不全等
AC=AD
AB=AB
∠B=∠B
三角形全等的判定
一、边边边 (SSS)
二、边角边 (SAS)
三、角边角 (ASA)
四、角角边 ( AAS)
五、直角边和斜边 (HL)
:利用全等三角形证明线段(或角)相等
全等三角形的应用
例1:如图,直线AC、 BD交于点O,OA=OC OB=OD 直线EF过点O且分别交AB、 CD于E、F
求证:OE=OF
在△AOB和△COD中
OB=OD
∠AOB=∠COD
OA=OC
∴△AOB≌△COD (SAS)
∴∠B=∠D (全等三角形的对应角相等)
在△BOE和△DOF中
∠B=∠D
OB=OD
∠BOE=∠COF
∴△BOE≌△DOF (ASA)
∴OE=OF (全等三角形的对应边相等)
证明
AB=DC
AC=DB
BC=CB
证明:
在△ABC和△DCB中
如图:AB=DC,AC=DB
求证:∠ABO=∠DCO
∴ △ABC△DCB
(SSS)
∴ ∠A=∠D (全等三角形的对应角相等)
在△AOB和△DOC中
∠A=∠D
∠AOB=∠DOC
AB=CD
∴ △AOB≌△DOC
(AAS)
∴ ∠ABO=∠DCO (全等三角形的对应角相等)
在今后的学习中,如果要证明线段相等或角相等,我们首先要想到利用三角形全等这个重要途径。
巩固练习:
如图:AC⊥BC AD⊥BD ,AD=BC CE⊥AB DF⊥AB,垂足分别为E、F,求证:CE=DF
分析:
由已知可推出△ABC≌△BAD
要证CE=DF,需证△ACE≌△ADF,所缺条件可由△ABC≌△BAD推出
二:利用全等三角形证明线的垂直关系
证明:
例:如图:BF是Rt△ABC的角平分线,∠ACB=90°,CD是高,BF与CD交于点E,EG∥AC交AB于G
求证:FG⊥AB
∵BF平分∠ABC
∴∠1=∠2
∵CD⊥AB
∴∠3+∠ABC=90°
又∵∠ACB=90°
∴∠A+∠ABC=90°
∴∠3=∠A
又∵EG∥AC
∴∠A=∠4
∴∠3=∠4
在△BEG与△BEC中
∠1=∠2
∠3=∠4
BE=BE
∴△BEG≌△BEC
(AAS)
∴BG=BC (全等三角形的对应边相等)
在△BFG与△BFC中
BG=BC
∠1=∠2
BF=BF
∴△BFG≌△BFC (SAS)
∴∠FGB=∠FCB=90°(全等三角形的对应角相等)
∴FG⊥AB
巩固练习:
如图:△ABC中,AD平分∠BAC,DE、DF分别垂直于AB、AC,垂足为E、F,AD、EF交于点H
求证:AD⊥EF
三、利用全等三角形证明线段的和差问题
例:在Rt△ABC中,AB=AC,∠BAC=90°,过点A的任意直线AN,BD⊥AN于D,CE⊥AN于E
求证:DE=BD-CE
证明:
∵∠BAC=90°
∴∠1+∠2=90°
∵BD⊥AN
∴∠2+∠3=90°
∴∠1=∠3
又∵CE⊥AN
∴∠ADB=∠AEC=90°
在△ADB和△ACE中
∠1=∠3
∠ADB=∠ACE
AB=AC
∴△ADB≌△ACE
(AAS)
∴AD=CE BD=AE (全等三角形的对应边相等)
∵DE=AE-AD
∴DE=BD-CE
1:个人小结:谈谈你的收获
2:作业
1、 什么是全等三角形?一个三角形经过哪些变化可以得到它的全等形? 。
能够完全重合的两个三角形叫做全等三角形。
2、两个全等三角形有什么特征?
两个全等三角形的对应边相等,对应角相等。
3、例:如图,已知Δ ABC≌ ΔDEF,找出其中相等的边和角。
A
B
C
D
E
F
Δ ABC≌ ΔDEF
AB=DE BC=EF AC=DF
∠ A=∠ D ∠ B=∠E ∠ C=∠ F
知识梳理:
一个三角形可以通过平移、翻折、旋转得到它的全等形。
1、只给一个条件画三角形时,有几种可能情况?大家画出的三角形一定全等吗?
(1)一条边;
A
B
C
一条边相等的两个三角形不一定全等。
(1)一条边;(2)一个内角。
全等三角形条件的探讨:
BC =
B
C
A
B
C
(2)一个角∠ B=∠ B 。
A
B
C
A
B
C
一个内角相等的两个三角形不一定全等。
(1)三角形的一条边为3cm,一个内角为30 ;
A
B
C
3cm
30
3cm
30
D
F
E
3cm
30
P
N
M
一条边和一个内角相等的两个三角形不一定全等。
(1)一条边和一个内角;(2)两个内角;(3)两条边。
2、给出两个条件画三角形时,有几种可能的情况?
(2)三角形两内角分别为30 和50 ;
A
B
C
30
50
D
E
F
30
50
两个内角相等的两个三角形不一定全等。
(3)三角形的两条边分别为4cm、6cm。
A
B
C
6cm
4cm
D
E
F
6cm
4cm
两条边相等的两个三角形不一定全等。
结论:只给出一个条件或两个条件时,都不能保证所
画出的三角形一定全等。
如果给出三个条件画三角形,有几种可能的情况?
1、三条边;(SSS)
2、三个角;(AAA)
3、两边一角;(SAS SSA)
4、两角一边。(ASA AAS)
有四种可能:
三个内角相等(AAA)
40
60
80
A
B
C
D
E
F
40
80
60
三个内角对应相等的两个三角形不一定全等。
两边和其中一边的对角对应相等的两个三角形不一定全等
两边和其中一边的对角(SSA)
如图:在△ABD和△ABC中
但△ABC与△ABD明显不全等
AC=AD
AB=AB
∠B=∠B
三角形全等的判定
一、边边边 (SSS)
二、边角边 (SAS)
三、角边角 (ASA)
四、角角边 ( AAS)
五、直角边和斜边 (HL)
:利用全等三角形证明线段(或角)相等
全等三角形的应用
例1:如图,直线AC、 BD交于点O,OA=OC OB=OD 直线EF过点O且分别交AB、 CD于E、F
求证:OE=OF
在△AOB和△COD中
OB=OD
∠AOB=∠COD
OA=OC
∴△AOB≌△COD (SAS)
∴∠B=∠D (全等三角形的对应角相等)
在△BOE和△DOF中
∠B=∠D
OB=OD
∠BOE=∠COF
∴△BOE≌△DOF (ASA)
∴OE=OF (全等三角形的对应边相等)
证明
AB=DC
AC=DB
BC=CB
证明:
在△ABC和△DCB中
如图:AB=DC,AC=DB
求证:∠ABO=∠DCO
∴ △ABC△DCB
(SSS)
∴ ∠A=∠D (全等三角形的对应角相等)
在△AOB和△DOC中
∠A=∠D
∠AOB=∠DOC
AB=CD
∴ △AOB≌△DOC
(AAS)
∴ ∠ABO=∠DCO (全等三角形的对应角相等)
在今后的学习中,如果要证明线段相等或角相等,我们首先要想到利用三角形全等这个重要途径。
巩固练习:
如图:AC⊥BC AD⊥BD ,AD=BC CE⊥AB DF⊥AB,垂足分别为E、F,求证:CE=DF
分析:
由已知可推出△ABC≌△BAD
要证CE=DF,需证△ACE≌△ADF,所缺条件可由△ABC≌△BAD推出
二:利用全等三角形证明线的垂直关系
证明:
例:如图:BF是Rt△ABC的角平分线,∠ACB=90°,CD是高,BF与CD交于点E,EG∥AC交AB于G
求证:FG⊥AB
∵BF平分∠ABC
∴∠1=∠2
∵CD⊥AB
∴∠3+∠ABC=90°
又∵∠ACB=90°
∴∠A+∠ABC=90°
∴∠3=∠A
又∵EG∥AC
∴∠A=∠4
∴∠3=∠4
在△BEG与△BEC中
∠1=∠2
∠3=∠4
BE=BE
∴△BEG≌△BEC
(AAS)
∴BG=BC (全等三角形的对应边相等)
在△BFG与△BFC中
BG=BC
∠1=∠2
BF=BF
∴△BFG≌△BFC (SAS)
∴∠FGB=∠FCB=90°(全等三角形的对应角相等)
∴FG⊥AB
巩固练习:
如图:△ABC中,AD平分∠BAC,DE、DF分别垂直于AB、AC,垂足为E、F,AD、EF交于点H
求证:AD⊥EF
三、利用全等三角形证明线段的和差问题
例:在Rt△ABC中,AB=AC,∠BAC=90°,过点A的任意直线AN,BD⊥AN于D,CE⊥AN于E
求证:DE=BD-CE
证明:
∵∠BAC=90°
∴∠1+∠2=90°
∵BD⊥AN
∴∠2+∠3=90°
∴∠1=∠3
又∵CE⊥AN
∴∠ADB=∠AEC=90°
在△ADB和△ACE中
∠1=∠3
∠ADB=∠ACE
AB=AC
∴△ADB≌△ACE
(AAS)
∴AD=CE BD=AE (全等三角形的对应边相等)
∵DE=AE-AD
∴DE=BD-CE
1:个人小结:谈谈你的收获
2:作业
