人教版数学七年级上册1.5.1 乘方(1)课件(共22张PPT)
文档属性
| 名称 | 人教版数学七年级上册1.5.1 乘方(1)课件(共22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-21 18:13:33 | ||
图片预览






文档简介
人教版 七上
1.5.1 乘方(1)
你吃过拉面吗?拉面是把一根面条对折成2根拉开,再对折成4根…,依次这样进行对折10次是多少根面条?128根时对折多少次?
解:210=1024(根).27=128,
所以对折10次是1024根,128根时对折7次.
新知导入
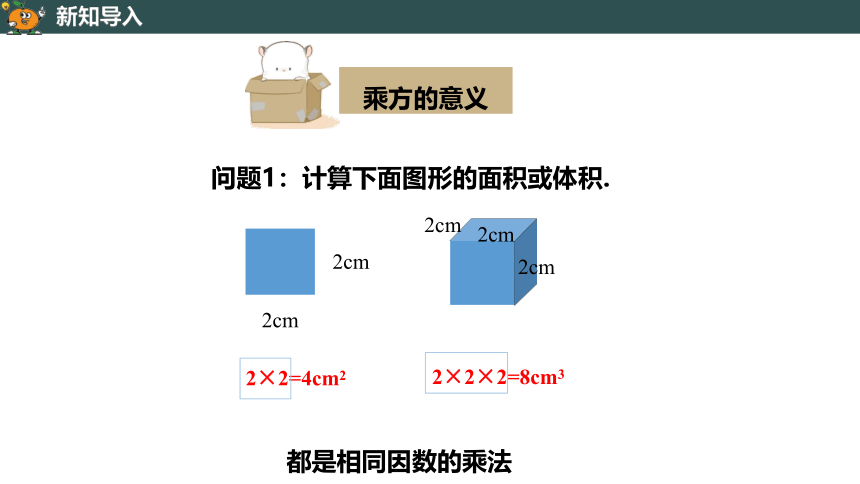
问题1:计算下面图形的面积或体积.
2cm
2cm
2×2=4cm2
2cm
2cm
2cm
2×2×2=8cm3
都是相同因数的乘法
乘方的意义
新知导入
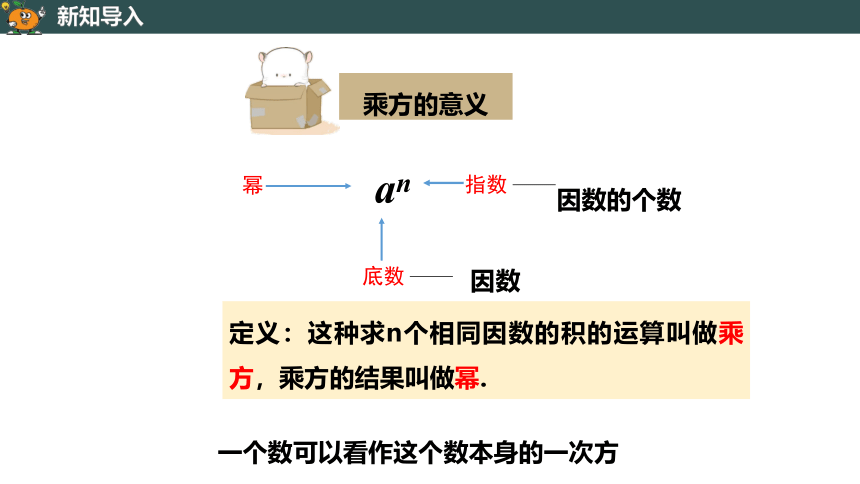
幂
指数
因数的个数
底数
因数
an
定义:这种求n个相同因数的积的运算叫做乘方,乘方的结果叫做幂.
一个数可以看作这个数本身的一次方
乘方的意义
新知导入
填空:
记作:___________,读作:________________
的六次方
记作:___________,读作:________________
-24
2的四次方的相反数
想一想:(-2)4与-24一样吗?为什么?
练习1
填空:
(1)在94中,底数是______, 指数是______,
读作: ______________或_________________.
9
4
9的四次方
9的四次幂
提示:一个数可以看作这个数本身的一次方.
(2)在5中,底数是______, 指数是______,
5
1
5=51
指数1通常省略不写
练习2
例1 计算:
(1) (-4)3; (2) (-2)4; (3) .
(2) (-2)4 =(-2)×(-2)×(-2)×(-2)=16;
(1) (-4)3 =(-4)×(-4)×(-4)=-64;
解:
如何进行乘方运算呢?
表示3个-4相乘.
乘方运算转化为乘法运算.
例题讲解
问题1:从前面的计算中你能发现什么规律?
当指数是____数时,负数的幂是_____数;
(-4)3=(-4)×(-4)×(-4)=-64;
(-2)4=(-2)×(-2)×(-2)×(-2)=16;
当指数是____数时,负数的幂是_____数;
正
奇
负
偶
归纳
根据有理数乘法法则可以得出:
负数的奇次幂是负数,负数的偶次幂是正数;
正数的任何次幂都是正数,
0的任何正整数次幂都是0.
归纳
例2 用计算器计算(-8)5和(-3)6.
解:用带符号键 的计算器.
(-)
=
)
(-)
(
<
8
5
显示:(-8) 5
<
-32768.
=
)
(-)
(
<
3
6
显示:(-3) 6
<
所以(-8)5=-32768,(-3)6=729.
例题讲解
要点1 有理数的乘方的意义
求n个相同因数的 的运算,叫做乘方.乘方的结果叫做幂.在an中,a叫做 ,n叫做 .当an看作a的运算时,读作“ ”,当an看作a的n次方的结果时,也可读作“ ”.
?
积
底数
指数
a的n次方
a的n次幂
课后练习
要点2 有理数乘方的运算
1. 正数的任何次幂都是 ;负数的奇次幂是 .负数的偶次幂是 ;0的任何正整数次幂都是 .
2. 有理数乘方的性质是确定乘方结果的 ,最终的结果还要结合乘方的意义进行计算.
要点3 利用计算器计算有理数的乘方
用计算器计算时,要弄清计算器的每个按键的作用,结合有理数运算的顺序,进行计算.
正数
负数
正数
0
符号
课后练习
1. 下列各组数中:
①-52与(-5)2;②(-3)3与-33;③-(-0.3)5与0.35;④0100与0200;⑤(-1)3与(-1)2,相等的共有( )
A. 1组 B. 2组 C. 3组 D. 4组
C
课后练习
2.计算:
解:
课后练习
3.当n是正整数时,(-1)2n+1-(-1)2n的值是( )
A.2 B.-2 C.0 D.2或-2
B
课后练习
4.a是任意有理数,下列说法正确的是( )
A.(a+1)2的值总是正数
B.a2+1的值总是正数
C.-(a+1)2的值总是负数
D.a2+1的值中最大的是1
B
课后练习
解:
课后练习
6.规定“☆”是一种运算符号,且a☆b=ab-ba,
例如:2☆3=23-32=8-9=-1,
试计算4☆(3☆2)的值.
4☆(3☆2)=4☆(32-23)
=4☆1
=41-14
=3
解:
所以4☆(3☆2)的值是3.
课后练习
7. 小明在电脑上设计了一个有理数运算的程序:输入a,#键,再输入b,得到运算a#b=a2-b2-2ab,求(-2)#3的值.
解:(-2)#3=(-2)2-32-2×(-2)×3=7.
课后练习
1.求几个相同因数的积的运算,叫做乘方.
2.乘方的符号法则:
(1)正数的任何次幂都是正数
(2)负数的奇次幂是负数,负数的偶次幂是正数
(3)零的正整数次幂都是零
幂
指数
底数
课堂总结
教材练习题1—3题.
课后作业
谢
谢
观
看
1.5.1 乘方(1)
你吃过拉面吗?拉面是把一根面条对折成2根拉开,再对折成4根…,依次这样进行对折10次是多少根面条?128根时对折多少次?
解:210=1024(根).27=128,
所以对折10次是1024根,128根时对折7次.
新知导入
问题1:计算下面图形的面积或体积.
2cm
2cm
2×2=4cm2
2cm
2cm
2cm
2×2×2=8cm3
都是相同因数的乘法
乘方的意义
新知导入
幂
指数
因数的个数
底数
因数
an
定义:这种求n个相同因数的积的运算叫做乘方,乘方的结果叫做幂.
一个数可以看作这个数本身的一次方
乘方的意义
新知导入
填空:
记作:___________,读作:________________
的六次方
记作:___________,读作:________________
-24
2的四次方的相反数
想一想:(-2)4与-24一样吗?为什么?
练习1
填空:
(1)在94中,底数是______, 指数是______,
读作: ______________或_________________.
9
4
9的四次方
9的四次幂
提示:一个数可以看作这个数本身的一次方.
(2)在5中,底数是______, 指数是______,
5
1
5=51
指数1通常省略不写
练习2
例1 计算:
(1) (-4)3; (2) (-2)4; (3) .
(2) (-2)4 =(-2)×(-2)×(-2)×(-2)=16;
(1) (-4)3 =(-4)×(-4)×(-4)=-64;
解:
如何进行乘方运算呢?
表示3个-4相乘.
乘方运算转化为乘法运算.
例题讲解
问题1:从前面的计算中你能发现什么规律?
当指数是____数时,负数的幂是_____数;
(-4)3=(-4)×(-4)×(-4)=-64;
(-2)4=(-2)×(-2)×(-2)×(-2)=16;
当指数是____数时,负数的幂是_____数;
正
奇
负
偶
归纳
根据有理数乘法法则可以得出:
负数的奇次幂是负数,负数的偶次幂是正数;
正数的任何次幂都是正数,
0的任何正整数次幂都是0.
归纳
例2 用计算器计算(-8)5和(-3)6.
解:用带符号键 的计算器.
(-)
=
)
(-)
(
<
8
5
显示:(-8) 5
<
-32768.
=
)
(-)
(
<
3
6
显示:(-3) 6
<
所以(-8)5=-32768,(-3)6=729.
例题讲解
要点1 有理数的乘方的意义
求n个相同因数的 的运算,叫做乘方.乘方的结果叫做幂.在an中,a叫做 ,n叫做 .当an看作a的运算时,读作“ ”,当an看作a的n次方的结果时,也可读作“ ”.
?
积
底数
指数
a的n次方
a的n次幂
课后练习
要点2 有理数乘方的运算
1. 正数的任何次幂都是 ;负数的奇次幂是 .负数的偶次幂是 ;0的任何正整数次幂都是 .
2. 有理数乘方的性质是确定乘方结果的 ,最终的结果还要结合乘方的意义进行计算.
要点3 利用计算器计算有理数的乘方
用计算器计算时,要弄清计算器的每个按键的作用,结合有理数运算的顺序,进行计算.
正数
负数
正数
0
符号
课后练习
1. 下列各组数中:
①-52与(-5)2;②(-3)3与-33;③-(-0.3)5与0.35;④0100与0200;⑤(-1)3与(-1)2,相等的共有( )
A. 1组 B. 2组 C. 3组 D. 4组
C
课后练习
2.计算:
解:
课后练习
3.当n是正整数时,(-1)2n+1-(-1)2n的值是( )
A.2 B.-2 C.0 D.2或-2
B
课后练习
4.a是任意有理数,下列说法正确的是( )
A.(a+1)2的值总是正数
B.a2+1的值总是正数
C.-(a+1)2的值总是负数
D.a2+1的值中最大的是1
B
课后练习
解:
课后练习
6.规定“☆”是一种运算符号,且a☆b=ab-ba,
例如:2☆3=23-32=8-9=-1,
试计算4☆(3☆2)的值.
4☆(3☆2)=4☆(32-23)
=4☆1
=41-14
=3
解:
所以4☆(3☆2)的值是3.
课后练习
7. 小明在电脑上设计了一个有理数运算的程序:输入a,#键,再输入b,得到运算a#b=a2-b2-2ab,求(-2)#3的值.
解:(-2)#3=(-2)2-32-2×(-2)×3=7.
课后练习
1.求几个相同因数的积的运算,叫做乘方.
2.乘方的符号法则:
(1)正数的任何次幂都是正数
(2)负数的奇次幂是负数,负数的偶次幂是正数
(3)零的正整数次幂都是零
幂
指数
底数
课堂总结
教材练习题1—3题.
课后作业
谢
谢
观
看
