人教版八年级数学上册同步练习:12.3第1课时角的平分线的性质(word版,含答案)
文档属性
| 名称 | 人教版八年级数学上册同步练习:12.3第1课时角的平分线的性质(word版,含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 188.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-21 18:02:38 | ||
图片预览


文档简介
12.3 第1课时 角的平分线的性质
一、选择题
1.如图1,利用尺规作∠AOB的平分线OC,其作法如下:(1)以点O为圆心,适当长为半径画弧,与OA,OB分别交于点D,E;
(2)分别以点D,E为圆心,大于DE的长为半径画弧,两弧在∠AOB的内部交于点C;
(3)画射线OC,则射线OC就是∠AOB的平分线.
这样作图的原理是三角形全等的一种判定方法,这种判定方法是
( )
图1
A.SSS
B.SAS
C.ASA
D.AAS
2.如图2,点A在点O的北偏西30°的方向上,AB⊥OA,垂足为A.根据已知条件和图上尺规作图的痕迹判断,下列说法正确的是
( )
A.点O在点A的南偏东60°方向上
B.点B在点A的北偏东30°方向上
C.点B在点O的北偏东60°方向上
D.点B在点O的北偏东30°方向上
图2
3.如图3,AB∥CD,以点A为圆心,小于AC的长为半径画弧,与AB,AC分别交于点E,F,再分别以点E,F为圆心,大于EF的长为半径画弧,两弧在∠CAB的内部交于点G,作射线AG交CD于点H.若∠C=140°,则∠AHC的大小是
( )
图3
A.20°
B.25°
C.30°
D.40°
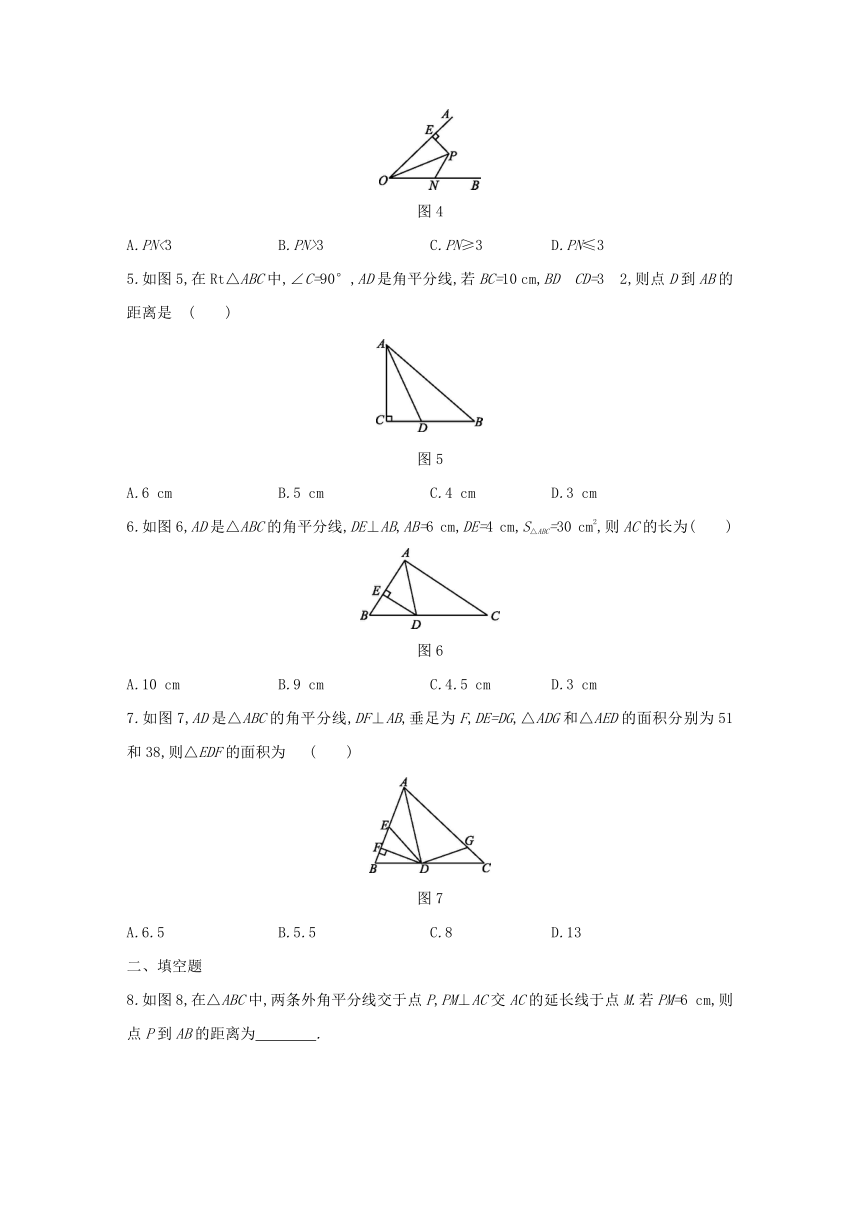
4.如图4,OP平分∠AOB,点P到OA的距离为3,N是OB上的任意一点,则线段PN的长度的取值范围为
( )
图4
A.PN<3
B.PN>3
C.PN≥3
D.PN≤3
5.如图5,在Rt△ABC中,∠C=90°,AD是角平分线,若BC=10
cm,BD?CD=3?2,则点D到AB的距离是
( )
图5
A.6
cm
B.5
cm
C.4
cm
D.3
cm
6.如图6,AD是△ABC的角平分线,DE⊥AB,AB=6
cm,DE=4
cm,S△ABC=30
cm2,则AC的长为( )
图6
A.10
cm
B.9
cm
C.4.5
cm
D.3
cm
7.如图7,AD是△ABC的角平分线,DF⊥AB,垂足为F,DE=DG,△ADG和△AED的面积分别为51和38,则△EDF的面积为
( )
图7
A.6.5
B.5.5
C.8
D.13
二、填空题
8.如图8,在△ABC中,两条外角平分线交于点P,PM⊥AC交AC的延长线于点M.若PM=6
cm,则点P到AB的距离为 .?
图8
9.如图9,在△ABC中,E为AC的中点,AD平分∠BAC交BC于点D,AB︰AC=2︰3,AD与BE相交于点O.若△OAE的面积比△BOD的面积大1,则△ABC的面积是 .?
图9
三、解答题
10.如图10,已知点B,D分别在∠MAN的两边上,C为∠MAN内部的一点,且AB=AD,DC=BC,CE⊥AM于点E,CF⊥AN于点F.试判断CE与CF是否相等,并说明理由.
图10
11.如图11,已知∠1=∠2,BA图11
12.证明命题“角的平分线上的点到角的两边的距离相等”,要根据题意,画出图形,并用符号表示已知和求证,写出证明过程.下面是小明同学根据题意画出的图形,并写出了不完整的已知和求证.
已知:如图12,∠AOC=∠BOC,点P在OC上,
.?
求证: .?
请你补全已知和求证,并写出证明过程.
图12
13.如图13,已知AD∥BC,∠D=90°.
(1)如图①,若∠DAB的平分线与∠CBA的平分线交于点P,CD经过点P,则P是线段CD的中点吗?为什么?
(2)如图②,若P是DC的中点,BP平分∠ABC,∠CPB=35°,求∠PAD的度数.
图13
答案
1.A
2.D
3.A .
4.C
5.C
6.B
7.A
8.6
cm
9.10 [
10.解:CE=CF.
理由:在△ACD和△ACB中,
∴△ACD≌△ACB.
∴∠DAC=∠BAC,
即AC平分∠MAN.
又∵CE⊥AM,CF⊥AN,
∴CE=CF(角的平分线上的点到角的两边的距离相等).
11.证明:如图,过点P作PE⊥BA交BA的延长线于点E.又∵∠1=∠2,PF⊥BC,
∴PE=PF,∠PEA=∠PFC=90°.
在Rt△PEA与Rt△PFC中,
∴Rt△PEA≌Rt△PFC(HL).
∴∠PAE=∠PCB.
∵∠PAE+∠BAP=180°,
∴∠PCB+∠BAP=180°.
12.解:PD⊥OA,PE⊥OB,垂足分别为D,E
PD=PE
证明:∵PD⊥OA,PE⊥OB,
∴∠PDO=∠PEO=90°.
在△PDO和△PEO中,
∴△PDO≌△PEO(AAS).∴PD=PE.
13.解:(1)P是线段CD的中点.
理由如下:过点P作PE⊥AB于点E.
∵AD∥BC,∠D=90°,∴∠C=180°-∠D=90°,即PC⊥BC.∵∠DAB的平分线与∠CBA的平分线交于点P,∴PD=PE,PC=PE.∴PC=PD,即P是线段CD的中点.
(2)过点P作PE⊥AB于点E.
∵AD∥BC,∠D=90°,
∴∠C=180°-∠D=90°,即PC⊥BC.
∵BP平分∠ABC,
∴∠PBE=∠PBC.
在△PBE与△PBC中,
∴△PBE≌△PBC(AAS).
∴∠EPB=∠CPB=35°,PE=PC.
∵PC=PD,∴PD=PE.
在Rt△PAD与Rt△PAE中,
∴Rt△PAD≌Rt△PAE(HL).
∴∠APD=∠APE.
∵∠APD+∠APE=180°-2×35°=110°,
∴∠APD=55°.
∴∠PAD=90°-∠APD=35°.
一、选择题
1.如图1,利用尺规作∠AOB的平分线OC,其作法如下:(1)以点O为圆心,适当长为半径画弧,与OA,OB分别交于点D,E;
(2)分别以点D,E为圆心,大于DE的长为半径画弧,两弧在∠AOB的内部交于点C;
(3)画射线OC,则射线OC就是∠AOB的平分线.
这样作图的原理是三角形全等的一种判定方法,这种判定方法是
( )
图1
A.SSS
B.SAS
C.ASA
D.AAS
2.如图2,点A在点O的北偏西30°的方向上,AB⊥OA,垂足为A.根据已知条件和图上尺规作图的痕迹判断,下列说法正确的是
( )
A.点O在点A的南偏东60°方向上
B.点B在点A的北偏东30°方向上
C.点B在点O的北偏东60°方向上
D.点B在点O的北偏东30°方向上
图2
3.如图3,AB∥CD,以点A为圆心,小于AC的长为半径画弧,与AB,AC分别交于点E,F,再分别以点E,F为圆心,大于EF的长为半径画弧,两弧在∠CAB的内部交于点G,作射线AG交CD于点H.若∠C=140°,则∠AHC的大小是
( )
图3
A.20°
B.25°
C.30°
D.40°
4.如图4,OP平分∠AOB,点P到OA的距离为3,N是OB上的任意一点,则线段PN的长度的取值范围为
( )
图4
A.PN<3
B.PN>3
C.PN≥3
D.PN≤3
5.如图5,在Rt△ABC中,∠C=90°,AD是角平分线,若BC=10
cm,BD?CD=3?2,则点D到AB的距离是
( )
图5
A.6
cm
B.5
cm
C.4
cm
D.3
cm
6.如图6,AD是△ABC的角平分线,DE⊥AB,AB=6
cm,DE=4
cm,S△ABC=30
cm2,则AC的长为( )
图6
A.10
cm
B.9
cm
C.4.5
cm
D.3
cm
7.如图7,AD是△ABC的角平分线,DF⊥AB,垂足为F,DE=DG,△ADG和△AED的面积分别为51和38,则△EDF的面积为
( )
图7
A.6.5
B.5.5
C.8
D.13
二、填空题
8.如图8,在△ABC中,两条外角平分线交于点P,PM⊥AC交AC的延长线于点M.若PM=6
cm,则点P到AB的距离为 .?
图8
9.如图9,在△ABC中,E为AC的中点,AD平分∠BAC交BC于点D,AB︰AC=2︰3,AD与BE相交于点O.若△OAE的面积比△BOD的面积大1,则△ABC的面积是 .?
图9
三、解答题
10.如图10,已知点B,D分别在∠MAN的两边上,C为∠MAN内部的一点,且AB=AD,DC=BC,CE⊥AM于点E,CF⊥AN于点F.试判断CE与CF是否相等,并说明理由.
图10
11.如图11,已知∠1=∠2,BA
12.证明命题“角的平分线上的点到角的两边的距离相等”,要根据题意,画出图形,并用符号表示已知和求证,写出证明过程.下面是小明同学根据题意画出的图形,并写出了不完整的已知和求证.
已知:如图12,∠AOC=∠BOC,点P在OC上,
.?
求证: .?
请你补全已知和求证,并写出证明过程.
图12
13.如图13,已知AD∥BC,∠D=90°.
(1)如图①,若∠DAB的平分线与∠CBA的平分线交于点P,CD经过点P,则P是线段CD的中点吗?为什么?
(2)如图②,若P是DC的中点,BP平分∠ABC,∠CPB=35°,求∠PAD的度数.
图13
答案
1.A
2.D
3.A .
4.C
5.C
6.B
7.A
8.6
cm
9.10 [
10.解:CE=CF.
理由:在△ACD和△ACB中,
∴△ACD≌△ACB.
∴∠DAC=∠BAC,
即AC平分∠MAN.
又∵CE⊥AM,CF⊥AN,
∴CE=CF(角的平分线上的点到角的两边的距离相等).
11.证明:如图,过点P作PE⊥BA交BA的延长线于点E.又∵∠1=∠2,PF⊥BC,
∴PE=PF,∠PEA=∠PFC=90°.
在Rt△PEA与Rt△PFC中,
∴Rt△PEA≌Rt△PFC(HL).
∴∠PAE=∠PCB.
∵∠PAE+∠BAP=180°,
∴∠PCB+∠BAP=180°.
12.解:PD⊥OA,PE⊥OB,垂足分别为D,E
PD=PE
证明:∵PD⊥OA,PE⊥OB,
∴∠PDO=∠PEO=90°.
在△PDO和△PEO中,
∴△PDO≌△PEO(AAS).∴PD=PE.
13.解:(1)P是线段CD的中点.
理由如下:过点P作PE⊥AB于点E.
∵AD∥BC,∠D=90°,∴∠C=180°-∠D=90°,即PC⊥BC.∵∠DAB的平分线与∠CBA的平分线交于点P,∴PD=PE,PC=PE.∴PC=PD,即P是线段CD的中点.
(2)过点P作PE⊥AB于点E.
∵AD∥BC,∠D=90°,
∴∠C=180°-∠D=90°,即PC⊥BC.
∵BP平分∠ABC,
∴∠PBE=∠PBC.
在△PBE与△PBC中,
∴△PBE≌△PBC(AAS).
∴∠EPB=∠CPB=35°,PE=PC.
∵PC=PD,∴PD=PE.
在Rt△PAD与Rt△PAE中,
∴Rt△PAD≌Rt△PAE(HL).
∴∠APD=∠APE.
∵∠APD+∠APE=180°-2×35°=110°,
∴∠APD=55°.
∴∠PAD=90°-∠APD=35°.
