华师大版数学七上 5.1.3 同位角 、内错角、 同旁内角 课件 (共21张ppt)
文档属性
| 名称 | 华师大版数学七上 5.1.3 同位角 、内错角、 同旁内角 课件 (共21张ppt) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-21 00:00:00 | ||
图片预览

文档简介
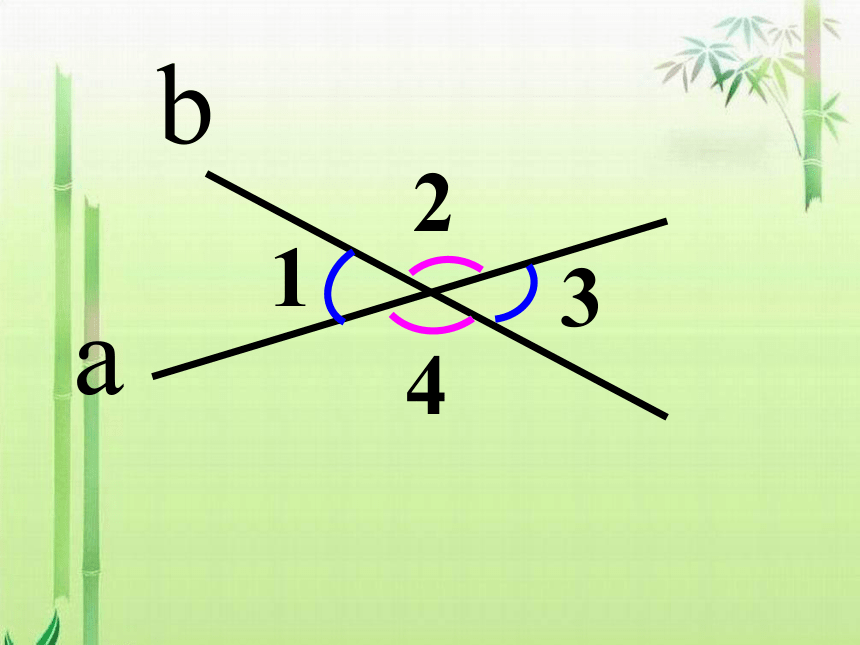
3.同位角 、内错角、 同旁内角
§5.1
2
1
4
3
a
b
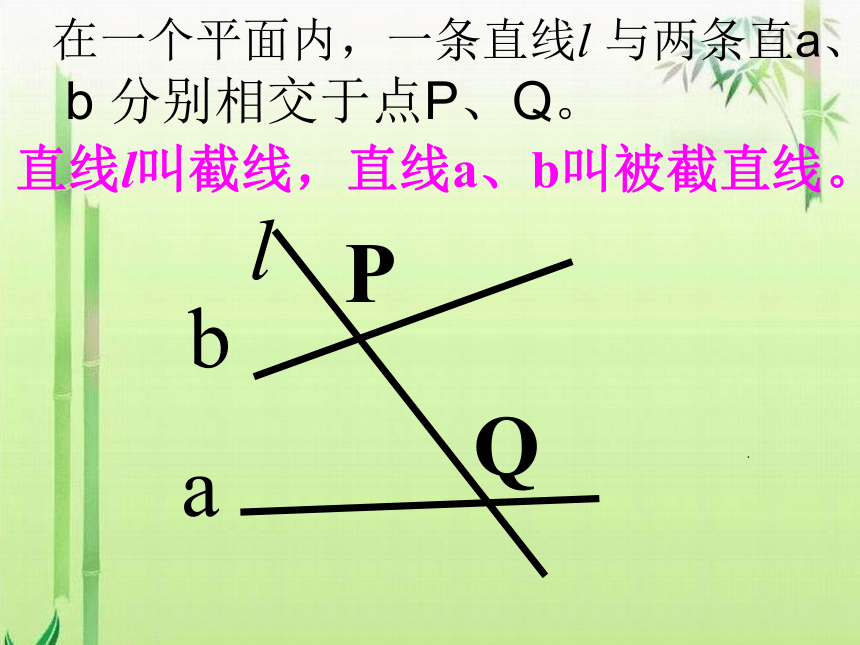
在一个平面内,一条直线l 与两条直a、
b 分别相交于点P、Q。
a
b
P
Q
直线l叫截线,直线a、b叫被截直线。
l
.
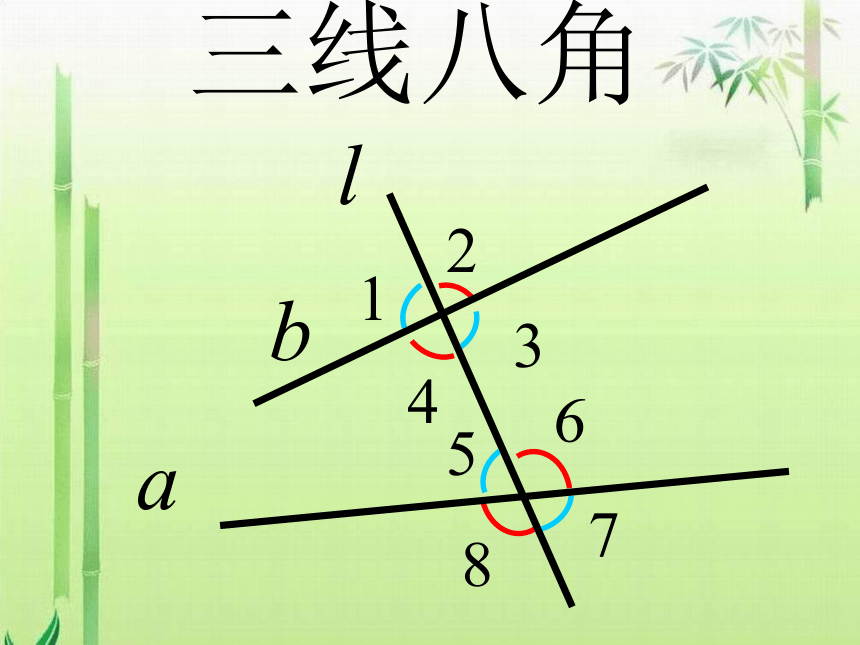
三线八角
a
b
l
5
6
7
8
1
2
3
4
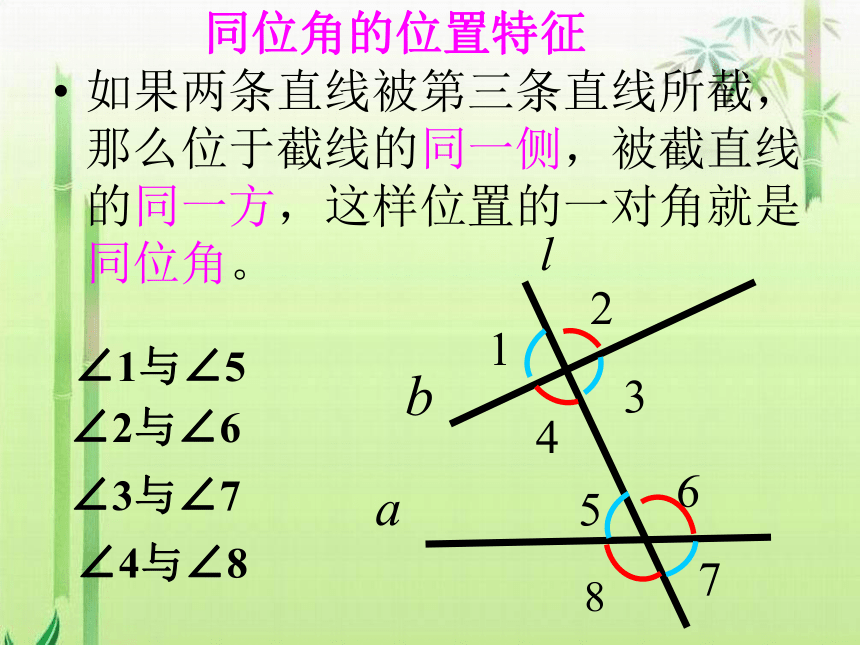
如果两条直线被第三条直线所截,那么位于截线的同一侧,被截直线的同一方,这样位置的一对角就是同位角。
同位角的位置特征
a
b
l
5
6
7
8
1
2
3
4
∠1与∠5
∠4与∠8
∠2与∠6
∠3与∠7
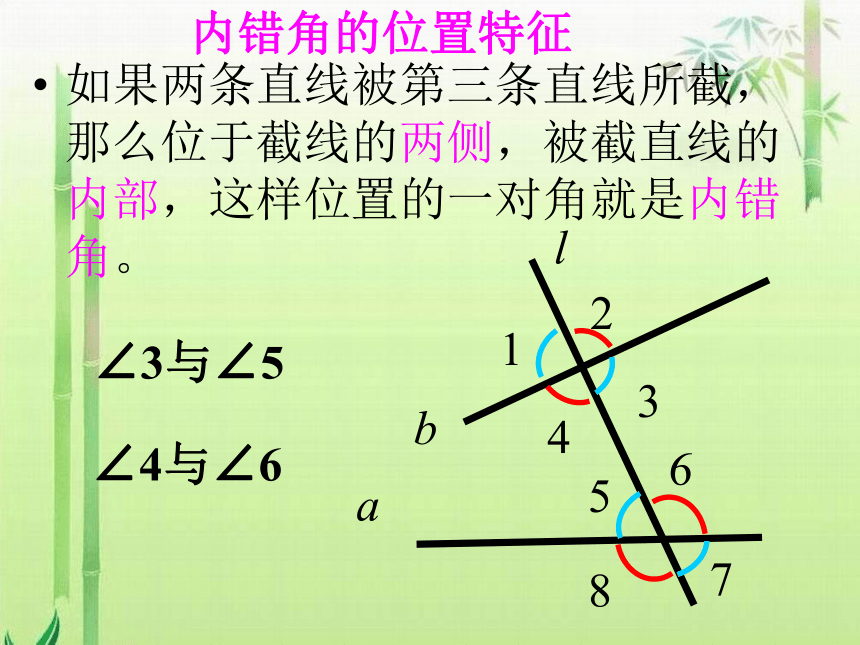
如果两条直线被第三条直线所截,那么位于截线的两侧,被截直线的内部,这样位置的一对角就是内错角。
内错角的位置特征
a
b
l
5
6
7
8
1
2
3
4
∠4与∠6
∠3与∠5
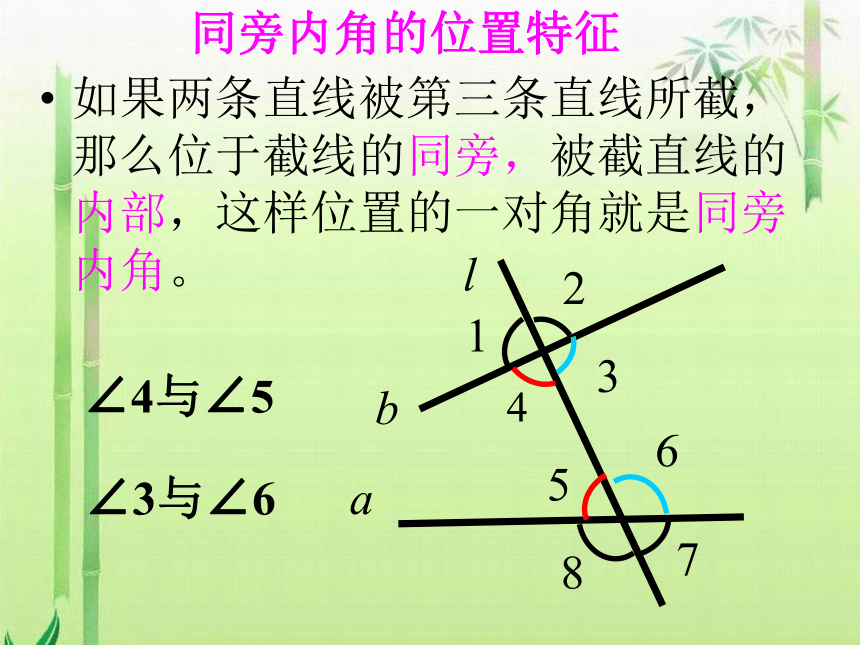
如果两条直线被第三条直线所截,那么位于截线的同旁,被截直线的内部,这样位置的一对角就是同旁内角。
同旁内角的位置特征
a
b
l
5
6
7
8
1
2
3
4
∠4与∠5
∠3与∠6
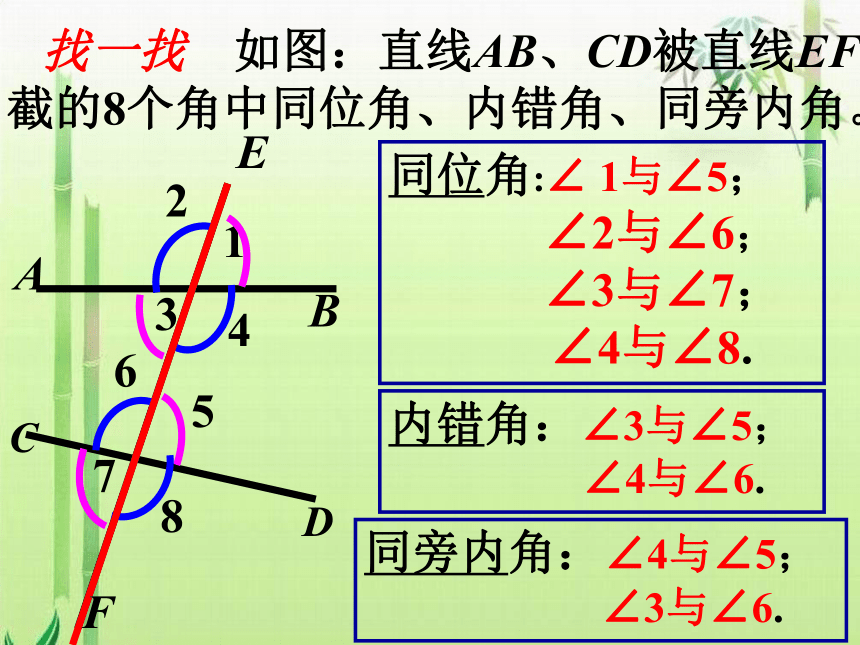
同位角:∠ 1与∠5;
∠2与∠6;
∠3与∠7;
∠4与∠8.
内错角:∠3与∠5;
∠4与∠6.
2
3
4
1
7
8
5
6
C
A
E
B
D
F
同旁内角:∠4与∠5;
∠3与∠6.
找一找 如图:直线AB、CD被直线EF
截的8个角中同位角、内错角、同旁内角。
2
3
4
1
7
8
5
6
C
A
E
B
D
F
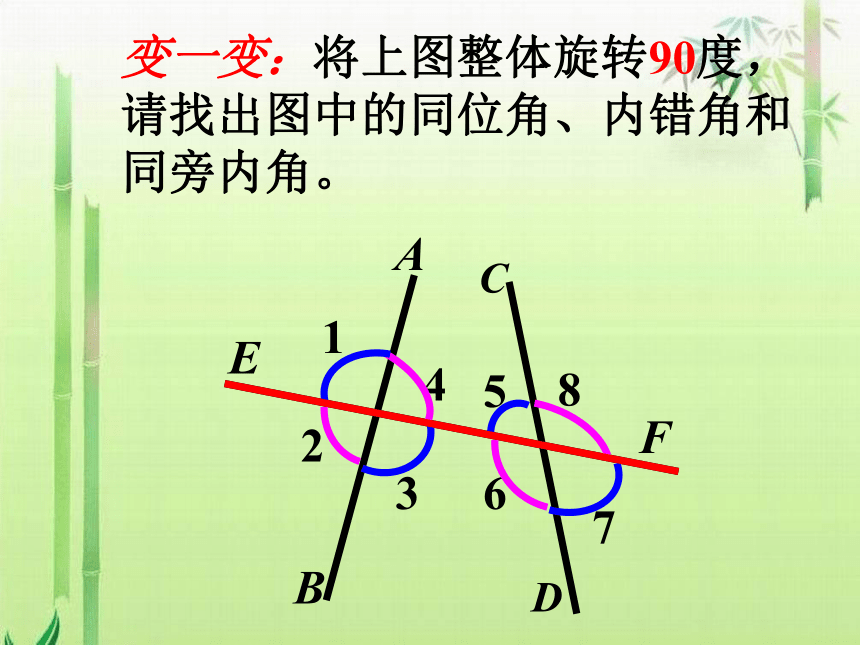
变一变:将上图整体旋转90度,请找出图中的同位角、内错角和同旁内角。
B
A
C
D
E
3
2
1
4
做一做: 1.如图,直线DE,BC被直线AB所截,
∠1与∠2是 角,∠1与∠3是___角,
∠1与∠4是___角。
内错
同旁内
同位
2.
内错
同旁内
同位
如图:∠1与∠2是同位角吗?
辩一辩 :
B
C
C
A
B
A
G
E
(1)
(2)
F
D
如图:∠1与∠2是内错角吗?
(1)
(2)
A
B
C
A
B
C
D
E
如图:∠1与∠2是同旁内角吗?
(1)
A
B
C
(2)
A
B
C
D
E
F
列一列
你会把同位角、内错角、同旁内角的位置特征及图形特征列成表吗?
特征
角
位置特征
图形特征(象英文字母)
在两条被截直线
在截线
同 位 角
内 错 角
同旁内角
同一方
同一侧
“ F ”
内 部
两 侧 ( 交 错)
内 部
同旁
“ Z ”
“ U ”
根据图形按要求填空:
(1)∠1与∠2是直线
和 被直线
所截
而得的 .
A
B
C
D
E
F
1
3
5
2
4
露一手:
BC
AB
DE
同位角
A
B
C
D
E
F
1
3
5
2
4
(3)∠3与∠4是直线 ____和 __被直线
____所截而得的_______.
(2) ∠1与∠3是直
线 和 被直线
所截而得的 .
BC
DE
AB
内错角
BC
EF
DE
内错角
A
B
C
D
E
F
1
3
5
2
4
(4)∠2与∠4是直
线_____和 被直
线 所截而得的 _____ .
(5)∠4与∠5是直
线____和____被直
线____所截而得的
_________.
BC
EF
DE
同位角
DE
EF
同旁内角
BC
课堂小结
主要内容:本节课主要学习了两条直线被 第三条直线所截而产生的三种角——同位角、内错角、同旁内角及其位置特征.
1、三种角产生的条件及位置特征;
注意:
2、判断时应先找到“截线”,再找另外两条
“被截直线”,然后根据角的位置决定是哪一种角.
3、 如果两个角都有一条边在某条直线上,那么这条直线就是“截线”,另两边所在直线就是“被截直线”。
1.P168练习的第1题,2题(必做题,做在书上)。 2.P168习题5.1的第2题,3 题(必做题,做在书上)。
布置作业:
§5.1
2
1
4
3
a
b
在一个平面内,一条直线l 与两条直a、
b 分别相交于点P、Q。
a
b
P
Q
直线l叫截线,直线a、b叫被截直线。
l
.
三线八角
a
b
l
5
6
7
8
1
2
3
4
如果两条直线被第三条直线所截,那么位于截线的同一侧,被截直线的同一方,这样位置的一对角就是同位角。
同位角的位置特征
a
b
l
5
6
7
8
1
2
3
4
∠1与∠5
∠4与∠8
∠2与∠6
∠3与∠7
如果两条直线被第三条直线所截,那么位于截线的两侧,被截直线的内部,这样位置的一对角就是内错角。
内错角的位置特征
a
b
l
5
6
7
8
1
2
3
4
∠4与∠6
∠3与∠5
如果两条直线被第三条直线所截,那么位于截线的同旁,被截直线的内部,这样位置的一对角就是同旁内角。
同旁内角的位置特征
a
b
l
5
6
7
8
1
2
3
4
∠4与∠5
∠3与∠6
同位角:∠ 1与∠5;
∠2与∠6;
∠3与∠7;
∠4与∠8.
内错角:∠3与∠5;
∠4与∠6.
2
3
4
1
7
8
5
6
C
A
E
B
D
F
同旁内角:∠4与∠5;
∠3与∠6.
找一找 如图:直线AB、CD被直线EF
截的8个角中同位角、内错角、同旁内角。
2
3
4
1
7
8
5
6
C
A
E
B
D
F
变一变:将上图整体旋转90度,请找出图中的同位角、内错角和同旁内角。
B
A
C
D
E
3
2
1
4
做一做: 1.如图,直线DE,BC被直线AB所截,
∠1与∠2是 角,∠1与∠3是___角,
∠1与∠4是___角。
内错
同旁内
同位
2.
内错
同旁内
同位
如图:∠1与∠2是同位角吗?
辩一辩 :
B
C
C
A
B
A
G
E
(1)
(2)
F
D
如图:∠1与∠2是内错角吗?
(1)
(2)
A
B
C
A
B
C
D
E
如图:∠1与∠2是同旁内角吗?
(1)
A
B
C
(2)
A
B
C
D
E
F
列一列
你会把同位角、内错角、同旁内角的位置特征及图形特征列成表吗?
特征
角
位置特征
图形特征(象英文字母)
在两条被截直线
在截线
同 位 角
内 错 角
同旁内角
同一方
同一侧
“ F ”
内 部
两 侧 ( 交 错)
内 部
同旁
“ Z ”
“ U ”
根据图形按要求填空:
(1)∠1与∠2是直线
和 被直线
所截
而得的 .
A
B
C
D
E
F
1
3
5
2
4
露一手:
BC
AB
DE
同位角
A
B
C
D
E
F
1
3
5
2
4
(3)∠3与∠4是直线 ____和 __被直线
____所截而得的_______.
(2) ∠1与∠3是直
线 和 被直线
所截而得的 .
BC
DE
AB
内错角
BC
EF
DE
内错角
A
B
C
D
E
F
1
3
5
2
4
(4)∠2与∠4是直
线_____和 被直
线 所截而得的 _____ .
(5)∠4与∠5是直
线____和____被直
线____所截而得的
_________.
BC
EF
DE
同位角
DE
EF
同旁内角
BC
课堂小结
主要内容:本节课主要学习了两条直线被 第三条直线所截而产生的三种角——同位角、内错角、同旁内角及其位置特征.
1、三种角产生的条件及位置特征;
注意:
2、判断时应先找到“截线”,再找另外两条
“被截直线”,然后根据角的位置决定是哪一种角.
3、 如果两个角都有一条边在某条直线上,那么这条直线就是“截线”,另两边所在直线就是“被截直线”。
1.P168练习的第1题,2题(必做题,做在书上)。 2.P168习题5.1的第2题,3 题(必做题,做在书上)。
布置作业:
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
