华师大版数学七上 5.2.2 平行线的判定 课件 (共16张ppt)
文档属性
| 名称 | 华师大版数学七上 5.2.2 平行线的判定 课件 (共16张ppt) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-21 19:45:14 | ||
图片预览



文档简介
七年级 数学
5.2.2 平行线的判定
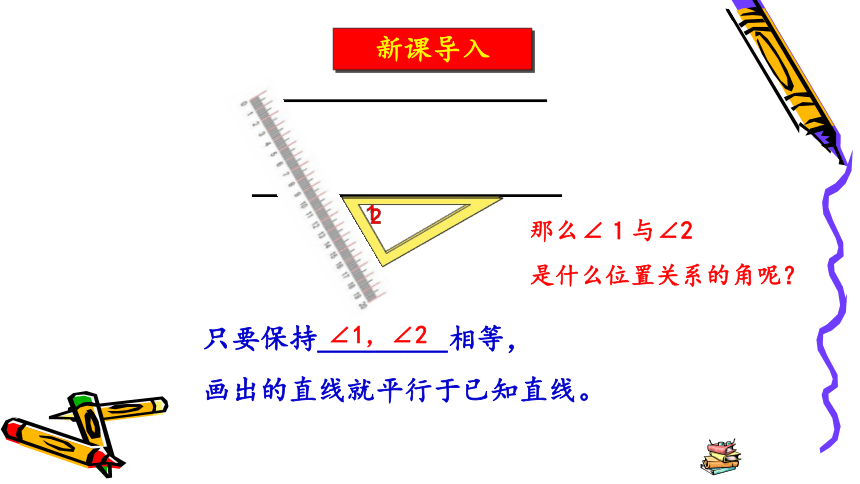
只要保持_________相等,
画出的直线就平行于已知直线。
∠1,∠2
那么∠1与∠2
是什么位置关系的角呢?
新课导入
学习目标:
1.经历“平行线的判定方法”的发现过程。
2.掌握平行线的判定方法。
3.会用它进行简单的推理和表述。
符号语言:∵∠1=∠2(已知)∴a∥b( )
∵∠3=∠2(已知) ∴a∥b( )
∵∠2+∠4= ∴a∥b( )
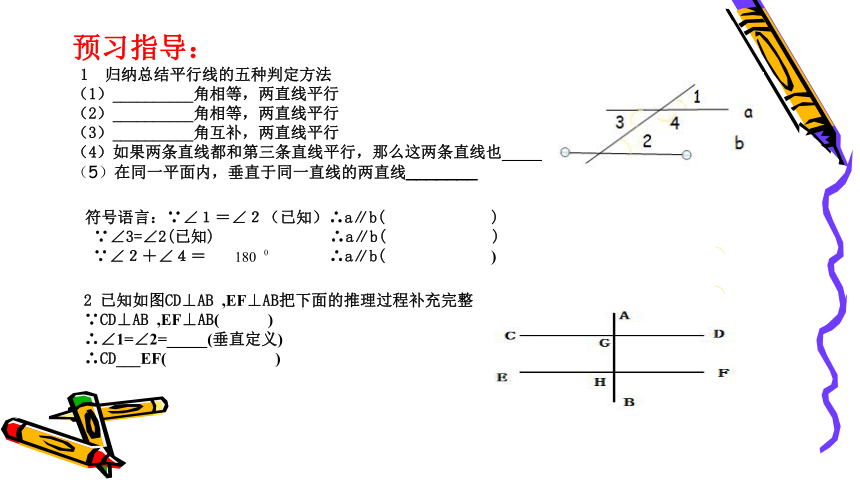
预习指导:
1 归纳总结平行线的五种判定方法
(1)__________角相等,两直线平行
(2)__________角相等,两直线平行
(3)__________角互补,两直线平行
(4)如果两条直线都和第三条直线平行,那么这两条直线也_________
(5)在同一平面内,垂直于同一直线的两直线_______
2 已知如图CD⊥AB ,EF⊥AB把下面的推理过程补充完整
∵CD⊥AB ,EF⊥AB( )
∴∠1=∠2=_____(垂直定义)
∴CD___EF( )
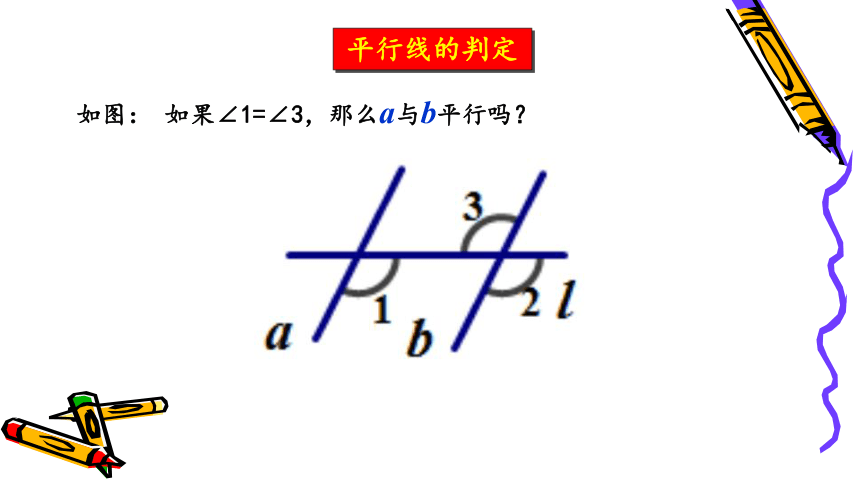
平行线的判定
两条直线被第三条直线所截,如果同位角相等,那么两直线平行。简单地说:
同位角相等,两直线平行。
解:∵ ∠1=∠2(已知)
∴ a∥b(同位角相等,两直线平行)
a
b
l
2
1
如图: 如果∠1=∠3,那么a与b平行吗?
平行线的判定
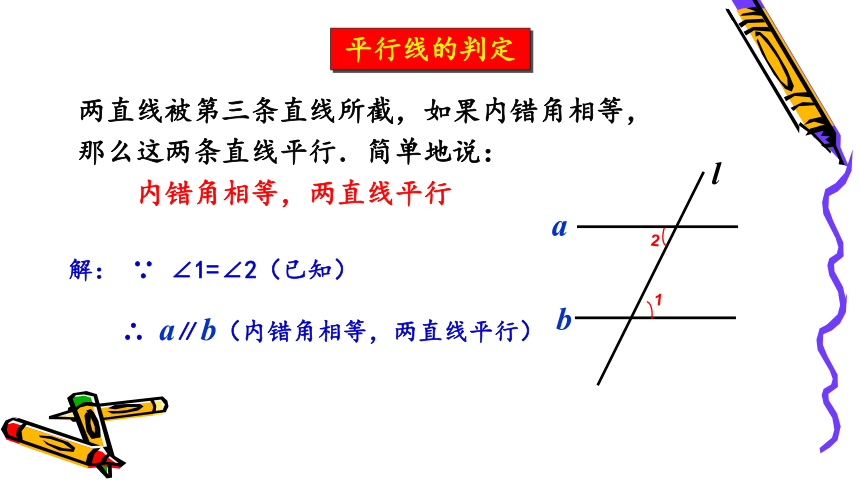
两直线被第三条直线所截,如果内错角相等,
那么这两条直线平行.简单地说:
内错角相等,两直线平行
a
b
l
1
2
解: ∵ ∠1=∠2(已知)
∴ a∥b(内错角相等,两直线平行)
平行线的判定
如图,直线a,b被直线 l 所截,若∠1+∠3=180°
则a∥b吗?为什么?
解:∵ ∠1+∠3= 180°
∠2+∠3= 180°(已知)
∴ ∠1=∠2 (等量代换)
∴ a∥b(同位角相等,两直线平行)
平行线的判定
等量代换是指一个量用与它相等的量去代替
两直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.简单地说:
同旁内角互补,两直线平行
解:∵ ∠1 + ∠2 =180° (已知)
∴a∥b(同旁内角互补,两直线平行)
平行线的判定
如图,直线a,b被直线l所截,已知∠1=115°,
∠2=115°,直线a、b平行吗?为什么?
解:∵ ∠1=115°,∠2=115° (已知)
∴∠1=∠2 (等量代换)
∴a∥b(内错角相等,两直线平行)
自主学习
如图,在四边形ABCD中,已知∠B=60°, ∠C=120°
AB与CD平行吗? AD与BC平行吗?
解:∵ ∠B=60°, ∠C=120° (已知)
∴∠B+∠C=180°(等式的性质)
∴AB∥CD (同旁内角互补,两直线平行)
本题中,根据题目的条件,无法判定AD与BC平行
A
B
C
D
合作探究
等式的性质是指等式的左右两边同时加上(或减去,乘以,除以一个不为0)的数,等式仍相等
平行线的判定法:
1.同位角相等,两直线平行。
2.内错角相等,两直线平行
3.同旁内角互补,两直线平行
课堂小结
当堂检测
1.在下列解答中,填上适当的理由
(1)∵∠B=∠1(已知)
∴AD∥BC( )
(2)∵∠D=∠1(已知)
∴AB∥CD( )
2.在下列解答中,填空:
(1)∵∠BAD+∠ABC=180°(已知)
∴( )∥( )(同旁内角互补,两直线平行)
(2)∵∠BCD+∠ABC=180°(已知)
∴( )∥( )(同旁内角互补,两直线平行)
同位角相等,两直线平行
内错角相等,两直线平行
AD
BC
AB
CD
a
b
c
m
n
1
2
3
4
a ∥ b
c ∥ m
c ∥ n
当图中各角满足下列条件时,请指出哪两条直线平行 , 并说出根据。
(1)∠1=∠4
当堂检测
(2)∠2=∠4
(3)∠1+∠3=180°
同位角相等,两直线平行
内错角相等,两直线平行
同旁内角互补,两直线平行
已知:如图,直线AB、CD被直线EF所截,且∠1=60°, ∠2=120°,那么AB与CD平行吗?为什么?
A
B
D
C
E
F
1
2
3
4
5
解:
∵∠2=120°(已知)
∴∠4=∠2= 120° (对顶角相等)
∵ ∠1=60° (已知)
∴∠1+∠4= 60°+ 120°= 180°(等式的性质)
∴AB∥CD(同旁内角互补,两直线平行)
当堂检测
四清导航87-88页
课后作业
5.2.2 平行线的判定
只要保持_________相等,
画出的直线就平行于已知直线。
∠1,∠2
那么∠1与∠2
是什么位置关系的角呢?
新课导入
学习目标:
1.经历“平行线的判定方法”的发现过程。
2.掌握平行线的判定方法。
3.会用它进行简单的推理和表述。
符号语言:∵∠1=∠2(已知)∴a∥b( )
∵∠3=∠2(已知) ∴a∥b( )
∵∠2+∠4= ∴a∥b( )
预习指导:
1 归纳总结平行线的五种判定方法
(1)__________角相等,两直线平行
(2)__________角相等,两直线平行
(3)__________角互补,两直线平行
(4)如果两条直线都和第三条直线平行,那么这两条直线也_________
(5)在同一平面内,垂直于同一直线的两直线_______
2 已知如图CD⊥AB ,EF⊥AB把下面的推理过程补充完整
∵CD⊥AB ,EF⊥AB( )
∴∠1=∠2=_____(垂直定义)
∴CD___EF( )
平行线的判定
两条直线被第三条直线所截,如果同位角相等,那么两直线平行。简单地说:
同位角相等,两直线平行。
解:∵ ∠1=∠2(已知)
∴ a∥b(同位角相等,两直线平行)
a
b
l
2
1
如图: 如果∠1=∠3,那么a与b平行吗?
平行线的判定
两直线被第三条直线所截,如果内错角相等,
那么这两条直线平行.简单地说:
内错角相等,两直线平行
a
b
l
1
2
解: ∵ ∠1=∠2(已知)
∴ a∥b(内错角相等,两直线平行)
平行线的判定
如图,直线a,b被直线 l 所截,若∠1+∠3=180°
则a∥b吗?为什么?
解:∵ ∠1+∠3= 180°
∠2+∠3= 180°(已知)
∴ ∠1=∠2 (等量代换)
∴ a∥b(同位角相等,两直线平行)
平行线的判定
等量代换是指一个量用与它相等的量去代替
两直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.简单地说:
同旁内角互补,两直线平行
解:∵ ∠1 + ∠2 =180° (已知)
∴a∥b(同旁内角互补,两直线平行)
平行线的判定
如图,直线a,b被直线l所截,已知∠1=115°,
∠2=115°,直线a、b平行吗?为什么?
解:∵ ∠1=115°,∠2=115° (已知)
∴∠1=∠2 (等量代换)
∴a∥b(内错角相等,两直线平行)
自主学习
如图,在四边形ABCD中,已知∠B=60°, ∠C=120°
AB与CD平行吗? AD与BC平行吗?
解:∵ ∠B=60°, ∠C=120° (已知)
∴∠B+∠C=180°(等式的性质)
∴AB∥CD (同旁内角互补,两直线平行)
本题中,根据题目的条件,无法判定AD与BC平行
A
B
C
D
合作探究
等式的性质是指等式的左右两边同时加上(或减去,乘以,除以一个不为0)的数,等式仍相等
平行线的判定法:
1.同位角相等,两直线平行。
2.内错角相等,两直线平行
3.同旁内角互补,两直线平行
课堂小结
当堂检测
1.在下列解答中,填上适当的理由
(1)∵∠B=∠1(已知)
∴AD∥BC( )
(2)∵∠D=∠1(已知)
∴AB∥CD( )
2.在下列解答中,填空:
(1)∵∠BAD+∠ABC=180°(已知)
∴( )∥( )(同旁内角互补,两直线平行)
(2)∵∠BCD+∠ABC=180°(已知)
∴( )∥( )(同旁内角互补,两直线平行)
同位角相等,两直线平行
内错角相等,两直线平行
AD
BC
AB
CD
a
b
c
m
n
1
2
3
4
a ∥ b
c ∥ m
c ∥ n
当图中各角满足下列条件时,请指出哪两条直线平行 , 并说出根据。
(1)∠1=∠4
当堂检测
(2)∠2=∠4
(3)∠1+∠3=180°
同位角相等,两直线平行
内错角相等,两直线平行
同旁内角互补,两直线平行
已知:如图,直线AB、CD被直线EF所截,且∠1=60°, ∠2=120°,那么AB与CD平行吗?为什么?
A
B
D
C
E
F
1
2
3
4
5
解:
∵∠2=120°(已知)
∴∠4=∠2= 120° (对顶角相等)
∵ ∠1=60° (已知)
∴∠1+∠4= 60°+ 120°= 180°(等式的性质)
∴AB∥CD(同旁内角互补,两直线平行)
当堂检测
四清导航87-88页
课后作业
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
