高中物理粤教版选修3-1 3.6洛伦兹力与现代技术 课件2(31张PPT)
文档属性
| 名称 | 高中物理粤教版选修3-1 3.6洛伦兹力与现代技术 课件2(31张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 30.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 粤教版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-08-22 06:25:15 | ||
图片预览






文档简介
(共31张PPT)
第三章
磁
场
第
六
节
洛伦兹力与现代技术
一、带电粒子在匀强磁场中的运动
(1)带电粒子平行于磁场方向射入时,带电粒子不受力,做__________运动;
(2)带电粒子垂直于磁场方向射入时,洛伦兹力总始终与速度方向______,
所以洛伦兹力对带电粒子______
。
(3)带电粒子垂直于磁场方向射入时,洛伦兹力总与速度方向______,起到向心力的作用,所以带电粒子在匀强磁场中做__________运动.
匀速直线
垂直
匀速圆周
垂直
不做功
课前预习
(4)圆周运动的半径和周期
质量为m、带电量为q的粒子,以速度v垂直射入磁感应强度为B的匀强磁场,粒子做匀速圆周运动所需向心力是由__________提供,根据牛顿第二定律和圆周运动公式求得半径与周期.
洛伦兹力
课前预习
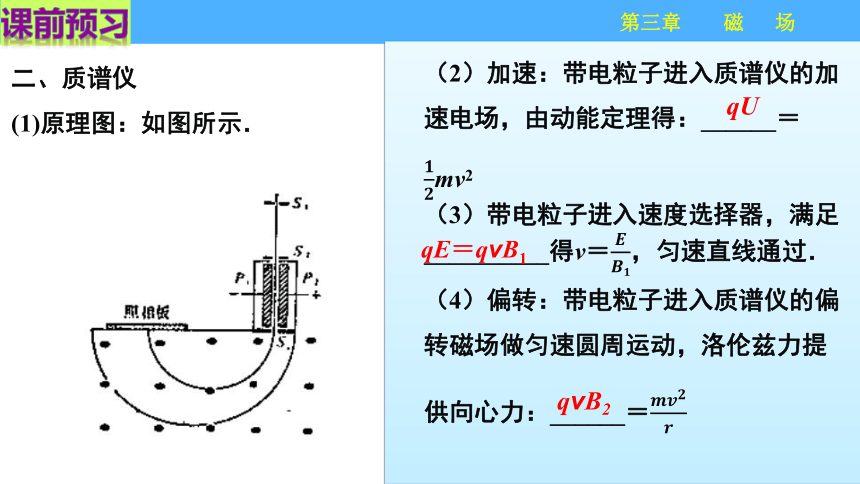
二、质谱仪
(1)原理图:如图所示.
(2)加速:带电粒子进入质谱仪的加速电场,由动能定理得:______=mv2
(3)带电粒子进入速度选择器,满足__________得v=,匀速直线通过.
(4)偏转:带电粒子进入质谱仪的偏转磁场做匀速圆周运动,洛伦兹力提供向心力:______=
qU
qvB2
课前预习
qE=qvB1
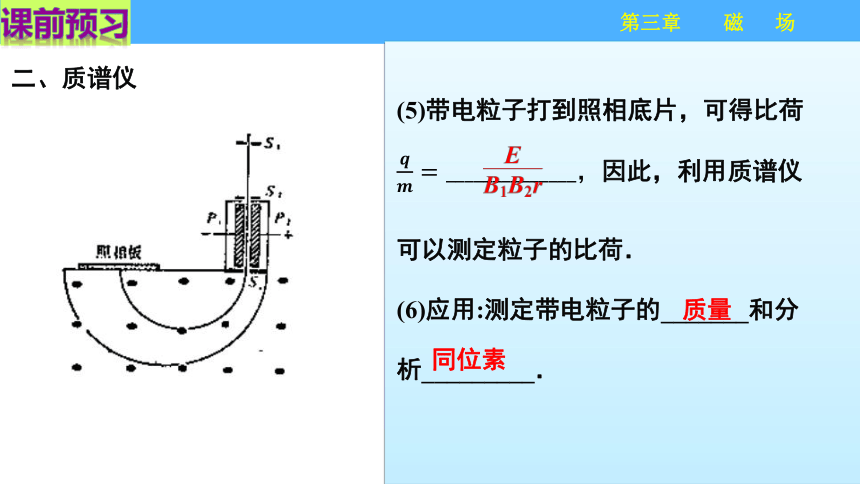
二、质谱仪
(5)带电粒子打到照相底片,可得比荷因此,利用质谱仪可以测定粒子的比荷.
(6)应用:测定带电粒子的_______和分析_________.
质量
同位素
课前预习
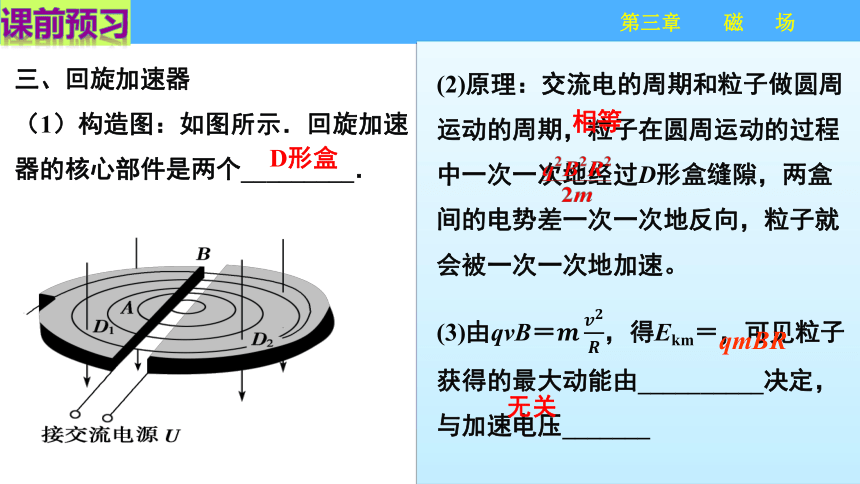
三、回旋加速器
(1)构造图:如图所示.回旋加速器的核心部件是两个_________.
D形盒
(2)原理:交流电的周期和粒子做圆周运动的周期,粒子在圆周运动的过程中一次一次地经过D形盒缝隙,两盒间的电势差一次一次地反向,粒子就会被一次一次地加速。
(3)由qvB=,得Ekm=,可见粒子获得的最大动能由__________决定,与加速电压_______
相等
无关
qmBR
课前预习
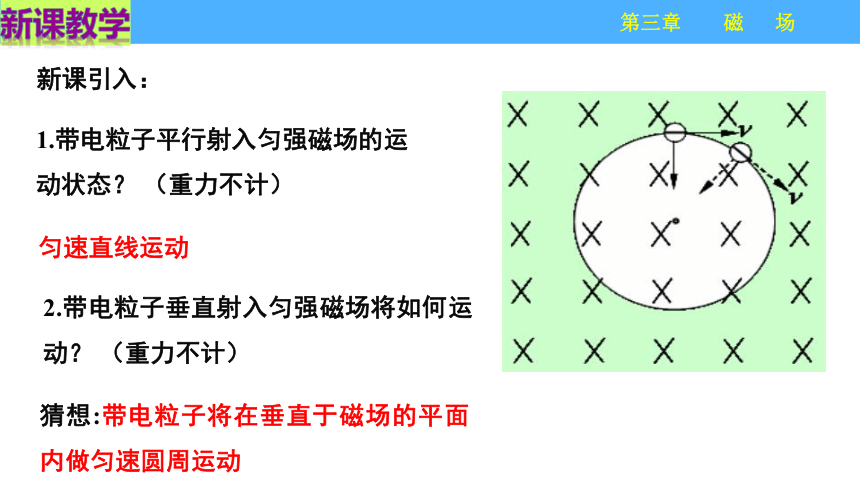
新课引入:
1.带电粒子平行射入匀强磁场的运动状态?
(重力不计)
新课教学
匀速直线运动
2.带电粒子垂直射入匀强磁场将如何运动?
(重力不计)
猜想:带电粒子将在垂直于磁场的平面内做匀速圆周运动
亥姆霍兹线圈
加速电压选择挡
磁场强弱选择挡
电
子
枪
洛伦兹力演示仪
实验验证
新课教学
带电粒子在匀强磁场中的运动
新课教学
实验结论:
1.带电粒子在匀强磁场中做匀速圆周运动
2.粒子做圆周运动的半径与粒子速度有关,半径随速度的增大而增大
3.粒子做圆周运动的半径与磁场强弱有关,半径随磁场的增强而减小
新课教学
1.粒子做圆周运动的半径:
2.粒子做圆周运动的周期
周期T与运动速度及运动半径无关
新课教学
一、带电粒子在磁场中的圆周运动
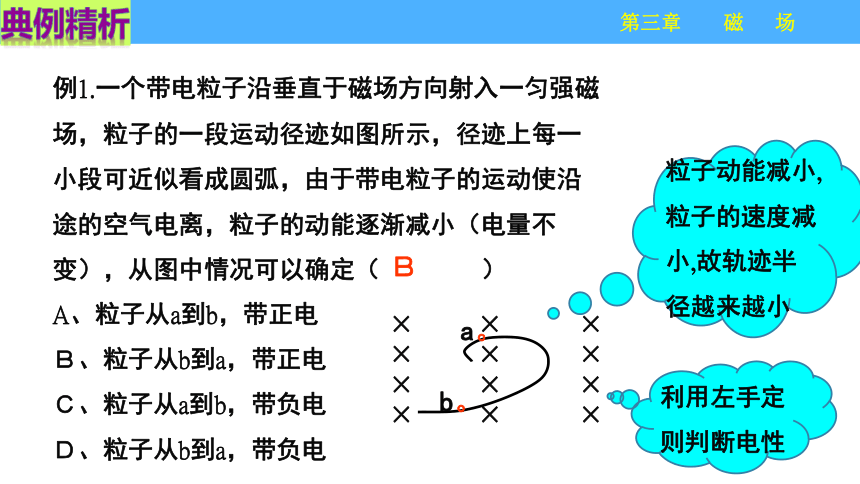
例1.一个带电粒子沿垂直于磁场方向射入一匀强磁场,粒子的一段运动径迹如图所示,径迹上每一小段可近似看成圆弧,由于带电粒子的运动使沿途的空气电离,粒子的动能逐渐减小(电量不变),从图中情况可以确定( )
A、粒子从a到b,带正电
B、粒子从b到a,带正电
C、粒子从a到b,带负电
D、粒子从b到a,带负电
B
典例精析
×
×
×
×
×
×
×
×
×
×
×
×
a。
b。
粒子动能减小,粒子的速度减小,故轨迹半径越来越小
利用左手定则判断电性
二、质谱仪原理分析
1、质谱仪是测量带电粒子质量和分析同位素的重要工具
质谱仪与现代科技
新课教学
2、质谱仪基本原理
新课教学
例2.一个质量为m、电荷量为q的粒子,从容器下方的小孔S1飘入电势差为U的加速电场,然后经过S3沿着与磁场垂直的方向进入磁感应强度为B的匀强磁场中,最后打到照相底片D上求:
(1)求粒子进入磁场时的速率
(2)求粒子在磁场中运动的轨道半径
典例精析
例2.一个质量为m、电荷量为q的粒子,从容器下方的小孔S1飘入电势差为U的加速电场,然后经过S3沿着与磁场垂直的方向进入磁感应强度为B的匀强磁场中,最后打到照相底片D上求:
(1)求粒子进入磁场时的速率
粒子初速度为零
粒子经电场加速
典例精析
例2.一个质量为m、电荷量为q的粒子,从容器下方的小孔S1飘入电势差为U的加速电场,然后经过S3沿着与磁场垂直的方向进入磁感应强度为B的匀强磁场中,最后打到照相底片D上求:
(2)求粒子在磁场中运动的轨道半径
粒子在磁场中做圆周运动,洛伦兹力提供向心力
典例精析
三、回旋加速器
1、直线加速器
原理:利用加速电场对带电粒子做正功使带电粒子的动能增加Ek=qU
由动能定理得带电粒子经几级的电场加速后增加的动能为Ek=q(
U1+U2+U3+··········+Un
)
新课教学
若需要很大的动能的粒子,利用直线加速器是否方便?为什么?那应该怎么办?
2、回旋加速器
(1)构造
新课教学
3、带电粒子的最终能量
当带电粒子的速度最大时,其在磁场中的转动半径也最大,由r=mv/qB知道v=qBr/m
若D形盒的半径为R时,带电粒子的出射速度变为v=qBR/m
所以,带电粒子的最终动能为
即粒子的最终动能由磁感应强度B和D形盒的半径R决定
新课教学
4、交流电的周期:
交流电的周期与粒子在磁场中做圆周运动周期
例3.
回旋加速器盒内的狭缝中有匀强电场,使粒子每次穿过狭缝时都得到加速,两盒放在磁感应强度为B的匀强磁场中,磁场方向垂直于盒底面,粒子源射出的粒子电荷量为q,质量为m,粒子最大回旋半径为R.
(1)粒子在盒内做何种运动;
(2)所加交变电流频率及粒子角速度;
(3)粒子离开加速器时的最大速度及最大动能.
典例精析
例3.
题目已知粒子电荷量为q,质量为m,粒子最大回旋半径为R.
(1)粒子在盒内做何种运动;
答案:带电粒子在盒内在洛伦兹力作用下做匀速圆周运动,每次加速之后半径变大.
典例精析
例3.题目已知粒子电荷量为q,质量为m,粒子最大回旋半径为R.
(2)所加交变电流频率及粒子角速度
提示:交流电的周期等于粒子做圆周运动的周期
解析:(2)
高频交变电流频率要等于粒子回旋频率,因为T=,回旋频率f==,角速度ω=2πf=.
典例精析
例3.题目已知粒子电荷量为q,质量为m,粒子最大回旋半径为R.
(3)粒子离开加速器时的最大速度及最大动能
提示:粒子运动半径等于D形盒时,速度最大,动能最大
解析:(3)由牛顿第二定律知=qBvmax
则Rmax=,vmax=
最大动能Ekmax=m=
典例精析
例4.已知氢核与氦核的质量之比m1∶m2=1∶4,电荷量之比q1∶q2=1∶2,当氢核与氦核以v1∶v2=4∶1的速度,垂直于磁场方向射入磁场后,分别做匀速圆周运动,则氢核与氦核半径之比r1∶r2=________,周期之比T1∶T2=________.
典例精析
由洛伦兹力提供向心力确定半径大小
利用周期公式分析求解
例4.已知:
质量之比m1∶m2=1∶4,
电荷量之比q1∶q2=1∶2,
速度之比v1∶v2=4∶1
求:
半径之比r1∶r2
周期之比T1∶T2
典例精析
答案 2∶1 1∶2
1.两个粒子,电荷量相等,在同一匀强磁场中只受磁场力而做匀速圆周运动( )
A.若速率相等,则半径必相等
B.若质量相等,则周期必相等
C.若周期相等,则半径必相等
D.若动能相等,则半径必相等
答案:B
课堂练习
2.在回旋加速器中( )
A.电场用来加速带电粒子,磁场则使带电粒子回旋
B.电场和磁场同时用来加速带电粒子
C.磁场相同的条件下,回旋加速器的半径越大,则带电粒子获得的动能越大
D.同一带电粒子获得的最大动能只与交流电压的大小有关,而与交流电压的频率无关
答案 AC
课堂练习
3.如图所示,有界匀强磁场边界线SP∥MN,速率不同的同种带电粒子从S点沿SP方向同时射入磁场.其中穿过a点的粒子速度v1与MN垂直;穿过b点的粒子速度v2与MN成60°角,设粒子从S到a、b所需时间分别为t1和t2,则t1∶t2为(重力不计)
( )
A.1∶3
B.4∶3
C.1∶1
D.3∶2
答案 D
课堂练习
4、如图所示,在第Ⅰ象限内有垂直于纸面向里的匀强磁场,一对正、负电子分别以相同速率以与x轴成30°的方向从原点射入磁场,则正、负电子在磁场中运动的时间之比为( )
A.1∶2 B.2∶1
C.1∶
D.1∶1
课堂练习
解析:由T=
可知,正、负电子
的运动周期相同
作出正、负电子运动轨迹如图所示,
正电子运动的圆心角等于120°
负电子运动的圆心角等于60°
由t=,得t正∶t负=θ正∶θ负=2∶1
故B正确.
答案:B
课堂练习
第三章
磁
场
第
六
节
洛伦兹力与现代技术
一、带电粒子在匀强磁场中的运动
(1)带电粒子平行于磁场方向射入时,带电粒子不受力,做__________运动;
(2)带电粒子垂直于磁场方向射入时,洛伦兹力总始终与速度方向______,
所以洛伦兹力对带电粒子______
。
(3)带电粒子垂直于磁场方向射入时,洛伦兹力总与速度方向______,起到向心力的作用,所以带电粒子在匀强磁场中做__________运动.
匀速直线
垂直
匀速圆周
垂直
不做功
课前预习
(4)圆周运动的半径和周期
质量为m、带电量为q的粒子,以速度v垂直射入磁感应强度为B的匀强磁场,粒子做匀速圆周运动所需向心力是由__________提供,根据牛顿第二定律和圆周运动公式求得半径与周期.
洛伦兹力
课前预习
二、质谱仪
(1)原理图:如图所示.
(2)加速:带电粒子进入质谱仪的加速电场,由动能定理得:______=mv2
(3)带电粒子进入速度选择器,满足__________得v=,匀速直线通过.
(4)偏转:带电粒子进入质谱仪的偏转磁场做匀速圆周运动,洛伦兹力提供向心力:______=
qU
qvB2
课前预习
qE=qvB1
二、质谱仪
(5)带电粒子打到照相底片,可得比荷因此,利用质谱仪可以测定粒子的比荷.
(6)应用:测定带电粒子的_______和分析_________.
质量
同位素
课前预习
三、回旋加速器
(1)构造图:如图所示.回旋加速器的核心部件是两个_________.
D形盒
(2)原理:交流电的周期和粒子做圆周运动的周期,粒子在圆周运动的过程中一次一次地经过D形盒缝隙,两盒间的电势差一次一次地反向,粒子就会被一次一次地加速。
(3)由qvB=,得Ekm=,可见粒子获得的最大动能由__________决定,与加速电压_______
相等
无关
qmBR
课前预习
新课引入:
1.带电粒子平行射入匀强磁场的运动状态?
(重力不计)
新课教学
匀速直线运动
2.带电粒子垂直射入匀强磁场将如何运动?
(重力不计)
猜想:带电粒子将在垂直于磁场的平面内做匀速圆周运动
亥姆霍兹线圈
加速电压选择挡
磁场强弱选择挡
电
子
枪
洛伦兹力演示仪
实验验证
新课教学
带电粒子在匀强磁场中的运动
新课教学
实验结论:
1.带电粒子在匀强磁场中做匀速圆周运动
2.粒子做圆周运动的半径与粒子速度有关,半径随速度的增大而增大
3.粒子做圆周运动的半径与磁场强弱有关,半径随磁场的增强而减小
新课教学
1.粒子做圆周运动的半径:
2.粒子做圆周运动的周期
周期T与运动速度及运动半径无关
新课教学
一、带电粒子在磁场中的圆周运动
例1.一个带电粒子沿垂直于磁场方向射入一匀强磁场,粒子的一段运动径迹如图所示,径迹上每一小段可近似看成圆弧,由于带电粒子的运动使沿途的空气电离,粒子的动能逐渐减小(电量不变),从图中情况可以确定( )
A、粒子从a到b,带正电
B、粒子从b到a,带正电
C、粒子从a到b,带负电
D、粒子从b到a,带负电
B
典例精析
×
×
×
×
×
×
×
×
×
×
×
×
a。
b。
粒子动能减小,粒子的速度减小,故轨迹半径越来越小
利用左手定则判断电性
二、质谱仪原理分析
1、质谱仪是测量带电粒子质量和分析同位素的重要工具
质谱仪与现代科技
新课教学
2、质谱仪基本原理
新课教学
例2.一个质量为m、电荷量为q的粒子,从容器下方的小孔S1飘入电势差为U的加速电场,然后经过S3沿着与磁场垂直的方向进入磁感应强度为B的匀强磁场中,最后打到照相底片D上求:
(1)求粒子进入磁场时的速率
(2)求粒子在磁场中运动的轨道半径
典例精析
例2.一个质量为m、电荷量为q的粒子,从容器下方的小孔S1飘入电势差为U的加速电场,然后经过S3沿着与磁场垂直的方向进入磁感应强度为B的匀强磁场中,最后打到照相底片D上求:
(1)求粒子进入磁场时的速率
粒子初速度为零
粒子经电场加速
典例精析
例2.一个质量为m、电荷量为q的粒子,从容器下方的小孔S1飘入电势差为U的加速电场,然后经过S3沿着与磁场垂直的方向进入磁感应强度为B的匀强磁场中,最后打到照相底片D上求:
(2)求粒子在磁场中运动的轨道半径
粒子在磁场中做圆周运动,洛伦兹力提供向心力
典例精析
三、回旋加速器
1、直线加速器
原理:利用加速电场对带电粒子做正功使带电粒子的动能增加Ek=qU
由动能定理得带电粒子经几级的电场加速后增加的动能为Ek=q(
U1+U2+U3+··········+Un
)
新课教学
若需要很大的动能的粒子,利用直线加速器是否方便?为什么?那应该怎么办?
2、回旋加速器
(1)构造
新课教学
3、带电粒子的最终能量
当带电粒子的速度最大时,其在磁场中的转动半径也最大,由r=mv/qB知道v=qBr/m
若D形盒的半径为R时,带电粒子的出射速度变为v=qBR/m
所以,带电粒子的最终动能为
即粒子的最终动能由磁感应强度B和D形盒的半径R决定
新课教学
4、交流电的周期:
交流电的周期与粒子在磁场中做圆周运动周期
例3.
回旋加速器盒内的狭缝中有匀强电场,使粒子每次穿过狭缝时都得到加速,两盒放在磁感应强度为B的匀强磁场中,磁场方向垂直于盒底面,粒子源射出的粒子电荷量为q,质量为m,粒子最大回旋半径为R.
(1)粒子在盒内做何种运动;
(2)所加交变电流频率及粒子角速度;
(3)粒子离开加速器时的最大速度及最大动能.
典例精析
例3.
题目已知粒子电荷量为q,质量为m,粒子最大回旋半径为R.
(1)粒子在盒内做何种运动;
答案:带电粒子在盒内在洛伦兹力作用下做匀速圆周运动,每次加速之后半径变大.
典例精析
例3.题目已知粒子电荷量为q,质量为m,粒子最大回旋半径为R.
(2)所加交变电流频率及粒子角速度
提示:交流电的周期等于粒子做圆周运动的周期
解析:(2)
高频交变电流频率要等于粒子回旋频率,因为T=,回旋频率f==,角速度ω=2πf=.
典例精析
例3.题目已知粒子电荷量为q,质量为m,粒子最大回旋半径为R.
(3)粒子离开加速器时的最大速度及最大动能
提示:粒子运动半径等于D形盒时,速度最大,动能最大
解析:(3)由牛顿第二定律知=qBvmax
则Rmax=,vmax=
最大动能Ekmax=m=
典例精析
例4.已知氢核与氦核的质量之比m1∶m2=1∶4,电荷量之比q1∶q2=1∶2,当氢核与氦核以v1∶v2=4∶1的速度,垂直于磁场方向射入磁场后,分别做匀速圆周运动,则氢核与氦核半径之比r1∶r2=________,周期之比T1∶T2=________.
典例精析
由洛伦兹力提供向心力确定半径大小
利用周期公式分析求解
例4.已知:
质量之比m1∶m2=1∶4,
电荷量之比q1∶q2=1∶2,
速度之比v1∶v2=4∶1
求:
半径之比r1∶r2
周期之比T1∶T2
典例精析
答案 2∶1 1∶2
1.两个粒子,电荷量相等,在同一匀强磁场中只受磁场力而做匀速圆周运动( )
A.若速率相等,则半径必相等
B.若质量相等,则周期必相等
C.若周期相等,则半径必相等
D.若动能相等,则半径必相等
答案:B
课堂练习
2.在回旋加速器中( )
A.电场用来加速带电粒子,磁场则使带电粒子回旋
B.电场和磁场同时用来加速带电粒子
C.磁场相同的条件下,回旋加速器的半径越大,则带电粒子获得的动能越大
D.同一带电粒子获得的最大动能只与交流电压的大小有关,而与交流电压的频率无关
答案 AC
课堂练习
3.如图所示,有界匀强磁场边界线SP∥MN,速率不同的同种带电粒子从S点沿SP方向同时射入磁场.其中穿过a点的粒子速度v1与MN垂直;穿过b点的粒子速度v2与MN成60°角,设粒子从S到a、b所需时间分别为t1和t2,则t1∶t2为(重力不计)
( )
A.1∶3
B.4∶3
C.1∶1
D.3∶2
答案 D
课堂练习
4、如图所示,在第Ⅰ象限内有垂直于纸面向里的匀强磁场,一对正、负电子分别以相同速率以与x轴成30°的方向从原点射入磁场,则正、负电子在磁场中运动的时间之比为( )
A.1∶2 B.2∶1
C.1∶
D.1∶1
课堂练习
解析:由T=
可知,正、负电子
的运动周期相同
作出正、负电子运动轨迹如图所示,
正电子运动的圆心角等于120°
负电子运动的圆心角等于60°
由t=,得t正∶t负=θ正∶θ负=2∶1
故B正确.
答案:B
课堂练习
同课章节目录
- 第一章 电场
- 第01节 认识电场
- 第02节 探究静电力
- 第03节 电场强度
- 第04节 电势和电势差
- 第05节 电场强度与电势差的关系
- 第06节 示波器的奥秘
- 第07节 了解电容器
- 第08节 静电与新技术
- 第二章 电路
- 第01节 探究决定导线电阻的因素
- 第02节 对电阻的进一步研究
- 第03节 研究闭合电路
- 第04节 认识多用电表
- 第05节 电功率
- 第06节 走进门电路
- 第07节 了解集成电路
- 8.多用电表
- 9.实验:测定电池的电动势和内阻
- 10.简单的逻辑电路
- 第三章 磁场
- 第01节 我们周围的磁象
- 第02节 认识磁场
- 第03节 探究安培力
- 第04节 安培力的应用
- 第05节 研究洛仑兹力
- 第06节 洛仑兹力与现代技术
