高一数学人教版A版必修二课件:第四章 圆与方程章末复习课 课件(共36张PPT)
文档属性
| 名称 | 高一数学人教版A版必修二课件:第四章 圆与方程章末复习课 课件(共36张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-24 18:20:24 | ||
图片预览









文档简介
章末复习课
第四章 圆与方程
1.整合知识结构,梳理知识网络,进一步巩固、深化所学知识;
2.培养综合运用知识解决问题的能力,能灵活、熟练运用系数法求解圆的方程,能解决直线与圆的综合问题,渗透数形结合的数学思想.
要点归纳
题型探究
达标检测
学习目标
要点归纳 主干梳理 点点落实
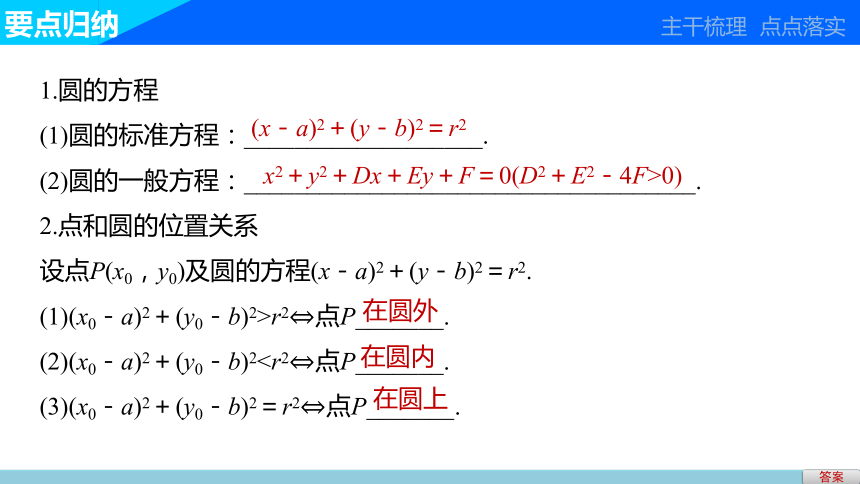
1.圆的方程
(1)圆的标准方程:___________________.
(2)圆的一般方程:____________________________________.
2.点和圆的位置关系
设点P(x0,y0)及圆的方程(x-a)2+(y-b)2=r2.
(1)(x0-a)2+(y0-b)2>r2?点P_______.
(2)(x0-a)2+(y0-b)2(3)(x0-a)2+(y0-b)2=r2?点P_______.
答案
(x-a)2+(y-b)2=r2
x2+y2+Dx+Ey+F=0(D2+E2-4F>0)
在圆外
在圆内
在圆上
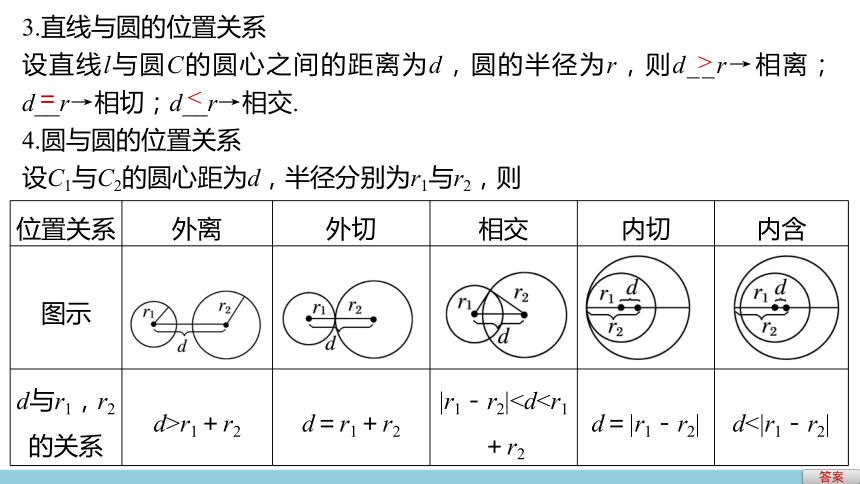
3.直线与圆的位置关系
设直线l与圆C的圆心之间的距离为d,圆的半径为r,则d__r→相离;d__r→相切;d__r→相交.
4.圆与圆的位置关系
设C1与C2的圆心距为d,半径分别为r1与r2,则
答案
位置关系
外离
外切
相交
内切
内含
图示
d与r1,r2的关系
d>r1+r2
d=r1+r2
|r1-r2|d=|r1-r2|
d<|r1-r2|
>
=
<
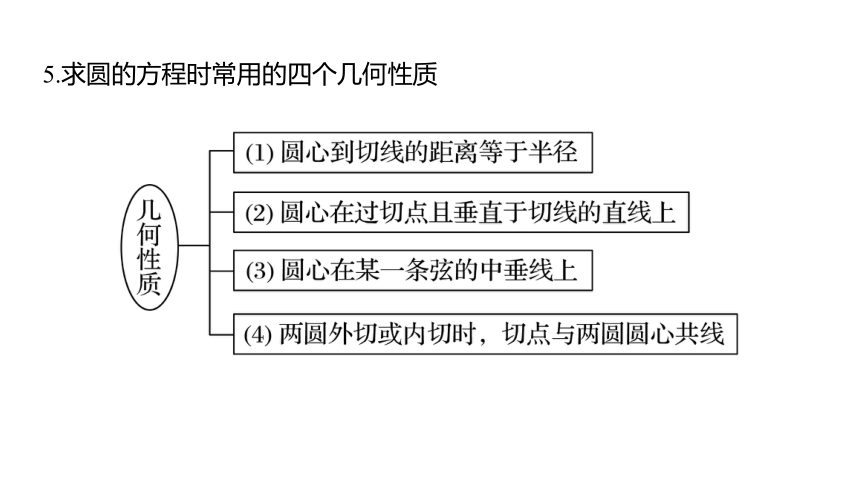
5.求圆的方程时常用的四个几何性质
(3)形如(x-a)2+(y-b)2形式的最值问题,可转化为动点到定点的距离的平方的最值问题.
7.计算直线被圆截得的弦长的常用方法
(1)几何方法
运用弦心距(即圆心到直线的距离)、弦长的一半及半径构成直角三角形计算.
6.与圆有关的最值问题的常见类型
返回
类型一 求圆的方程
题型探究 重点难点 个个击破
例1 根据条件求下列圆的方程:
(1)求经过A(6,5),B(0,1)两点,并且圆心在直线3x+10y+9=0上的圆的方程;
解 由题意知线段AB的垂直平分线方程为3x+2y-15=0,
解析答案
∴所求圆的方程为(x-7)2+(y+3)2=65.
解析答案
反思与感悟
解析答案
解 方法一 设圆的方程为(x-a)2+(y-b)2=r2,
∴(a-b)2=4,
又∵b=2a,∴a=2,b=4或a=-2,b=-4,
故所求圆的方程是(x-2)2+(y-4)2=10或(x+2)2+(y+4)2=10.
反思与感悟
解析答案
解 方法二 设圆的方程为(x-a)2+(y-b)2=10,
∵圆心C(a,b)在直线y=2x上,∴b=2a.
由圆被直线x-y=0截得的弦长为
将y=x代入(x-a)2+(y-b)2=10,
得2x2-2(a+b)x+a2+b2-10=0.
设直线y=x交圆C于A(x1,y1),B(x2,y2),
∴(x1+x2)2-4x1x2=16.
反思与感悟
反思与感悟
∴所求圆的方程为(x-2)2+(y-4)2=10或(x+2)2+(y+4)2=10.
反思与感悟
求圆的方程主要是根据圆的标准方程和一般方程,
利用待定系数法求解,采用待定系数法求圆的方程的一般步骤为
第一步:选择圆的方程的某一形式;
第二步:由题意得a,b,r(或D,E,F)的方程(组);
第三步:解出a,b,r(或D,E,F);
第四步:代入圆的方程.
注:解题时充分利用圆的几何性质可获得解题途径,减少运算量,
例如:圆的切线垂直于经过切点的半径;圆心与弦的中点连线垂直于弦;两圆相交时,连心线垂直平分两圆的公共弦;两圆相切时,连心线过切点等.
跟踪训练1 求圆心在直线y=-4x上,且与直线l:x+y-1=0相切于点P(3,-2)的圆的方程.
解析答案
解 方法一 设所求圆的标准方程为(x-a)2+(y-b)2=r2(r>0),
解得a=1,b=-4,r= ,
故所求圆的方程为(x-1)2+(y+4)2=8.
方法二 过切点且与x+y-1=0垂直的直线为y+2=x-3,
与y=-4x联立可求得圆心为(1,-4).
于是所求圆的方程为(x-1)2+(y+4)2=8.
类型二 直线与圆、圆与圆的位置关系
例2 已知点P(0,5)及圆C:x2+y2+4x-12y+24=0.若直线l过点P,且被圆C截得的线段长为 ,求l的方程.
解析答案
反思与感悟
解 如图所示,|AB|= ,设D是线段AB的中点,则CD⊥AB,
在Rt△ACD中,可得|CD|=2.
设所求直线l的斜率为k,则直线l的方程为y-5=kx,
即kx-y+5=0.由点C到直线AB的距离公式:
此时直线l的方程为3x-4y+20=0.
又∵直线l的斜率不存在时,也满足题意,此时方程为x=0.
∴所求直线l的方程为x=0或3x-4y+20=0.
反思与感悟
反思与感悟
直线与圆相交时,常涉及到弦长问题,弦长的计算有以下两种思路:
(1)代数方法:将直线和圆的方程联立得方程组,消元后得到一个一元二次方程,在判别式Δ>0的前提下,可利用根与系数的关系求弦长.
解决直线与圆相交问题时,常利用几何方法,即构造直角三角形,利用勾股定理,直线与圆相切时,圆心到直线的距离等于半径,圆心和切点的连线垂直于切线.
解 设所求圆C的方程为(x-a)2+(y-b)2=r2,
解析答案
跟踪训练2 已知圆C与圆x2+y2-2x=0相外切,并且与直线x+ y=0相切于点Q(3,- ),求圆C的方程.
例3 设定点M(-3,4),动点N在圆x2+y2=4上运动,以OM、ON为两边作平行四边形MONP,求点P的轨迹.
类型三 与圆有关的轨迹问题
解析答案
反思与感悟
解 如图所示,设P(x,y),N(x0,y0),
由于平行四边形的对角线互相平分,
又N(x+3,y-4)在圆上,故(x+3)2+(y-4)2=4.
因此所求轨迹为圆:(x+3)2+(y-4)2=4,
反思与感悟
求与圆有关的轨迹问题时,根据题设条件的不同常采用以下方法:
(1)直接法:直接根据题目提供的条件列出方程.
(2)定义法:根据圆、直线等定义列方程.
(3)几何法:利用圆的几何性质列方程.
(4)代入法:找到要求点与已知点的关系,代入已知点满足的关系式等.
反思与感悟
跟踪训练3 已知圆x2+y2=4上一定点A(2,0),B(1,1)为圆内一点,P,Q为圆上的动点.
(1)求线段AP中点的轨迹方程;
解 设AP的中点为M(x,y),由中点坐标公式可知,P点坐标为(2x-2,2y).
因为P点在圆x2+y2=4上,
所以(2x-2)2+(2y)2=4,
故线段AP中点的轨迹方程为(x-1)2+y2=1.
解析答案
(2)若∠PBQ=90°,求线段PQ中点的轨迹方程.
解 设PQ的中点为N(x,y),连接BN.
在Rt△PBQ中,|PN|=|BN|.
设O为坐标原点,连接ON,则ON⊥PQ,
所以|OP|2=|ON|2+|PN|2=|ON|2+|BN|2,
所以x2+y2+(x-1)2+(y-1)2=4.
故线段PQ中点的轨迹方程为x2+y2-x-y-1=0.
解析答案
类型四 分类讨论在直线与圆中的应用
解析答案
例4 已知直线l经过点P(-4,-3),且被圆(x+1)2+(y+2)2=25截得的弦长为8,求直线l的方程.
解 圆(x+1)2+(y+2)2=25的圆心为(-1,-2),半径r=5,
①当直线l的斜率不存在时,其方程为x=-4,由题意可知直线x=-4符合题意.
②当直线l的斜率存在时,设其方程为y+3=k(x+4),即kx-y+4k-3=0.
即所求直线方程为4x+3y+25=0,
综上所述,满足题设的直线l方程为x=-4或4x+3y+25=0.
在用二元二次方程表示圆时要分类讨论,在求直线方程时,根据题意不确定斜率是否存在,要分斜率存在与斜率不存在这两种情况进行分类讨论.
反思与感悟
解析答案
跟踪训练4 过点A(4,-3)作圆C:(x-3)2+(y-1)2=1的切线,求此切线方程.
返回
解 ∵(4-3)2+(-3-1)2=17>1,
∴点A在圆外.
①若所求直线的斜率存在,
设切线斜率为k,则切线方程为y+3=k(x-4),
因为圆心C(3,1)到切线的距离等于半径1,
②若切线斜率不存在,圆心C(3,1)到直线x=4的距离也为1,
这时直线与圆也相切,所以另一条切线方程是x=4.
综上,所求切线方程为15x+8y-36=0或x=4.
返回
1
2
3
达标检测
解析答案
1.如图,已知圆C与x轴相切于点T(1,0),与y轴正半轴交于两点A,B(B在A的上方),且|AB|=2,则
(1)圆C的标准方程为_____________________.
4
(2)圆C在点B处的切线在x轴上的截距为________.
解析 令x=0得:B(0, +1).
1
2
3
4
解析答案
解析答案
2.已知圆M:(x-1)2+(y-1)2=4,直线l过点P(2,3)且与圆M交于A,B两点,且|AB|=2,则直线l的方程为________________________.
1
2
3
4
1
2
3
4
解析 (1)当直线l的斜率存在时,
设直线l的方程为y-3=k(x-2),即kx-y+3-2k=0.
作示意图如图,MC⊥AB于C.
故直线l的方程为3x-4y+6=0.
(2)当直线l的斜率不存在时,其方程为x=2,
综上所述,直线l的方程为3x-4y+6=0或x=2.
解析答案
3.圆x2+y2=4上的点到直线x-y+2=0的距离的最大值为________.
1
2
3
4
解析答案
1
2
3
4
解 设方程(x-3)2+(y-3)2=6上的任意一点P(x,y).
由图可知,当直线OP与圆相切时,斜率取最值.
规律与方法
初中我们从平面几何的角度研究过圆的问题,本章则主要是利用圆的方程从代数角度研究了圆的性质,如果我们能够将两者有机地结合起来解决圆的问题,将在处理圆的有关问题时收到意想不到的效果.
圆是非常特殊的几何图形,它既是中心对称图形又是轴对称图形,它的许多几何性质在解决圆的问题时往往起到事半功倍的作用,所以在实际解题中常用几何法,充分结合圆的平面几何性质.那么,经常使用的几何性质有
(1)圆的切线的性质:圆心到切线的距离等于半径;切点与圆心的连线垂直于切线;切线在切点处的垂线一定经过圆心;圆心、圆外一点及该点所引切线的切点构成直角三角形的三个顶点等等.
(2)直线与圆相交的弦的有关性质:相交弦的中点与圆心的连线垂直于弦所在直线;弦的垂直平分线(中垂线)一定经过圆心;弦心距、半径、弦长的一半构成直角三角形的三边,满足勾股定理.
(3)与直径有关的几何性质:直径是圆的最长的弦;圆的对称轴一定经过圆心;直径所对的圆周角是直角.
返回
第四章 圆与方程
1.整合知识结构,梳理知识网络,进一步巩固、深化所学知识;
2.培养综合运用知识解决问题的能力,能灵活、熟练运用系数法求解圆的方程,能解决直线与圆的综合问题,渗透数形结合的数学思想.
要点归纳
题型探究
达标检测
学习目标
要点归纳 主干梳理 点点落实
1.圆的方程
(1)圆的标准方程:___________________.
(2)圆的一般方程:____________________________________.
2.点和圆的位置关系
设点P(x0,y0)及圆的方程(x-a)2+(y-b)2=r2.
(1)(x0-a)2+(y0-b)2>r2?点P_______.
(2)(x0-a)2+(y0-b)2
答案
(x-a)2+(y-b)2=r2
x2+y2+Dx+Ey+F=0(D2+E2-4F>0)
在圆外
在圆内
在圆上
3.直线与圆的位置关系
设直线l与圆C的圆心之间的距离为d,圆的半径为r,则d__r→相离;d__r→相切;d__r→相交.
4.圆与圆的位置关系
设C1与C2的圆心距为d,半径分别为r1与r2,则
答案
位置关系
外离
外切
相交
内切
内含
图示
d与r1,r2的关系
d>r1+r2
d=r1+r2
|r1-r2|
d<|r1-r2|
>
=
<
5.求圆的方程时常用的四个几何性质
(3)形如(x-a)2+(y-b)2形式的最值问题,可转化为动点到定点的距离的平方的最值问题.
7.计算直线被圆截得的弦长的常用方法
(1)几何方法
运用弦心距(即圆心到直线的距离)、弦长的一半及半径构成直角三角形计算.
6.与圆有关的最值问题的常见类型
返回
类型一 求圆的方程
题型探究 重点难点 个个击破
例1 根据条件求下列圆的方程:
(1)求经过A(6,5),B(0,1)两点,并且圆心在直线3x+10y+9=0上的圆的方程;
解 由题意知线段AB的垂直平分线方程为3x+2y-15=0,
解析答案
∴所求圆的方程为(x-7)2+(y+3)2=65.
解析答案
反思与感悟
解析答案
解 方法一 设圆的方程为(x-a)2+(y-b)2=r2,
∴(a-b)2=4,
又∵b=2a,∴a=2,b=4或a=-2,b=-4,
故所求圆的方程是(x-2)2+(y-4)2=10或(x+2)2+(y+4)2=10.
反思与感悟
解析答案
解 方法二 设圆的方程为(x-a)2+(y-b)2=10,
∵圆心C(a,b)在直线y=2x上,∴b=2a.
由圆被直线x-y=0截得的弦长为
将y=x代入(x-a)2+(y-b)2=10,
得2x2-2(a+b)x+a2+b2-10=0.
设直线y=x交圆C于A(x1,y1),B(x2,y2),
∴(x1+x2)2-4x1x2=16.
反思与感悟
反思与感悟
∴所求圆的方程为(x-2)2+(y-4)2=10或(x+2)2+(y+4)2=10.
反思与感悟
求圆的方程主要是根据圆的标准方程和一般方程,
利用待定系数法求解,采用待定系数法求圆的方程的一般步骤为
第一步:选择圆的方程的某一形式;
第二步:由题意得a,b,r(或D,E,F)的方程(组);
第三步:解出a,b,r(或D,E,F);
第四步:代入圆的方程.
注:解题时充分利用圆的几何性质可获得解题途径,减少运算量,
例如:圆的切线垂直于经过切点的半径;圆心与弦的中点连线垂直于弦;两圆相交时,连心线垂直平分两圆的公共弦;两圆相切时,连心线过切点等.
跟踪训练1 求圆心在直线y=-4x上,且与直线l:x+y-1=0相切于点P(3,-2)的圆的方程.
解析答案
解 方法一 设所求圆的标准方程为(x-a)2+(y-b)2=r2(r>0),
解得a=1,b=-4,r= ,
故所求圆的方程为(x-1)2+(y+4)2=8.
方法二 过切点且与x+y-1=0垂直的直线为y+2=x-3,
与y=-4x联立可求得圆心为(1,-4).
于是所求圆的方程为(x-1)2+(y+4)2=8.
类型二 直线与圆、圆与圆的位置关系
例2 已知点P(0,5)及圆C:x2+y2+4x-12y+24=0.若直线l过点P,且被圆C截得的线段长为 ,求l的方程.
解析答案
反思与感悟
解 如图所示,|AB|= ,设D是线段AB的中点,则CD⊥AB,
在Rt△ACD中,可得|CD|=2.
设所求直线l的斜率为k,则直线l的方程为y-5=kx,
即kx-y+5=0.由点C到直线AB的距离公式:
此时直线l的方程为3x-4y+20=0.
又∵直线l的斜率不存在时,也满足题意,此时方程为x=0.
∴所求直线l的方程为x=0或3x-4y+20=0.
反思与感悟
反思与感悟
直线与圆相交时,常涉及到弦长问题,弦长的计算有以下两种思路:
(1)代数方法:将直线和圆的方程联立得方程组,消元后得到一个一元二次方程,在判别式Δ>0的前提下,可利用根与系数的关系求弦长.
解决直线与圆相交问题时,常利用几何方法,即构造直角三角形,利用勾股定理,直线与圆相切时,圆心到直线的距离等于半径,圆心和切点的连线垂直于切线.
解 设所求圆C的方程为(x-a)2+(y-b)2=r2,
解析答案
跟踪训练2 已知圆C与圆x2+y2-2x=0相外切,并且与直线x+ y=0相切于点Q(3,- ),求圆C的方程.
例3 设定点M(-3,4),动点N在圆x2+y2=4上运动,以OM、ON为两边作平行四边形MONP,求点P的轨迹.
类型三 与圆有关的轨迹问题
解析答案
反思与感悟
解 如图所示,设P(x,y),N(x0,y0),
由于平行四边形的对角线互相平分,
又N(x+3,y-4)在圆上,故(x+3)2+(y-4)2=4.
因此所求轨迹为圆:(x+3)2+(y-4)2=4,
反思与感悟
求与圆有关的轨迹问题时,根据题设条件的不同常采用以下方法:
(1)直接法:直接根据题目提供的条件列出方程.
(2)定义法:根据圆、直线等定义列方程.
(3)几何法:利用圆的几何性质列方程.
(4)代入法:找到要求点与已知点的关系,代入已知点满足的关系式等.
反思与感悟
跟踪训练3 已知圆x2+y2=4上一定点A(2,0),B(1,1)为圆内一点,P,Q为圆上的动点.
(1)求线段AP中点的轨迹方程;
解 设AP的中点为M(x,y),由中点坐标公式可知,P点坐标为(2x-2,2y).
因为P点在圆x2+y2=4上,
所以(2x-2)2+(2y)2=4,
故线段AP中点的轨迹方程为(x-1)2+y2=1.
解析答案
(2)若∠PBQ=90°,求线段PQ中点的轨迹方程.
解 设PQ的中点为N(x,y),连接BN.
在Rt△PBQ中,|PN|=|BN|.
设O为坐标原点,连接ON,则ON⊥PQ,
所以|OP|2=|ON|2+|PN|2=|ON|2+|BN|2,
所以x2+y2+(x-1)2+(y-1)2=4.
故线段PQ中点的轨迹方程为x2+y2-x-y-1=0.
解析答案
类型四 分类讨论在直线与圆中的应用
解析答案
例4 已知直线l经过点P(-4,-3),且被圆(x+1)2+(y+2)2=25截得的弦长为8,求直线l的方程.
解 圆(x+1)2+(y+2)2=25的圆心为(-1,-2),半径r=5,
①当直线l的斜率不存在时,其方程为x=-4,由题意可知直线x=-4符合题意.
②当直线l的斜率存在时,设其方程为y+3=k(x+4),即kx-y+4k-3=0.
即所求直线方程为4x+3y+25=0,
综上所述,满足题设的直线l方程为x=-4或4x+3y+25=0.
在用二元二次方程表示圆时要分类讨论,在求直线方程时,根据题意不确定斜率是否存在,要分斜率存在与斜率不存在这两种情况进行分类讨论.
反思与感悟
解析答案
跟踪训练4 过点A(4,-3)作圆C:(x-3)2+(y-1)2=1的切线,求此切线方程.
返回
解 ∵(4-3)2+(-3-1)2=17>1,
∴点A在圆外.
①若所求直线的斜率存在,
设切线斜率为k,则切线方程为y+3=k(x-4),
因为圆心C(3,1)到切线的距离等于半径1,
②若切线斜率不存在,圆心C(3,1)到直线x=4的距离也为1,
这时直线与圆也相切,所以另一条切线方程是x=4.
综上,所求切线方程为15x+8y-36=0或x=4.
返回
1
2
3
达标检测
解析答案
1.如图,已知圆C与x轴相切于点T(1,0),与y轴正半轴交于两点A,B(B在A的上方),且|AB|=2,则
(1)圆C的标准方程为_____________________.
4
(2)圆C在点B处的切线在x轴上的截距为________.
解析 令x=0得:B(0, +1).
1
2
3
4
解析答案
解析答案
2.已知圆M:(x-1)2+(y-1)2=4,直线l过点P(2,3)且与圆M交于A,B两点,且|AB|=2,则直线l的方程为________________________.
1
2
3
4
1
2
3
4
解析 (1)当直线l的斜率存在时,
设直线l的方程为y-3=k(x-2),即kx-y+3-2k=0.
作示意图如图,MC⊥AB于C.
故直线l的方程为3x-4y+6=0.
(2)当直线l的斜率不存在时,其方程为x=2,
综上所述,直线l的方程为3x-4y+6=0或x=2.
解析答案
3.圆x2+y2=4上的点到直线x-y+2=0的距离的最大值为________.
1
2
3
4
解析答案
1
2
3
4
解 设方程(x-3)2+(y-3)2=6上的任意一点P(x,y).
由图可知,当直线OP与圆相切时,斜率取最值.
规律与方法
初中我们从平面几何的角度研究过圆的问题,本章则主要是利用圆的方程从代数角度研究了圆的性质,如果我们能够将两者有机地结合起来解决圆的问题,将在处理圆的有关问题时收到意想不到的效果.
圆是非常特殊的几何图形,它既是中心对称图形又是轴对称图形,它的许多几何性质在解决圆的问题时往往起到事半功倍的作用,所以在实际解题中常用几何法,充分结合圆的平面几何性质.那么,经常使用的几何性质有
(1)圆的切线的性质:圆心到切线的距离等于半径;切点与圆心的连线垂直于切线;切线在切点处的垂线一定经过圆心;圆心、圆外一点及该点所引切线的切点构成直角三角形的三个顶点等等.
(2)直线与圆相交的弦的有关性质:相交弦的中点与圆心的连线垂直于弦所在直线;弦的垂直平分线(中垂线)一定经过圆心;弦心距、半径、弦长的一半构成直角三角形的三边,满足勾股定理.
(3)与直径有关的几何性质:直径是圆的最长的弦;圆的对称轴一定经过圆心;直径所对的圆周角是直角.
返回
