高一数学人教版A版必修二课件:第二章 点、直线、平面之间的位置关系章末复习课 课件(共45张PPT)
文档属性
| 名称 | 高一数学人教版A版必修二课件:第二章 点、直线、平面之间的位置关系章末复习课 课件(共45张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-24 00:00:00 | ||
图片预览






文档简介
章末复习课
第二章 点、直线、平面之间的位置关系
1.整合知识结构,梳理各知识网络,进一步巩固、深化所学知识;
2.提高综合运用知识的能力和空间想象能力,在空间实现平行关系、垂直关系、垂直与平行关系之间的转化.
要点归纳
题型探究
达标检测
学习目标
要点归纳 主干梳理 点点落实
1.四个公理
公理1:如果一条直线上的______在一个平面内,那么这条直线上所有的点都在这个平面内.
公理2:过__________________的三点,有且只有一个平面.
公理3:如果两个不重合的平面有一个公共点,那么它们有且只有_____________________.
公理4:平行于同一条直线的两条直线互相_____.
2.直线与直线的位置关系
答案
————
共面直线
异面直线:不同在_____一个平面内,没有公共点
两点
不在同一条直线上
一条过该点的公共直线
平行
平行
相交
任何
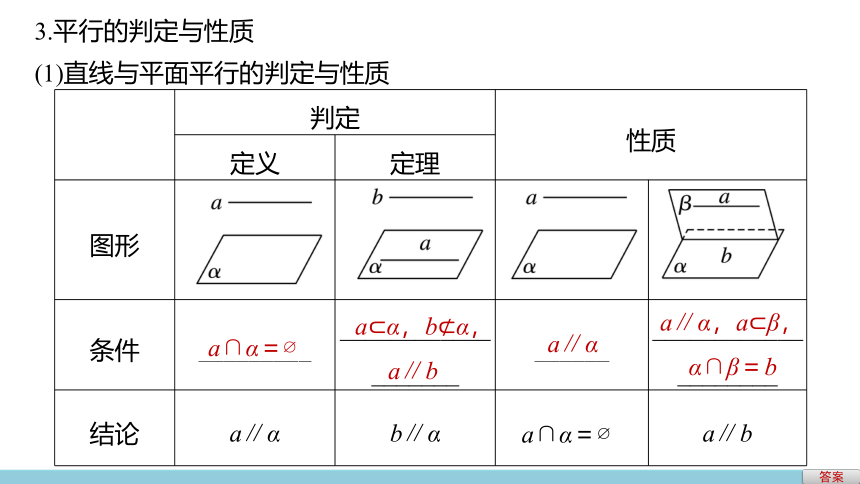
3.平行的判定与性质
(1)直线与平面平行的判定与性质
答案
?
判定
性质
定义
定理
图形
条件
_________
___________________
______
____________________
结论
a∥α
b∥α
a∩α=?
a∥b
a∩α=?
a?α,b?α,
a∥b
a∥α
a∥α,a?β,
α∩β=b
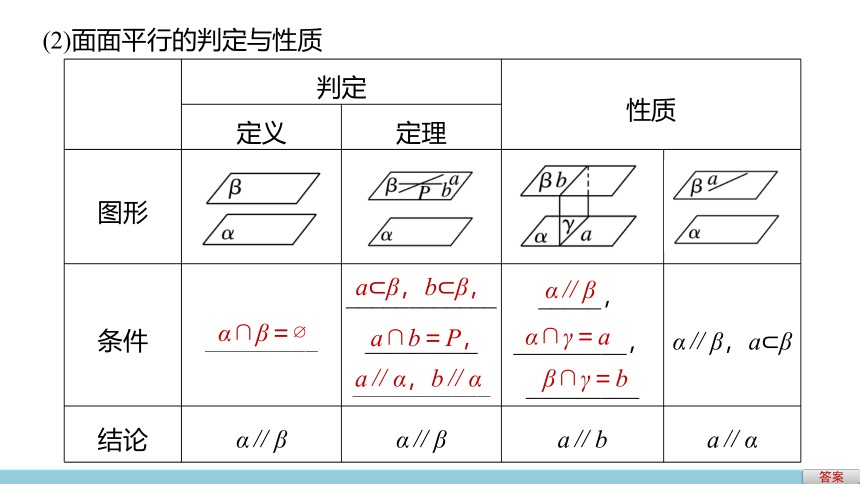
(2)面面平行的判定与性质
答案
?
判定
性质
定义
定理
图形
条件
_________
_____________________
___________
_____,_________,_________
α∥β,a?β
结论
α∥β
α∥β
a∥b
a∥α
α∩β=?
a?β,b?β,
a∩b=P,
a∥α,b∥α
α∥β
β∩γ=b
α∩γ=a
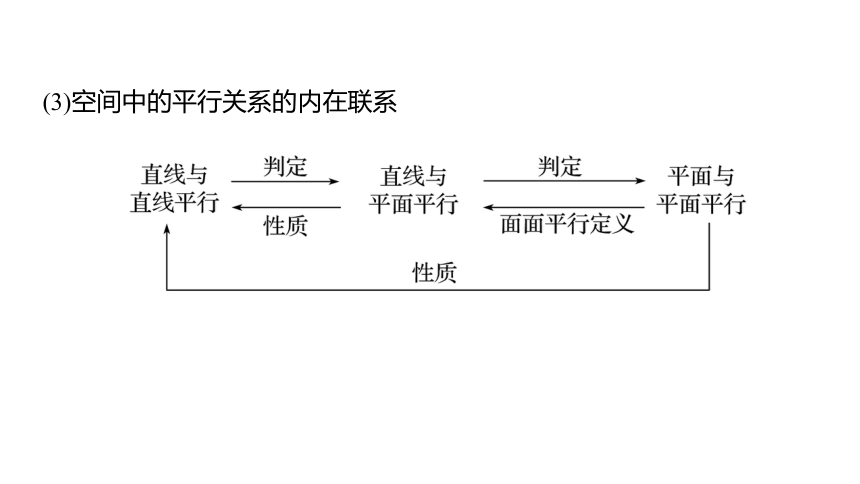
(3)空间中的平行关系的内在联系
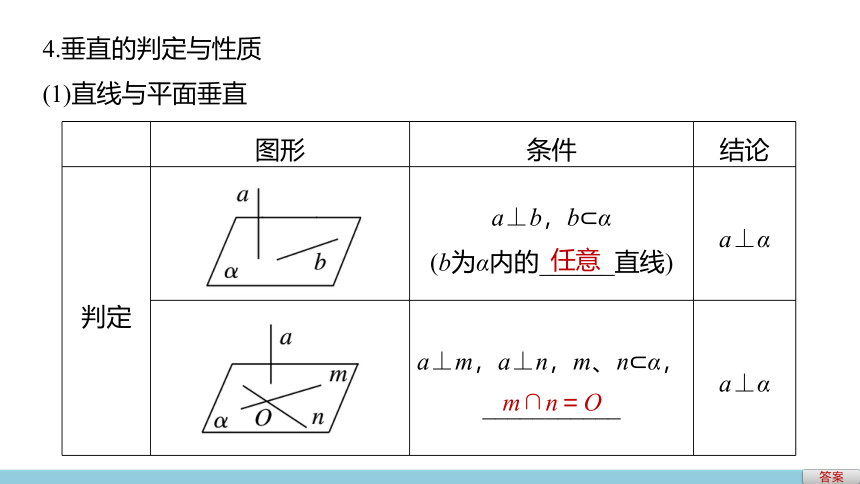
4.垂直的判定与性质
(1)直线与平面垂直
答案
?
图形
条件
结论
判定
a⊥b,b?α
(b为α内的______直线)
a⊥α
a⊥m,a⊥n,m、n?α,___________
a⊥α
任意
m∩n=O
答案
判定
a∥b,______
b⊥α
性质
a⊥α,______
a⊥b
a⊥α,b⊥α
______
a⊥α
b?α
a∥b
(2)平面与平面垂直的判定与性质定理
?
文字语言
图形语言
符号语言
判定定理
如果一个平面经过另一个平面的一条_____,那么这两个平面互相垂直
?α⊥β
性质定理
如果两个平面互相垂直,那么在一个平面内垂直于它们交线的直线垂直于另一个平面
?l⊥α
α⊥β,
α∩β=a,
l?β,
l⊥a
垂线
答案
(3)空间中的垂直关系的内在联系.
答案
5.空间角
(1)异面直线所成的角
①定义:设a,b是两条异面直线,经过空间任一点O作直线a′∥a,b′∥b,把a′与b′所成的_____________叫做异面直线a,b所成的角(或夹角).
②范围:设两异面直线所成角为θ,则0°<θ≤90°.
锐角(或直角)
(2)直线和平面所成的角
①平面的一条斜线与它在______________所成的锐角叫做这条直线与这个平面所成的角.
②当直线与平面垂直和平行(或直线在平面内)时,规定直线和平面所成的角分别为__________.
(3)二面角的有关概念
①二面角:从一条直线和由这条直线出发的_____________所组成的图形叫做二面角.
②二面角的平面角:以二面角的棱上任意一点为端点,在两个半平面内分别作_________的两条射线,这两条射线所成的角叫做二面角的平面角.
返回
答案
平面内的射影
90°和0°
两个半平面
垂直于棱
类型一 几何中共点、共线、共面问题
题型探究 重点难点 个个击破
例1 如图所示,空间四边形ABCD中,E,F分别为AB,AD的中点,G,H分别在BC,CD上,且BG∶GC=DH∶HC=1∶2.
求证:(1)E、F、G、H四点共面;
证明 ∵BG∶GC=DH∶HC,∴GH∥BD,
又EF∥BD,∴EF∥GH,
∴E、F、G、H四点共面.
解析答案
(2)GE与HF的交点在直线AC上.
证明 ∵G、H不是BC、CD的中点,∴EF≠GH.
又EF∥GH,∴EG与FH不平行,
则必相交,设交点为M.
反思与感悟
?M在面ABC与面ACD的交线上,
又面ABC∩面ACD=AC?M∈AC.
∴GE与HF的交点在直线AC上.
解析答案
反思与感悟
1.证明共面问题
证明共面问题,一般有两种证法:一是由某些元素确定一个平面,再证明其余元素在这个平面内;二是分别由不同元素确定若干个平面,再证明这些平面重合.
2.证明三点共线问题
证明空间三点共线问题,通常证明这些点都在两个面的交线上,即先确定出某两点在某两个平面的交线上,再证明第三个点是两个平面的公共点,当然必在两个平面的交线上.
3.证明三线共点问题
证明空间三线共点问题,先证两条直线交于一点,再证明第三条直线经过这点,把问题转化为证明点在直线上的问题.
跟踪训练1 如图,O是正方体ABCD-A1B1C1D1上底面ABCD的中心,M是正方体对角线AC1和截面A1BD的交点.求证:O、M、A1三点共线.
证明 ∵O∈AC,AC?平面ACC1A1,∴O∈平面ACC1A1.
∵M∈AC1,AC1?平面ACC1A1,∴M∈平面ACC1A1.
又已知A1∈平面ACC1A1,
即有O、M、A1三点都在平面ACC1A1上,
又O、M、A1三点都在平面A1BD上,
所以O、M、A1三点都在平面ACC1A1与平面A1BD的交线上,
所以O、M、A1三点共线.
解析答案
类型二 空间中的平行关系
例2 如图,E、F、G、H分别是正方体ABCD—A1B1C1D1的棱BC、CC1、C1D1、AA1的中点,
求证:(1)GE∥平面BB1D1D;
证明 如图,取B1D1中点O,连接GO,OB,
解析答案
∴OG綊BE,四边形BEGO为平行四边形.
∴OB∥GE.
∵OB?平面BDD1B1,GE?平面BDD1B1,
∴GE∥平面BDD1B1.
(2)平面BDF∥平面B1D1H.
证明 由正方体性质得B1D1∥BD,
∵B1D1?平面BDF,BD?平面BDF,
∴B1D1∥平面BDF.
连接HB,D1F,易证HBFD1是平行四边形,得HD1∥BF.
∵HD1?平面BDF,BF?平面BDF,
∴HD1∥平面BDF.
∵B1D1∩HD1=D1,
∴平面BDF∥平面B1D1H.
解析答案
反思与感悟
反思与感悟
1.判断线面平行的两种常用方法
面面平行判定的落脚点是线面平行,因此掌握线面平行的判定方法是必要的,判定线面平行的两种方法:
(1)利用线面平行的判定定理.
(2)利用面面平行的性质,即当两平面平行时,其中一平面内的任一直线平行于另一平面.
2.判断面面平行的常用方法
(1)利用面面平行的判定定理.
(2)面面平行的传递性(α∥β,β∥γ?α∥γ);
(3)利用线面垂直的性质(l⊥α,l⊥β?α∥β).
跟踪训练2 如图,△ABC为正三角形,EC⊥平面ABC,DB⊥平面ABC,CE=CA=2BD,M是EA的中点,N是EC的中点,求证:平面DMN∥平面ABC.
证明 ∵M、N分别是EA与EC的中点,∴MN∥AC,
又∵AC?平面ABC,MN?平面ABC,∴MN∥平面ABC,
∵DB⊥平面ABC,EC⊥平面ABC,∴BD∥EC,
∵N为EC中点,EC=2BD,∴NC綊BD,
∴四边形BCND为矩形,∴DN∥BC,
又∵DN?平面ABC,BC?平面ABC,
∴DN∥平面ABC,
又∵MN∩DN=N,∴平面DMN∥平面ABC.
解析答案
例3 如图所示,在四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,E是PC的中点.
证明:(1)CD⊥AE;
证明 在四棱锥P-ABCD中,
∵PA⊥底面ABCD,CD?平面ABCD,∴PA⊥CD.
∵AC⊥CD,PA∩AC=A,∴CD⊥平面PAC.
而AE?平面PAC,∴CD⊥AE.
类型三 空间中的垂直关系
解析答案
(2)PD⊥平面ABE.
证明 由PA=AB=BC,∠ABC=60°,可得AC=PA.
∵E是PC的中点,∴AE⊥PC.
由(1),知AE⊥CD,且PC∩CD=C,∴AE⊥平面PCD.
而PD?平面PCD,∴AE⊥PD.
∵PA⊥底面ABCD,∴PA⊥AB.
又∵AB⊥AD且PA∩AD=A,
∴AB⊥平面PAD,而PD?平面PAD,
∴AB⊥PD.
又∵AB∩AE=A,∴PD⊥平面ABE.
解析答案
反思与感悟
空间垂直关系的判定方法
(1)判定线线垂直的方法:
①计算所成的角为90°(包括平面角和异面直线所成的角);
②线面垂直的性质(若a⊥α,b?α,则a⊥b).
(2)判定线面垂直的方法:
①线面垂直定义(一般不易验证任意性);
②线面垂直的判定定理(a⊥b,a⊥c,b?α,c?α,b∩c=M?a⊥α);
③平行线垂直平面的传递性质(a∥b,b⊥α?a⊥α);
④面面垂直的性质(α⊥β,α∩β=l,a?β,a⊥l?a⊥α);
⑤面面平行的性质(a⊥α,α∥β?a⊥β);
⑥面面垂直的性质(α∩β=l,α⊥γ,β⊥γ?l⊥γ).
反思与感悟
反思与感悟
(3)面面垂直的判定方法:
①根据定义(作两平面构成二面角的平面角,计算其为90°);
②面面垂直的判定定理(a⊥β,a?α?α⊥β).
跟踪训练3 如图,A,B,C,D为空间四点.在△ABC中,AB=2,
(1)当平面ADB⊥平面ABC时,求CD;
解 如图,取AB的中点E,连接DE,CE,
因为△ADB是等边三角形,所以DE⊥AB.
当平面ADB⊥平面ABC时,因为平面ADB∩平面ABC=AB,
所以DE⊥平面ABC,可知DE⊥CE,
解析答案
解 当△ADB以AB为轴转动时,总有AB⊥CD.
证明如下:①当D在平面ABC内时,
因为AC=BC,AD=BD,
所以C,D都在线段AB的垂直平分线上,即AB⊥CD.
②当D不在平面ABC内时,
由(1)知AB⊥DE.又因AC=BC,所以AB⊥CE.
又DE,CE为相交直线,所以AB⊥平面CDE,
由CD?平面CDE,得AB⊥CD.
综上所述,总有AB⊥CD.
解析答案
(2)当△ADB转动时,是否总有AB⊥CD?证明你的结论.
类型四 空间角问题
解析答案
例4 如图,在四棱锥P—ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,E是PC的中点.
(1)求PB和平面PAD所成的角的大小;
解 在四棱锥P—ABCD中,
因为PA⊥底面ABCD,AB?平面ABCD,
故PA⊥AB.又AB⊥AD,PA∩AD=A,
从而AB⊥平面PAD,故PB在平面PAD内的射影为PA,
从而∠APB为PB和平面PAD所成的角.
在Rt△PAB中,AB=PA,故∠APB=45°.
所以PB和平面PAD所成的角的大小为45°.
(2)证明:AE⊥平面PCD;
证明 在四棱锥P—ABCD中,
因为PA⊥底面ABCD,CD?平面ABCD,
故CD⊥PA.由条件CD⊥AC,PA∩AC=A,
所以CD⊥平面PAC.
又AE?平面PAC,所以AE⊥CD.
由PA=AB=BC,∠ABC=60°,可得AC=PA.
因为E是PC的中点,所以AE⊥PC.
又PC∩CD=C,所以AE⊥平面PCD.
解析答案
(3)求二面角A—PD—C的正弦值.
解析答案
反思与感悟
解 过点E作EM⊥PD,垂足为M,连接AM,如图所示.
由(2)知,AE⊥平面PCD,AM在平面PCD内的射影是EM,
则可证得AM⊥PD.
因此∠AME是二面角A—PD—C的平面角.
由已知,可得∠CAD=30°.
设AC=a,可得
在Rt△ADP中,∵AM⊥PD,∴AM·PD=PA·AD,
反思与感悟
1.求异面直线所成的角常用平移转化法(转化为相交直线的夹角).
2.求直线与平面所成的角常用射影转化法(即作垂线、找射影).
3.二面角的平面角的作法常有三种:(1)定义法;(2)垂线法;(3)垂面法.
反思与感悟
解析答案
跟踪训练4 如图,正方体的棱长为1,B′C∩BC′=O,求:
(1)AO与A′C′所成角的度数;
解 ∵A′C′∥AC,
∴AO与A′C′所成的角就是∠OAC.
∵AB⊥平面BC′,OC?平面BC′,
∴OC⊥AB,又OC⊥BO,AB∩BO=B.
∴OC⊥平面ABO.
又OA?平面ABO,∴OC⊥OA.
解析答案
(2)AO与平面ABCD所成角的正切值;
解 如图,作OE⊥BC于E,连接AE.
∵平面BC′⊥平面ABCD,
∴OE⊥平面ABCD,
∴∠OAE为OA与平面ABCD所成的角.
解析答案
(3)平面AOB与平面AOC所成角的度数.
解 ∵OC⊥OA,OC⊥OB,OA∩OB=O,
∴OC⊥平面AOB.
又∵OC?平面AOC,
∴平面AOB⊥平面AOC.
即平面AOB与平面AOC所成角的度数为90°.
返回
1
2
3
达标检测
解析答案
1.下列四个结论:
(1)两条直线都和同一个平面平行,则这两条直线平行.
(2)两条直线没有公共点,则这两条直线平行.
(3)两条直线都和第三条直线垂直,则这两条直线平行.
(4)一条直线和一个平面内无数条直线没有公共点,则这条直线和这个平面平行.
其中正确的个数为( )
A.0 B.1 C.2 D.3
4
解析 (1)两条直线都和同一个平面平行,这两条直线三种位置关系都有可能;
(2)两条直线没有公共点,则这两条直线平行或异面;
(3)两条直线都和第三条直线垂直,则这两条直线三种位置关系都有可能;
(4)一条直线和一个平面内无数条直线没有公共点,则这条直线也可在这个平面内.
答案 A
1
2
3
4
解析答案
2.设有不同的直线m、n和不同的平面α、β,下列四个命题中,正确的是( )
A.若m∥α,n∥α,则m∥n
B.若m?α,n?α,m∥β,n∥β,则α∥β
C.若α⊥β,m?α,则m⊥β
D.若α⊥β,m⊥β,m?α,则m∥α
1
2
3
4
解析 选项A中当m∥α,n∥α时,m与n可以平行、相交、异面;
选项B中满足条件的α与β可以平行,也可以相交;
选项C中,当α⊥β,m?α时,m与β可以垂直,也可以平行等.
故选项A、B、C均不正确.
D
解析答案
3.如图,已知正方体ABCD-A1B1C1D1,O是底面ABCD对角线的交点.
求证:(1)C1O∥面AB1D1;
证明 如图,连接A1C1,设A1C1∩B1D1=O1,连接AO1,
∵ABCD-A1B1C1D1是正方体,∴A1ACC1是平行四边形,
∴A1C1∥AC且A1C1=AC,
又O1,O分别是A1C1,AC的中点,
∴O1C1∥AO且O1C1=AO,
∴四边形AOC1O1是平行四边形,
∴C1O∥AO1,AO1?面AB1D1,C1O?面AB1D1,
∴C1O∥面AB1D1.
1
2
3
4
解析答案
(2)A1C⊥面AB1D1.
证明 ∵CC1⊥面A1B1C1D1,
∴CC1⊥B1D1,
又∵A1C1⊥B1D1,
∴B1D1⊥面A1C1CA,
即A1C⊥B1D1,同理可证A1C⊥AB1,
又B1D1∩AB1=B1,∴A1C⊥面AB1D1.
1
2
3
4
解析答案
1
2
3
4
4.如图,AB是⊙O的直径,PA垂直于⊙O所在的平面,C是圆周上不同于A,B的一动点.
(1)证明:△PBC是直角三角形.
解 因为AB是⊙O的直径,C是圆周上不同于A,
B的一动点,
所以BC⊥AC,
因为PA⊥平面ABC,所以BC⊥PA,
又PA∩AC=A,所以BC⊥平面PAC,
所以BC⊥PC,
所以△PBC是直角三角形.
1
2
3
4
(2)若PA=AB=2,且当直线PC与平面ABC所成角正切值为 时,求直线AB与平面PBC所成角的正弦值.
解析答案
1
2
3
4
解 如图,过A作AH⊥PC于H,连接BH,
因为BC⊥平面PAC,所以BC⊥AH,PC∩BC=C,
所以AH⊥平面PBC,所以∠ABH是直线AB与平面PBC所成角,
因为PA⊥平面ABC,所以∠PCA即是PC与平面ABC所成角,
规律与方法
一、平行关系
1.平行问题的转化关系
2.直线与平面平行的主要判定方法
(1)定义法;(2)判定定理;(3)面与面平行的性质.
3.平面与平面平行的主要判定方法
(1)定义法;(2)判定定理;(3)推论;
(4)a⊥α,a⊥β?α∥β.
二、垂直关系
1.空间中垂直关系的相互转化
2.判定线面垂直的常用方法
(1)利用线面垂直的判定定理.
(2)利用“两平行线中的一条与平面垂直,则另一条也与这个平面垂直”.
(3)利用“一条直线垂直于两平行平面中的一个,则与另一个也垂直”.
(4)利用面面垂直的性质.
3.判定线线垂直的方法
(1)平面几何中证明线线垂直的方法.
(2)线面垂直的性质:a⊥α,b?α?a⊥b.
(3)线面垂直的性质:a⊥α,b∥α?a⊥b.
4.判断面面垂直的方法
(1)利用定义:两个平面相交,所成的二面角是直二面角.
(2)判定定理:a?α,a⊥β?α⊥β.
三、空间角的求法
1.找异面直线所成角的三种方法
(1)利用图中已有的平行线平移.
(2)利用特殊点(线段的端点或中点)作平行线平移.
(3)补形平移.
2.线面角:求斜线与平面所成的角关键是找到斜线在平面内的射影,即确定过斜线上一点向平面所作垂线的垂足.通常是解由斜线段、垂线段、斜线在平面内的射影所组成的直角三角形.
返回
第二章 点、直线、平面之间的位置关系
1.整合知识结构,梳理各知识网络,进一步巩固、深化所学知识;
2.提高综合运用知识的能力和空间想象能力,在空间实现平行关系、垂直关系、垂直与平行关系之间的转化.
要点归纳
题型探究
达标检测
学习目标
要点归纳 主干梳理 点点落实
1.四个公理
公理1:如果一条直线上的______在一个平面内,那么这条直线上所有的点都在这个平面内.
公理2:过__________________的三点,有且只有一个平面.
公理3:如果两个不重合的平面有一个公共点,那么它们有且只有_____________________.
公理4:平行于同一条直线的两条直线互相_____.
2.直线与直线的位置关系
答案
————
共面直线
异面直线:不同在_____一个平面内,没有公共点
两点
不在同一条直线上
一条过该点的公共直线
平行
平行
相交
任何
3.平行的判定与性质
(1)直线与平面平行的判定与性质
答案
?
判定
性质
定义
定理
图形
条件
_________
___________________
______
____________________
结论
a∥α
b∥α
a∩α=?
a∥b
a∩α=?
a?α,b?α,
a∥b
a∥α
a∥α,a?β,
α∩β=b
(2)面面平行的判定与性质
答案
?
判定
性质
定义
定理
图形
条件
_________
_____________________
___________
_____,_________,_________
α∥β,a?β
结论
α∥β
α∥β
a∥b
a∥α
α∩β=?
a?β,b?β,
a∩b=P,
a∥α,b∥α
α∥β
β∩γ=b
α∩γ=a
(3)空间中的平行关系的内在联系
4.垂直的判定与性质
(1)直线与平面垂直
答案
?
图形
条件
结论
判定
a⊥b,b?α
(b为α内的______直线)
a⊥α
a⊥m,a⊥n,m、n?α,___________
a⊥α
任意
m∩n=O
答案
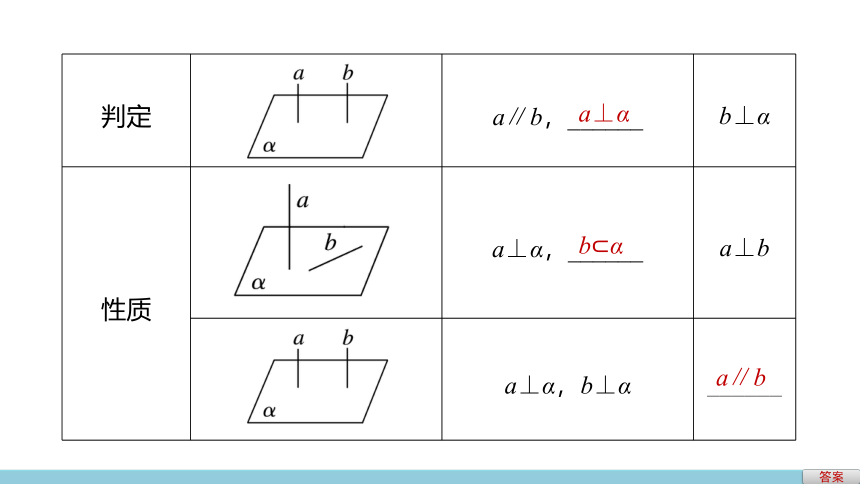
判定
a∥b,______
b⊥α
性质
a⊥α,______
a⊥b
a⊥α,b⊥α
______
a⊥α
b?α
a∥b
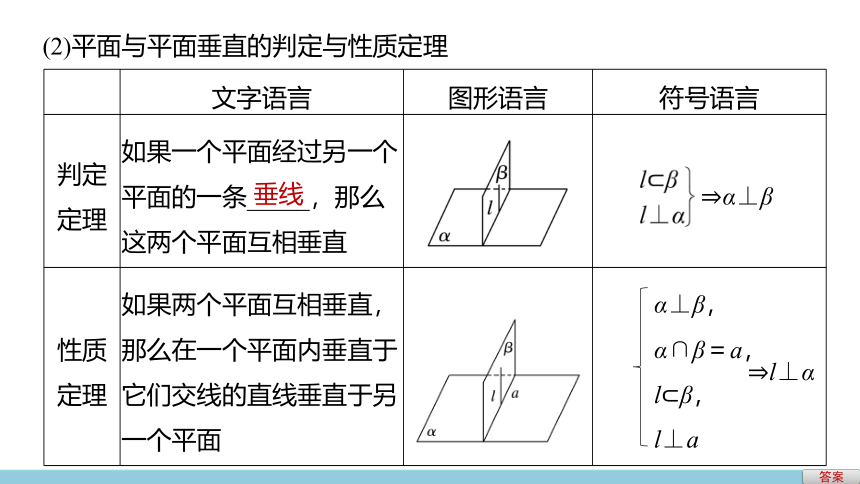
(2)平面与平面垂直的判定与性质定理
?
文字语言
图形语言
符号语言
判定定理
如果一个平面经过另一个平面的一条_____,那么这两个平面互相垂直
?α⊥β
性质定理
如果两个平面互相垂直,那么在一个平面内垂直于它们交线的直线垂直于另一个平面
?l⊥α
α⊥β,
α∩β=a,
l?β,
l⊥a
垂线
答案
(3)空间中的垂直关系的内在联系.
答案
5.空间角
(1)异面直线所成的角
①定义:设a,b是两条异面直线,经过空间任一点O作直线a′∥a,b′∥b,把a′与b′所成的_____________叫做异面直线a,b所成的角(或夹角).
②范围:设两异面直线所成角为θ,则0°<θ≤90°.
锐角(或直角)
(2)直线和平面所成的角
①平面的一条斜线与它在______________所成的锐角叫做这条直线与这个平面所成的角.
②当直线与平面垂直和平行(或直线在平面内)时,规定直线和平面所成的角分别为__________.
(3)二面角的有关概念
①二面角:从一条直线和由这条直线出发的_____________所组成的图形叫做二面角.
②二面角的平面角:以二面角的棱上任意一点为端点,在两个半平面内分别作_________的两条射线,这两条射线所成的角叫做二面角的平面角.
返回
答案
平面内的射影
90°和0°
两个半平面
垂直于棱
类型一 几何中共点、共线、共面问题
题型探究 重点难点 个个击破
例1 如图所示,空间四边形ABCD中,E,F分别为AB,AD的中点,G,H分别在BC,CD上,且BG∶GC=DH∶HC=1∶2.
求证:(1)E、F、G、H四点共面;
证明 ∵BG∶GC=DH∶HC,∴GH∥BD,
又EF∥BD,∴EF∥GH,
∴E、F、G、H四点共面.
解析答案
(2)GE与HF的交点在直线AC上.
证明 ∵G、H不是BC、CD的中点,∴EF≠GH.
又EF∥GH,∴EG与FH不平行,
则必相交,设交点为M.
反思与感悟
?M在面ABC与面ACD的交线上,
又面ABC∩面ACD=AC?M∈AC.
∴GE与HF的交点在直线AC上.
解析答案
反思与感悟
1.证明共面问题
证明共面问题,一般有两种证法:一是由某些元素确定一个平面,再证明其余元素在这个平面内;二是分别由不同元素确定若干个平面,再证明这些平面重合.
2.证明三点共线问题
证明空间三点共线问题,通常证明这些点都在两个面的交线上,即先确定出某两点在某两个平面的交线上,再证明第三个点是两个平面的公共点,当然必在两个平面的交线上.
3.证明三线共点问题
证明空间三线共点问题,先证两条直线交于一点,再证明第三条直线经过这点,把问题转化为证明点在直线上的问题.
跟踪训练1 如图,O是正方体ABCD-A1B1C1D1上底面ABCD的中心,M是正方体对角线AC1和截面A1BD的交点.求证:O、M、A1三点共线.
证明 ∵O∈AC,AC?平面ACC1A1,∴O∈平面ACC1A1.
∵M∈AC1,AC1?平面ACC1A1,∴M∈平面ACC1A1.
又已知A1∈平面ACC1A1,
即有O、M、A1三点都在平面ACC1A1上,
又O、M、A1三点都在平面A1BD上,
所以O、M、A1三点都在平面ACC1A1与平面A1BD的交线上,
所以O、M、A1三点共线.
解析答案
类型二 空间中的平行关系
例2 如图,E、F、G、H分别是正方体ABCD—A1B1C1D1的棱BC、CC1、C1D1、AA1的中点,
求证:(1)GE∥平面BB1D1D;
证明 如图,取B1D1中点O,连接GO,OB,
解析答案
∴OG綊BE,四边形BEGO为平行四边形.
∴OB∥GE.
∵OB?平面BDD1B1,GE?平面BDD1B1,
∴GE∥平面BDD1B1.
(2)平面BDF∥平面B1D1H.
证明 由正方体性质得B1D1∥BD,
∵B1D1?平面BDF,BD?平面BDF,
∴B1D1∥平面BDF.
连接HB,D1F,易证HBFD1是平行四边形,得HD1∥BF.
∵HD1?平面BDF,BF?平面BDF,
∴HD1∥平面BDF.
∵B1D1∩HD1=D1,
∴平面BDF∥平面B1D1H.
解析答案
反思与感悟
反思与感悟
1.判断线面平行的两种常用方法
面面平行判定的落脚点是线面平行,因此掌握线面平行的判定方法是必要的,判定线面平行的两种方法:
(1)利用线面平行的判定定理.
(2)利用面面平行的性质,即当两平面平行时,其中一平面内的任一直线平行于另一平面.
2.判断面面平行的常用方法
(1)利用面面平行的判定定理.
(2)面面平行的传递性(α∥β,β∥γ?α∥γ);
(3)利用线面垂直的性质(l⊥α,l⊥β?α∥β).
跟踪训练2 如图,△ABC为正三角形,EC⊥平面ABC,DB⊥平面ABC,CE=CA=2BD,M是EA的中点,N是EC的中点,求证:平面DMN∥平面ABC.
证明 ∵M、N分别是EA与EC的中点,∴MN∥AC,
又∵AC?平面ABC,MN?平面ABC,∴MN∥平面ABC,
∵DB⊥平面ABC,EC⊥平面ABC,∴BD∥EC,
∵N为EC中点,EC=2BD,∴NC綊BD,
∴四边形BCND为矩形,∴DN∥BC,
又∵DN?平面ABC,BC?平面ABC,
∴DN∥平面ABC,
又∵MN∩DN=N,∴平面DMN∥平面ABC.
解析答案
例3 如图所示,在四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,E是PC的中点.
证明:(1)CD⊥AE;
证明 在四棱锥P-ABCD中,
∵PA⊥底面ABCD,CD?平面ABCD,∴PA⊥CD.
∵AC⊥CD,PA∩AC=A,∴CD⊥平面PAC.
而AE?平面PAC,∴CD⊥AE.
类型三 空间中的垂直关系
解析答案
(2)PD⊥平面ABE.
证明 由PA=AB=BC,∠ABC=60°,可得AC=PA.
∵E是PC的中点,∴AE⊥PC.
由(1),知AE⊥CD,且PC∩CD=C,∴AE⊥平面PCD.
而PD?平面PCD,∴AE⊥PD.
∵PA⊥底面ABCD,∴PA⊥AB.
又∵AB⊥AD且PA∩AD=A,
∴AB⊥平面PAD,而PD?平面PAD,
∴AB⊥PD.
又∵AB∩AE=A,∴PD⊥平面ABE.
解析答案
反思与感悟
空间垂直关系的判定方法
(1)判定线线垂直的方法:
①计算所成的角为90°(包括平面角和异面直线所成的角);
②线面垂直的性质(若a⊥α,b?α,则a⊥b).
(2)判定线面垂直的方法:
①线面垂直定义(一般不易验证任意性);
②线面垂直的判定定理(a⊥b,a⊥c,b?α,c?α,b∩c=M?a⊥α);
③平行线垂直平面的传递性质(a∥b,b⊥α?a⊥α);
④面面垂直的性质(α⊥β,α∩β=l,a?β,a⊥l?a⊥α);
⑤面面平行的性质(a⊥α,α∥β?a⊥β);
⑥面面垂直的性质(α∩β=l,α⊥γ,β⊥γ?l⊥γ).
反思与感悟
反思与感悟
(3)面面垂直的判定方法:
①根据定义(作两平面构成二面角的平面角,计算其为90°);
②面面垂直的判定定理(a⊥β,a?α?α⊥β).
跟踪训练3 如图,A,B,C,D为空间四点.在△ABC中,AB=2,
(1)当平面ADB⊥平面ABC时,求CD;
解 如图,取AB的中点E,连接DE,CE,
因为△ADB是等边三角形,所以DE⊥AB.
当平面ADB⊥平面ABC时,因为平面ADB∩平面ABC=AB,
所以DE⊥平面ABC,可知DE⊥CE,
解析答案
解 当△ADB以AB为轴转动时,总有AB⊥CD.
证明如下:①当D在平面ABC内时,
因为AC=BC,AD=BD,
所以C,D都在线段AB的垂直平分线上,即AB⊥CD.
②当D不在平面ABC内时,
由(1)知AB⊥DE.又因AC=BC,所以AB⊥CE.
又DE,CE为相交直线,所以AB⊥平面CDE,
由CD?平面CDE,得AB⊥CD.
综上所述,总有AB⊥CD.
解析答案
(2)当△ADB转动时,是否总有AB⊥CD?证明你的结论.
类型四 空间角问题
解析答案
例4 如图,在四棱锥P—ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,E是PC的中点.
(1)求PB和平面PAD所成的角的大小;
解 在四棱锥P—ABCD中,
因为PA⊥底面ABCD,AB?平面ABCD,
故PA⊥AB.又AB⊥AD,PA∩AD=A,
从而AB⊥平面PAD,故PB在平面PAD内的射影为PA,
从而∠APB为PB和平面PAD所成的角.
在Rt△PAB中,AB=PA,故∠APB=45°.
所以PB和平面PAD所成的角的大小为45°.
(2)证明:AE⊥平面PCD;
证明 在四棱锥P—ABCD中,
因为PA⊥底面ABCD,CD?平面ABCD,
故CD⊥PA.由条件CD⊥AC,PA∩AC=A,
所以CD⊥平面PAC.
又AE?平面PAC,所以AE⊥CD.
由PA=AB=BC,∠ABC=60°,可得AC=PA.
因为E是PC的中点,所以AE⊥PC.
又PC∩CD=C,所以AE⊥平面PCD.
解析答案
(3)求二面角A—PD—C的正弦值.
解析答案
反思与感悟
解 过点E作EM⊥PD,垂足为M,连接AM,如图所示.
由(2)知,AE⊥平面PCD,AM在平面PCD内的射影是EM,
则可证得AM⊥PD.
因此∠AME是二面角A—PD—C的平面角.
由已知,可得∠CAD=30°.
设AC=a,可得
在Rt△ADP中,∵AM⊥PD,∴AM·PD=PA·AD,
反思与感悟
1.求异面直线所成的角常用平移转化法(转化为相交直线的夹角).
2.求直线与平面所成的角常用射影转化法(即作垂线、找射影).
3.二面角的平面角的作法常有三种:(1)定义法;(2)垂线法;(3)垂面法.
反思与感悟
解析答案
跟踪训练4 如图,正方体的棱长为1,B′C∩BC′=O,求:
(1)AO与A′C′所成角的度数;
解 ∵A′C′∥AC,
∴AO与A′C′所成的角就是∠OAC.
∵AB⊥平面BC′,OC?平面BC′,
∴OC⊥AB,又OC⊥BO,AB∩BO=B.
∴OC⊥平面ABO.
又OA?平面ABO,∴OC⊥OA.
解析答案
(2)AO与平面ABCD所成角的正切值;
解 如图,作OE⊥BC于E,连接AE.
∵平面BC′⊥平面ABCD,
∴OE⊥平面ABCD,
∴∠OAE为OA与平面ABCD所成的角.
解析答案
(3)平面AOB与平面AOC所成角的度数.
解 ∵OC⊥OA,OC⊥OB,OA∩OB=O,
∴OC⊥平面AOB.
又∵OC?平面AOC,
∴平面AOB⊥平面AOC.
即平面AOB与平面AOC所成角的度数为90°.
返回
1
2
3
达标检测
解析答案
1.下列四个结论:
(1)两条直线都和同一个平面平行,则这两条直线平行.
(2)两条直线没有公共点,则这两条直线平行.
(3)两条直线都和第三条直线垂直,则这两条直线平行.
(4)一条直线和一个平面内无数条直线没有公共点,则这条直线和这个平面平行.
其中正确的个数为( )
A.0 B.1 C.2 D.3
4
解析 (1)两条直线都和同一个平面平行,这两条直线三种位置关系都有可能;
(2)两条直线没有公共点,则这两条直线平行或异面;
(3)两条直线都和第三条直线垂直,则这两条直线三种位置关系都有可能;
(4)一条直线和一个平面内无数条直线没有公共点,则这条直线也可在这个平面内.
答案 A
1
2
3
4
解析答案
2.设有不同的直线m、n和不同的平面α、β,下列四个命题中,正确的是( )
A.若m∥α,n∥α,则m∥n
B.若m?α,n?α,m∥β,n∥β,则α∥β
C.若α⊥β,m?α,则m⊥β
D.若α⊥β,m⊥β,m?α,则m∥α
1
2
3
4
解析 选项A中当m∥α,n∥α时,m与n可以平行、相交、异面;
选项B中满足条件的α与β可以平行,也可以相交;
选项C中,当α⊥β,m?α时,m与β可以垂直,也可以平行等.
故选项A、B、C均不正确.
D
解析答案
3.如图,已知正方体ABCD-A1B1C1D1,O是底面ABCD对角线的交点.
求证:(1)C1O∥面AB1D1;
证明 如图,连接A1C1,设A1C1∩B1D1=O1,连接AO1,
∵ABCD-A1B1C1D1是正方体,∴A1ACC1是平行四边形,
∴A1C1∥AC且A1C1=AC,
又O1,O分别是A1C1,AC的中点,
∴O1C1∥AO且O1C1=AO,
∴四边形AOC1O1是平行四边形,
∴C1O∥AO1,AO1?面AB1D1,C1O?面AB1D1,
∴C1O∥面AB1D1.
1
2
3
4
解析答案
(2)A1C⊥面AB1D1.
证明 ∵CC1⊥面A1B1C1D1,
∴CC1⊥B1D1,
又∵A1C1⊥B1D1,
∴B1D1⊥面A1C1CA,
即A1C⊥B1D1,同理可证A1C⊥AB1,
又B1D1∩AB1=B1,∴A1C⊥面AB1D1.
1
2
3
4
解析答案
1
2
3
4
4.如图,AB是⊙O的直径,PA垂直于⊙O所在的平面,C是圆周上不同于A,B的一动点.
(1)证明:△PBC是直角三角形.
解 因为AB是⊙O的直径,C是圆周上不同于A,
B的一动点,
所以BC⊥AC,
因为PA⊥平面ABC,所以BC⊥PA,
又PA∩AC=A,所以BC⊥平面PAC,
所以BC⊥PC,
所以△PBC是直角三角形.
1
2
3
4
(2)若PA=AB=2,且当直线PC与平面ABC所成角正切值为 时,求直线AB与平面PBC所成角的正弦值.
解析答案
1
2
3
4
解 如图,过A作AH⊥PC于H,连接BH,
因为BC⊥平面PAC,所以BC⊥AH,PC∩BC=C,
所以AH⊥平面PBC,所以∠ABH是直线AB与平面PBC所成角,
因为PA⊥平面ABC,所以∠PCA即是PC与平面ABC所成角,
规律与方法
一、平行关系
1.平行问题的转化关系
2.直线与平面平行的主要判定方法
(1)定义法;(2)判定定理;(3)面与面平行的性质.
3.平面与平面平行的主要判定方法
(1)定义法;(2)判定定理;(3)推论;
(4)a⊥α,a⊥β?α∥β.
二、垂直关系
1.空间中垂直关系的相互转化
2.判定线面垂直的常用方法
(1)利用线面垂直的判定定理.
(2)利用“两平行线中的一条与平面垂直,则另一条也与这个平面垂直”.
(3)利用“一条直线垂直于两平行平面中的一个,则与另一个也垂直”.
(4)利用面面垂直的性质.
3.判定线线垂直的方法
(1)平面几何中证明线线垂直的方法.
(2)线面垂直的性质:a⊥α,b?α?a⊥b.
(3)线面垂直的性质:a⊥α,b∥α?a⊥b.
4.判断面面垂直的方法
(1)利用定义:两个平面相交,所成的二面角是直二面角.
(2)判定定理:a?α,a⊥β?α⊥β.
三、空间角的求法
1.找异面直线所成角的三种方法
(1)利用图中已有的平行线平移.
(2)利用特殊点(线段的端点或中点)作平行线平移.
(3)补形平移.
2.线面角:求斜线与平面所成的角关键是找到斜线在平面内的射影,即确定过斜线上一点向平面所作垂线的垂足.通常是解由斜线段、垂线段、斜线在平面内的射影所组成的直角三角形.
返回
