高一数学人教版A版必修二课件:第三章 直线与方程章末复习课 课件(共33张PPT)
文档属性
| 名称 | 高一数学人教版A版必修二课件:第三章 直线与方程章末复习课 课件(共33张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-24 18:21:28 | ||
图片预览











文档简介
章末复习课
第三章 直线与方程
1.整合知识结构,梳理知识网络,进一步巩固、深化所学知识;
2.培养综合运用知识解决问题的能力,能灵活选择直线方程的形式并熟练运用待定系数法求解,渗透数形结合、分类讨论的数学思想.
要点归纳
题型探究
达标检测
学习目标
要点归纳 主干梳理 点点落实
1.直线的倾斜角与斜率
(1)直线的倾斜角α的范围是 .
(3)斜率的求法:
①依据倾斜角;②依据直线方程;③依据两点的坐标.
答案
存在
0°≤α<180°
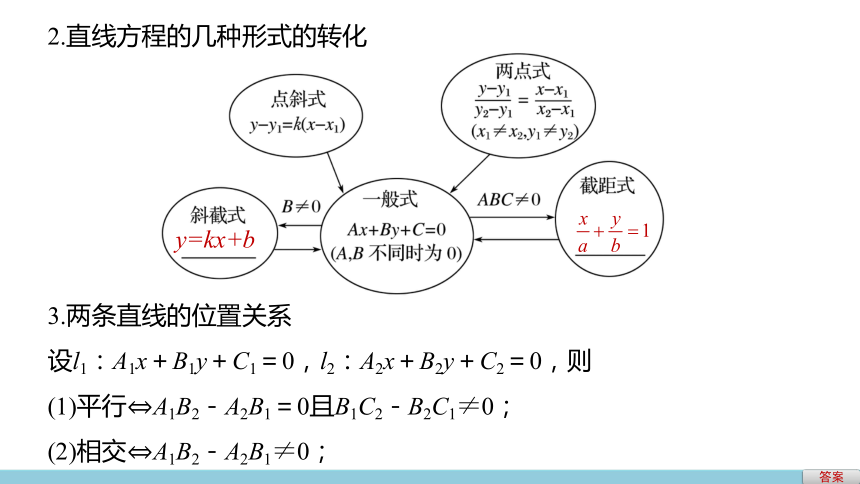
2.直线方程的几种形式的转化
3.两条直线的位置关系
设l1:A1x+B1y+C1=0,l2:A2x+B2y+C2=0,则
(1)平行?A1B2-A2B1=0且B1C2-B2C1≠0;
(2)相交?A1B2-A2B1≠0;
y=kx+b
答案
返回
答案
类型一 待定系数法的应用
题型探究 重点难点 个个击破
例1 直线l被两条直线l1:4x+y+3=0和l2:3x-5y-5=0截得的线段的中点为P(-1,2),求直线l的方程.
解析答案
反思与感悟
解 方法一 设直线l与l1的交点为A(x0,y0),
由已知条件,得直线l与l2的交点为B(-2-x0 ,4-y0),
即3x+y+1=0.
解析答案
反思与感悟
方法二 设直线l的方程为y-2=k(x+1),即kx-y+k+2=0.
因此所求直线方程为y-2=-3(x+1),
即3x+y+1=0.
解得k=-3.
解析答案
反思与感悟
方法三 两直线l1和l2的方程为
(4x+y+3)(3x-5y-5)=0, ①
将上述方程中(x,y)换成(-2-x,4-y),
整理可得l1与l2关于(-1,2)对称图形的方程:
(4x+y+1)(3x-5y+31)=0. ②
①-②整理得3x+y+1=0,即为所求直线方程.
反思与感悟
反思与感悟
待定系数法,就是所研究的式子(方程)的结构是确定的,但它的全部或部分系数是待定的,然后根据题中条件来确定这些系数的方法.直线的方程常用待定系数法求解.选择合适的直线方程的形式是很重要的,一般情况下,与截距有关的,可设直线的斜截式方程或截距式方程;与斜率有关的,可设直线的斜截式或点斜式方程等.
跟踪训练1 求在两坐标轴上截距相等,且到点A(3,1)的距离为 的直线的方程.
解析答案
解 当直线过原点时,设直线的方程为y=kx,即kx-y=0.
所以所求直线的方程为x-y=0或x+7y=0.
当直线不经过原点时,
解得a=2或a=6.
所以所求直线的方程为x+y-2=0或x+y-6=0.
综上可知,所求直线的方程为x-y=0或x+7y=0或x+y-2=0
或x+y-6=0.
类型二 数形结合思想的应用
解析答案
反思与感悟
解析答案
解 将已知条件变形为
故设M(x,0),A(1,2),B(2,1),
∴原函数变为y=||MA|-|MB||.
则上式的几何意义为:x轴上的点M(x,0)到定点A(1,2)与B(2,1)的距离的差的绝对值,由图可知,当|AM|=|BM|时,y取最小值0.
此时点M在坐标原点, y最小=0.
解得x=0,
反思与感悟
又由三角形性质可知||MA|-|MB||≤|AB|,即当||MA|-|MB||=|AB|,
也即当A、B、M三点共线时,y取最大值.
由已知得AB的方程为y-2=-(x-1),即y=-x+3,
令y=0得x=3,
∴当x=3时,
反思与感悟
数形结合是解析几何的灵魂,两点间的距离公式和点到直线的距离公式是数形结合常见的结合点,常用这两个公式把抽象的代数问题转化为几何问题来解决,也能把几何问题转化为代数问题来解决,这就是数形结合.
跟踪训练2 已知实数x、y满足4x+3y-10=0,求x2+y2的最小值.
解析答案
解 设点P(x,y),则点P在直线l:4x+3y-10=0上,
如图所示,当OP⊥l时,|OP|取最小值|OM|,
即|OP|的最小值是2.
所以x2+y2的最小值是4.
类型三 分类讨论思想的应用
解析答案
反思与感悟
例3 过点P(-1,0)、Q(0,2)分别作两条互相平行的直线,使它们在x轴上截距之差的绝对值为1,求这两条直线的方程.
反思与感悟
解 当两条直线的斜率不存在时,两条直线的方程分别为x=-1,x=0,它们在x轴上截距之差的绝对值为1,符合题意.
当直线的斜率存在时,设其斜率为k,
则两条直线的方程分别为y=k(x+1),y-2=kx.
令y=0,得x=-1与x=
由题意得 即k=1.
∴两条直线的方程分别为y=x+1,y=x+2,
即为x-y+1=0,x-y+2=0.
综上可知,所求的两直线方程分别为x=-1,x=0或x-y+1=0,
x-y+2=0.
反思与感悟
本章涉及直线方程的形式时,常遇到斜率的存在性问题的讨论,如两直线平行(或垂直)时,斜率是否存在;已知直线过定点时,选择点斜式方程,要考虑斜率是否存在.
解析答案
跟踪训练3 已知经过点A(-2,0)和点B(1,3a)的直线l1与经过点P(0,-1)和点Q(a,-2a)的直线l2互相垂直,求实数a的值.
当a=0时,P(0,-1),Q(0,0),这时直线l2为y轴,
A(-2,0)、B(1,0),这时直线l1为x轴,显然l1⊥l2.
综上可知,实数a的值为1或0.
类型四 对称问题的求法
解析答案
例4 已知直线l:y=3x+3,试求:
(1)点P(4,5)关于直线l的对称点的坐标;
解 设点P关于直线l的对称点为P′(x′,y′),
则PP′的中点M在直线l上,且直线PP′垂直于直线l.
∴P′点的坐标为(-2,7).
解析答案
反思与感悟
(2)直线l关于点A(3,2)对称的直线方程.
解 设直线l关于点A(3,2)对称的直线为l3,则直线l上任一点P(x1,y1)关于点A的对称点P3(x3,y3)一定在直线l3上,反之也成立.
代入l的方程后,得3x3-y3-17=0.
即l3的方程为3x-y-17=0.
反思与感悟
(1)中心对称
①两点关于点对称:设P1(x1,y1),P(a,b),则P1(x1,y1)关于P(a,b)对称的点为P2(2a-x1 ,2b-y1),即P为线段P1P2的中点.
②两直线关于点对称:设直线l1,l2关于点P对称,这时其中一条直线上任一点关于点P对称的点在另外一条直线上,必有l1∥l2,且P到l1、l2的距离相等.
(2)轴对称
两点关于直线对称:设P1,P2关于直线l对称,则直线P1P2与l垂直,且P1P2的中点在l上.
解析答案
跟踪训练4 在直线l:3x-y-1=0上求一点P,使得:
(1)P到A(4,1)和B(0,4)的距离之差最大;
解 如图,B关于l的对称点B′(3,3).
直线AB′的方程为2x+y-9=0,
即P(2,5).
解析答案
(2)P到A(4,1)和C(3,4)的距离之和最小.
由图象可知:|PA|+|PC|≥|AC′|.
返回
1
2
3
达标检测
解析答案
1.直线l在两坐标轴上的截距相等,且点M(1,-1)到直线l的距离为 ,则直线l的方程为_______________.
4
5
解析 当直线l经过原点时,设直线方程为y=kx,
∴直线方程为x-y=0,
当在坐标轴上的截距不为零时,
解得k=1,
即x+y-a=0,
得a=±2,
∴直线方程为x+y-2=0或x+y+2=0.
综上所述得l的方程为x-y=0或x+y+2=0或x+y-2=0.
答案 x-y=0或x+y+2=0或x+y-2=0
1
2
3
4
解析答案
2.已知直线l经过2x+y-5=0与x-2y=0的交点,则点A(5,0)到l的距离的最大值为________.
1
2
3
4
∴直线l过点(2,1).
由题意得,当l与点A和交点连线垂直时,点A到l的距离为最大,
解析答案
3.已知A(2,4)与B(3,3)关于直线l对称,则直线l的方程为___________.
解析 由题意知,直线l即为AB的垂直平分线,
∴kl·kAB=-1,得kl=1,
1
2
3
4
x-y+1=0
即x-y+1=0.
解析答案
1
2
3
4
4.设直线l的方程为(a+1)x+y+2-a=0 (a∈R).
(1)若l在两坐标轴上截距相等,求l的方程;
解 当直线过原点时,该直线在x轴和y轴上的截距为零,
∴a=2,方程即为3x+y=0.
当直线不经过原点时,截距存在且均不为0.
∴a=0,方程即为x+y+2=0.
综上,l的方程为3x+y=0或x+y+2=0.
1
2
3
4
(2)若l不经过第二象限,求实数a的取值范围.
解 将l的方程化为y=-(a+1)x+a-2,
∴a≤-1.
综上可知a的取值范围是a≤-1.
解析答案
规律与方法
1.一般地,与直线Ax+By+C=0平行的直线方程可设为Ax+By+m=0;与之垂直的直线方程可设为Bx-Ay+n=0.
2.过直线l1:A1x+B1y+C1=0与l2:A2x+B2y+C2=0的交点的直线系方程为A1x+B1y+C1+λ(A2x+B2y+C2)=0 (λ∈R),但不包括l2.
3.点到直线与两平行线间的距离的使用条件:
(1)求点到直线的距离时,应先化直线方程为一般式.
(2)求两平行线之间的距离时,应先将方程化为一般式且x,y的系数对应相等.
返回
第三章 直线与方程
1.整合知识结构,梳理知识网络,进一步巩固、深化所学知识;
2.培养综合运用知识解决问题的能力,能灵活选择直线方程的形式并熟练运用待定系数法求解,渗透数形结合、分类讨论的数学思想.
要点归纳
题型探究
达标检测
学习目标
要点归纳 主干梳理 点点落实
1.直线的倾斜角与斜率
(1)直线的倾斜角α的范围是 .
(3)斜率的求法:
①依据倾斜角;②依据直线方程;③依据两点的坐标.
答案
存在
0°≤α<180°
2.直线方程的几种形式的转化
3.两条直线的位置关系
设l1:A1x+B1y+C1=0,l2:A2x+B2y+C2=0,则
(1)平行?A1B2-A2B1=0且B1C2-B2C1≠0;
(2)相交?A1B2-A2B1≠0;
y=kx+b
答案
返回
答案
类型一 待定系数法的应用
题型探究 重点难点 个个击破
例1 直线l被两条直线l1:4x+y+3=0和l2:3x-5y-5=0截得的线段的中点为P(-1,2),求直线l的方程.
解析答案
反思与感悟
解 方法一 设直线l与l1的交点为A(x0,y0),
由已知条件,得直线l与l2的交点为B(-2-x0 ,4-y0),
即3x+y+1=0.
解析答案
反思与感悟
方法二 设直线l的方程为y-2=k(x+1),即kx-y+k+2=0.
因此所求直线方程为y-2=-3(x+1),
即3x+y+1=0.
解得k=-3.
解析答案
反思与感悟
方法三 两直线l1和l2的方程为
(4x+y+3)(3x-5y-5)=0, ①
将上述方程中(x,y)换成(-2-x,4-y),
整理可得l1与l2关于(-1,2)对称图形的方程:
(4x+y+1)(3x-5y+31)=0. ②
①-②整理得3x+y+1=0,即为所求直线方程.
反思与感悟
反思与感悟
待定系数法,就是所研究的式子(方程)的结构是确定的,但它的全部或部分系数是待定的,然后根据题中条件来确定这些系数的方法.直线的方程常用待定系数法求解.选择合适的直线方程的形式是很重要的,一般情况下,与截距有关的,可设直线的斜截式方程或截距式方程;与斜率有关的,可设直线的斜截式或点斜式方程等.
跟踪训练1 求在两坐标轴上截距相等,且到点A(3,1)的距离为 的直线的方程.
解析答案
解 当直线过原点时,设直线的方程为y=kx,即kx-y=0.
所以所求直线的方程为x-y=0或x+7y=0.
当直线不经过原点时,
解得a=2或a=6.
所以所求直线的方程为x+y-2=0或x+y-6=0.
综上可知,所求直线的方程为x-y=0或x+7y=0或x+y-2=0
或x+y-6=0.
类型二 数形结合思想的应用
解析答案
反思与感悟
解析答案
解 将已知条件变形为
故设M(x,0),A(1,2),B(2,1),
∴原函数变为y=||MA|-|MB||.
则上式的几何意义为:x轴上的点M(x,0)到定点A(1,2)与B(2,1)的距离的差的绝对值,由图可知,当|AM|=|BM|时,y取最小值0.
此时点M在坐标原点, y最小=0.
解得x=0,
反思与感悟
又由三角形性质可知||MA|-|MB||≤|AB|,即当||MA|-|MB||=|AB|,
也即当A、B、M三点共线时,y取最大值.
由已知得AB的方程为y-2=-(x-1),即y=-x+3,
令y=0得x=3,
∴当x=3时,
反思与感悟
数形结合是解析几何的灵魂,两点间的距离公式和点到直线的距离公式是数形结合常见的结合点,常用这两个公式把抽象的代数问题转化为几何问题来解决,也能把几何问题转化为代数问题来解决,这就是数形结合.
跟踪训练2 已知实数x、y满足4x+3y-10=0,求x2+y2的最小值.
解析答案
解 设点P(x,y),则点P在直线l:4x+3y-10=0上,
如图所示,当OP⊥l时,|OP|取最小值|OM|,
即|OP|的最小值是2.
所以x2+y2的最小值是4.
类型三 分类讨论思想的应用
解析答案
反思与感悟
例3 过点P(-1,0)、Q(0,2)分别作两条互相平行的直线,使它们在x轴上截距之差的绝对值为1,求这两条直线的方程.
反思与感悟
解 当两条直线的斜率不存在时,两条直线的方程分别为x=-1,x=0,它们在x轴上截距之差的绝对值为1,符合题意.
当直线的斜率存在时,设其斜率为k,
则两条直线的方程分别为y=k(x+1),y-2=kx.
令y=0,得x=-1与x=
由题意得 即k=1.
∴两条直线的方程分别为y=x+1,y=x+2,
即为x-y+1=0,x-y+2=0.
综上可知,所求的两直线方程分别为x=-1,x=0或x-y+1=0,
x-y+2=0.
反思与感悟
本章涉及直线方程的形式时,常遇到斜率的存在性问题的讨论,如两直线平行(或垂直)时,斜率是否存在;已知直线过定点时,选择点斜式方程,要考虑斜率是否存在.
解析答案
跟踪训练3 已知经过点A(-2,0)和点B(1,3a)的直线l1与经过点P(0,-1)和点Q(a,-2a)的直线l2互相垂直,求实数a的值.
当a=0时,P(0,-1),Q(0,0),这时直线l2为y轴,
A(-2,0)、B(1,0),这时直线l1为x轴,显然l1⊥l2.
综上可知,实数a的值为1或0.
类型四 对称问题的求法
解析答案
例4 已知直线l:y=3x+3,试求:
(1)点P(4,5)关于直线l的对称点的坐标;
解 设点P关于直线l的对称点为P′(x′,y′),
则PP′的中点M在直线l上,且直线PP′垂直于直线l.
∴P′点的坐标为(-2,7).
解析答案
反思与感悟
(2)直线l关于点A(3,2)对称的直线方程.
解 设直线l关于点A(3,2)对称的直线为l3,则直线l上任一点P(x1,y1)关于点A的对称点P3(x3,y3)一定在直线l3上,反之也成立.
代入l的方程后,得3x3-y3-17=0.
即l3的方程为3x-y-17=0.
反思与感悟
(1)中心对称
①两点关于点对称:设P1(x1,y1),P(a,b),则P1(x1,y1)关于P(a,b)对称的点为P2(2a-x1 ,2b-y1),即P为线段P1P2的中点.
②两直线关于点对称:设直线l1,l2关于点P对称,这时其中一条直线上任一点关于点P对称的点在另外一条直线上,必有l1∥l2,且P到l1、l2的距离相等.
(2)轴对称
两点关于直线对称:设P1,P2关于直线l对称,则直线P1P2与l垂直,且P1P2的中点在l上.
解析答案
跟踪训练4 在直线l:3x-y-1=0上求一点P,使得:
(1)P到A(4,1)和B(0,4)的距离之差最大;
解 如图,B关于l的对称点B′(3,3).
直线AB′的方程为2x+y-9=0,
即P(2,5).
解析答案
(2)P到A(4,1)和C(3,4)的距离之和最小.
由图象可知:|PA|+|PC|≥|AC′|.
返回
1
2
3
达标检测
解析答案
1.直线l在两坐标轴上的截距相等,且点M(1,-1)到直线l的距离为 ,则直线l的方程为_______________.
4
5
解析 当直线l经过原点时,设直线方程为y=kx,
∴直线方程为x-y=0,
当在坐标轴上的截距不为零时,
解得k=1,
即x+y-a=0,
得a=±2,
∴直线方程为x+y-2=0或x+y+2=0.
综上所述得l的方程为x-y=0或x+y+2=0或x+y-2=0.
答案 x-y=0或x+y+2=0或x+y-2=0
1
2
3
4
解析答案
2.已知直线l经过2x+y-5=0与x-2y=0的交点,则点A(5,0)到l的距离的最大值为________.
1
2
3
4
∴直线l过点(2,1).
由题意得,当l与点A和交点连线垂直时,点A到l的距离为最大,
解析答案
3.已知A(2,4)与B(3,3)关于直线l对称,则直线l的方程为___________.
解析 由题意知,直线l即为AB的垂直平分线,
∴kl·kAB=-1,得kl=1,
1
2
3
4
x-y+1=0
即x-y+1=0.
解析答案
1
2
3
4
4.设直线l的方程为(a+1)x+y+2-a=0 (a∈R).
(1)若l在两坐标轴上截距相等,求l的方程;
解 当直线过原点时,该直线在x轴和y轴上的截距为零,
∴a=2,方程即为3x+y=0.
当直线不经过原点时,截距存在且均不为0.
∴a=0,方程即为x+y+2=0.
综上,l的方程为3x+y=0或x+y+2=0.
1
2
3
4
(2)若l不经过第二象限,求实数a的取值范围.
解 将l的方程化为y=-(a+1)x+a-2,
∴a≤-1.
综上可知a的取值范围是a≤-1.
解析答案
规律与方法
1.一般地,与直线Ax+By+C=0平行的直线方程可设为Ax+By+m=0;与之垂直的直线方程可设为Bx-Ay+n=0.
2.过直线l1:A1x+B1y+C1=0与l2:A2x+B2y+C2=0的交点的直线系方程为A1x+B1y+C1+λ(A2x+B2y+C2)=0 (λ∈R),但不包括l2.
3.点到直线与两平行线间的距离的使用条件:
(1)求点到直线的距离时,应先化直线方程为一般式.
(2)求两平行线之间的距离时,应先将方程化为一般式且x,y的系数对应相等.
返回
