五年级下册数学试题-总复习二:图形与几何、统计 人教版(含解析)
文档属性
| 名称 | 五年级下册数学试题-总复习二:图形与几何、统计 人教版(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 992.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-23 07:34:15 | ||
图片预览

文档简介
人教版数学2019-2020学年五年级下册总复习二:图形与几何、统计
一、填空题(共22分)
1.钟面上,指针从12:05到12:20,分针按________时针旋转了________度。
2.做一个长6分米,宽5分米,高3分米的无盖鱼缸,用角钢做它的框架,至少需要角钢________分米,至少需要玻璃________平方分米,最多可装水________立方分米。
3.如图,把一张边长9厘米的正方形纸,剪成一个“十字形”图案,折成了一个最大的无盖正方体纸盒。这个正方体纸盒用了________平方厘米的纸,体积是________立方厘米。
4.用一根长1米的铁丝焊接成一个长方体框架,它的底面周长是30厘米,高是________厘米。
5.一个长方体的底面积为20平方厘米,前面面积为15平方厘米,且相交于一个顶点的三条棱彼此互质,这个长方体的体积是________立方厘米。
6.一个长方体容器的底面积是80cm2 , 浸没着大,小两个球时,水面正好到容器口。现在先后取出这两个球,水面变化情况如下图所示。小球的体积是________?cm3 , 大球的体积是________?cm3。小球的体积是大球的________。
7.?
(1)从正面看到的图形是 的有________;
(2)从左面看到的图形是 的有________;
(3)从上面看到的图形是 的有________。
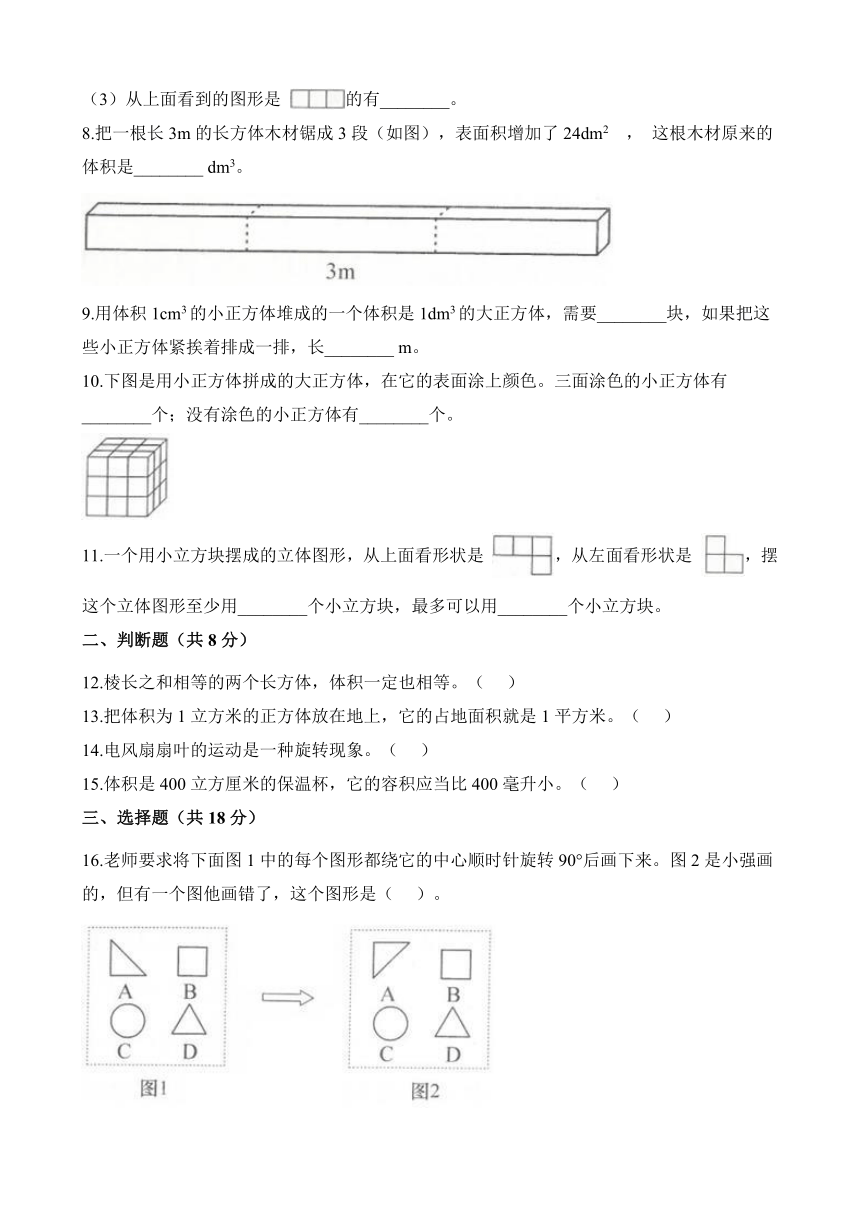
8.把一根长3m的长方体木材锯成3段(如图),表面积增加了24dm2 , 这根木材原来的体积是________?dm3。
9.用体积1cm3的小正方体堆成的一个体积是1dm3的大正方体,需要________块,如果把这些小正方体紧挨着排成一排,长________?m。
10.下图是用小正方体拼成的大正方体,在它的表面涂上颜色。三面涂色的小正方体有________个;没有涂色的小正方体有________个。
11.一个用小立方块摆成的立体图形,从上面看形状是 ,从左面看形状是 ,摆这个立体图形至少用________个小立方块,最多可以用________个小立方块。
二、判断题(共8分)
12.棱长之和相等的两个长方体,体积一定也相等。(??? )
13.把体积为1立方米的正方体放在地上,它的占地面积就是1平方米。(??? )
14.电风扇扇叶的运动是一种旋转现象。(??? )
15.体积是400立方厘米的保温杯,它的容积应当比400毫升小。(??? )
三、选择题(共18分)
16.老师要求将下面图1中的每个图形都绕它的中心顺时针旋转90°后画下来。图2是小强画的,但有一个图他画错了,这个图形是(??? )。
A.?A???????????????????????????????????????????B.?B?????????????????????????????????C.?C???????????????????????????????????????????D.?D
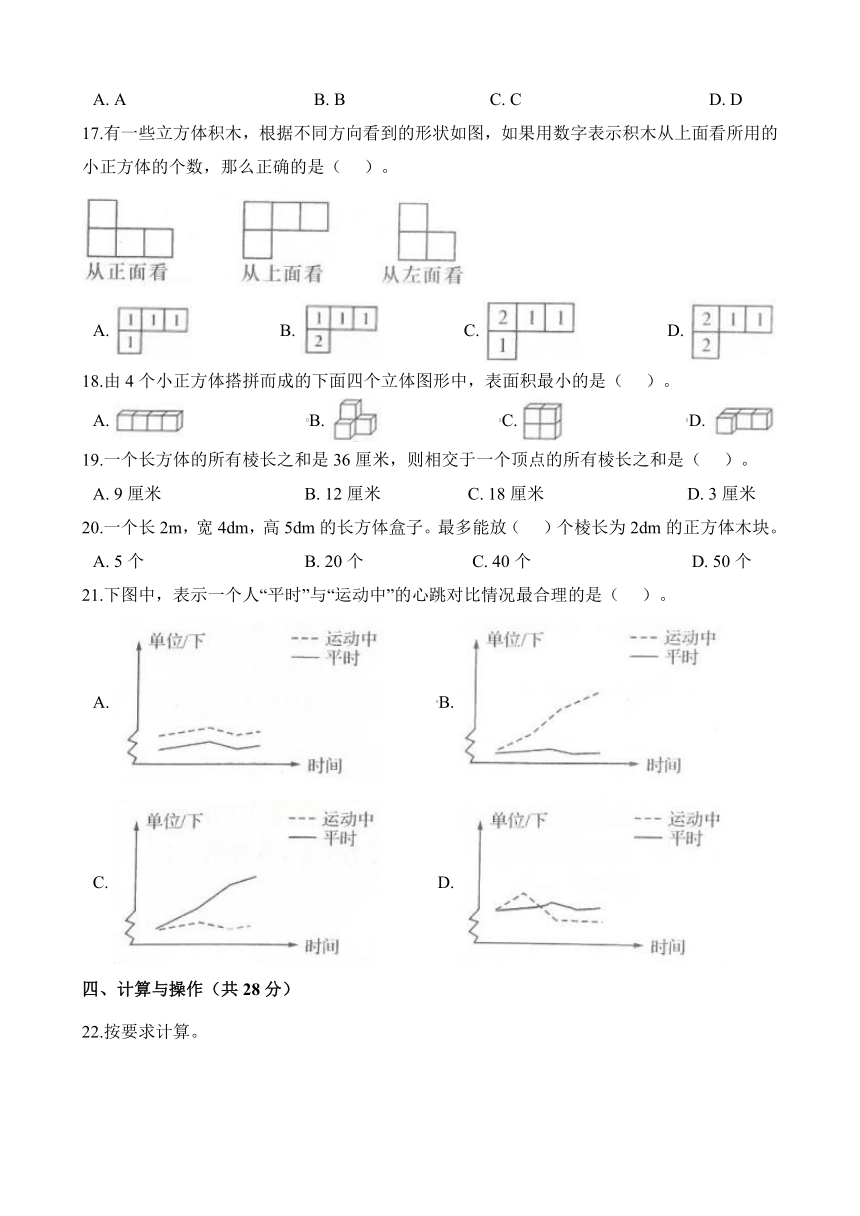
17.有一些立方体积木,根据不同方向看到的形状如图,如果用数字表示积木从上面看所用的小正方体的个数,那么正确的是(??? )。
A.?????????????????????B.????????????????????C.?????????????????????D.?
18.由4个小正方体搭拼而成的下面四个立体图形中,表面积最小的是(??? )。
A.?????????????????????????????B.????????????????????????????C.?????????????????????????????D.?
19.一个长方体的所有棱长之和是36厘米,则相交于一个顶点的所有棱长之和是(??? )。
A.?9厘米?????????????????????????????????B.?12厘米????????????????????C.?18厘米?????????????????????????????????D.?3厘米
20.一个长2m,宽4dm,高5dm的长方体盒子。最多能放(??? )个棱长为2dm的正方体木块。
A.?5个?????????????????????????????????????B.?20个?????????????????????????C.?40个?????????????????????????????????????D.?50个
21.下图中,表示一个人“平时”与“运动中”的心跳对比情况最合理的是(??? )。
A.?????????????B.?
C.??????????????D.?
四、计算与操作(共28分)
22.按要求计算。
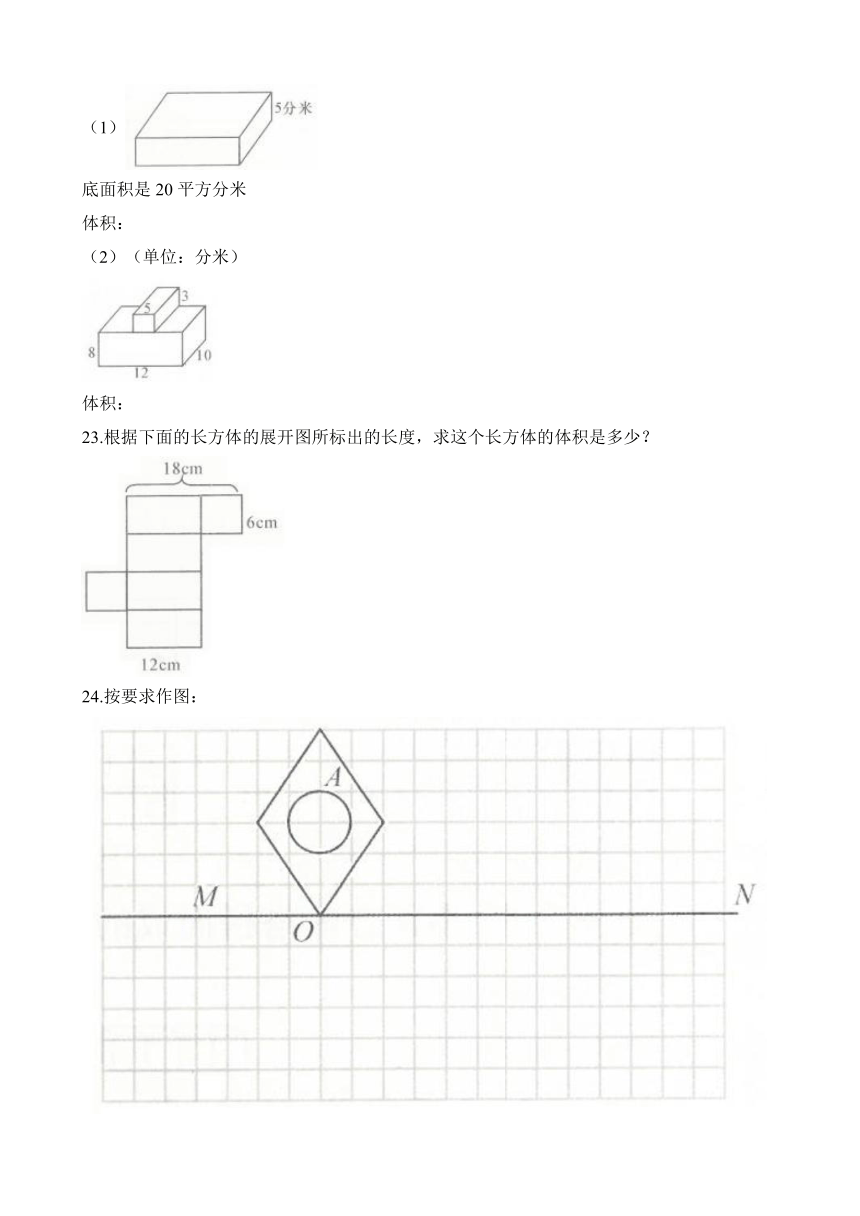
(1)
底面积是20平方分米
体积:
(2)(单位:分米)
体积:
23.根据下面的长方体的展开图所标出的长度,求这个长方体的体积是多少?
24.按要求作图:
(1)以直线MN为对称轴作图A的轴对称图形,得到图形B;
(2)将图形B绕点O逆时针旋转90度,得到图形C;
(3)将图形C向右平移6格,得到图形D。
25.下面是两个立方体:
(1)请你在图1中以立方体顶点作为三角形顶点,画一个直角三角形ABC。
(2)在图2以立方体顶点作为三角形顶点,画一个等边三角形DEF。
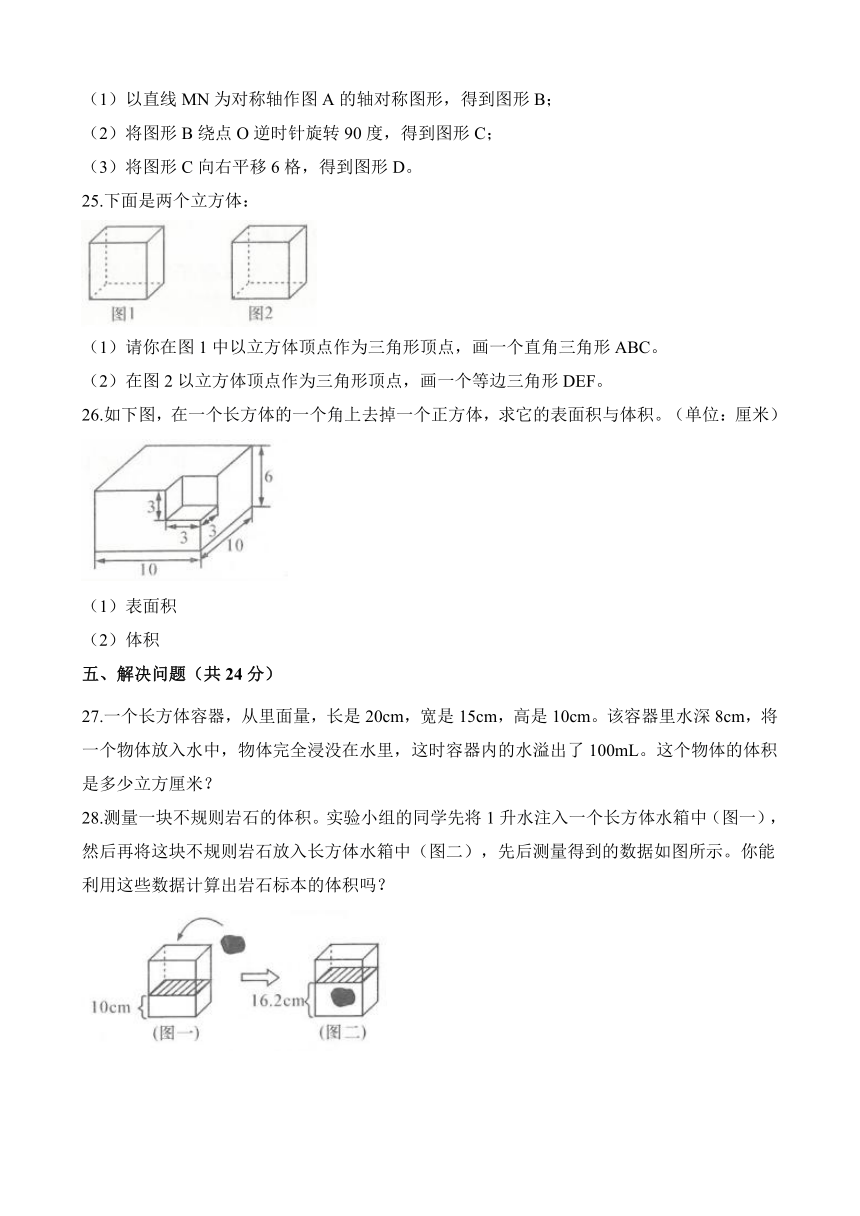
26.如下图,在一个长方体的一个角上去掉一个正方体,求它的表面积与体积。(单位:厘米)
(1)表面积
(2)体积
五、解决问题(共24分)
27.一个长方体容器,从里面量,长是20cm,宽是15cm,高是10cm。该容器里水深8cm,将一个物体放入水中,物体完全浸没在水里,这时容器内的水溢出了100mL。这个物体的体积是多少立方厘米?
28.测量一块不规则岩石的体积。实验小组的同学先将1升水注入一个长方体水箱中(图一),然后再将这块不规则岩石放入长方体水箱中(图二),先后测量得到的数据如图所示。你能利用这些数据计算出岩石标本的体积吗?
29.暑假里学校要给10个教室的顶面和四壁进行粉刷,每个教室的长9m、宽7m、高3m,已知每个教室的门窗面积之和是19m2 , 如果每平方米粉刷的费用8.5元,问这次粉刷学校共要支出多少钱?
30.有一块长32cm,宽16cm的长方形铁皮,通过折、割或焊等方法做出一个高为4cm的无盖长方体盒子,使这个盒子的容积尽可能的大,你会怎样设计?请画出示意图。
(1)我的设计是:长________cm,宽________cm,高4cm。
(2)我画的示意图:
(3)请列式计算出它的容积:
六、挑战题(附加10分)
31.把19个棱长为1厘米的正方体重叠在一起,按下图中的方式拼成一个立体图形。
(1)求这个立体图形的表面积。
(2)请分别画出从正面,上面,左面看到的图形。
(3)填一填
正方形:从正面看有________个,从上面看有________个,从左面看有________个。
计算:(________+________+________)×2=________,所以这个立体图形的表面积是________平方厘米。
答案解析部分
一、填空题(共22分)
1.【答案】 顺;90
【考点】一般时间与钟面指针的指向,旋转的三要素
【解析】【解答】360÷12=30(度),30×3=90(度),分针走的方向是顺时针方向。
故答案为:顺;90。
【分析】钟面上指针所走的方向是顺时针方向,圆周角是360度,被钟面平均分成12份,可以求出每一大格的是30度, 指针从12:05到12:20 ,分针走过3大格,就是旋转了3个30度,
2.【答案】 56;96;90
【考点】长方体的表面积,长方体的体积
【解析】【解答】(6+5+3)×4=14×4=56(分米)
6×5+6×3×2+5×3×2=30+36+30=96(平方分米)
6×5×3=90(立方分米)
故答案为:56;96;90。
【分析】求至少需要多少角钢,就是求长方体的棱长总和,长方体的棱长总和=(长+宽+高)×4;
求至少需要多少玻璃,就是求无盖长方体的表面积,无盖长方体的表面积=长×宽+长×高×2+宽×高×2。
求最多可以装多少水,就是求长方体的容积,长方体的体积=长×宽×高。
3.【答案】 45;27
【考点】正方体的表面积,正方体的体积
【解析】【解答】9÷3=3(cm),3×3×5=45(cm2),3×3×3=27(cm3)
故答案为:45;27。
【分析】因为折成的是一个最大的无盖正方体纸盒,而正方体的棱长都相等,所以可以知道把正方形的边长平均分成了3份,求出一份的长度,也就是正方体的棱长,这个无盖正方体的表面积=棱长×棱长×5,正方体的体积=棱长×棱长×棱长。
4.【答案】 10
【考点】长方体的特征
【解析】【解答】1米=100厘米,100÷4=25(cm),30÷2=15(cm),25-15=10(cm)
故答案为:10。
【分析】1米长的铁丝是长方体的棱长总和,长+宽+高=棱长总和÷4,长方体的底面周长=(长+宽)×2,所以长+宽=底面周长÷2,,再用长+宽+高-(长+宽)=高。
5.【答案】 60
【考点】长方体的特征,长方体的体积
【解析】【解答】解:4×5=20(cm2)? 3×5=15(cm2) ?长:5cm,宽:4cm,高:3cm? 体积为3×4×5=60(cm3)
故答案为:60。
【分析】长方体的底面积=长×宽,前面的面积=长×高,相邻的两个数是互质的,由此可以推出长方体的长、宽和高的长度,长方体的体积=长×宽×高。
6.【答案】 240;400;35
【考点】不规则物体的体积算法
【解析】【解答】80×3=240(cm3),80×(8-3)=400(cm3),240÷400=35。
故答案为:240;400;35。
【分析】减少的水的体积就是球的体积,小球的体积=底面积×拿走小球时减少的水深,大球的体积=底面积×(拿走两个球减少的水深-拿走小球减少的水深),求一个数是另一个数的几分之几,用一个数÷另一个数。
7.【答案】 (1)⑥⑨
(2)⑤⑥⑨
(3)①②④
【考点】从不同方向观察几何体
【解析】【解答】(1) 从正面看到的图形是 ,的有⑥⑨。
(2) 从左面看到的图形是 的有 ⑤⑥⑨ 。
(3) 从上面看到的图形是 的有 ①②④ 。
故答案为:(1) ⑥⑨ ;(2) ⑤⑥⑨ ;(3) ①②④ 。
【分析】(1) 从正面看到的图形是 ,说明这个几何体有3列,2层,且只有第二列上面有一个正方体。
(2) 从左面看到的图形是 ,说明这个几何体有2行,2层,且只有第一行上面有一个正方体。
(3) 从上面看到的图形是 ,说明这个几何体有1行,3列。
8.【答案】 180
【考点】长方体的体积,立方体的切拼
【解析】【解答】解:24÷4=6(dm2) ?3m=30dm? 6×30=180(dm3)
故答案为:180。
【分析】锯3段,就会增加4个底面的面积,这样可以求出一个底面的面积,再用底面积×高=长方体的体积。
9.【答案】 1000;10
【考点】正方体的体积
【解析】【解答】解:1dm3=1000cm3? 1000cm=10m。
故答案为:1000;10。
【分析】1dm3=1000cm3 ,说明1dm3的正方体中含有1000个1cm3的小正方体。
棱长是1cm的正方体,体积是1cm3 , 把1000块棱长是1cm的正方体排成一排,长就是1000cm,再来换算单位,1m=100cm。
10.【答案】 8;1
【考点】组合体露在外面的面
【解析】【解答】三面涂色的小正方体有8个,没有涂色的小正方体有1个。
故答案为:8;1。
【分析】这个大正方体由27个小正方体组成,其中在8个顶点的小正方体是涂了3个面,在12条棱中间的小正方体涂了2个面,在6个面心的小正方体涂了1个面,正方体最中间的1个小正方体只涂了1个面。
11.【答案】 5;7
【考点】根据观察到的图形确定几何体
【解析】【解答】最少的时候这个立体图形应该这样放:或或
需要2+1+1+1=5(个),最多的时候应该这样放:, 需要2+2+2+1=7(个)。
故答案为:5;7。
【分析】从上面看到的形状,可以确定这个立体图形有2行、3列,从左边看到的形状,可以确定这个立体图形有2行2层,只从上面和左边的图无法确定这个立体图形,最少的时候就是第2行的第二层只放1个正方体,最多的时候就是第2行到的第二层都摆满正方体。
二、判断题(共8分)
12.【答案】 错误
【考点】长方体的体积
【解析】【解答】 棱长之和相等的两个长方体,体积不一定也相等。
故答案为:错误。
【分析】长方体的棱长总和=(长+宽+高)×4,
假如两个长方体的棱长总和都是24厘米,
一个长方体的长、宽、高分别是3厘米,2厘米,1厘米,
则棱长之和是(3+2+1)×4=24(厘米);
体积是3×2×1=6(立方厘米);
另一个长方体长、宽、高分别是4厘米,1厘米,1厘米,
则棱长之和是(4+1+1)×4=24(厘米);
体积是4×1×1=4(立方厘米);
他们的棱长之和都是24厘米,但体积一个是6立方厘米,一个是4立方厘米,不相等。
13.【答案】 正确
【考点】正方形的面积,正方体的体积
【解析】【解答】1×1=1(平方米)
故答案为:正确。
【分析】棱长是1米的正方体体积是1立方米,正方体的占地面积就是它的底面积,底面积=棱长×棱长。
14.【答案】 正确 【考点】旋转与旋转现象
【解析】【解答】 电风扇扇叶的运动是一种旋转现象。
故答案为:正确。
【分析】 在平面内,一个图形绕着一个定点旋转一定的角度得到另一个图形的变化叫做旋转,这个定点叫做旋转中心,旋转的角度叫做旋转角。
15.【答案】 正确
【考点】长方体、正方体的容积
【解析】【解答】 体积是400立方厘米的保温杯,它的容积应当比400毫升小。
故答案为:正确。
【分析】体积是指物体所占空间的大小,计算体积时是从物体的外面去测量;容积是指容器(杯子、盒子、油桶等)所能容纳物体的大小(即内部体积),计算容积时是从物体的里面去测量。
三、选择题(共18分)
16.【答案】 D
【考点】作旋转后的图形
【解析】【解答】 绕它的中心顺时针旋转120°与原图形重合。
故答案为:D。
【分析】等边三角形的中心与它三个顶角的的连线正好把圆周角360°平均分成了3份,每一份就是120°,所以等边三角形需要绕它的中心顺时针旋转120°与原来的图形重合。
17.【答案】 C
【考点】根据观察到的图形确定几何体
【解析】【解答】 如果用数字表示积木从上面看所用的小正方体的个数 ,那么这个正方体应该为:。
故答案为:C。
【分析】从上面看的图,可以知道这个物体有两行三列,从正面看的图,可以知道这个物体两层,三列,且只有第1列第二层上面有一个正方体,第二、三列的第二层上面没有正方体,从左面看的图,可以知道这个物体有两行,两层,且只有第二行的第二层有正方体,第一行的第二层上面没有正方体,由此可以推出 从上面看所用的小正方体的个数 。
18.【答案】 C
【考点】组合体露在外面的面
【解析】【解答】A选项的立体图形重合了6个面,B选项的立体图形重合了6个面,C选项的立体图形重合率8个面,D选项的立体图形重合了6个面,C选项重合的面最多,它的表面积最小。
故答案为:C。
【分析】立体图形的表面积=4个正方体的表面积-重合部分的面积,因为四个选项中的图形都是由同样大小的4个正方体组成的,所以被减数相同,要差最小,那么减数必须最大,也就是图形重合部分的面积最多,再结合图分析每个选项重合的面积即可。
19.【答案】 A
【考点】长方体的特征
【解析】【解答】36÷4=9(cm)
故答案为:A。
【分析】长方体的棱长总和=(长+宽+高)×4, 相交于一个顶点的三条棱分别叫作长方体的长(、宽、高,所以长+宽+高=棱长总和÷4。
20.【答案】 C
【考点】长方体的体积,正方体的体积
【解析】【解答】解:2m=20dm,20÷2=10(个) ?4÷2=2(个) ?5÷2=2(个)……1(dm) ?最多能放10×2×2=40(个)。
故答案为:C。
【分析】看这个长方体可以放多少行,多少列,多少层的正方体,然后用行数×列数×层数=正方体的个数。
21.【答案】 A
【考点】从复式折线统计图获取信息,用图像表示变化关系
【解析】【解答】 一个人“平时”与“运动中”的心跳对比情况最理的是
故答案为:A。
【分析】 人在安静状态下的心率范围是60到100次/分 , 在运动时因为交感神经兴奋,心率可增加到160次/分,所以运动中的心跳会比平时的心跳快,体现在图中是虚线在实线的上面,无论在“平时”还是在“运动中”,心跳都不会出现大幅度的变化。
四、计算与操作(共28分)
22.【答案】 (1)解:20×5=100(立方分米)
(2)解:8×12×10+5×3×10=1110(立方分米)
【考点】长方形的面积,组合体的体积的巧算
【解析】【分析】(1)长方体的体积=底面积×高。
(2)立体图形的体积=小长方体的体积+大长方体的体积,长方体的体积=长×宽×高。
23.【答案】 解:12×(18-12)×6=432(cm3)
【考点】长方体的展开图,长方体的体积
【解析】【分析】观察长方体的展开图可知:这个长方体的长是12cm,宽是6cm,高是(18-12)cm,长方体的体积=长×宽×高。
24.【答案】 (1)
(2)
(3)
【考点】补全轴对称图形,作平移后的图形,作旋转后的图形
【解析】【分析】(1)轴对称图形到对称轴的距离相等。
(2)图形在旋转的时候,旋转中心不动,形状和大小不变,位置发生变化,注意旋转方向是图形B逆时针。
(3)图形在平移时,形状和大小不变,位置发生变化。
25.【答案】 (1)解:
(2)解:
【考点】等边三角形认识及特征,正方体的特征
【解析】【分析】立方体的每个面都是大小相同的正方形,把任意一个面的对角线连接起来,就可以得到直角三角形。这六个面的对角线的长度都相同,任意三条对角线能够围成的三角形就是等边三角形。
26.【答案】 (1)解:表面积:(10×10+10×6+6×10)×2=440(cm2)
(2)解:体积:10×10×6-3×3×3=573(cm3)
【考点】组合体的表面积,长方体的体积,正方体的体积
【解析】【分析】(1) 在一个长方体的一个角上去掉一个正方体,会少了三个正方形的面积,正好又会露出来三个同样大小的正方形的面积,这样,这个图形的表面积还是原来长方体的表面积,长方体的表面积=(长×宽+长×高+宽×高)×2。
(2)这个几何体的体积=长方体的体积-正方体的体积,长方体的体积=长×宽×高,正方体的体积=棱长×棱长×棱长。
五、解决问题(共24分)
27.【答案】 解:(10-8)×20×15=600(cm3)
100mL=100cm3
600+100=700(cm3)
答:这个物体的体积是700cm3。
【考点】不规则物体的体积算法
【解析】【分析】这个物体的体积=上升部分水的体积+溢出水的体积,上升部分水的体积=长×宽×水上升的高度,把溢出水的体积换算成立方厘米,1mL=1cm3 , 再代入计算即可得到物体的体积。
28.【答案】 解:1升=1(dm3)=1000(cm3)
1000÷10×16.2-1000=620(cm3)
【考点】不规则物体的体积算法
【解析】【分析】岩石标本的体积=岩石和水的体积-水的体积,只加入1L水时,水深10cm,可以求出容器的底面积,底面积=水的体积÷水深,岩石和水的体积=底面积×加入岩石后的水深,再代入数字计算,就可以得到岩石标本的体积。
29.【答案】 解:[9×7+(7×3+9×3)×2-19]×10×8.5=11900(元)
答:这次粉刷学校共要支出11900元。
【考点】长方体的表面积
【解析】【分析】每个教室需要粉刷的面积=(长×宽+长×高×2+宽×高×2)-门窗的面积, 10间教室的粉刷面积就是每个教室粉刷面积的10倍,每平方米粉刷的费用8.5元 ,一共有多少平方米的面积需要粉刷,就有多少个8.5元。
30.【答案】 (1)24;8
(2)解:
(3)解:32-2×4=24(cm)
16-2×4=8(cm)
24×8×4=768(cm3)
答:它的容积是768cm3。
【考点】长方体的体积
【解析】【解答】解:(1)长:32-4×2=24(cm),宽:16-4×2=8(cm)
(2)
(3)24×8×4=768(cm3)
【分析】这个无盖长方体的长,是在原来长方形的两端各剪去一个4cm,长方体的宽,是在原来长方形宽的两端各剪去一个4cm,这样就相当于在原来长方形的四个角剪去了边长是4cm的小正方形,这个长方体的体积=长×宽×高。
六、挑战题(附加10分)
31.【答案】 (1)解:1×1=1(cm2)
1×(8+10+9+8+10+9)=54(cm2)
(2)
(3)10;9;8;10;9;8;54;54
【考点】从不同方向观察几何体,组合体露在外面的面
【解析】【解答】解:(3)从正面看有10个面,从上面看有9个面,从左面看有8个面,(10+9+8)×2=54,(cm2),所以这个立体图形的表面积是54平方厘米。
【分析】棱长是1cm的正方体,每个面的面积都是1cm2 , 有多少个面在外面,这个立体图形的表面积就是多少个1cm2 , 通过观察分析可以知道,左面和右面各有8个面在外面,正面和后面各有10个面在外面,上面和下面各有9个面在外面,这样就可以求出这个立体图形的表面积。
一、填空题(共22分)
1.钟面上,指针从12:05到12:20,分针按________时针旋转了________度。
2.做一个长6分米,宽5分米,高3分米的无盖鱼缸,用角钢做它的框架,至少需要角钢________分米,至少需要玻璃________平方分米,最多可装水________立方分米。
3.如图,把一张边长9厘米的正方形纸,剪成一个“十字形”图案,折成了一个最大的无盖正方体纸盒。这个正方体纸盒用了________平方厘米的纸,体积是________立方厘米。
4.用一根长1米的铁丝焊接成一个长方体框架,它的底面周长是30厘米,高是________厘米。
5.一个长方体的底面积为20平方厘米,前面面积为15平方厘米,且相交于一个顶点的三条棱彼此互质,这个长方体的体积是________立方厘米。
6.一个长方体容器的底面积是80cm2 , 浸没着大,小两个球时,水面正好到容器口。现在先后取出这两个球,水面变化情况如下图所示。小球的体积是________?cm3 , 大球的体积是________?cm3。小球的体积是大球的________。
7.?
(1)从正面看到的图形是 的有________;
(2)从左面看到的图形是 的有________;
(3)从上面看到的图形是 的有________。
8.把一根长3m的长方体木材锯成3段(如图),表面积增加了24dm2 , 这根木材原来的体积是________?dm3。
9.用体积1cm3的小正方体堆成的一个体积是1dm3的大正方体,需要________块,如果把这些小正方体紧挨着排成一排,长________?m。
10.下图是用小正方体拼成的大正方体,在它的表面涂上颜色。三面涂色的小正方体有________个;没有涂色的小正方体有________个。
11.一个用小立方块摆成的立体图形,从上面看形状是 ,从左面看形状是 ,摆这个立体图形至少用________个小立方块,最多可以用________个小立方块。
二、判断题(共8分)
12.棱长之和相等的两个长方体,体积一定也相等。(??? )
13.把体积为1立方米的正方体放在地上,它的占地面积就是1平方米。(??? )
14.电风扇扇叶的运动是一种旋转现象。(??? )
15.体积是400立方厘米的保温杯,它的容积应当比400毫升小。(??? )
三、选择题(共18分)
16.老师要求将下面图1中的每个图形都绕它的中心顺时针旋转90°后画下来。图2是小强画的,但有一个图他画错了,这个图形是(??? )。
A.?A???????????????????????????????????????????B.?B?????????????????????????????????C.?C???????????????????????????????????????????D.?D
17.有一些立方体积木,根据不同方向看到的形状如图,如果用数字表示积木从上面看所用的小正方体的个数,那么正确的是(??? )。
A.?????????????????????B.????????????????????C.?????????????????????D.?
18.由4个小正方体搭拼而成的下面四个立体图形中,表面积最小的是(??? )。
A.?????????????????????????????B.????????????????????????????C.?????????????????????????????D.?
19.一个长方体的所有棱长之和是36厘米,则相交于一个顶点的所有棱长之和是(??? )。
A.?9厘米?????????????????????????????????B.?12厘米????????????????????C.?18厘米?????????????????????????????????D.?3厘米
20.一个长2m,宽4dm,高5dm的长方体盒子。最多能放(??? )个棱长为2dm的正方体木块。
A.?5个?????????????????????????????????????B.?20个?????????????????????????C.?40个?????????????????????????????????????D.?50个
21.下图中,表示一个人“平时”与“运动中”的心跳对比情况最合理的是(??? )。
A.?????????????B.?
C.??????????????D.?
四、计算与操作(共28分)
22.按要求计算。
(1)
底面积是20平方分米
体积:
(2)(单位:分米)
体积:
23.根据下面的长方体的展开图所标出的长度,求这个长方体的体积是多少?
24.按要求作图:
(1)以直线MN为对称轴作图A的轴对称图形,得到图形B;
(2)将图形B绕点O逆时针旋转90度,得到图形C;
(3)将图形C向右平移6格,得到图形D。
25.下面是两个立方体:
(1)请你在图1中以立方体顶点作为三角形顶点,画一个直角三角形ABC。
(2)在图2以立方体顶点作为三角形顶点,画一个等边三角形DEF。
26.如下图,在一个长方体的一个角上去掉一个正方体,求它的表面积与体积。(单位:厘米)
(1)表面积
(2)体积
五、解决问题(共24分)
27.一个长方体容器,从里面量,长是20cm,宽是15cm,高是10cm。该容器里水深8cm,将一个物体放入水中,物体完全浸没在水里,这时容器内的水溢出了100mL。这个物体的体积是多少立方厘米?
28.测量一块不规则岩石的体积。实验小组的同学先将1升水注入一个长方体水箱中(图一),然后再将这块不规则岩石放入长方体水箱中(图二),先后测量得到的数据如图所示。你能利用这些数据计算出岩石标本的体积吗?
29.暑假里学校要给10个教室的顶面和四壁进行粉刷,每个教室的长9m、宽7m、高3m,已知每个教室的门窗面积之和是19m2 , 如果每平方米粉刷的费用8.5元,问这次粉刷学校共要支出多少钱?
30.有一块长32cm,宽16cm的长方形铁皮,通过折、割或焊等方法做出一个高为4cm的无盖长方体盒子,使这个盒子的容积尽可能的大,你会怎样设计?请画出示意图。
(1)我的设计是:长________cm,宽________cm,高4cm。
(2)我画的示意图:
(3)请列式计算出它的容积:
六、挑战题(附加10分)
31.把19个棱长为1厘米的正方体重叠在一起,按下图中的方式拼成一个立体图形。
(1)求这个立体图形的表面积。
(2)请分别画出从正面,上面,左面看到的图形。
(3)填一填
正方形:从正面看有________个,从上面看有________个,从左面看有________个。
计算:(________+________+________)×2=________,所以这个立体图形的表面积是________平方厘米。
答案解析部分
一、填空题(共22分)
1.【答案】 顺;90
【考点】一般时间与钟面指针的指向,旋转的三要素
【解析】【解答】360÷12=30(度),30×3=90(度),分针走的方向是顺时针方向。
故答案为:顺;90。
【分析】钟面上指针所走的方向是顺时针方向,圆周角是360度,被钟面平均分成12份,可以求出每一大格的是30度, 指针从12:05到12:20 ,分针走过3大格,就是旋转了3个30度,
2.【答案】 56;96;90
【考点】长方体的表面积,长方体的体积
【解析】【解答】(6+5+3)×4=14×4=56(分米)
6×5+6×3×2+5×3×2=30+36+30=96(平方分米)
6×5×3=90(立方分米)
故答案为:56;96;90。
【分析】求至少需要多少角钢,就是求长方体的棱长总和,长方体的棱长总和=(长+宽+高)×4;
求至少需要多少玻璃,就是求无盖长方体的表面积,无盖长方体的表面积=长×宽+长×高×2+宽×高×2。
求最多可以装多少水,就是求长方体的容积,长方体的体积=长×宽×高。
3.【答案】 45;27
【考点】正方体的表面积,正方体的体积
【解析】【解答】9÷3=3(cm),3×3×5=45(cm2),3×3×3=27(cm3)
故答案为:45;27。
【分析】因为折成的是一个最大的无盖正方体纸盒,而正方体的棱长都相等,所以可以知道把正方形的边长平均分成了3份,求出一份的长度,也就是正方体的棱长,这个无盖正方体的表面积=棱长×棱长×5,正方体的体积=棱长×棱长×棱长。
4.【答案】 10
【考点】长方体的特征
【解析】【解答】1米=100厘米,100÷4=25(cm),30÷2=15(cm),25-15=10(cm)
故答案为:10。
【分析】1米长的铁丝是长方体的棱长总和,长+宽+高=棱长总和÷4,长方体的底面周长=(长+宽)×2,所以长+宽=底面周长÷2,,再用长+宽+高-(长+宽)=高。
5.【答案】 60
【考点】长方体的特征,长方体的体积
【解析】【解答】解:4×5=20(cm2)? 3×5=15(cm2) ?长:5cm,宽:4cm,高:3cm? 体积为3×4×5=60(cm3)
故答案为:60。
【分析】长方体的底面积=长×宽,前面的面积=长×高,相邻的两个数是互质的,由此可以推出长方体的长、宽和高的长度,长方体的体积=长×宽×高。
6.【答案】 240;400;35
【考点】不规则物体的体积算法
【解析】【解答】80×3=240(cm3),80×(8-3)=400(cm3),240÷400=35。
故答案为:240;400;35。
【分析】减少的水的体积就是球的体积,小球的体积=底面积×拿走小球时减少的水深,大球的体积=底面积×(拿走两个球减少的水深-拿走小球减少的水深),求一个数是另一个数的几分之几,用一个数÷另一个数。
7.【答案】 (1)⑥⑨
(2)⑤⑥⑨
(3)①②④
【考点】从不同方向观察几何体
【解析】【解答】(1) 从正面看到的图形是 ,的有⑥⑨。
(2) 从左面看到的图形是 的有 ⑤⑥⑨ 。
(3) 从上面看到的图形是 的有 ①②④ 。
故答案为:(1) ⑥⑨ ;(2) ⑤⑥⑨ ;(3) ①②④ 。
【分析】(1) 从正面看到的图形是 ,说明这个几何体有3列,2层,且只有第二列上面有一个正方体。
(2) 从左面看到的图形是 ,说明这个几何体有2行,2层,且只有第一行上面有一个正方体。
(3) 从上面看到的图形是 ,说明这个几何体有1行,3列。
8.【答案】 180
【考点】长方体的体积,立方体的切拼
【解析】【解答】解:24÷4=6(dm2) ?3m=30dm? 6×30=180(dm3)
故答案为:180。
【分析】锯3段,就会增加4个底面的面积,这样可以求出一个底面的面积,再用底面积×高=长方体的体积。
9.【答案】 1000;10
【考点】正方体的体积
【解析】【解答】解:1dm3=1000cm3? 1000cm=10m。
故答案为:1000;10。
【分析】1dm3=1000cm3 ,说明1dm3的正方体中含有1000个1cm3的小正方体。
棱长是1cm的正方体,体积是1cm3 , 把1000块棱长是1cm的正方体排成一排,长就是1000cm,再来换算单位,1m=100cm。
10.【答案】 8;1
【考点】组合体露在外面的面
【解析】【解答】三面涂色的小正方体有8个,没有涂色的小正方体有1个。
故答案为:8;1。
【分析】这个大正方体由27个小正方体组成,其中在8个顶点的小正方体是涂了3个面,在12条棱中间的小正方体涂了2个面,在6个面心的小正方体涂了1个面,正方体最中间的1个小正方体只涂了1个面。
11.【答案】 5;7
【考点】根据观察到的图形确定几何体
【解析】【解答】最少的时候这个立体图形应该这样放:或或
需要2+1+1+1=5(个),最多的时候应该这样放:, 需要2+2+2+1=7(个)。
故答案为:5;7。
【分析】从上面看到的形状,可以确定这个立体图形有2行、3列,从左边看到的形状,可以确定这个立体图形有2行2层,只从上面和左边的图无法确定这个立体图形,最少的时候就是第2行的第二层只放1个正方体,最多的时候就是第2行到的第二层都摆满正方体。
二、判断题(共8分)
12.【答案】 错误
【考点】长方体的体积
【解析】【解答】 棱长之和相等的两个长方体,体积不一定也相等。
故答案为:错误。
【分析】长方体的棱长总和=(长+宽+高)×4,
假如两个长方体的棱长总和都是24厘米,
一个长方体的长、宽、高分别是3厘米,2厘米,1厘米,
则棱长之和是(3+2+1)×4=24(厘米);
体积是3×2×1=6(立方厘米);
另一个长方体长、宽、高分别是4厘米,1厘米,1厘米,
则棱长之和是(4+1+1)×4=24(厘米);
体积是4×1×1=4(立方厘米);
他们的棱长之和都是24厘米,但体积一个是6立方厘米,一个是4立方厘米,不相等。
13.【答案】 正确
【考点】正方形的面积,正方体的体积
【解析】【解答】1×1=1(平方米)
故答案为:正确。
【分析】棱长是1米的正方体体积是1立方米,正方体的占地面积就是它的底面积,底面积=棱长×棱长。
14.【答案】 正确 【考点】旋转与旋转现象
【解析】【解答】 电风扇扇叶的运动是一种旋转现象。
故答案为:正确。
【分析】 在平面内,一个图形绕着一个定点旋转一定的角度得到另一个图形的变化叫做旋转,这个定点叫做旋转中心,旋转的角度叫做旋转角。
15.【答案】 正确
【考点】长方体、正方体的容积
【解析】【解答】 体积是400立方厘米的保温杯,它的容积应当比400毫升小。
故答案为:正确。
【分析】体积是指物体所占空间的大小,计算体积时是从物体的外面去测量;容积是指容器(杯子、盒子、油桶等)所能容纳物体的大小(即内部体积),计算容积时是从物体的里面去测量。
三、选择题(共18分)
16.【答案】 D
【考点】作旋转后的图形
【解析】【解答】 绕它的中心顺时针旋转120°与原图形重合。
故答案为:D。
【分析】等边三角形的中心与它三个顶角的的连线正好把圆周角360°平均分成了3份,每一份就是120°,所以等边三角形需要绕它的中心顺时针旋转120°与原来的图形重合。
17.【答案】 C
【考点】根据观察到的图形确定几何体
【解析】【解答】 如果用数字表示积木从上面看所用的小正方体的个数 ,那么这个正方体应该为:。
故答案为:C。
【分析】从上面看的图,可以知道这个物体有两行三列,从正面看的图,可以知道这个物体两层,三列,且只有第1列第二层上面有一个正方体,第二、三列的第二层上面没有正方体,从左面看的图,可以知道这个物体有两行,两层,且只有第二行的第二层有正方体,第一行的第二层上面没有正方体,由此可以推出 从上面看所用的小正方体的个数 。
18.【答案】 C
【考点】组合体露在外面的面
【解析】【解答】A选项的立体图形重合了6个面,B选项的立体图形重合了6个面,C选项的立体图形重合率8个面,D选项的立体图形重合了6个面,C选项重合的面最多,它的表面积最小。
故答案为:C。
【分析】立体图形的表面积=4个正方体的表面积-重合部分的面积,因为四个选项中的图形都是由同样大小的4个正方体组成的,所以被减数相同,要差最小,那么减数必须最大,也就是图形重合部分的面积最多,再结合图分析每个选项重合的面积即可。
19.【答案】 A
【考点】长方体的特征
【解析】【解答】36÷4=9(cm)
故答案为:A。
【分析】长方体的棱长总和=(长+宽+高)×4, 相交于一个顶点的三条棱分别叫作长方体的长(、宽、高,所以长+宽+高=棱长总和÷4。
20.【答案】 C
【考点】长方体的体积,正方体的体积
【解析】【解答】解:2m=20dm,20÷2=10(个) ?4÷2=2(个) ?5÷2=2(个)……1(dm) ?最多能放10×2×2=40(个)。
故答案为:C。
【分析】看这个长方体可以放多少行,多少列,多少层的正方体,然后用行数×列数×层数=正方体的个数。
21.【答案】 A
【考点】从复式折线统计图获取信息,用图像表示变化关系
【解析】【解答】 一个人“平时”与“运动中”的心跳对比情况最理的是
故答案为:A。
【分析】 人在安静状态下的心率范围是60到100次/分 , 在运动时因为交感神经兴奋,心率可增加到160次/分,所以运动中的心跳会比平时的心跳快,体现在图中是虚线在实线的上面,无论在“平时”还是在“运动中”,心跳都不会出现大幅度的变化。
四、计算与操作(共28分)
22.【答案】 (1)解:20×5=100(立方分米)
(2)解:8×12×10+5×3×10=1110(立方分米)
【考点】长方形的面积,组合体的体积的巧算
【解析】【分析】(1)长方体的体积=底面积×高。
(2)立体图形的体积=小长方体的体积+大长方体的体积,长方体的体积=长×宽×高。
23.【答案】 解:12×(18-12)×6=432(cm3)
【考点】长方体的展开图,长方体的体积
【解析】【分析】观察长方体的展开图可知:这个长方体的长是12cm,宽是6cm,高是(18-12)cm,长方体的体积=长×宽×高。
24.【答案】 (1)
(2)
(3)
【考点】补全轴对称图形,作平移后的图形,作旋转后的图形
【解析】【分析】(1)轴对称图形到对称轴的距离相等。
(2)图形在旋转的时候,旋转中心不动,形状和大小不变,位置发生变化,注意旋转方向是图形B逆时针。
(3)图形在平移时,形状和大小不变,位置发生变化。
25.【答案】 (1)解:
(2)解:
【考点】等边三角形认识及特征,正方体的特征
【解析】【分析】立方体的每个面都是大小相同的正方形,把任意一个面的对角线连接起来,就可以得到直角三角形。这六个面的对角线的长度都相同,任意三条对角线能够围成的三角形就是等边三角形。
26.【答案】 (1)解:表面积:(10×10+10×6+6×10)×2=440(cm2)
(2)解:体积:10×10×6-3×3×3=573(cm3)
【考点】组合体的表面积,长方体的体积,正方体的体积
【解析】【分析】(1) 在一个长方体的一个角上去掉一个正方体,会少了三个正方形的面积,正好又会露出来三个同样大小的正方形的面积,这样,这个图形的表面积还是原来长方体的表面积,长方体的表面积=(长×宽+长×高+宽×高)×2。
(2)这个几何体的体积=长方体的体积-正方体的体积,长方体的体积=长×宽×高,正方体的体积=棱长×棱长×棱长。
五、解决问题(共24分)
27.【答案】 解:(10-8)×20×15=600(cm3)
100mL=100cm3
600+100=700(cm3)
答:这个物体的体积是700cm3。
【考点】不规则物体的体积算法
【解析】【分析】这个物体的体积=上升部分水的体积+溢出水的体积,上升部分水的体积=长×宽×水上升的高度,把溢出水的体积换算成立方厘米,1mL=1cm3 , 再代入计算即可得到物体的体积。
28.【答案】 解:1升=1(dm3)=1000(cm3)
1000÷10×16.2-1000=620(cm3)
【考点】不规则物体的体积算法
【解析】【分析】岩石标本的体积=岩石和水的体积-水的体积,只加入1L水时,水深10cm,可以求出容器的底面积,底面积=水的体积÷水深,岩石和水的体积=底面积×加入岩石后的水深,再代入数字计算,就可以得到岩石标本的体积。
29.【答案】 解:[9×7+(7×3+9×3)×2-19]×10×8.5=11900(元)
答:这次粉刷学校共要支出11900元。
【考点】长方体的表面积
【解析】【分析】每个教室需要粉刷的面积=(长×宽+长×高×2+宽×高×2)-门窗的面积, 10间教室的粉刷面积就是每个教室粉刷面积的10倍,每平方米粉刷的费用8.5元 ,一共有多少平方米的面积需要粉刷,就有多少个8.5元。
30.【答案】 (1)24;8
(2)解:
(3)解:32-2×4=24(cm)
16-2×4=8(cm)
24×8×4=768(cm3)
答:它的容积是768cm3。
【考点】长方体的体积
【解析】【解答】解:(1)长:32-4×2=24(cm),宽:16-4×2=8(cm)
(2)
(3)24×8×4=768(cm3)
【分析】这个无盖长方体的长,是在原来长方形的两端各剪去一个4cm,长方体的宽,是在原来长方形宽的两端各剪去一个4cm,这样就相当于在原来长方形的四个角剪去了边长是4cm的小正方形,这个长方体的体积=长×宽×高。
六、挑战题(附加10分)
31.【答案】 (1)解:1×1=1(cm2)
1×(8+10+9+8+10+9)=54(cm2)
(2)
(3)10;9;8;10;9;8;54;54
【考点】从不同方向观察几何体,组合体露在外面的面
【解析】【解答】解:(3)从正面看有10个面,从上面看有9个面,从左面看有8个面,(10+9+8)×2=54,(cm2),所以这个立体图形的表面积是54平方厘米。
【分析】棱长是1cm的正方体,每个面的面积都是1cm2 , 有多少个面在外面,这个立体图形的表面积就是多少个1cm2 , 通过观察分析可以知道,左面和右面各有8个面在外面,正面和后面各有10个面在外面,上面和下面各有9个面在外面,这样就可以求出这个立体图形的表面积。
