五年级下册数学试题-总复习三:解决问题 人教版(含解析)
文档属性
| 名称 | 五年级下册数学试题-总复习三:解决问题 人教版(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 279.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-23 00:00:00 | ||
图片预览



文档简介
人教版数学2019-2020学年五年级下册总复习三:解决问题
一、填空题(共12分)(共6题;共12分)
1.把一个3平方米的花圃分成相等的4份,分别种上兰花、菊花、月季花和玫瑰花。兰花的种植面积占总面积的________,玫瑰花的种植面积是________平方米。
2.下图的秤最多能称15kg的物品。一个西瓜放在托盘上面后,仪表指针沿顺时针方向旋转90°。这个西瓜重________ kg。
3.把四块棱长2厘米的正方体粘成一个长方体,它的表面积最多会减少________平方厘米。
4.五(1)班有40多名同学,参加广播操比赛时正好排成每行8人或每行12人,且没有人员多余或不足,五(1)班有________人参加广播操比赛。
5.13×4 + 14×5 + 15×6 + 16×7 + 17×8 + 18×9 + 19×10 =________
6.大、中、小三个杯子互相倒水,用3个中杯可以把大杯倒满,用5个小杯子也能将大杯倒满。现在用中杯、小杯各往大杯中倒一次,此时大杯中的水是整个杯子的________。
二、选择题(共8分)
7.“助残日”爱心捐款活动中,徐老师捐出了月工资的 38 ,王老师也捐出了月工资的 38 。比较两位老师捐的钱,结果是(??? )。
A.?两人捐的一样多???????????????B.?徐老师捐的多???????????????C.?王老师捐的多???????????????D.?无法确定谁捐的多
8.小学生聪聪在一次满分为100分的科学知识竞赛中取得了好成绩,已知他的得分、名次及年龄均为质数,且三者之和等于110,那么聪聪得了第(??? )名。
A.?1???????????????????????????????????????????B.?2??????????????????????????????????????????C.?3???????????????????????????????????????????D.?5
9.有一架两盘天平,只有5克和30克砝码各一个,现在要把300克盐分成3等份,问最少需要用天平称(??? )次。
A.?2???????????????????????????????????????????B.?3??????????????????????????????????????????C.?4???????????????????????????????????????????D.?5
10.如图,三个棱长分别是1厘米、2厘米、3厘米的正方体叠放在一起,整个图形的表面积是(??? )平方厘米。
A.?70?????????????????????????????????????????B.?74?????????????????????????????????????????C.?78?????????????????????????????????????????D.?80
三、只列式,不计算(共12分)
11.只列式,不计算
(1)一个长方体的长、宽、高分别是5分米、3分米和2分米。如果把这个长方体放在地面上,最大的占地面积是多少平方分米?
(2)植树节到了,五(2)班40名学生有29名参加植树活动。没有参加植树活动的人数占全班学生人数的几分之几?
(3)小明家有一块 45 公顷的菜地。爸爸打算用它的 215 种油菜,用它的 15 种西红柿。还剩下这块地的几分之几没有种?
四、解决问题(共68分)
12.学校举行数学竞赛,获一、二等奖的占获奖总人数的 35 ,获二、三等奖的占获奖总人数的 710 ,获二等奖的占获奖总人数的几分之几?
13.操场跑道,小亮跑一圈要6分钟,爸爸跑一圈要3分钟,妈妈跑一圈要4分钟。如果小亮和妈妈同时起跑,至少多少分钟后两人在起点再次相遇?此时妈妈比小亮多跑了多少圈?
14.把一块棱长是8厘米的立方体钢坯,锻造成一块长16厘米,宽5厘米的长方体钢板,这块钢板有多厚?(损耗不计)
15.一根长1.5米的长方体木料,底面是正方形,把木料锯成两段后,表面积增加0.18平方分米,求原来木料的表面积。
16.放学后,老师要尽快通知全班63人第二天穿校服,如果用打电话的方式,每分钟通知1人。
(1)通知所有人至少需要多少分钟?
(2)按上面的方法,8分钟最多能通知到多少人?
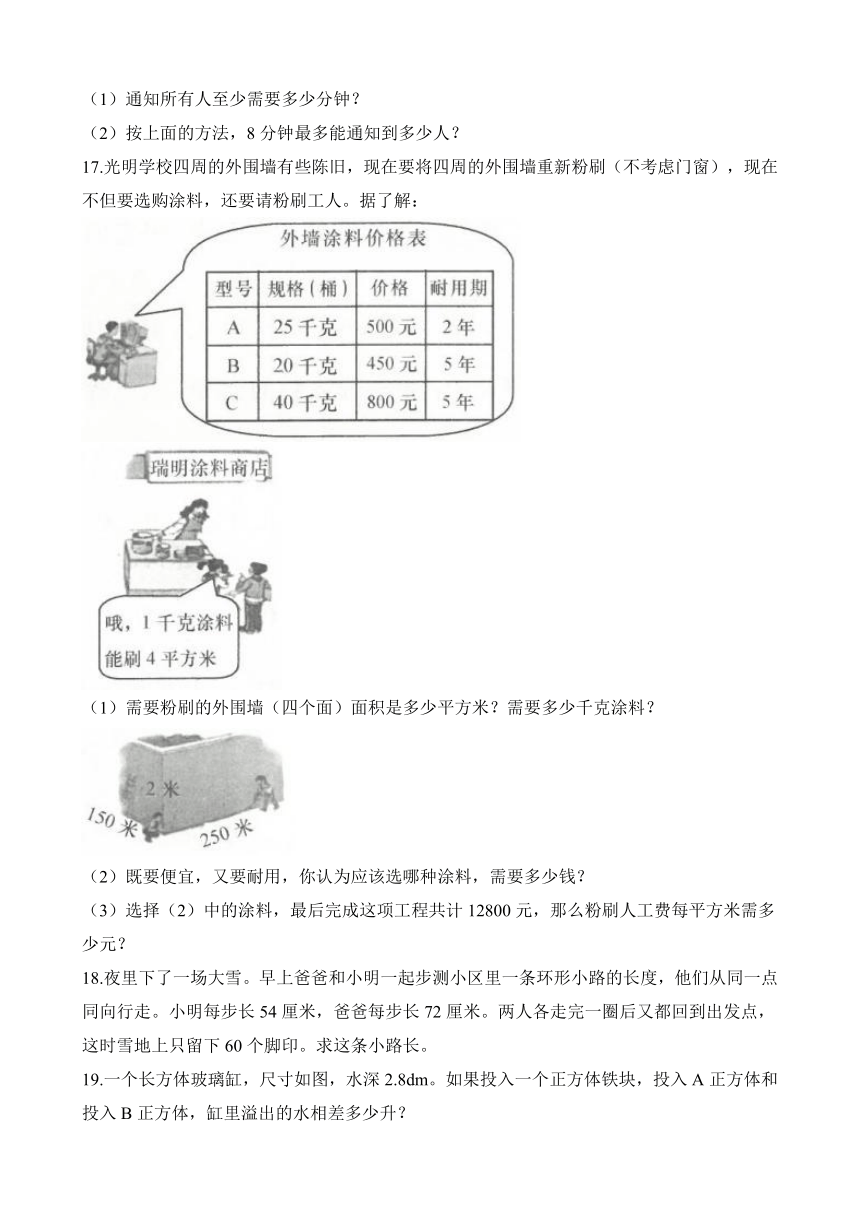
17.光明学校四周的外围墙有些陈旧,现在要将四周的外围墙重新粉刷(不考虑门窗),现在不但要选购涂料,还要请粉刷工人。据了解:
(1)需要粉刷的外围墙(四个面)面积是多少平方米?需要多少千克涂料?
(2)既要便宜,又要耐用,你认为应该选哪种涂料,需要多少钱?
(3)选择(2)中的涂料,最后完成这项工程共计12800元,那么粉刷人工费每平方米需多少元?
18.夜里下了一场大雪。早上爸爸和小明一起步测小区里一条环形小路的长度,他们从同一点同向行走。小明每步长54厘米,爸爸每步长72厘米。两人各走完一圈后又都回到出发点,这时雪地上只留下60个脚印。求这条小路长。
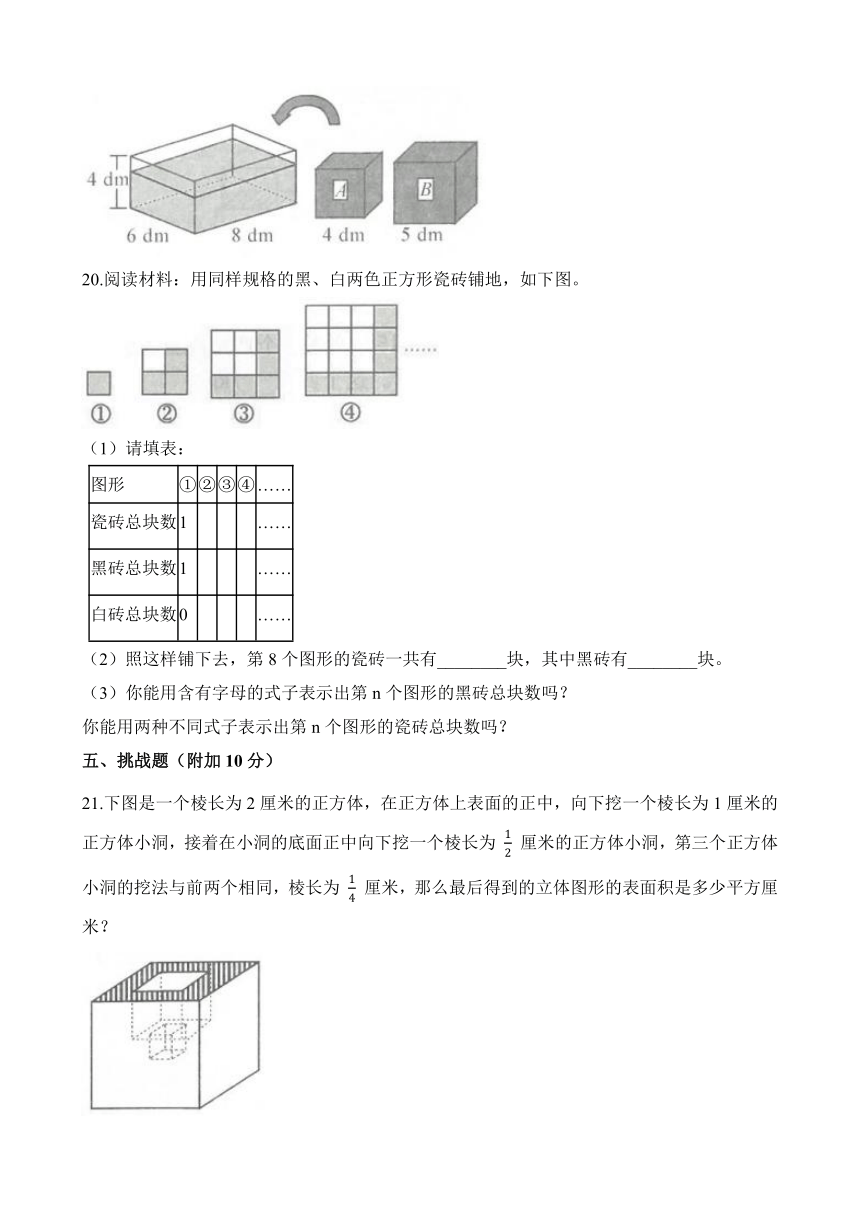
19.一个长方体玻璃缸,尺寸如图,水深2.8dm。如果投入一个正方体铁块,投入A正方体和投入B正方体,缸里溢出的水相差多少升?
20.阅读材料:用同样规格的黑、白两色正方形瓷砖铺地,如下图。
(1)请填表:
图形
①
②
③
④
……
瓷砖总块数
1
……
黑砖总块数
1
……
白砖总块数
0
……
(2)照这样铺下去,第8个图形的瓷砖一共有________块,其中黑砖有________块。
(3)你能用含有字母的式子表示出第n个图形的黑砖总块数吗?
你能用两种不同式子表示出第n个图形的瓷砖总块数吗?
五、挑战题(附加10分)
21.下图是一个棱长为2厘米的正方体,在正方体上表面的正中,向下挖一个棱长为1厘米的正方体小洞,接着在小洞的底面正中向下挖一个棱长为 12 厘米的正方体小洞,第三个正方体小洞的挖法与前两个相同,棱长为 14 厘米,那么最后得到的立体图形的表面积是多少平方厘米?
答案解析部分
一、填空题(共12分)
1.【答案】 14;34
【考点】分数及其意义,分数与除法的关系
【解析】【解答】1÷4=14 , 3÷4=34(平方米)
故答案为:14;34。
【分析】把花圃的面积看作单位“1”,把单位“1”平均分成4份,每份占总面积的14 , 兰花的面积只有这样的一份,也就是1个14。把3平方米的花圃平均分成4份,每份的面积是34平方米,玫瑰花的面积只有这样的一份也就是1个34平方米。
2.【答案】 3.75
【考点】将简单图形平移或旋转一定的度数
【解析】【解答】360÷15=24(度),90÷24=3.75(kg)
故答案为:3.75。
【分析】圆周角是360度,被平均分成15份,一份就是24度。 仪表指针沿顺时针方向旋转90° ,90度中含有几个24度,指针就转动几格,也就是西瓜重几千克。
3.【答案】 32
【考点】立方体的切拼
【解析】【解答】2×2×8=32(平方厘米)
故答案为:32。
【分析】要使表面积减少最多,那么重合的面必须最多,因此这4块正方体应该这样摆放:, 重合的面有8个正方形,每个正方形的面积是(2×2)平方厘米。
4.【答案】 48
【考点】最小公倍数的应用
【解析】【解答】 8和12的最小公倍数为:24,24×2=48(人),40<48<50.
故答案为:48。
【分析】参加广播操比赛时正好排成每行8人或每行12人, 说明参加广播操比赛的人数是8和12的公倍数,而 五(1)班的学生有40多,所以只能是48人。
5.【答案】 730
【考点】分数的拆项,巧算分数和
【解析】【解答】原式= 13 - 14 + 14 - 15 + 15 - 16 + 16 - 17 +…+ 19 - 110 = 13 - 110 = 730
故答案为:730。
【分析】观察算式可以知道,每个分数的分母中的两个因数是相邻的自然数,并且第二个数是下一个分数分母的起始数,那么可以得到1n×(n+1)=1n-1n+1 , 可以把每个分数拆成这样的形式,再进行计算。
6.【答案】 815
【考点】最小公倍数的应用
【解析】【解答】3和5的最小公倍数是15,15÷3=5,15÷5=3,(5+3)÷15=815。
故答案为:815。
【分析】用3个中杯可以把大杯倒满,用5个小杯子也能将大杯倒满,说明大杯的容量是3和5的公倍数, 再算出中杯一次可以倒入大杯的量,小杯一次可以倒入大杯的量,最后用(中杯一次的量+小杯一次的量)÷大杯的量= 大杯中的水是整个杯子的几分之几。
二、选择题(共8分)
7.【答案】 D
【考点】单位“1”的认识及确定
【解析】【解答】因为徐老师月工资和王老师月工资分别是多少,没有告诉,所以无法比较两位老师捐钱的多少。
故答案为:D。
【分析】第一个“38”的单位“1”是徐老师的月工资,第二个“38”的单位“1”是王老师的月工资,因为每个单位“1”表示的钱没有告诉,所以不知道一份的大小,也就无法比较两位老师捐钱的多少。
8.【答案】 B
【考点】合数与质数的特征
【解析】【解答】100以内最大的质数是97,110-97=13,13=2+11,所以聪聪11岁,得了第2名。
故答案为:B。
【分析】 满分为100分的科学知识竞赛中取得了好成绩 ,且成绩是质数,那么就想到找100以内最大的质数是97,然后用总数-成绩=名次和年龄的和,名次和年龄都是质数,也就是13分解成两个质数的和,只能是2和11,由于小学生的年龄是要大于或等于6岁的,所以只能11是年龄,2是名次。
9.【答案】 B
【考点】优化问题:方案设计问题
【解析】【解答】解:第1次:30克砝码+5克砝码,称出35克盐 ?第2次:35克盐+30克砝码,称出65克盐 ?第3次:将35克盐和65克盐放一起,变成100克盐,并再称出100克盐。还剩下100g盐,所以最小需要用天平称3次。 ?名师点评:本题难点是可以把盐和砝码放一起考虑。
故答案为:B。
【分析】 要把300克盐分成3等份,可知每一份是100g,但由于砝码只有30g和5g各一个,只用砝码是无法称出100g来,因此要利用称出来盐的重量。
10.【答案】 B
【考点】组合体的表面积,立方体的切拼
【解析】【解答】3×3×6+2×2×4+1×1×4=54+16+4=74(cm2)
故答案为:B。
【分析】正方体的表面积=棱长×棱长×6,每往上面加一个正方体,就增加了正方体的4个侧面积,加上去的正方体的上面的面积正好和被它压住的下面的面积相同,所以直接用最下面正方体的表面积+每个正方体4个侧面的面积和=图形的表面积。
三、只列式,不计算(共12分)
11.【答案】 (1)解:3×5
(2)解:(40-29)÷40
(3)解:1- 215 - 15
【考点】分数的简单应用--占总数的几分之几,异分母分数加减法
【解析】【分析】(1)长方体的占地面积就是长方体的底面积,长方体的底面积=长×宽。
(2)没有参加植树的人数=总人数-参加的人数,求一个数是另一个数的几分之几,用一个数÷另一个数。
(3)把这个菜地看作单位“1”,用1-种油菜的分率-种西红柿的分率=剩下没种的地的分率。
四、解决问题(共68分)
12.【答案】 解:( 35 + 710 )-1= 310
答:获二等奖的占获奖总人数的 310 。
【考点】分数的简单应用--占总数的几分之几,分数加减混合运算及应用
【解析】【分析】这里把获奖总人数看作单位“1”,即获得一、二、三等奖的人数看作单位“1”,把获一、二等奖的加获二、三等奖的就得到获一、二、三等奖的和获二等奖的,再把它们的和减去1,就是获二等奖的占总数的几分之几。
13.【答案】 解: 6和4的最小公倍数是12? 12÷6=2(圈)
12÷4=3(圈)
3-2=1(圈)
?答:至少12分钟后两人在起点再次相遇,此时妈妈比小亮多跑了1圈。
【考点】最小公倍数的应用
【解析】【分析】要小亮和妈妈在起点相遇,那么跑的时间要既是小亮一圈时间的倍数,又是妈妈一圈时间的倍数,也就是6和4的公倍数,要最少的时间,那就是找6和4的最小公倍数。再看12分钟里面有多少个6分钟小亮就跑多少圈,12分钟里面有多少个3分钟,妈妈就跑多少圈。
14.【答案】 解:8×8×8÷(16×5)=6.4(厘米)
答:这块钢板厚6.4厘米。
【考点】长方体的体积,正方体的体积,体积的等积变形
【解析】【分析】正方体的体积=棱长×棱长×棱长,在由正方体锻造成长方体的过程中,这个钢坯的体积不变,所以长方体的高=体积÷长÷宽。
15.【答案】 解:1.5米=15(分米)
0.18÷2=0.09(平方分米)
底面正方形边长:0.3分米
表面积:(15×0.3+15×0.3+0.3×0.3)×2=18.18(平方分米)
答:原来木料的表面积是18.18平方分米。
【考点】长方体的表面积,立方体的切拼
【解析】【分析】把长方体锯成两段后,增加的表面积就是长方体2个底面的面积,即:2个正方形的面积,这样可以求出一个底面正方形的面积,从而求出底面正方形的边长,长方体的表面积=(长×宽+长×高+宽×高)×2。
16.【答案】 (1)解:采用老师先通知1人,然后再与这个人一起给另外2个人打电话,以此类推。所以1分钟,1人得到通知;2分钟,1+2=3(人)得到通知;3分钟,3+4=7(人)得到通知;4分钟,7+8=15(人)得到通知;5分钟,15+16=31(人)得到通知;6分钟,31+32=63(人)得到通知。
答:通知所有人需要6分钟。
(2)解:8分钟可通知28-1=256-1=255(人)
答:8分钟最多能通知到255人。
【考点】时间优化问题:通知问题
【解析】【分析】用打电话的方式传递消息,最少的时间就是要充分利用知道消息的人,让他们帮忙打电话传递消息,第n分钟可以接到消息的人数是2n-1。
17.【答案】 (1)解:(150×2+250×2)×2=1600(平方米)
1600÷4=400(千克)
答:需要粉刷的外围墙(四个面)面积是1600平方米,需要400千克涂料。
(2)解:型号A:500÷25=20(元/千克)
型号B:450÷20=22.5(元/千克)
型号C:800÷40=20(元/千克)
型号C比型号A耐用比型号B便宜,所以选C。
需要400×20=8000(元)
答:需要8000元。
(3)解:(12800-8000)÷1600=3(元/平方米)
答:粉刷人工费每平方米需3元。
【考点】长方体的表面积,最佳方案:最省钱问题
【解析】【分析】(1)长方体4个侧面的面积=(长×高+宽×高)×2,1kg涂料能够刷4平方米的面积,那1600平方米里面有多少个4平方米,就需要几千克的涂料。
(2)把A、B、C三种型号涂料的单价算出来,单价=总价÷数量,再来比较单价的大小,发现A和C两种型号的涂料单价一样,但是A型号的耐用期只有2年,C型号的耐用期有5年,要便宜又耐用,因此选C,再用数量×单价=总价,算出需要的钱。
(3)用总共花的钱-涂料费用=人工费,人工费÷粉刷的面积=每平米的人工费。
18.【答案】 解:
54×4=72×3=216(厘米)
一个循环共有脚印6个,60÷6=10(个)
这条路长216×10=2160(厘米)=21.6(米)
答:这条小路长21.6米。
【考点】最小公倍数的应用
【解析】【分析】 小明每步长54厘米,爸爸每步长72厘米。两人各走完一圈后又都回到出发点,说明这条小路的长度既是54的倍数,又是72的倍数,也就是54和72的公倍数。一个最小公倍数中,爸爸和小明一共留下6个脚印,60个脚印中有几个6,就有多少个最小公倍数。
19.【答案】 解:方法一:4×6×8=192(dm3)
2.8×6×8=134.4(dm3)
投入A正方体溢出:134.4+4×4×4-192=6.4(升)
投入B正方体溢出:134.4+5×5×4-192=42.4(升)
相差:42.4-6.4=36(升)
方法二:4×4×4=64(dm3)
5×5×4=100(dm3)
100-64=36(升)
答:缸里溢出的水相差36升。
【考点】长方体的体积,正方体的体积
【解析】【分析】水的体积+正方体的体积-长方体的体积=溢出水的体积,水的体积=长方体的长×长方体的宽×水深,正方体的体积=棱长×棱长×棱长,长方体的体积=长×宽×高,分别算出放入正方体A和B溢出的水的体积,再左差即可。
20.【答案】 (1)解:
图形
①
②
③
④
……
瓷砖总块数
1
4
9
16
……
黑砖总块数
1
3
5
7
……
白砖总块数
0
1
4
9
……
(2)64;15
(3)解:第n个图形的黑砖总块数为:2n-1;第n个图形的瓷砖总块数为:n×n或n2。
【考点】数形结合规律
【解析】【解答】(2)8×8=64,2×8-1=15。
【分析】(1)看图分别数出白砖块数和黑砖块数,填入表格,瓷砖总块数=黑砖块数+白砖块数。
(2)观察表格可以知道,瓷砖总块数是等于图形序号的平方,黑砖的块数是连续的奇数,也就是图形序号的2倍再减1。
(3)根据第(2)问的观察和分析,可以知道第n个图形的黑砖总块数为:2n-1,第n个图形的瓷砖总块数为:n×n或n2。
五、挑战题(附加10分)
21.【答案】 解:2×2×6=24(平方厘米)
1×1×4=4(平方厘米)
0.5×0.5×4=1(平方厘米)
0.25×0.25×4=0.25(平方厘米)
24+4+1+0.25=29.25(平方厘米)
答:最后得到的立体图形的表面积是29.25平方厘米。
【考点】组合体的表面积,立方体的切拼
【解析】【分析】先求出原正方体的表面积,正方体的表面积=棱长×棱长×6,再求出增加的面积,每挖一个正方体,就增加该正方体的4个侧面的面积,而挖的几个正方体上、下底面多出来的面积合起来,正好与第一个大正方体挖掉的上面的面积相同,最后直接把原来正方体的表面积+每挖一个正方体增加的面积=立体图形最后的表面积。
一、填空题(共12分)(共6题;共12分)
1.把一个3平方米的花圃分成相等的4份,分别种上兰花、菊花、月季花和玫瑰花。兰花的种植面积占总面积的________,玫瑰花的种植面积是________平方米。
2.下图的秤最多能称15kg的物品。一个西瓜放在托盘上面后,仪表指针沿顺时针方向旋转90°。这个西瓜重________ kg。
3.把四块棱长2厘米的正方体粘成一个长方体,它的表面积最多会减少________平方厘米。
4.五(1)班有40多名同学,参加广播操比赛时正好排成每行8人或每行12人,且没有人员多余或不足,五(1)班有________人参加广播操比赛。
5.13×4 + 14×5 + 15×6 + 16×7 + 17×8 + 18×9 + 19×10 =________
6.大、中、小三个杯子互相倒水,用3个中杯可以把大杯倒满,用5个小杯子也能将大杯倒满。现在用中杯、小杯各往大杯中倒一次,此时大杯中的水是整个杯子的________。
二、选择题(共8分)
7.“助残日”爱心捐款活动中,徐老师捐出了月工资的 38 ,王老师也捐出了月工资的 38 。比较两位老师捐的钱,结果是(??? )。
A.?两人捐的一样多???????????????B.?徐老师捐的多???????????????C.?王老师捐的多???????????????D.?无法确定谁捐的多
8.小学生聪聪在一次满分为100分的科学知识竞赛中取得了好成绩,已知他的得分、名次及年龄均为质数,且三者之和等于110,那么聪聪得了第(??? )名。
A.?1???????????????????????????????????????????B.?2??????????????????????????????????????????C.?3???????????????????????????????????????????D.?5
9.有一架两盘天平,只有5克和30克砝码各一个,现在要把300克盐分成3等份,问最少需要用天平称(??? )次。
A.?2???????????????????????????????????????????B.?3??????????????????????????????????????????C.?4???????????????????????????????????????????D.?5
10.如图,三个棱长分别是1厘米、2厘米、3厘米的正方体叠放在一起,整个图形的表面积是(??? )平方厘米。
A.?70?????????????????????????????????????????B.?74?????????????????????????????????????????C.?78?????????????????????????????????????????D.?80
三、只列式,不计算(共12分)
11.只列式,不计算
(1)一个长方体的长、宽、高分别是5分米、3分米和2分米。如果把这个长方体放在地面上,最大的占地面积是多少平方分米?
(2)植树节到了,五(2)班40名学生有29名参加植树活动。没有参加植树活动的人数占全班学生人数的几分之几?
(3)小明家有一块 45 公顷的菜地。爸爸打算用它的 215 种油菜,用它的 15 种西红柿。还剩下这块地的几分之几没有种?
四、解决问题(共68分)
12.学校举行数学竞赛,获一、二等奖的占获奖总人数的 35 ,获二、三等奖的占获奖总人数的 710 ,获二等奖的占获奖总人数的几分之几?
13.操场跑道,小亮跑一圈要6分钟,爸爸跑一圈要3分钟,妈妈跑一圈要4分钟。如果小亮和妈妈同时起跑,至少多少分钟后两人在起点再次相遇?此时妈妈比小亮多跑了多少圈?
14.把一块棱长是8厘米的立方体钢坯,锻造成一块长16厘米,宽5厘米的长方体钢板,这块钢板有多厚?(损耗不计)
15.一根长1.5米的长方体木料,底面是正方形,把木料锯成两段后,表面积增加0.18平方分米,求原来木料的表面积。
16.放学后,老师要尽快通知全班63人第二天穿校服,如果用打电话的方式,每分钟通知1人。
(1)通知所有人至少需要多少分钟?
(2)按上面的方法,8分钟最多能通知到多少人?
17.光明学校四周的外围墙有些陈旧,现在要将四周的外围墙重新粉刷(不考虑门窗),现在不但要选购涂料,还要请粉刷工人。据了解:
(1)需要粉刷的外围墙(四个面)面积是多少平方米?需要多少千克涂料?
(2)既要便宜,又要耐用,你认为应该选哪种涂料,需要多少钱?
(3)选择(2)中的涂料,最后完成这项工程共计12800元,那么粉刷人工费每平方米需多少元?
18.夜里下了一场大雪。早上爸爸和小明一起步测小区里一条环形小路的长度,他们从同一点同向行走。小明每步长54厘米,爸爸每步长72厘米。两人各走完一圈后又都回到出发点,这时雪地上只留下60个脚印。求这条小路长。
19.一个长方体玻璃缸,尺寸如图,水深2.8dm。如果投入一个正方体铁块,投入A正方体和投入B正方体,缸里溢出的水相差多少升?
20.阅读材料:用同样规格的黑、白两色正方形瓷砖铺地,如下图。
(1)请填表:
图形
①
②
③
④
……
瓷砖总块数
1
……
黑砖总块数
1
……
白砖总块数
0
……
(2)照这样铺下去,第8个图形的瓷砖一共有________块,其中黑砖有________块。
(3)你能用含有字母的式子表示出第n个图形的黑砖总块数吗?
你能用两种不同式子表示出第n个图形的瓷砖总块数吗?
五、挑战题(附加10分)
21.下图是一个棱长为2厘米的正方体,在正方体上表面的正中,向下挖一个棱长为1厘米的正方体小洞,接着在小洞的底面正中向下挖一个棱长为 12 厘米的正方体小洞,第三个正方体小洞的挖法与前两个相同,棱长为 14 厘米,那么最后得到的立体图形的表面积是多少平方厘米?
答案解析部分
一、填空题(共12分)
1.【答案】 14;34
【考点】分数及其意义,分数与除法的关系
【解析】【解答】1÷4=14 , 3÷4=34(平方米)
故答案为:14;34。
【分析】把花圃的面积看作单位“1”,把单位“1”平均分成4份,每份占总面积的14 , 兰花的面积只有这样的一份,也就是1个14。把3平方米的花圃平均分成4份,每份的面积是34平方米,玫瑰花的面积只有这样的一份也就是1个34平方米。
2.【答案】 3.75
【考点】将简单图形平移或旋转一定的度数
【解析】【解答】360÷15=24(度),90÷24=3.75(kg)
故答案为:3.75。
【分析】圆周角是360度,被平均分成15份,一份就是24度。 仪表指针沿顺时针方向旋转90° ,90度中含有几个24度,指针就转动几格,也就是西瓜重几千克。
3.【答案】 32
【考点】立方体的切拼
【解析】【解答】2×2×8=32(平方厘米)
故答案为:32。
【分析】要使表面积减少最多,那么重合的面必须最多,因此这4块正方体应该这样摆放:, 重合的面有8个正方形,每个正方形的面积是(2×2)平方厘米。
4.【答案】 48
【考点】最小公倍数的应用
【解析】【解答】 8和12的最小公倍数为:24,24×2=48(人),40<48<50.
故答案为:48。
【分析】参加广播操比赛时正好排成每行8人或每行12人, 说明参加广播操比赛的人数是8和12的公倍数,而 五(1)班的学生有40多,所以只能是48人。
5.【答案】 730
【考点】分数的拆项,巧算分数和
【解析】【解答】原式= 13 - 14 + 14 - 15 + 15 - 16 + 16 - 17 +…+ 19 - 110 = 13 - 110 = 730
故答案为:730。
【分析】观察算式可以知道,每个分数的分母中的两个因数是相邻的自然数,并且第二个数是下一个分数分母的起始数,那么可以得到1n×(n+1)=1n-1n+1 , 可以把每个分数拆成这样的形式,再进行计算。
6.【答案】 815
【考点】最小公倍数的应用
【解析】【解答】3和5的最小公倍数是15,15÷3=5,15÷5=3,(5+3)÷15=815。
故答案为:815。
【分析】用3个中杯可以把大杯倒满,用5个小杯子也能将大杯倒满,说明大杯的容量是3和5的公倍数, 再算出中杯一次可以倒入大杯的量,小杯一次可以倒入大杯的量,最后用(中杯一次的量+小杯一次的量)÷大杯的量= 大杯中的水是整个杯子的几分之几。
二、选择题(共8分)
7.【答案】 D
【考点】单位“1”的认识及确定
【解析】【解答】因为徐老师月工资和王老师月工资分别是多少,没有告诉,所以无法比较两位老师捐钱的多少。
故答案为:D。
【分析】第一个“38”的单位“1”是徐老师的月工资,第二个“38”的单位“1”是王老师的月工资,因为每个单位“1”表示的钱没有告诉,所以不知道一份的大小,也就无法比较两位老师捐钱的多少。
8.【答案】 B
【考点】合数与质数的特征
【解析】【解答】100以内最大的质数是97,110-97=13,13=2+11,所以聪聪11岁,得了第2名。
故答案为:B。
【分析】 满分为100分的科学知识竞赛中取得了好成绩 ,且成绩是质数,那么就想到找100以内最大的质数是97,然后用总数-成绩=名次和年龄的和,名次和年龄都是质数,也就是13分解成两个质数的和,只能是2和11,由于小学生的年龄是要大于或等于6岁的,所以只能11是年龄,2是名次。
9.【答案】 B
【考点】优化问题:方案设计问题
【解析】【解答】解:第1次:30克砝码+5克砝码,称出35克盐 ?第2次:35克盐+30克砝码,称出65克盐 ?第3次:将35克盐和65克盐放一起,变成100克盐,并再称出100克盐。还剩下100g盐,所以最小需要用天平称3次。 ?名师点评:本题难点是可以把盐和砝码放一起考虑。
故答案为:B。
【分析】 要把300克盐分成3等份,可知每一份是100g,但由于砝码只有30g和5g各一个,只用砝码是无法称出100g来,因此要利用称出来盐的重量。
10.【答案】 B
【考点】组合体的表面积,立方体的切拼
【解析】【解答】3×3×6+2×2×4+1×1×4=54+16+4=74(cm2)
故答案为:B。
【分析】正方体的表面积=棱长×棱长×6,每往上面加一个正方体,就增加了正方体的4个侧面积,加上去的正方体的上面的面积正好和被它压住的下面的面积相同,所以直接用最下面正方体的表面积+每个正方体4个侧面的面积和=图形的表面积。
三、只列式,不计算(共12分)
11.【答案】 (1)解:3×5
(2)解:(40-29)÷40
(3)解:1- 215 - 15
【考点】分数的简单应用--占总数的几分之几,异分母分数加减法
【解析】【分析】(1)长方体的占地面积就是长方体的底面积,长方体的底面积=长×宽。
(2)没有参加植树的人数=总人数-参加的人数,求一个数是另一个数的几分之几,用一个数÷另一个数。
(3)把这个菜地看作单位“1”,用1-种油菜的分率-种西红柿的分率=剩下没种的地的分率。
四、解决问题(共68分)
12.【答案】 解:( 35 + 710 )-1= 310
答:获二等奖的占获奖总人数的 310 。
【考点】分数的简单应用--占总数的几分之几,分数加减混合运算及应用
【解析】【分析】这里把获奖总人数看作单位“1”,即获得一、二、三等奖的人数看作单位“1”,把获一、二等奖的加获二、三等奖的就得到获一、二、三等奖的和获二等奖的,再把它们的和减去1,就是获二等奖的占总数的几分之几。
13.【答案】 解: 6和4的最小公倍数是12? 12÷6=2(圈)
12÷4=3(圈)
3-2=1(圈)
?答:至少12分钟后两人在起点再次相遇,此时妈妈比小亮多跑了1圈。
【考点】最小公倍数的应用
【解析】【分析】要小亮和妈妈在起点相遇,那么跑的时间要既是小亮一圈时间的倍数,又是妈妈一圈时间的倍数,也就是6和4的公倍数,要最少的时间,那就是找6和4的最小公倍数。再看12分钟里面有多少个6分钟小亮就跑多少圈,12分钟里面有多少个3分钟,妈妈就跑多少圈。
14.【答案】 解:8×8×8÷(16×5)=6.4(厘米)
答:这块钢板厚6.4厘米。
【考点】长方体的体积,正方体的体积,体积的等积变形
【解析】【分析】正方体的体积=棱长×棱长×棱长,在由正方体锻造成长方体的过程中,这个钢坯的体积不变,所以长方体的高=体积÷长÷宽。
15.【答案】 解:1.5米=15(分米)
0.18÷2=0.09(平方分米)
底面正方形边长:0.3分米
表面积:(15×0.3+15×0.3+0.3×0.3)×2=18.18(平方分米)
答:原来木料的表面积是18.18平方分米。
【考点】长方体的表面积,立方体的切拼
【解析】【分析】把长方体锯成两段后,增加的表面积就是长方体2个底面的面积,即:2个正方形的面积,这样可以求出一个底面正方形的面积,从而求出底面正方形的边长,长方体的表面积=(长×宽+长×高+宽×高)×2。
16.【答案】 (1)解:采用老师先通知1人,然后再与这个人一起给另外2个人打电话,以此类推。所以1分钟,1人得到通知;2分钟,1+2=3(人)得到通知;3分钟,3+4=7(人)得到通知;4分钟,7+8=15(人)得到通知;5分钟,15+16=31(人)得到通知;6分钟,31+32=63(人)得到通知。
答:通知所有人需要6分钟。
(2)解:8分钟可通知28-1=256-1=255(人)
答:8分钟最多能通知到255人。
【考点】时间优化问题:通知问题
【解析】【分析】用打电话的方式传递消息,最少的时间就是要充分利用知道消息的人,让他们帮忙打电话传递消息,第n分钟可以接到消息的人数是2n-1。
17.【答案】 (1)解:(150×2+250×2)×2=1600(平方米)
1600÷4=400(千克)
答:需要粉刷的外围墙(四个面)面积是1600平方米,需要400千克涂料。
(2)解:型号A:500÷25=20(元/千克)
型号B:450÷20=22.5(元/千克)
型号C:800÷40=20(元/千克)
型号C比型号A耐用比型号B便宜,所以选C。
需要400×20=8000(元)
答:需要8000元。
(3)解:(12800-8000)÷1600=3(元/平方米)
答:粉刷人工费每平方米需3元。
【考点】长方体的表面积,最佳方案:最省钱问题
【解析】【分析】(1)长方体4个侧面的面积=(长×高+宽×高)×2,1kg涂料能够刷4平方米的面积,那1600平方米里面有多少个4平方米,就需要几千克的涂料。
(2)把A、B、C三种型号涂料的单价算出来,单价=总价÷数量,再来比较单价的大小,发现A和C两种型号的涂料单价一样,但是A型号的耐用期只有2年,C型号的耐用期有5年,要便宜又耐用,因此选C,再用数量×单价=总价,算出需要的钱。
(3)用总共花的钱-涂料费用=人工费,人工费÷粉刷的面积=每平米的人工费。
18.【答案】 解:
54×4=72×3=216(厘米)
一个循环共有脚印6个,60÷6=10(个)
这条路长216×10=2160(厘米)=21.6(米)
答:这条小路长21.6米。
【考点】最小公倍数的应用
【解析】【分析】 小明每步长54厘米,爸爸每步长72厘米。两人各走完一圈后又都回到出发点,说明这条小路的长度既是54的倍数,又是72的倍数,也就是54和72的公倍数。一个最小公倍数中,爸爸和小明一共留下6个脚印,60个脚印中有几个6,就有多少个最小公倍数。
19.【答案】 解:方法一:4×6×8=192(dm3)
2.8×6×8=134.4(dm3)
投入A正方体溢出:134.4+4×4×4-192=6.4(升)
投入B正方体溢出:134.4+5×5×4-192=42.4(升)
相差:42.4-6.4=36(升)
方法二:4×4×4=64(dm3)
5×5×4=100(dm3)
100-64=36(升)
答:缸里溢出的水相差36升。
【考点】长方体的体积,正方体的体积
【解析】【分析】水的体积+正方体的体积-长方体的体积=溢出水的体积,水的体积=长方体的长×长方体的宽×水深,正方体的体积=棱长×棱长×棱长,长方体的体积=长×宽×高,分别算出放入正方体A和B溢出的水的体积,再左差即可。
20.【答案】 (1)解:
图形
①
②
③
④
……
瓷砖总块数
1
4
9
16
……
黑砖总块数
1
3
5
7
……
白砖总块数
0
1
4
9
……
(2)64;15
(3)解:第n个图形的黑砖总块数为:2n-1;第n个图形的瓷砖总块数为:n×n或n2。
【考点】数形结合规律
【解析】【解答】(2)8×8=64,2×8-1=15。
【分析】(1)看图分别数出白砖块数和黑砖块数,填入表格,瓷砖总块数=黑砖块数+白砖块数。
(2)观察表格可以知道,瓷砖总块数是等于图形序号的平方,黑砖的块数是连续的奇数,也就是图形序号的2倍再减1。
(3)根据第(2)问的观察和分析,可以知道第n个图形的黑砖总块数为:2n-1,第n个图形的瓷砖总块数为:n×n或n2。
五、挑战题(附加10分)
21.【答案】 解:2×2×6=24(平方厘米)
1×1×4=4(平方厘米)
0.5×0.5×4=1(平方厘米)
0.25×0.25×4=0.25(平方厘米)
24+4+1+0.25=29.25(平方厘米)
答:最后得到的立体图形的表面积是29.25平方厘米。
【考点】组合体的表面积,立方体的切拼
【解析】【分析】先求出原正方体的表面积,正方体的表面积=棱长×棱长×6,再求出增加的面积,每挖一个正方体,就增加该正方体的4个侧面的面积,而挖的几个正方体上、下底面多出来的面积合起来,正好与第一个大正方体挖掉的上面的面积相同,最后直接把原来正方体的表面积+每挖一个正方体增加的面积=立体图形最后的表面积。
