人教版数学四年级上册:第5单元 平行四边形和梯形 课件(共49张PPT)
文档属性
| 名称 | 人教版数学四年级上册:第5单元 平行四边形和梯形 课件(共49张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-22 00:00:00 | ||
图片预览

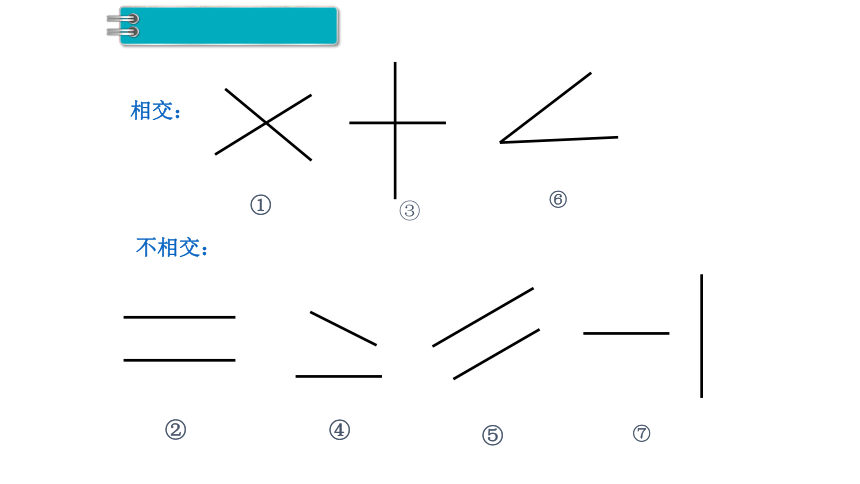





文档简介
(共49张PPT)
四年级数学上册(RJ) 教学课件
第 1 课时 平 行 与 垂 直
第 5 单元 平行四边形和梯形
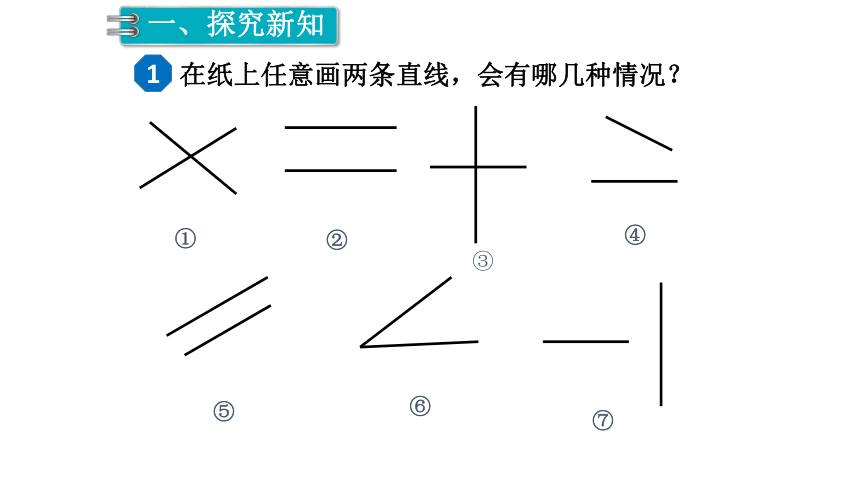
①
②
④
⑤
③
⑥
⑦
在纸上任意画两条直线,会有哪几种情况?
一、探究新知
1
相交:
不相交:
①
③
⑥
②
④
⑤
⑦
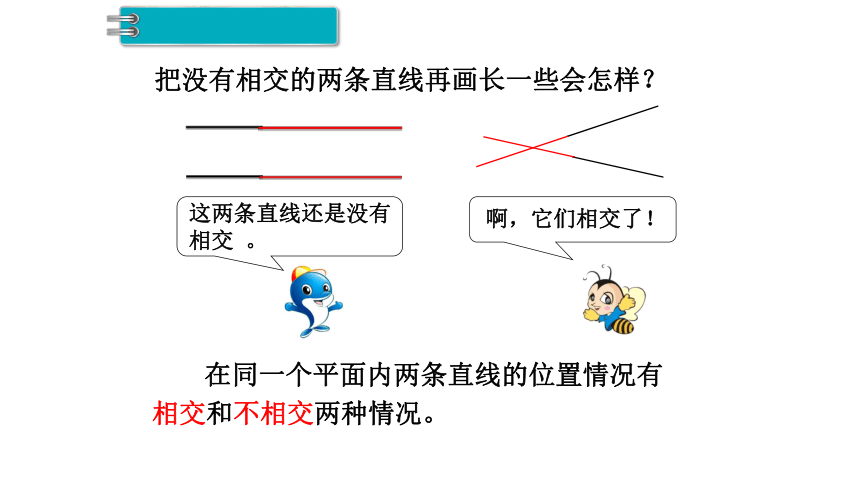
把没有相交的两条直线再画长一些会怎样?
在同一个平面内两条直线的位置情况有
相交和不相交两种情况。
这两条直线还是没有相交 。
啊,它们相交了!
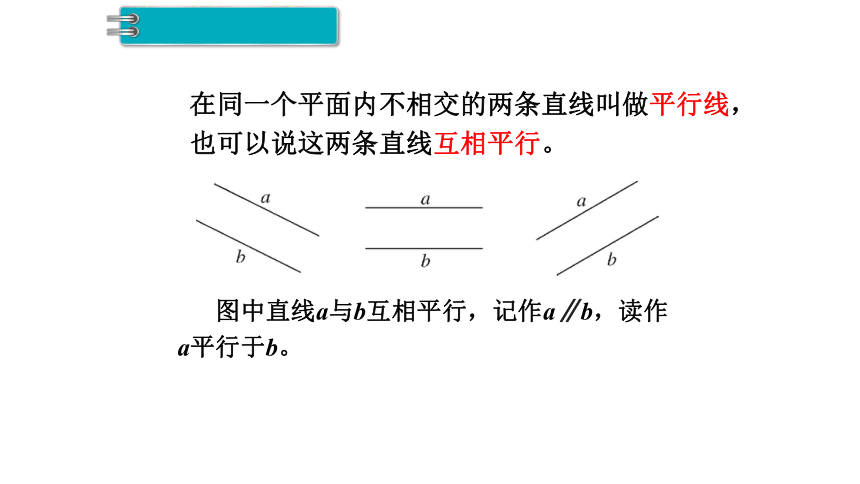
在同一个平面内不相交的两条直线叫做平行线,
也可以说这两条直线互相平行。
图中直线a与b互相平行,记作a∥b,读作a平行于b。
日常生活中的平行线。
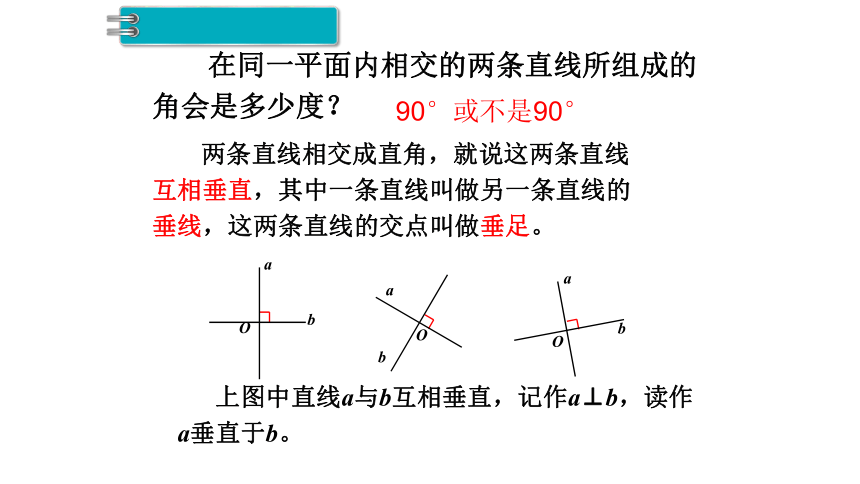
两条直线相交成直角,就说这两条直线
互相垂直,其中一条直线叫做另一条直线的
垂线,这两条直线的交点叫做垂足。
O
a
b
O
a
b
O
a
b
上图中直线a与b互相垂直,记作a⊥b,读作
a垂直于b。
在同一平面内相交的两条直线所组成的
角会是多少度?
90°或不是90°
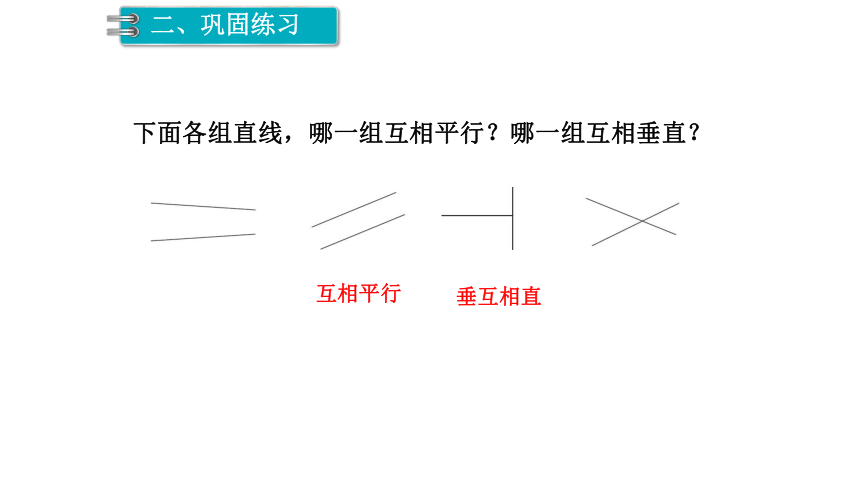
下面各组直线,哪一组互相平行?哪一组互相垂直?
互相平行
垂互相直
二、巩固练习
把两根小棒都摆成和第三根小棒互相平行。
a
b
c
(2)问题:你摆的和他一样吗?摆完后你有
什么发现?
(1)问题:你能将两根小棒都摆成和第三根
小棒互相平行吗?
(3)问题:你发现这个规律了吗?能再说一
说吗?
a
b
c
把两根小棒都摆成和第三根小棒互相垂直。
(1)要求:请你将两根小棒都摆成和第三根
小棒互相垂直。
(2)问题:你是怎么摆的?
(3)学生汇报。
(4)问题:观察这三根小棒,你有什么发现?
将你的发现和同学说一说。
三、课堂小结
在同一平面内,两条直线的位置关系有相交和不相交,不相交的两条直线叫做平行线,也可以说这两条直线互相平行。
相交的两条直线的关系有垂直和不垂直,如果两条直线互相垂直,其中一条直线叫做另一条直线的垂线,这两条直线的交点叫做垂足。
四、拓展训练
选一选。
1.在同一平面内的两条直线,一定是( )。
A、相交的 B、平行的 C、不相交就平行
2.两条直线相交,如果其中一个角是直角,那么这两条直线( )。
A、互相垂直 B、互相平行 C、无法确定
3.在同一平面内,有两条直线都与同一条直线平行,这两条直线( )。
A、互相垂直 B、互相平行 C、相交
4.长方形相邻的两条边( ),相对的两条边( )。
A、互相平行 B、互相垂直 C、没有关系
C
A
B
B
A
四年级数学上册(RJ) 教学课件
第 2 课时 画 垂 线
第 5 单元 平行四边形和梯形
一、创设情境
1.提问:什么叫做垂线?
2.举例说一说生活中的垂线。
3.怎样画垂线呢?
如果两条直线相交成直角,就说这两条直线互相垂直,其中一条直线叫做另一条直线的垂线。
二、自主探究
1.过直线上一点画这条直线的垂线。
垂足
(1)把三角尺的一条直角边与已知直线重合。
(2)沿着已知直线移动三角尺,使三角尺的直角
顶点与直线上的已知点重合。
(3)沿另一条直角边画一条经过已知点的直线,
所画直线与已知直线互相垂直。
2
2.过直线外一点画这条直线的垂线,用三角尺
应该怎样画呢?试一试。
说一说是怎么画的。
(1)从直线外一点A,到这条直线画几条线段。
量一量所画线段的长度,哪一条最短?
的线段最短。
A
结论:从直线外一点到这条直线所画的垂直线段
最短,它的长度叫做这点到直线的距离。
垂直
3
(2)下图中,a∥b。在a上任选几个点,分别向b
画垂直的线段。量一量这些线段的长度,
你发现了什么?
a
b
端点分别在两条平行线上,且与平行线
垂直的所有线段的长度都 。
相等
1.右图中,小明如果从 A点过马
路,怎样走路线最短?为什么?
把最短的路线画出来。
A
2.请用在例3中发现的规律,检验下面各组直线
a、b是否互相平行。
三、巩固练习
四、课堂小结
画垂线有两个重合:一是三角尺的一条直角边与已知直线重合,二是点在直线上时,三角尺的顶点与这一点重合,点在直线外时,三角尺的另一条直线边经过这一点。
从直线外一点到这条直线所画的线段中垂直线段最短,它的长度叫做这点到直线的距离。
利用两条平行线间与两条平行线相互垂直的线段长度相等的性质,可以检验两条直线是否互相平行。
五、拓展训练
判断题。(对的打"√",错的打"×")
1.在同一平面内不相交的两条直线叫做平行线。 ( )
2.两条平行线之间只能作一条垂线。 ( )
3.平面内两条直线不垂直就一定平行。 ( )
4.两条平行线间的距离处处相等。 ( )
√
×
×
√
四年级数学上册(RJ) 教学课件
第 3 课时 画 长 方 形
第 5 单元 平行四边形和梯形
一、创设情境
提问:
1.怎样过直线上一点画这条直线的垂线,如果
这一点不在直线上,又怎样画呢?
2.怎样过直线外一点画这条直线的平行线?
3.什么叫做点到直线的距离?平行线间的垂直
线段有什么关系?
长方形中,哪些线段是互相平行的?哪些线段
是互相垂直的?
怎样画一个长方形呢?因为长方形的对边互相
平行,相邻的两条边互相垂直,我们可不可以用画
垂线的方法来画呢?
二、自主探究
画一个长10厘米、宽8厘米的长方形。
阅读与理解
知道长方形的 、 ,要画出这个长方形。
长
宽
2
1.画一条长10厘米的线段。
2.分别过线段的两个端点在同一侧画两条与线段
互相垂直的8厘米线段。
3.把两条垂线的另一个端点连接起来。
分析与画图
回顾与反思
你是怎样画出这
个长方形的?
先画出长方形的
长,再……
1.画一个长4厘米,
宽3厘米的长方形。
2.画一个边长5厘米
的正方形。
3.要从幸福镇修一条通往公路的水泥路。
怎样修路最近呢?
三、巩固练习
判断题。
1.知道长方形的长和宽就可以画长方形。 ( )
2.两条直线相交时,这两条直线互相垂直。 ( )
√
×
四、课堂小结
画长方形的方法:先画一条线段作长方形的长,再从画出的线段两端画两条与这条线段垂直的线段,使画出的两条线段长度相等,最后把所画的两条线段另外的端点连起来。
五、拓展训练
在下图中,请你找出能与线段AB组成长方形的线段。
A
B
C
D
E
F
G
H
A
B
C
D
E
F
G
H
如图,与线段AB组成长方形的线段有CD,HF,EG
四年级数学上册(RJ) 教学课件
第 4 课时 平 行 四 边 形 的 认 识
第 5 单元 平行四边形和梯形
一、创设情境,引入新课
上面图中都有平行四边形。
1
二、自主探究
(1)平行四边形有什么特点?
平行四边形的对边
互相平行。
对边也相等。
两组对边分别平行的四边形,叫做
平行四边形。
(2)认识平行四边形各部分的名称。
从平行四边形一条边上的
一点向对边引一条垂线,这点
和垂足之间的线段叫做平行四
边形的高,垂足所在的边叫做
平行四边形的底。
1. 对于平行四边形你还有哪些了解?
2. 什么是平行四边形的底和高呢?
底
高
下面哪些图形是平行四边形?画出每个平行四边形的高。
平行四边形
平行四边形
平行四边形
三、巩固练习
(1)用四根吸管串成一个长方形,然后用两手捏住
长方形的两个对角,向相反方向拉。
两组对边有什么变化?
拉成了什么图形?
拉成了不同的平行
四边形。
2
通过动手操作,我们发现平行四边形容易
变形。平行四边形的这种特点,在实际生活中
有广泛的应用。
伸缩门
升降机
你还见过应用平行四边形这一特性的事例吗?
1.用四根小棒摆一个平行四边形。
平行四边形的四条边确定了,它的形状能确定吗?
不能确定
这四根小棒能围成不同
的平行四边形吗?
能
巩固练习
2. 在点子图上画出两个不同的平行四边形。
分别画出它们的高并量出来。
四、课堂小结
从平行四边形一条边上的一点到对边引一条垂线,这点和垂足之间的线段叫做平行四边形的高,垂足所在的边叫做平行四边形的底。
平行四边形的特征:两组对边分别平行且相等。
五、拓展训练
判一判。
1.平行四边形一定能分成两个完全一样的梯形。 ( )
2.梯形的底和高一定是垂直的。 ( )
3.三角形具有稳定性的特点,而平行四边形却有容易变形的特点。
( )
4.梯形是只有一组对边平行的四边形。 ( )
√
√
√
√
四年级数学上册(RJ) 教学课件
第 5 课时 梯 形 的 认 识
第 5 单元 平行四边形和梯形
你见过下面这样的图形吗?它们有什么共同点?
只有一组对边平行的四边形叫做梯形。
一、学习新知
3
认识梯形各部分名称。
上底
下底
腰
腰
高
平行的两条边分别叫做梯形的上底和下底。
通过上底一个顶点向对边(下底)引垂线,
这点和垂足之间的线段叫做梯形的高。
认识两种特殊的梯形。
两腰相等的梯形叫做等腰梯形。
有一个角是直角的梯形叫做直角梯形。
等腰梯形
直角梯形
下面哪些图形是梯形?画出每个梯形的高,分别指出它们的上底、下底和腰。
梯形
梯形
梯形
上底
下底
腰
上底
上
底
下
底
下底
腰
腰
腰
腰
腰
二、巩固练习
三、课堂小结
1.只有一组对边互相平行的四边形叫做梯形。
2.梯形的高是从上底的一个点向下底所作的垂直线段。平行四边形能作两种长度的高,梯形只有一种长度的高。
四、拓展训练
选一选。
1.把一个长方形框架拉成一个平行四边形,这个平行四边形的周长比原长方形的周长( )。
A、大 B、小 C、一样大 D、无法比较
2.从直线外一点到这条直线的距离,是指这一点到这条直线的( )的长。
A、线段 B、射线 C、直线 D、垂直线段
3.在一个等腰梯形中画一条线段,可以将它分割成两个完全一样的( )。
A、梯形 B、平行四边形 C、三角形
C
D
C
四年级数学上册(RJ) 教学课件
第 1 课时 平 行 与 垂 直
第 5 单元 平行四边形和梯形
①
②
④
⑤
③
⑥
⑦
在纸上任意画两条直线,会有哪几种情况?
一、探究新知
1
相交:
不相交:
①
③
⑥
②
④
⑤
⑦
把没有相交的两条直线再画长一些会怎样?
在同一个平面内两条直线的位置情况有
相交和不相交两种情况。
这两条直线还是没有相交 。
啊,它们相交了!
在同一个平面内不相交的两条直线叫做平行线,
也可以说这两条直线互相平行。
图中直线a与b互相平行,记作a∥b,读作a平行于b。
日常生活中的平行线。
两条直线相交成直角,就说这两条直线
互相垂直,其中一条直线叫做另一条直线的
垂线,这两条直线的交点叫做垂足。
O
a
b
O
a
b
O
a
b
上图中直线a与b互相垂直,记作a⊥b,读作
a垂直于b。
在同一平面内相交的两条直线所组成的
角会是多少度?
90°或不是90°
下面各组直线,哪一组互相平行?哪一组互相垂直?
互相平行
垂互相直
二、巩固练习
把两根小棒都摆成和第三根小棒互相平行。
a
b
c
(2)问题:你摆的和他一样吗?摆完后你有
什么发现?
(1)问题:你能将两根小棒都摆成和第三根
小棒互相平行吗?
(3)问题:你发现这个规律了吗?能再说一
说吗?
a
b
c
把两根小棒都摆成和第三根小棒互相垂直。
(1)要求:请你将两根小棒都摆成和第三根
小棒互相垂直。
(2)问题:你是怎么摆的?
(3)学生汇报。
(4)问题:观察这三根小棒,你有什么发现?
将你的发现和同学说一说。
三、课堂小结
在同一平面内,两条直线的位置关系有相交和不相交,不相交的两条直线叫做平行线,也可以说这两条直线互相平行。
相交的两条直线的关系有垂直和不垂直,如果两条直线互相垂直,其中一条直线叫做另一条直线的垂线,这两条直线的交点叫做垂足。
四、拓展训练
选一选。
1.在同一平面内的两条直线,一定是( )。
A、相交的 B、平行的 C、不相交就平行
2.两条直线相交,如果其中一个角是直角,那么这两条直线( )。
A、互相垂直 B、互相平行 C、无法确定
3.在同一平面内,有两条直线都与同一条直线平行,这两条直线( )。
A、互相垂直 B、互相平行 C、相交
4.长方形相邻的两条边( ),相对的两条边( )。
A、互相平行 B、互相垂直 C、没有关系
C
A
B
B
A
四年级数学上册(RJ) 教学课件
第 2 课时 画 垂 线
第 5 单元 平行四边形和梯形
一、创设情境
1.提问:什么叫做垂线?
2.举例说一说生活中的垂线。
3.怎样画垂线呢?
如果两条直线相交成直角,就说这两条直线互相垂直,其中一条直线叫做另一条直线的垂线。
二、自主探究
1.过直线上一点画这条直线的垂线。
垂足
(1)把三角尺的一条直角边与已知直线重合。
(2)沿着已知直线移动三角尺,使三角尺的直角
顶点与直线上的已知点重合。
(3)沿另一条直角边画一条经过已知点的直线,
所画直线与已知直线互相垂直。
2
2.过直线外一点画这条直线的垂线,用三角尺
应该怎样画呢?试一试。
说一说是怎么画的。
(1)从直线外一点A,到这条直线画几条线段。
量一量所画线段的长度,哪一条最短?
的线段最短。
A
结论:从直线外一点到这条直线所画的垂直线段
最短,它的长度叫做这点到直线的距离。
垂直
3
(2)下图中,a∥b。在a上任选几个点,分别向b
画垂直的线段。量一量这些线段的长度,
你发现了什么?
a
b
端点分别在两条平行线上,且与平行线
垂直的所有线段的长度都 。
相等
1.右图中,小明如果从 A点过马
路,怎样走路线最短?为什么?
把最短的路线画出来。
A
2.请用在例3中发现的规律,检验下面各组直线
a、b是否互相平行。
三、巩固练习
四、课堂小结
画垂线有两个重合:一是三角尺的一条直角边与已知直线重合,二是点在直线上时,三角尺的顶点与这一点重合,点在直线外时,三角尺的另一条直线边经过这一点。
从直线外一点到这条直线所画的线段中垂直线段最短,它的长度叫做这点到直线的距离。
利用两条平行线间与两条平行线相互垂直的线段长度相等的性质,可以检验两条直线是否互相平行。
五、拓展训练
判断题。(对的打"√",错的打"×")
1.在同一平面内不相交的两条直线叫做平行线。 ( )
2.两条平行线之间只能作一条垂线。 ( )
3.平面内两条直线不垂直就一定平行。 ( )
4.两条平行线间的距离处处相等。 ( )
√
×
×
√
四年级数学上册(RJ) 教学课件
第 3 课时 画 长 方 形
第 5 单元 平行四边形和梯形
一、创设情境
提问:
1.怎样过直线上一点画这条直线的垂线,如果
这一点不在直线上,又怎样画呢?
2.怎样过直线外一点画这条直线的平行线?
3.什么叫做点到直线的距离?平行线间的垂直
线段有什么关系?
长方形中,哪些线段是互相平行的?哪些线段
是互相垂直的?
怎样画一个长方形呢?因为长方形的对边互相
平行,相邻的两条边互相垂直,我们可不可以用画
垂线的方法来画呢?
二、自主探究
画一个长10厘米、宽8厘米的长方形。
阅读与理解
知道长方形的 、 ,要画出这个长方形。
长
宽
2
1.画一条长10厘米的线段。
2.分别过线段的两个端点在同一侧画两条与线段
互相垂直的8厘米线段。
3.把两条垂线的另一个端点连接起来。
分析与画图
回顾与反思
你是怎样画出这
个长方形的?
先画出长方形的
长,再……
1.画一个长4厘米,
宽3厘米的长方形。
2.画一个边长5厘米
的正方形。
3.要从幸福镇修一条通往公路的水泥路。
怎样修路最近呢?
三、巩固练习
判断题。
1.知道长方形的长和宽就可以画长方形。 ( )
2.两条直线相交时,这两条直线互相垂直。 ( )
√
×
四、课堂小结
画长方形的方法:先画一条线段作长方形的长,再从画出的线段两端画两条与这条线段垂直的线段,使画出的两条线段长度相等,最后把所画的两条线段另外的端点连起来。
五、拓展训练
在下图中,请你找出能与线段AB组成长方形的线段。
A
B
C
D
E
F
G
H
A
B
C
D
E
F
G
H
如图,与线段AB组成长方形的线段有CD,HF,EG
四年级数学上册(RJ) 教学课件
第 4 课时 平 行 四 边 形 的 认 识
第 5 单元 平行四边形和梯形
一、创设情境,引入新课
上面图中都有平行四边形。
1
二、自主探究
(1)平行四边形有什么特点?
平行四边形的对边
互相平行。
对边也相等。
两组对边分别平行的四边形,叫做
平行四边形。
(2)认识平行四边形各部分的名称。
从平行四边形一条边上的
一点向对边引一条垂线,这点
和垂足之间的线段叫做平行四
边形的高,垂足所在的边叫做
平行四边形的底。
1. 对于平行四边形你还有哪些了解?
2. 什么是平行四边形的底和高呢?
底
高
下面哪些图形是平行四边形?画出每个平行四边形的高。
平行四边形
平行四边形
平行四边形
三、巩固练习
(1)用四根吸管串成一个长方形,然后用两手捏住
长方形的两个对角,向相反方向拉。
两组对边有什么变化?
拉成了什么图形?
拉成了不同的平行
四边形。
2
通过动手操作,我们发现平行四边形容易
变形。平行四边形的这种特点,在实际生活中
有广泛的应用。
伸缩门
升降机
你还见过应用平行四边形这一特性的事例吗?
1.用四根小棒摆一个平行四边形。
平行四边形的四条边确定了,它的形状能确定吗?
不能确定
这四根小棒能围成不同
的平行四边形吗?
能
巩固练习
2. 在点子图上画出两个不同的平行四边形。
分别画出它们的高并量出来。
四、课堂小结
从平行四边形一条边上的一点到对边引一条垂线,这点和垂足之间的线段叫做平行四边形的高,垂足所在的边叫做平行四边形的底。
平行四边形的特征:两组对边分别平行且相等。
五、拓展训练
判一判。
1.平行四边形一定能分成两个完全一样的梯形。 ( )
2.梯形的底和高一定是垂直的。 ( )
3.三角形具有稳定性的特点,而平行四边形却有容易变形的特点。
( )
4.梯形是只有一组对边平行的四边形。 ( )
√
√
√
√
四年级数学上册(RJ) 教学课件
第 5 课时 梯 形 的 认 识
第 5 单元 平行四边形和梯形
你见过下面这样的图形吗?它们有什么共同点?
只有一组对边平行的四边形叫做梯形。
一、学习新知
3
认识梯形各部分名称。
上底
下底
腰
腰
高
平行的两条边分别叫做梯形的上底和下底。
通过上底一个顶点向对边(下底)引垂线,
这点和垂足之间的线段叫做梯形的高。
认识两种特殊的梯形。
两腰相等的梯形叫做等腰梯形。
有一个角是直角的梯形叫做直角梯形。
等腰梯形
直角梯形
下面哪些图形是梯形?画出每个梯形的高,分别指出它们的上底、下底和腰。
梯形
梯形
梯形
上底
下底
腰
上底
上
底
下
底
下底
腰
腰
腰
腰
腰
二、巩固练习
三、课堂小结
1.只有一组对边互相平行的四边形叫做梯形。
2.梯形的高是从上底的一个点向下底所作的垂直线段。平行四边形能作两种长度的高,梯形只有一种长度的高。
四、拓展训练
选一选。
1.把一个长方形框架拉成一个平行四边形,这个平行四边形的周长比原长方形的周长( )。
A、大 B、小 C、一样大 D、无法比较
2.从直线外一点到这条直线的距离,是指这一点到这条直线的( )的长。
A、线段 B、射线 C、直线 D、垂直线段
3.在一个等腰梯形中画一条线段,可以将它分割成两个完全一样的( )。
A、梯形 B、平行四边形 C、三角形
C
D
C
