人教版数学六年级上册:第4单元 比 课件(共39张PPT)
文档属性
| 名称 | 人教版数学六年级上册:第4单元 比 课件(共39张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 812.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-23 16:25:30 | ||
图片预览









文档简介
六年级数学上册(RJ) 教学课件
第 1 课时 比 的 意 义
第 4 单元 比
2003年10月15日,我国第一艘载人飞船“神舟”五号顺利升空。在太空中,执行此次任务的航天员杨利伟在飞船里向人们展示了联合国旗和中华人民共和国国旗。
一、创设情境,引入新课
一、创设情境,引入新课
提问:
(1)图上画了些什么?你了解到了哪些信息?有何感想?
(2)根据画面情境,你想提出什么问题?
(3)杨利伟在载人飞船上向人们展示的两面国旗的长和宽是多少?你是怎样用算式表示它们的关系的?
杨利伟展示的两面旗都是长15cm,宽10cm。怎样用算式表示它们长和宽倍数的关系?
一、创设情境,引入新课
可以用“15÷10”表
示长是宽的多少倍。
也可以用“10÷15”表
示宽是长的几分之几。
有时我们也把这两个数量之间的关系说成:
长和宽的比是15比10,宽和长的比是10比15.
一、创设情境,引入新课
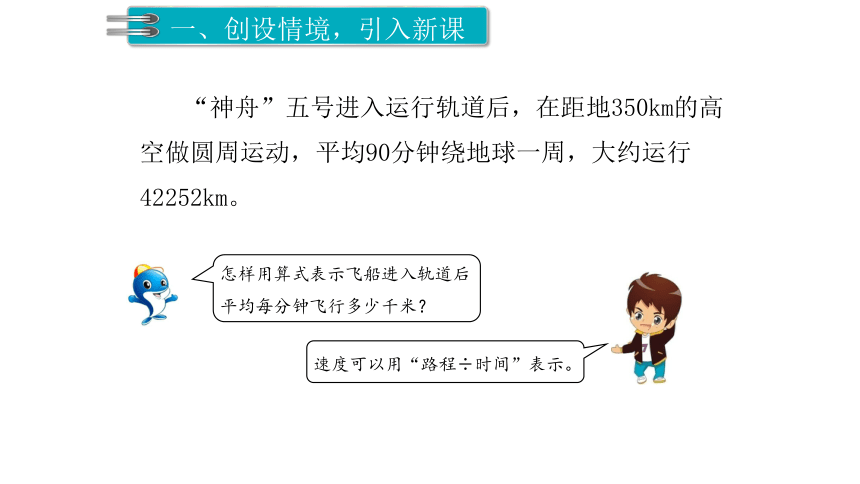
“神舟”五号进入运行轨道后,在距地350km的高空做圆周运动,平均90分钟绕地球一周,大约运行42252km。
怎样用算式表示飞船进入轨道后
平均每分钟飞行多少千米?
速度可以用“路程÷时间”表示。
二、探究新知
我们也可以用比来表示路程和时间的关系:
路程和时间的比是42252比90。
两个数的比表示两个数相除。
15比10记作15∶10
10比15记作10∶15
42252比90记作42252∶90
“∶”是比号。
二、探究新知
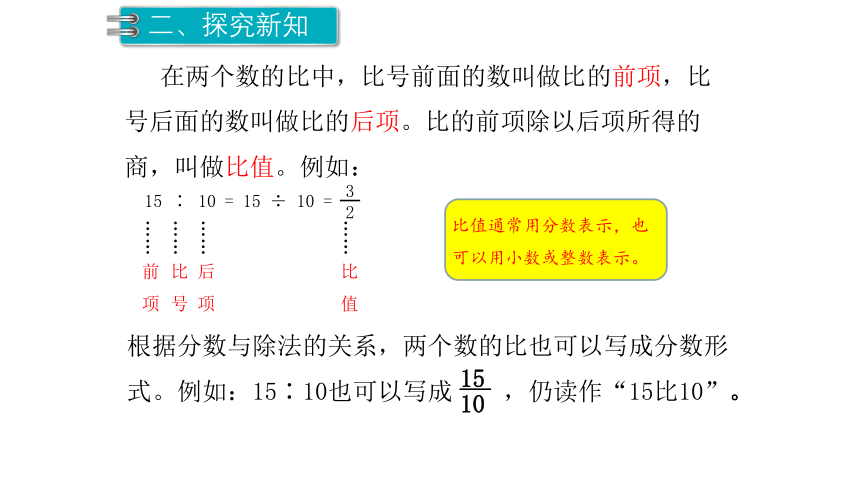
在两个数的比中,比号前面的数叫做比的前项,比号后面的数叫做比的后项。比的前项除以后项所得的商,叫做比值。例如:
3
2
15 ∶ 10 = 15 ÷ 10 =
……
前
项
……
比号
……
后项
……
比值
比值通常用分数表示,也可以用小数或整数表示。
根据分数与除法的关系,两个数的比也可以写成分数形式。例如:15∶10也可以写成 ,仍读作“15比10”。
15
10
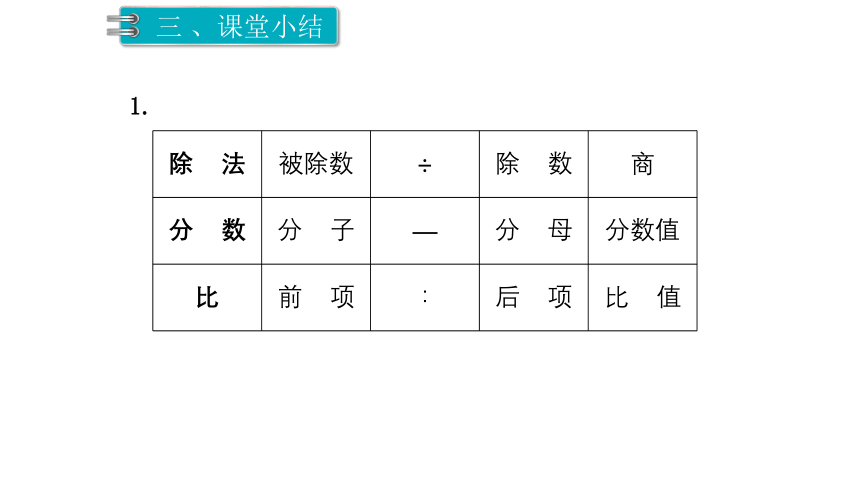
除 法
被除数
÷
除 数
商
分 数
分 子
—
分 母
分数值
比
前 项
∶
后 项
比 值
1.
三 、课堂小结
2.
比与分数、除法的内在联系十分紧密,但又有区别。除法是一种运算,分数是一种数,比是表示两个数之间的关系,它们各有不同的意义。所以在说它们之间关系的时候,要说“相当于”,而不能说“等于”或“是”。
三、课堂小结
1.小敏和小亮在文具店买同样的练习本。小敏买了6本,共花了1.8元。小亮买了8本,共花了2.4元。
小敏和小亮买的练习本数之比是( )∶( ),比值是( );
花的钱数之比是( )∶( ),比值是( )。
2. 3∶( )=24 ( )∶8=0.5
1
8
6
8
0.75
1.8
2.4
0.75
4
四、巩固练习
3.你还记得商不变的规律和分数的基本性质吗?
被除数和除数同时乘或除以相同的数……
分数的分子和分母同时乘或除以相同的数……
商不变的规律:被除数和除数同时乘或除以相同的数(0除外),商不变。
分数的基本性质:分数的分子和分母同时乘或除以相同的数(0除外),分数的大小不变。
四、巩固练习
四、巩固练习
六年级(5)班有男生20人,女生18人,求下列各比。
(1) 男生人数∶女生人数;
(2) 女生人数∶全班人数;
(3) 男生人数∶全班人数。
(1) 10 ∶9 (2)9∶19
(3)10 ∶19
六年级数学上册(RJ) 教学课件
第 2 课时 比 的 基 本 性 质
第 4 单元 比
一、复习导入
小明、小强、小丽都喜欢制作折纸。有一天,他们三人在争论谁每分钟折的纸鹤数多?
小明说:“我八分钟折了六只。”
小强说:“我四分钟折了三只。”
小丽说:“我十六分钟折了十二只。”
问题:小明、小强和小丽折的只数和时间(分)的比是多少?
小明6∶8 小强3∶4 小丽12∶16
谁折的速度快呢?
联系比和除法、分数的关系,想一想:在比中有什么样的规律?
二、探究新知
先利用比和除法的关系来研究。
6∶8=6÷8= =
6
8
3
4
12∶16=12÷16= =
12
16
3
4
6∶8=(6×2)÷(8×2)=12÷16
6∶8=(6×2)∶(8×2)=12∶16
6∶8=(6÷2)∶(8÷2)=3∶4
6÷8=(6÷2)÷(8÷2)=3÷4
二、探究新知
你能根据比和分数的关系研究比中的规律吗?
比的前项和后项同时乘或除以相同的数(0除外),比值不变。这叫做比的基本性质。
根据比的基本性质,可以把比化成最简单的整数比。
二、探究新知
(1)“神舟”五号搭载了两面联合国旗,一面长15cm,宽10cm(前面展示过),另一面长180cm,宽120cm(如图)。
1
15cm
10cm
180cm
120cm
这两面联合国旗长和宽的最简单的整数比分别是多少?
15∶10 =(15÷5)∶(10÷5)
= 3∶2
180∶120 =(180÷ )∶(120÷ )
=( )∶( )
想:5是15和10的什么数?为什么要除以5?
60
60
3
2
二、探究新知
(2)把下面各比化成最简单的整数比。
想:为什么要乘18?
0.75∶2=(0.75×100)∶(2×100)
= 75∶200
=( )∶( )
∶ =( ×18)∶( ×18)
=( )∶( )
1
6
2
9
∶
0.75∶2
1
6
2
9
1
6
2
9
3
4
3
8
二、探究新知
当一个比的前项或后项不是整数时,怎样把它化成最简单的整数比?
分数比的化简方法:(1)比的前项和后项同时乘它们分母的最小公倍数,转化成整数比,再进行化简。(2)利用求比值的方法也可以化简分数比,但结果必须写成比的形式。
小数比的化简方法:先把比的前项和后项的小数点同时向右移动相同的位数,转化成整数比,再按照整数比的化简方法进行化简。
二、探究新知
二、探究新知
介绍黄金比:
问题:1. 你听说过“黄金比”吗?
4. 你还了解生活中的黄金比吗?课下查阅相关的资料。
把一条线段分成两部分,如果较短部分与较长部分长度之比等于较长部分与整体长度之比,我们把这个比称为黄金比(约为 0.618︰1)。当一个物体的两个部分长度的比大致符合黄金比时,常常会给人以一种优美的视觉感受,所以,设计许多物品时都含有黄金比这一因素。
3. 找一找除了a︰b之外还有其他线段长度符合黄金比吗?
2. 出示图片欣赏,介绍黄金比。
c
c
(c和a也符合黄金比)
化简比的根据是比的基本性质,化简比的结果是最简单的整数比;所谓最简单的整数比,是指前项和后项都是整数且互质。所以化简比先要把前项和后项同时化成整数,再化简成互质数。
三、课堂小结
四、巩固练习
一、把下面各比化成最简单的整数比。
32∶16
48∶40
0.15∶0.3
5
6
1
6
∶
7
12
3
8
∶
5
8
∶
0.125
2 : 1
6 : 5
1 : 2
5 : 1
14 : 9
1 : 5
四、巩固练习
二、判断正误。
1.比的前项和后项同时乘一个相同的数,比值不变。 ( )
2. 10克盐溶解在100克水中,这时盐和盐水的比是1 ∶10。( )
3. 比的前项乘5,后项除以 。比值不变。 ( )
×
×
5
1
×
六年级数学上册(RJ) 教学课件
第 3 课时 比 的 应 用
第 4 单元 比
1.口答。
(1)什么叫做比?
(2)500mL的 是多少毫升?
一、复习导入
1
5
两个数相除又叫做两个数的比。
500× =100(毫升)
1
5
一、复习导入
2.六(1)班40名学生参加大扫除,其中 的同学打扫教室, 的同学打扫操场。
(1)打扫教室、操场的同学各有多少人?
(2)写出打扫教室、操场的人数比。
3
8
5
8
40× =15(人)
3
8
40× =25(人)
5
8
15 : 25 = 3 : 5
二、探究新知
这是某种清洁剂浓缩液的稀释瓶,瓶子上标明的比表示浓缩液和水的体积之比。按照这些比,可以配制出不同浓度的稀释液。
我按1∶4的比配制了一瓶500mL的稀释液,其中浓缩液和水的体积分别是多少?
1∶3
1∶4
1∶5
2
二、探究新知
明确意义
在工农业生产和日常活动中,有时并不是把一个数量平均分配,而是需要把一个数量平均分配,而是需要把一个数量按照一定比来分配。从某种意义上说,平均分是按一定的比分配的特例,按一定的比分配则是平均分的发展。例如:把一个数量平均分成2份,也就是说成把这个数量按1∶1进行分配。
二、探究新知
理解题意
500mL是配好后的稀释液的体积,1∶4表示……
要求的是……
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}已知条件
按1∶4的比例配置了一瓶500mL的稀释液
所求问题
浓缩液和谁的体积分别是多少
我按1∶4的比配制了一瓶500mL的稀释液,其中浓缩液和水的体积分别是多少?
信息提取
二、探究新知
关键条件理解
500毫升稀释液
浓缩液
1份
水
4份
1∶4表示在500mL的稀释液中,浓缩液占1份,水占4份,一共是5份。
理解题意
我把总体积平均分成5份……
浓缩液占总体积的 。
1
1+4
每份是:500÷5=100(mL)
浓缩液有:100×1=100(mL)
水有:100×4=400(mL)
浓缩液有: 500× =100(mL)
水有:500× =( )(mL)
1∶4
1
1+4
( )
( )
4
5
400
二、探究新知
浓缩液
水
探究解题方法
二、探究新知
探究解题方法
解答
500÷5=100(mL)
100×1=100(mL)
100×4=400(mL)
方法一:
方法二:
500× =100(mL)
1
1+4
500× =400(mL)
1
1+4
答:水的体积是400mL,浓缩液的体积是100mL。
要看清楚1∶4到底是哪两个量之间的比。
浓缩液体积∶水的体积
=( )∶( )
=( )∶( )
100mL 400mL
1 4
答:浓缩液有 mL,水有 mL。
100 400
二、探究新知
回顾与反思
三、课堂小结
解决按比分配问题,,可以先求出总份数,再求出一份是多少,然后求各部分的量;还可以先求出各部分量占总量的百分之几,再求各部分的量。
四、巩固练习
爸爸用一根长108㎝的铁丝给亮亮做了一个长方体模型。这个模型长、宽、高的比是4:3:2,它的体积是多少立方厘米?
解:长 :108 × =48 宽 :108 × =36
高 :108 × =24
体积: 48×36×24=41472(立方厘米)
答:它的体积是41472立方厘米。
9
4
9
3
9
2
四、巩固练习
某妇产科医院上月新生婴儿303名,男女婴儿人数之比是51︰50。上月新生男女婴儿各有多少人?
答:上月新生男婴儿有153人,女婴儿有150人。
方法一:
51+50=101
303÷101=3(人)
3×51=153(人)
3×50=150(人)
101
51
101
50
方法二:
51+50=101
303× =153(人)
303× =150(人)
四、巩固练习
学校把栽70棵树的任务,按照六年级三个班的人数分配给各班。一班46人,二班44人,三班50人。三个班各应栽树多少棵?
方法一:
46︰44︰50= 23︰22︰25 23+22+25=70
70÷70=1(棵)
一班:1×23=23(棵) 二班:1×22=22(棵)
三班:1×25=25(棵)
23+22+25
23
23+22+25
22
23+22+25
25
方法二:
46︰44︰50= 23︰22︰25
一班:70× =23(棵)
二班:70× =22(棵)
三班:70× =25(棵)
四、巩固练习
46+44+50
46
46+44+50
44
46+44+50
25
方法三:
一班:70× =23(棵)
二班:70× =22(棵)
三班:70× =25(棵)
方法四:
46+44+50=140(人) 140÷70=2(人)
一班:46÷2=23(棵) 二班:44÷2=22(棵)
三班:50÷2=25(棵)
答:一班栽树23棵,二班栽树22棵,三班栽树25棵。
学校把栽70棵树的任务,按照六年级三个班的人数分配给各班。一班46人,二班44人,三班50人。三个班各应栽树多少棵?
第 1 课时 比 的 意 义
第 4 单元 比
2003年10月15日,我国第一艘载人飞船“神舟”五号顺利升空。在太空中,执行此次任务的航天员杨利伟在飞船里向人们展示了联合国旗和中华人民共和国国旗。
一、创设情境,引入新课
一、创设情境,引入新课
提问:
(1)图上画了些什么?你了解到了哪些信息?有何感想?
(2)根据画面情境,你想提出什么问题?
(3)杨利伟在载人飞船上向人们展示的两面国旗的长和宽是多少?你是怎样用算式表示它们的关系的?
杨利伟展示的两面旗都是长15cm,宽10cm。怎样用算式表示它们长和宽倍数的关系?
一、创设情境,引入新课
可以用“15÷10”表
示长是宽的多少倍。
也可以用“10÷15”表
示宽是长的几分之几。
有时我们也把这两个数量之间的关系说成:
长和宽的比是15比10,宽和长的比是10比15.
一、创设情境,引入新课
“神舟”五号进入运行轨道后,在距地350km的高空做圆周运动,平均90分钟绕地球一周,大约运行42252km。
怎样用算式表示飞船进入轨道后
平均每分钟飞行多少千米?
速度可以用“路程÷时间”表示。
二、探究新知
我们也可以用比来表示路程和时间的关系:
路程和时间的比是42252比90。
两个数的比表示两个数相除。
15比10记作15∶10
10比15记作10∶15
42252比90记作42252∶90
“∶”是比号。
二、探究新知
在两个数的比中,比号前面的数叫做比的前项,比号后面的数叫做比的后项。比的前项除以后项所得的商,叫做比值。例如:
3
2
15 ∶ 10 = 15 ÷ 10 =
……
前
项
……
比号
……
后项
……
比值
比值通常用分数表示,也可以用小数或整数表示。
根据分数与除法的关系,两个数的比也可以写成分数形式。例如:15∶10也可以写成 ,仍读作“15比10”。
15
10
除 法
被除数
÷
除 数
商
分 数
分 子
—
分 母
分数值
比
前 项
∶
后 项
比 值
1.
三 、课堂小结
2.
比与分数、除法的内在联系十分紧密,但又有区别。除法是一种运算,分数是一种数,比是表示两个数之间的关系,它们各有不同的意义。所以在说它们之间关系的时候,要说“相当于”,而不能说“等于”或“是”。
三、课堂小结
1.小敏和小亮在文具店买同样的练习本。小敏买了6本,共花了1.8元。小亮买了8本,共花了2.4元。
小敏和小亮买的练习本数之比是( )∶( ),比值是( );
花的钱数之比是( )∶( ),比值是( )。
2. 3∶( )=24 ( )∶8=0.5
1
8
6
8
0.75
1.8
2.4
0.75
4
四、巩固练习
3.你还记得商不变的规律和分数的基本性质吗?
被除数和除数同时乘或除以相同的数……
分数的分子和分母同时乘或除以相同的数……
商不变的规律:被除数和除数同时乘或除以相同的数(0除外),商不变。
分数的基本性质:分数的分子和分母同时乘或除以相同的数(0除外),分数的大小不变。
四、巩固练习
四、巩固练习
六年级(5)班有男生20人,女生18人,求下列各比。
(1) 男生人数∶女生人数;
(2) 女生人数∶全班人数;
(3) 男生人数∶全班人数。
(1) 10 ∶9 (2)9∶19
(3)10 ∶19
六年级数学上册(RJ) 教学课件
第 2 课时 比 的 基 本 性 质
第 4 单元 比
一、复习导入
小明、小强、小丽都喜欢制作折纸。有一天,他们三人在争论谁每分钟折的纸鹤数多?
小明说:“我八分钟折了六只。”
小强说:“我四分钟折了三只。”
小丽说:“我十六分钟折了十二只。”
问题:小明、小强和小丽折的只数和时间(分)的比是多少?
小明6∶8 小强3∶4 小丽12∶16
谁折的速度快呢?
联系比和除法、分数的关系,想一想:在比中有什么样的规律?
二、探究新知
先利用比和除法的关系来研究。
6∶8=6÷8= =
6
8
3
4
12∶16=12÷16= =
12
16
3
4
6∶8=(6×2)÷(8×2)=12÷16
6∶8=(6×2)∶(8×2)=12∶16
6∶8=(6÷2)∶(8÷2)=3∶4
6÷8=(6÷2)÷(8÷2)=3÷4
二、探究新知
你能根据比和分数的关系研究比中的规律吗?
比的前项和后项同时乘或除以相同的数(0除外),比值不变。这叫做比的基本性质。
根据比的基本性质,可以把比化成最简单的整数比。
二、探究新知
(1)“神舟”五号搭载了两面联合国旗,一面长15cm,宽10cm(前面展示过),另一面长180cm,宽120cm(如图)。
1
15cm
10cm
180cm
120cm
这两面联合国旗长和宽的最简单的整数比分别是多少?
15∶10 =(15÷5)∶(10÷5)
= 3∶2
180∶120 =(180÷ )∶(120÷ )
=( )∶( )
想:5是15和10的什么数?为什么要除以5?
60
60
3
2
二、探究新知
(2)把下面各比化成最简单的整数比。
想:为什么要乘18?
0.75∶2=(0.75×100)∶(2×100)
= 75∶200
=( )∶( )
∶ =( ×18)∶( ×18)
=( )∶( )
1
6
2
9
∶
0.75∶2
1
6
2
9
1
6
2
9
3
4
3
8
二、探究新知
当一个比的前项或后项不是整数时,怎样把它化成最简单的整数比?
分数比的化简方法:(1)比的前项和后项同时乘它们分母的最小公倍数,转化成整数比,再进行化简。(2)利用求比值的方法也可以化简分数比,但结果必须写成比的形式。
小数比的化简方法:先把比的前项和后项的小数点同时向右移动相同的位数,转化成整数比,再按照整数比的化简方法进行化简。
二、探究新知
二、探究新知
介绍黄金比:
问题:1. 你听说过“黄金比”吗?
4. 你还了解生活中的黄金比吗?课下查阅相关的资料。
把一条线段分成两部分,如果较短部分与较长部分长度之比等于较长部分与整体长度之比,我们把这个比称为黄金比(约为 0.618︰1)。当一个物体的两个部分长度的比大致符合黄金比时,常常会给人以一种优美的视觉感受,所以,设计许多物品时都含有黄金比这一因素。
3. 找一找除了a︰b之外还有其他线段长度符合黄金比吗?
2. 出示图片欣赏,介绍黄金比。
c
c
(c和a也符合黄金比)
化简比的根据是比的基本性质,化简比的结果是最简单的整数比;所谓最简单的整数比,是指前项和后项都是整数且互质。所以化简比先要把前项和后项同时化成整数,再化简成互质数。
三、课堂小结
四、巩固练习
一、把下面各比化成最简单的整数比。
32∶16
48∶40
0.15∶0.3
5
6
1
6
∶
7
12
3
8
∶
5
8
∶
0.125
2 : 1
6 : 5
1 : 2
5 : 1
14 : 9
1 : 5
四、巩固练习
二、判断正误。
1.比的前项和后项同时乘一个相同的数,比值不变。 ( )
2. 10克盐溶解在100克水中,这时盐和盐水的比是1 ∶10。( )
3. 比的前项乘5,后项除以 。比值不变。 ( )
×
×
5
1
×
六年级数学上册(RJ) 教学课件
第 3 课时 比 的 应 用
第 4 单元 比
1.口答。
(1)什么叫做比?
(2)500mL的 是多少毫升?
一、复习导入
1
5
两个数相除又叫做两个数的比。
500× =100(毫升)
1
5
一、复习导入
2.六(1)班40名学生参加大扫除,其中 的同学打扫教室, 的同学打扫操场。
(1)打扫教室、操场的同学各有多少人?
(2)写出打扫教室、操场的人数比。
3
8
5
8
40× =15(人)
3
8
40× =25(人)
5
8
15 : 25 = 3 : 5
二、探究新知
这是某种清洁剂浓缩液的稀释瓶,瓶子上标明的比表示浓缩液和水的体积之比。按照这些比,可以配制出不同浓度的稀释液。
我按1∶4的比配制了一瓶500mL的稀释液,其中浓缩液和水的体积分别是多少?
1∶3
1∶4
1∶5
2
二、探究新知
明确意义
在工农业生产和日常活动中,有时并不是把一个数量平均分配,而是需要把一个数量平均分配,而是需要把一个数量按照一定比来分配。从某种意义上说,平均分是按一定的比分配的特例,按一定的比分配则是平均分的发展。例如:把一个数量平均分成2份,也就是说成把这个数量按1∶1进行分配。
二、探究新知
理解题意
500mL是配好后的稀释液的体积,1∶4表示……
要求的是……
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}已知条件
按1∶4的比例配置了一瓶500mL的稀释液
所求问题
浓缩液和谁的体积分别是多少
我按1∶4的比配制了一瓶500mL的稀释液,其中浓缩液和水的体积分别是多少?
信息提取
二、探究新知
关键条件理解
500毫升稀释液
浓缩液
1份
水
4份
1∶4表示在500mL的稀释液中,浓缩液占1份,水占4份,一共是5份。
理解题意
我把总体积平均分成5份……
浓缩液占总体积的 。
1
1+4
每份是:500÷5=100(mL)
浓缩液有:100×1=100(mL)
水有:100×4=400(mL)
浓缩液有: 500× =100(mL)
水有:500× =( )(mL)
1∶4
1
1+4
( )
( )
4
5
400
二、探究新知
浓缩液
水
探究解题方法
二、探究新知
探究解题方法
解答
500÷5=100(mL)
100×1=100(mL)
100×4=400(mL)
方法一:
方法二:
500× =100(mL)
1
1+4
500× =400(mL)
1
1+4
答:水的体积是400mL,浓缩液的体积是100mL。
要看清楚1∶4到底是哪两个量之间的比。
浓缩液体积∶水的体积
=( )∶( )
=( )∶( )
100mL 400mL
1 4
答:浓缩液有 mL,水有 mL。
100 400
二、探究新知
回顾与反思
三、课堂小结
解决按比分配问题,,可以先求出总份数,再求出一份是多少,然后求各部分的量;还可以先求出各部分量占总量的百分之几,再求各部分的量。
四、巩固练习
爸爸用一根长108㎝的铁丝给亮亮做了一个长方体模型。这个模型长、宽、高的比是4:3:2,它的体积是多少立方厘米?
解:长 :108 × =48 宽 :108 × =36
高 :108 × =24
体积: 48×36×24=41472(立方厘米)
答:它的体积是41472立方厘米。
9
4
9
3
9
2
四、巩固练习
某妇产科医院上月新生婴儿303名,男女婴儿人数之比是51︰50。上月新生男女婴儿各有多少人?
答:上月新生男婴儿有153人,女婴儿有150人。
方法一:
51+50=101
303÷101=3(人)
3×51=153(人)
3×50=150(人)
101
51
101
50
方法二:
51+50=101
303× =153(人)
303× =150(人)
四、巩固练习
学校把栽70棵树的任务,按照六年级三个班的人数分配给各班。一班46人,二班44人,三班50人。三个班各应栽树多少棵?
方法一:
46︰44︰50= 23︰22︰25 23+22+25=70
70÷70=1(棵)
一班:1×23=23(棵) 二班:1×22=22(棵)
三班:1×25=25(棵)
23+22+25
23
23+22+25
22
23+22+25
25
方法二:
46︰44︰50= 23︰22︰25
一班:70× =23(棵)
二班:70× =22(棵)
三班:70× =25(棵)
四、巩固练习
46+44+50
46
46+44+50
44
46+44+50
25
方法三:
一班:70× =23(棵)
二班:70× =22(棵)
三班:70× =25(棵)
方法四:
46+44+50=140(人) 140÷70=2(人)
一班:46÷2=23(棵) 二班:44÷2=22(棵)
三班:50÷2=25(棵)
答:一班栽树23棵,二班栽树22棵,三班栽树25棵。
学校把栽70棵树的任务,按照六年级三个班的人数分配给各班。一班46人,二班44人,三班50人。三个班各应栽树多少棵?
