人教版数学六年级上册:第1单元 分数乘法 课件(共94张PPT)
文档属性
| 名称 | 人教版数学六年级上册:第1单元 分数乘法 课件(共94张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-23 16:28:52 | ||
图片预览





文档简介
六年级数学上册(RJ) 教学课件
第 1 课时 分数乘法的意义(1)
第 1 单 元 分 数 乘 法
一、复习导入
(1)5个12是多少?
(2)
5×12=60
1.计算下列各题。
1
6
+
2
6
3
6
+
=
1
(3)
3
10
+
+
=
9
10
3
10
3
10
二、探究新知
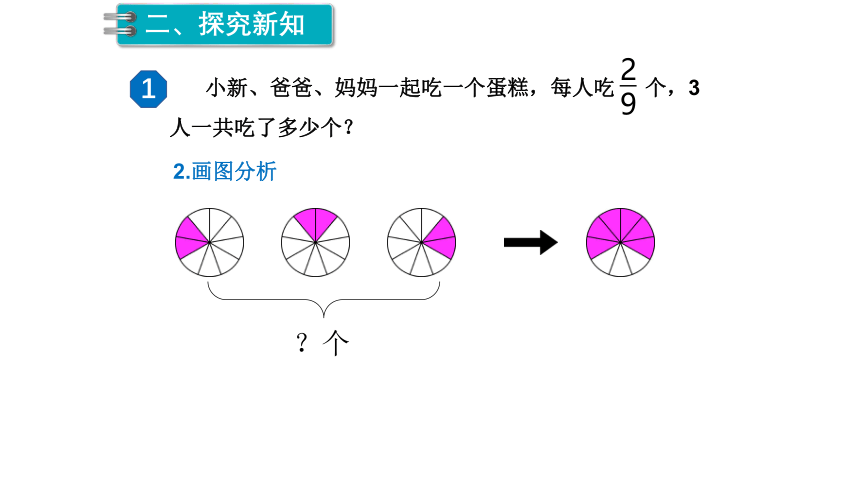
1
小新、爸爸、妈妈一起吃一个蛋糕,每人吃 个,3人一共吃了多少个?
2
9
1.梳理信息,分析思路
问题:(1) 你知道了什么?
(2) 你能试着用图表示出题意吗?
二、探究新知
?个
2.画图分析
1
小新、爸爸、妈妈一起吃一个蛋糕,每人吃 个,3人一共吃了多少个?
2
9
二、探究新知
2
9
+
2
9
+
2
9
=
6
9
2
3
(个)
=
3.探究分数乘整数的意义
(1)求3个 是多少可以怎样列式?
9
2
(2)还可以怎样列式?
3个 相加,用乘法表示就是 ×3或 3× 。
2
9
2
9
2
9
分数乘整数的意义和整数乘法的意义相同,就是求几个相同加数的和的简便计算
二、探究新知
2
9
2×3
9
×3
6
9
(个)
=
=
2
9
+
2
9
+
2
9
=
2+2+2
9
=
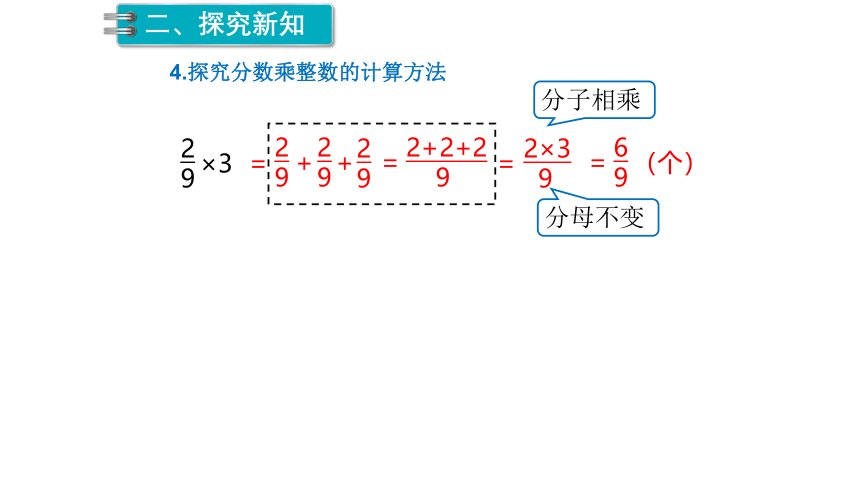
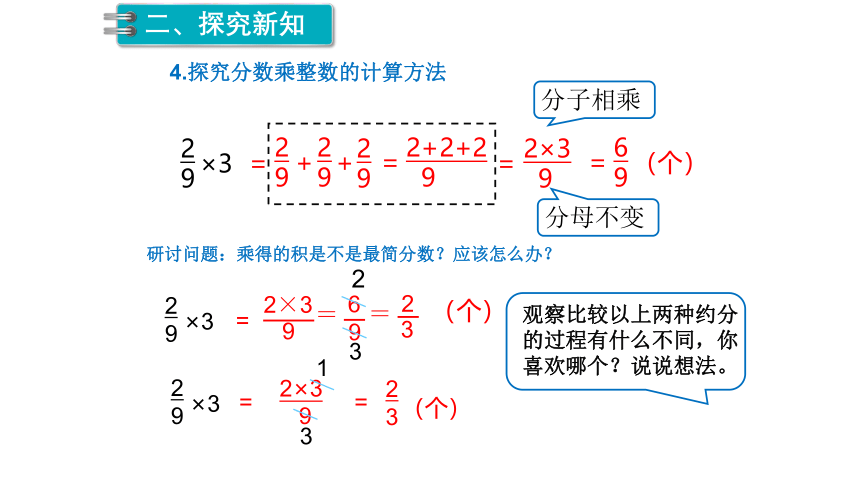
4.探究分数乘整数的计算方法
分子相乘
分母不变
二、探究新知
2
9
2×3
9
×3
6
9
(个)
=
=
2
9
+
2
9
+
2
9
=
2+2+2
9
=
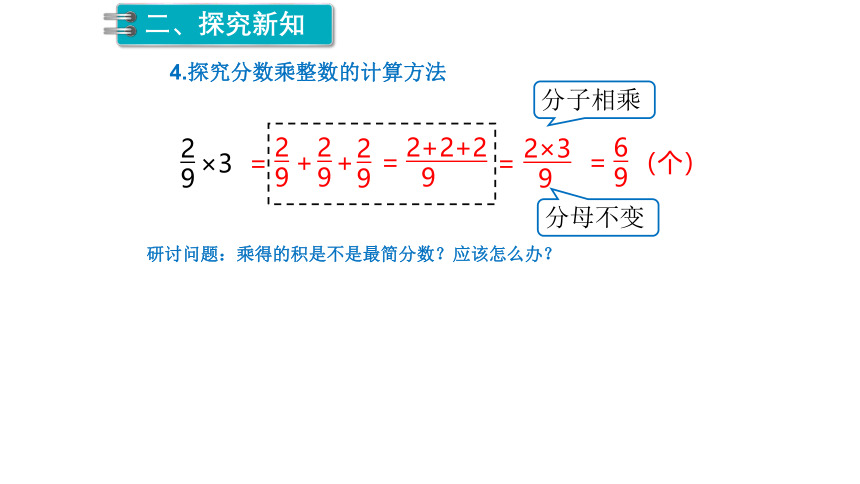
4.探究分数乘整数的计算方法
研讨问题:乘得的积是不是最简分数?应该怎么办?
分子相乘
分母不变
二、探究新知
2
9
2×3
9
×3
6
9
(个)
=
=
2
9
+
2
9
+
2
9
=
2+2+2
9
=
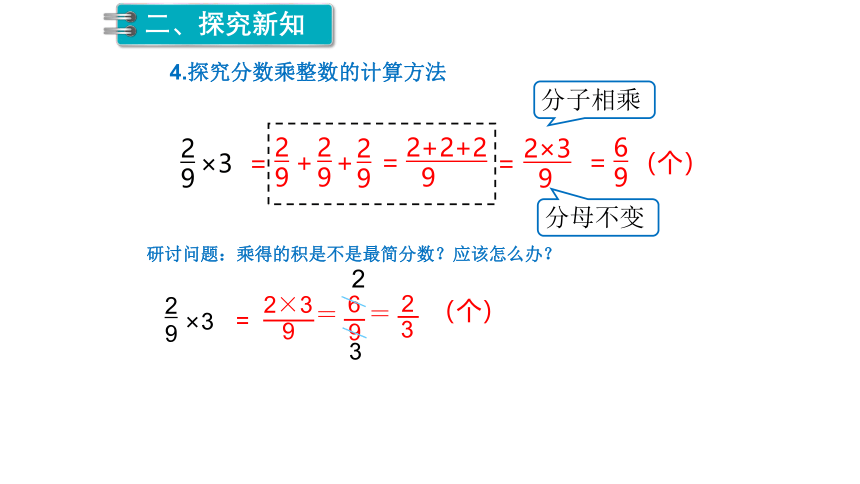
4.探究分数乘整数的计算方法
研讨问题:乘得的积是不是最简分数?应该怎么办?
9
2×3
=
9
6
2
9
×3
=
分子相乘
分母不变
2
3
=
3
2
(个)
二、探究新知
2
9
2×3
9
×3
6
9
(个)
=
=
2
9
+
2
9
+
2
9
=
2+2+2
9
=
4.探究分数乘整数的计算方法
研讨问题:乘得的积是不是最简分数?应该怎么办?
9
2×3
=
9
6
2
3
=
3
2
(个)
2×3
9
2
3
1
3
2
9
×3
=
(个)
=
2
9
×3
=
分子相乘
分母不变
观察比较以上两种约分的过程有什么不同,你喜欢哪个?说说想法。
二、探究新知
2.能先约分的可以先约分,再计算,结果相同。
1.分数乘整数,用分子乘整数的积作分子,分母
不变。
分数与整数相乘,
是怎样计算的?
5.讨论总结
三、巩固练习
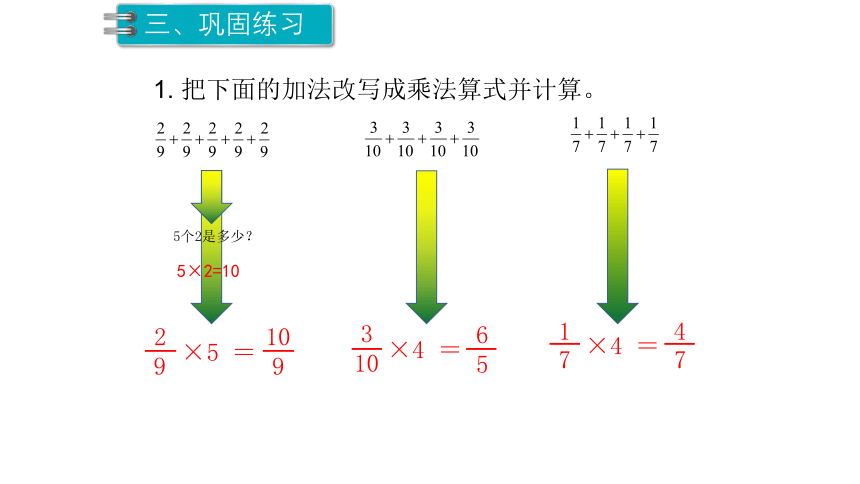
1. 把下面的加法改写成乘法算式并计算。
×5 =
9
2
9
10
×4 =
10
3
5
6
×4 =
7
1
7
4
5个2是多少?
5×2=10
三、巩固练习
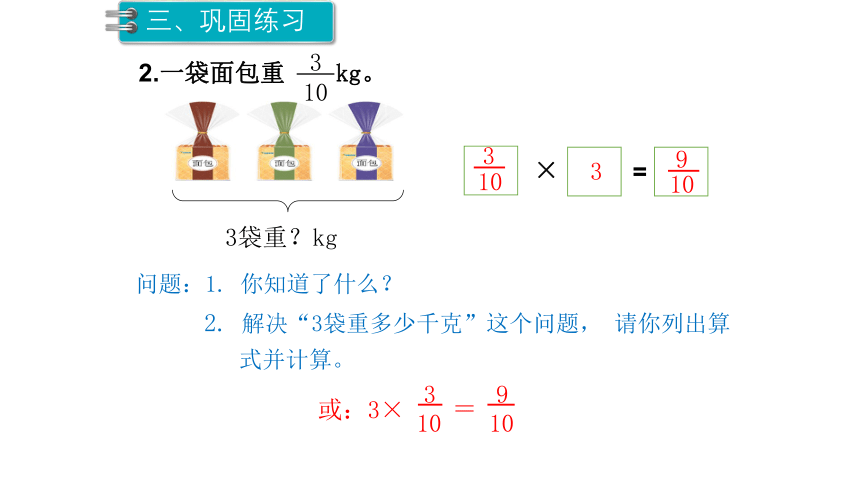
3袋重?kg
问题:1. 你知道了什么?
2. 解决“3袋重多少千克”这个问题, 请你列出算
式并计算。
或:3×
10
3
10
9
=
2.一袋面包重 kg。
3
10
×
=
3
10
3
10
9
三、巩固练习
3.直接说出得数。
问题:直接说出得数,并说说你是怎样想的。
=0
×4
15
2
×8
12
5
×4
9
2
×1
7
2
×0
3
2
2×
4
3
15
8
=
=
3
10
=
2
3
=
7
2
=
9
8
四、作业布置
作业:第6页练习一,
第1题、第2题、第3题。
六年级数学上册(RJ) 教学课件
第 2 课时 分数乘法的意义(2)
第 1 单 元 分 数 乘 法
一、复习导入
1.计算下面各题。
说说计
算方法。
3
7
2
×
1
10
3
×
3
15
5
×
6
7
3
10
3
5
=
=
=
2.说说分数乘整数的意义是什么。
二、探究新知
1桶水有12L。
3桶共多少升?
1.你知道了什么?
2.要求“3桶水共重多少升”
怎样列式?
(求3个12L,就是求12L的3倍是多少。)
2
1.出示问题
12×3
你是怎么
想的?
二、探究新知
桶是多少升?
1
2
问题:1.你知道了什么?
3.你是根据什么列式的?
表示求半桶水的体积,就是求12L
的一半,也就是求12L的 是多少。
2.要求“ 桶是多少升?”怎样列式?
1
2
1
12
×
每桶的体积×桶数=总体积
1
2
12
×
( )
( )
2
12
二、探究新知
桶是多少升?
1
4
1
4
12
×
问题:1.你知道了什么?
2.要求“ 桶是多少升?”怎样列式?
3.你是根据什么列式的?
1
4
每桶的体积×桶数=总体积
4. 表示求 桶水的体积,就是求12L的 。
1
4
12
×
1
4
( )
( )
1
4
二、探究新知
桶是多少升?
1
2
12
×
12
桶是多少升?
1
4
1
4
12
×
观察比较上面两个算式表示的意思有什么相同之处?
2.讨论总结
小结:一个数乘几分之几表示的是求这个数的几分之几是多少。
三、巩固新知
2.要求吃了多少千克,请你列出算式。
3.你是根据什么列出算式的?
一袋面粉重3kg。已经吃了它的 ,吃了多少千克?
3
10
×
(把一袋面粉平均分成10份,吃了的占3份。)
问题:1.你是怎样理解“已经吃了它的 ”这句话的?
3
10
(求3kg的 是多少。)
3
10
3
3
10
四、巩固练习
一个数(0除外)乘一个小于1的数,积小于这个数;乘一个大于的数,积大于这个数;乘1,积等于这个数。
<
>
=
判断大小,寻找规律
六年级数学上册(RJ) 教学课件
第 3 课时 分数乘分数(1)
第 1 单 元 分 数 乘 法
一、引入情景 探究新知
3
1
2
李伯伯家有一块 公顷的地。
种土豆的面积占这块地的 ,
种玉米的面积占 。
5
1
5
3
一、引入情景 探究新知
3
1
2
李伯伯家有一块 公顷的地。
种土豆的面积占这块地的 ,
种玉米的面积占 。
5
1
5
3
(1)种土豆的面积是多少公顷?
(2)种玉米的面积是多少公顷?
一、引入情景 探究新知
1.明确问题 提取信息
解决问题(1)种土豆的面积是多少公顷?
问题:1. 题目中的已知条件是什么?
5
1
2. 你是怎样理解“种土豆的面积占这块地的 ”这句话的意思的?
(把这块地平均分成5份,种土豆的面积占1份。)
1
5
占
1
2
公顷
一、引入情景 探究新知
2.分析题意,列式计算
2
1
5
1
2
1
5
1
×
求 公顷的 是多少,可以用乘法计算,列式为 。
(1)实践操作
3.探究计算方法
1
2
公顷
公顷的
1
5
1
2
1
2
×
1
5
1×1
2×5
1
10
(公顷)
=
=
1公顷
平均分成2份,
每份是 公顷
1
2
将 公顷平均
分成 5 份,
1
2
其中的1份占
1公顷的
1
10
1公顷的 即 公顷
1
10
1
10
(2)列式计算
一、引入情景 探究新知
解决问题(2)种玉米的面积是多少公顷?
1. 你是怎样理解“种玉米的面积占 ”这句话?
5
3
2. 怎样列式呢?
(把这块 地平均分成5份,种玉米的面积占3份。)
2
1
5
3
2
1
5
3
×
(求 公顷的 是多少,可以用 表示。)
一、引入情景 探究新知
3. 请你用一张纸动手折一折、画一画,用阴影表示出 的意思。
2
1
5
3
×
公顷
10
3
1
2
公顷
公顷的
3
5
1
2
公顷的 ,就是把 公顷平均分成5份,取其中的3份,也就是把1公顷平均分成(2×5)份,取其中的3份,平均分成(2×5)份,“取其中的3份”就乘“3”,用算式表示是
1
2
3
5
1
2
2×5
1
×3=
2×5
1×3
1
2
×
3
5
=
×
×
(公顷)
2
5
1
10
3
3
=
二、课堂小结
讨论:分数乘分数怎样计算?
用分母相乘的积作分母。
分数乘分数,用分子
相乘的积作分子。
三、巩固练习
(1) kg的 是多少千克?
×
(2) kg的 是多少千克?
1.只列式,不计算。
5
3
2
1
7
4
12
7
×
2
1
5
3
12
7
7
4
三、巩固练习
2.看图计算。(教材P5T2)
2
1
2
1
×
=
( )
( )
3
2
5
4
×
=
( )
( )
4
3
4
3
×
=
( )
( )
4
1
15
8
16
9
六年级数学上册(RJ) 教学课件
第 4 课时 分数乘分数(2)
第 1 单 元 分 数 乘 法
一、复习导入
1.口算下列各题。
3
8
4
×
2
5
5
×
1
10
2
×
3
2
2
1
5
=
=
=
1
6
5
×
3
23
8
×
3
7
2
×
3
2
24
23
6
7
=
=
=
一、复习导入
2.计算下列各题。
3
4
×
2
3
=
8
9
1
2
×
3
7
=
6
7
5
8
×
5
14
=
4
7
5
24
×
5
27
=
8
9
8
25
×
4
15
=
5
6
二、探究新知
9
10
(1)李叔叔的游泳速度是乌贼的 。李叔叔每分钟游多少千米?
4
45
4
无脊椎动物中游泳最快的是乌贼,
它的速度是 千米/分。
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A} 已知条件
所求问题
乌贼每分钟游 km
李叔叔每分钟游多少千米?
李叔叔每分钟游的距离是乌贼的
理解题意
9
10
4
45
二、探究新知
2.你是怎样理解“李叔叔的游泳速度是乌贼的 这句话的?
4
45
(把乌贼的速度平均分成45份,李叔叔的游泳速度有这样的4份。)
9
10
×
4
45
9×4
10×45
2
25
(km)
=
=
1
\
\
\
\
5
2
5
为了计算简便,可
以先约分再乘。
解法探究
二、探究新知
(2)乌贼30分钟可以游多少千米?
理解题意
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}已知条件
所求问题
速度
时间
路程
乌贼的游泳速度是 千米/分
30分钟
30分钟可以游多少千米
9
10
二、探究新知
1.要求乌贼30分钟可以游多少千米,怎样列式?
2.请你独立计算。
研讨问题:方法2和方法3
的约分方法你更喜欢哪个?
预设1:
10
9
×30=
10
9×30
=
10
270
预设2:
10
9
×30=
10
9×30
=
10
270
=27
27
1
预设3:
10
9
×30=
=27
10
9
×30
1
3
研讨问题:这个结果是不
是最简分数?
10
9
×30
(km)
(km)
(km)
解法探究
二、探究新知
小结:分数乘分数,用分子相乘的积作分子,用分母相乘的积作分母。
为了计算简便,可以先约分再乘。
你觉得分数乘法该怎样计算呢?
三、巩固练习
1.计算下面各题。
7
3
×21
7
16
×
48
35
11
19
×
38
33
11
9
×121
21
17
×
68
63
9
5
×
3
10
= 9
= 99
=
5
3
=
3
2
=
3
4
=
50
27
三、巩固练习
一个数(0除外)乘一个小于1的数,积小于这个数;乘一个大于的数,积大于这个数;乘1,积等于这个数。
<
>
=
2.判断大小,寻找规律
三、巩固练习
3. 蜂鸟是目前所发现的世界最小的鸟,也是唯一能倒飞的鸟。蜂鸟的飞行速度是 千米/分,
分钟飞行多少千米?5分钟飞行多少千米?
3
10
3
2
解: × = (千米) ×5 = (千米)
答: 分钟飞行 千米,5分钟飞行 千米。
3
2
10
3
10
3
5
1
2
3
3
2
5
1
2
3
三、巩固练习
4.下面是园林处三位职工铺草坪的情况
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}姓名
王伟
李红
徐光
每小时铺的面积/平方米
6
铺的时间/时
4
3
5
27
3
4
2
15
5
6
他们分别铺了多少平方米?
思路分析:每小时铺的面积是工作效率,铺的时间是工作时间,铺了的面积是工作总量。根据工作效率×工作时间=工作总量可分别列式解答。王伟的工作效率是每小时铺6平方米,工作时间是 ,求工作总量,列式为 。李红和徐光的工作总量的求法相同。
4
3
解答:
王伟:6 × = (平方米)
李红: × = (平方米)
徐光: × = 9(平方米)
4
3
2
9
3
2
36
5
6
2
15
4
5
27
四、拓展训练
a、b是不为0的整数,a×a,求b的值。
3
b
5
b
思路分析:由一个不为0的数乘小于1的数,得数小于他本身,可知a×a中的 >1,所以b>3。因为b是不为0的整数,且大于3,小于5,所以b是4。
5
b
5
b
3
b
3
b
六年级数学上册(RJ) 教学课件
第 5 课时 分 数 乘 小 数
第 1 单元 分数乘法
1.求下面各题的商。(分别用小数、分数表示)
一、复习导入
5÷10= 9÷100=
37÷1000= 2÷10=
20÷100= 50÷1000=
0.5=
1
2
0.09=
9
100
0.037=
37
1000
0.2=
1
5
0.2=
1
5
0.05=
1
20
我身体长2.1dm。
欢欢
二、探究新知
可以把2.1化成分数,
也可以把 化成小数。
(1)松鼠欢欢的尾巴有多长?
松鼠的尾巴长度约占身体长度的 。
3
4
3
4
×
=
3
4
2.1
(dm)
1.575
0.75
5
我身体长2.4dm。
松鼠的尾巴长度约占身体长度的 。
3
4
(2)松鼠乐乐的尾巴有多长?
×
=
3
4
2.4
×
3
4
2.4
\
\
=
1.8(dm)
0.6
1
这样约分计
算真简便。
你是怎样计算的?和同学交流一下你的方法。
小结:在计算小数乘分数时 ,可以把小数化成分数,可以把分数化成小数,也可以直接约分计算。要注意在计算时能约分的要先约分。
三、课堂小结
四、巩固练习
3
5
3
5
5
6
5
6
1.2× =
2.5× =
1.4× =
2.4× =
18
25
3
2
7
6
2
四、巩固练习
=
=
=
=
=
=
12
25
27
25
161
40
381
70
18
5
2
75
六年级数学上册(RJ) 教学课件
第 6 课时 分数混合运算
第 1 单元 分数乘法
1.计算下面各题。
一、复习导入
15×(34-29)=
16×4-7×9=
70-4×6=
75
1
46
2.用简便方法计算下面各题。
2.5×98×0.4 1.25×2.5×8×4
=98
(8+0.8)×12.5
=110
=100
1
2
m
4
5
m
二、探究新知
预设1:
5
4
( + )×2
2
1
预设2:
5
4
×2+ ×2
2
1
问题:1. 分数混合运算的顺序和整数混合运算的顺序相同,
你会自己计算上面这两道算式吗?
2. 通过计算你有什么发现?
5
4
( + )×2=
2
1
5
4
×2+ ×2
2
1
6
一个画框的尺寸如右图,做这个画框需要多长的木条?
观察每组的两个算式,看看它们有什么关系。
×
3
1
2
1
×
2
1
3
1
4
1
( × )×
3
2
5
3
4
1
×( × )
3
2
5
3
2
1
( + )×
3
1
5
1
2
1
× + ×
3
1
5
1
5
1
=
=
=
小结:整数乘法的交换律、结合律和分配律,对于
分数乘法也适用。
从这些算式中,你发现了什么规律?
三、课堂小结
1.商店运来一些水果,运来苹果20筐,梨的筐数是苹果的 ,同时橘子的筐数又是梨的 。运来橘子多少筐?
4
3
5
3
解:20× ×
= 20×( × )= 9(筐)
答:运来的橘子有9筐。
3
5
3
4
3
4
3
5
四、巩固训练
2.超市购进一批酸奶共30盒,每盒有8杯,每杯酸奶 升,
这批酸奶一共有多少升?
4
15
解:30×8×
=64(升)
答:这批酸奶一共有64升。
15
4
六年级数学上册(RJ) 教学课件
第 7 课时 分数简便运算
第 1 单元 分数乘法
一、复习导入
= ×4×5+ ×4×5
4
1
5
1
=9
= ×( + )
7
5
4
1
4
3
=
7
5
计算。
二、探究新知
研讨问题:你运用了什么运算定律?(乘法交换律和乘法结合律。)
研讨问题:你是怎样想的?(先做小括号里的,再做括号外的。)
问题:请你先独立计算上面两道题。
预设1:
5
3
×( ×5)=
6
1
×
6
5
5
3
=
2
1
1
1
1
2
1
预设2:
( ×5) × =
5
3
6
1
=
5
3
×( ×5)=
6
1
2
1
1
×
6
1
3
1
2
6
5
( + )×12
4
1
5
3
×( ×5)
6
1
7
研讨问题:你运用了什么运算定律?(运用乘法分配律,计算简便。)
小结:整数乘法的交换律、结合律和分配律,对于分数乘法也适用。
应用乘法的运算定律,可以使一些计算简便。
研讨问题:你是怎样想的?(先做小括号里的,再做括号外的。)
观察这2种计算方法,你喜欢哪种方法?说说你的想法。
6
5
( + )×12
4
1
预设1:
( + )×12
6
5
( + )×12
4
1
=
12
10
12
3
12
13
= ×12=13
1
1
=
预设2:
×12 + ×12
6
5
( + )×12
4
1
=10+3=13
6
5
4
1
2
1
3
1
三、课堂小结
从这些算式中,你发现了什么规律?
小结:分数混合运算时,要善于结合数据特点,灵活运用乘法的运算定律,使计算更简便。
×27+
9
8
27
×27
=
3
2
× ×3
4
=
1. 用简便方法计算下面各题,并说一说运用了什么运算定律。
3
2
× ×3
4
1
( + )×27
9
8
27
4
=(1+86)×
86
3
2
1
1
1
1
2
1
=
=24+4
=28
4
=
86
3
+3
=3
86
3
1× +86×
86
3
86
3
=
87×
86
3
四、巩固练习
四、巩固练习
2. 奶牛场每头奶牛平均日产牛奶 t,42头奶牛100天可产奶多少吨?
50
1
×42×100
50
1
×42×100
50
1
2
1
= 84(t)
=
六年级数学上册(RJ) 教学课件
第 8 课时 解 决 问 题(1)
第 1 单元 分数乘法
(4)母鸡的只数相当于公鸡的 。
(1)乙数是甲数的 。
(2)乙数的 相当于甲数。
(3)母鸡只数 等于小鸡的只数。
1
3
4
5
1
3
4
5
下面各题分别把谁看作单位“1”?
一、复习导入
其中一半种各种萝卜。红萝卜地的面积占整块萝卜地的 。
1
4
大棚共480m2
二、探究新知
红萝卜地有多少平方米?
8
理解题意
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
已知条件
整个大棚的面积是 480m2 。
萝卜地的面积占整个大棚面积的 。
红萝卜地的面积占萝卜地面积的 。
所求问题
红萝卜地的面积是多少平方米。
2
1
4
1
(1)怎样理解“其中的一半种各种萝卜”?
(2)怎样理解“红萝卜地的面积占整块萝卜地的 ”?
4
1
红萝卜地有多少平方米?
(把这块地平均分成2份,其中1份种各种萝卜)
(把种各种萝卜的面积平均分成4份,红萝卜占其中的1份。)
分析与解答
其中一半种各种萝卜。红萝卜地的面积占整块萝卜地的 。
1
4
大棚共480m2
8
方法探究
红萝卜地有多少平方米?
480m2
红萝卜地占萝卜地面积的
1
4
各种萝卜地占大棚面积的
1
2
(3)你能用示意图表示出题目的意思吗?
(4)请你解答这道题。
研讨问题:请你结合图说说你是怎样想的。
(先求出萝卜地的面积,再求出红萝卜地的面积。)
两种方法虽然不同,可以用一个综合算式表示:
480× × =60(m2)
2
1
预设1:
2
1
480× =240(m2)
4
1
240× =60(m2)
预设2:
×
4
1
2
1
=
8
1
8
1
480× =60(m2)
4
1
分析与解答
刚才用两种方法求出了红萝卜的面积,那么对不对呢?都可以怎样检验?
研讨问题:请你结合图说说你检验的思路。
(红萝卜的面积乘4表示萝卜地的面积,再乘2就是大棚的面积)
研讨问题:请你结合图说说你检验的思路。
(把大棚面积平均分成8份,红萝卜地占1份,用1份的面积
乘8就是大棚的面积。)
预设1:
60×4×2=480( )
预设2:
60×(4×2)=480( )
回顾与反思
回顾与反思
规范解答
解:480× × =60(m2)
答:红萝卜地有60m2。
2
1
2
1
分析与解答
其中一半种各种萝卜。红萝卜地的面积占整块萝卜地的 。
1
4
大棚共480m2
8
红萝卜地有多少平方米?
三、巩固练习
小亮的储蓄箱中有18元,小华储蓄的钱是小亮的 ,小新储蓄的钱是小华的 。小新储蓄了多少元?
6
5
3
2
解:18× × =10(筐)
答:小新储蓄了10元。
5
6
2
3
四、课堂小结
通过前面的学习,你有什么发现吗?
1.求一个数的几分之几是多少,属于两个量相比的关系。用线段图可以比较清楚地表示出数量之间的关系:
单位“1”的量×比较量占单位“1”的几分之几=比较量
2.解决连续求一个数的几分之几是多少的实际问题,弄清每一步单位“1”的量是谁最关键的。
六年级数学上册(RJ) 教学课件
第 9 课时 解 决 问 题(2)
第 1 单元 分数乘法
一、情境导入,探究新知
人心脏跳动的次数随年龄而变化。青少年心跳每分钟约75次,婴儿每分钟心跳的次数比青少年多 。婴儿每分钟心跳多少次?
5
4
9
理解题意
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
已知条件
青少年每分钟心跳约75次。
婴儿每分钟心跳的次数比青少年多 ,多的部分是婴儿的。
所求问题
婴儿每分钟心跳的次数。
5
4
(2)这道题怎样解答,请你根据题意先画出线段图。
(1)怎样理解“婴儿每分钟心跳的次数比青少年多 ”?
婴儿每分钟心跳次数与青少年心跳次数相比较,把青少
年每分钟心跳次数看作单位“1”;多的部分是青少年心
跳次数的 ,婴儿每分钟心跳次数是(1+ )。
5
4
5
4
5
4
分析与解答
解法探究
青少年:
婴儿:
?次
75次
比青少年多
4
5
分析与解答
研讨问题:请你结合图说说你是怎样想的。
求婴儿每分钟心跳次数就是求青少年的(1+ )是多少。
研讨问题:请你结合图说说你是怎样想的。(先求出婴儿比青少年多的,再
加上青少年每分钟心跳的次数,就是婴儿每分钟心跳的次数。)
预设1:
75+75× =75+60=135(次)
5
4
预设2:
75×(1+ )=75× =135(次)
5
4
5
9
5
4
回顾与反思
问题:1. 两种解题思路有什么不同?
2. 刚才用两种方法求出了婴儿的每分钟心跳次数,那么对不对呢?
可以怎样检验?
(135-75)÷75
75+75× =75+60=135(次)
5
4
5
9
5
4
75×(1+ )=75× =135(次)
5
4
青少年:
婴儿:
135次
75次
比青少年多?
= 60 ÷ 75
=
回顾与反思
小结:虽然两种解法不同,但都是依据了分数乘法的意义解决稍复杂的求一个数的几分之几是多少的问题。
75+75× =75+60=135(次)
5
4
规范解答
答:婴儿每分钟135。
二、课堂小结
“已知一个数比另一个数多几分之几,求这个数”的解题方法有两种:
(1)单位“1”的量+单位“1”的量×比单位“1”多的几分之几=所求的量
(2)单位“1”的量×(1+比单位“1”多的几分之几)=所求的量
三、巩固练习
1.一袋大米重25千克,先吃去这袋大米的 ,又吃去剩下的 千克,两次一共吃去多少千克?
5
1
5
1
解:25× =5(千克)
25× × =1(千克)
5+1=6(千克)
答:两个一共吃去了6千克。
1
5
1
5
1
5
2.一台笔记本电脑,先降价 ,后来又提价 。现价与原价相比是升了还是降了?
9
1
9
1
解:假设原价为“1”,那么现价为:
1×(1- )×(1 + )
=
因为 <1,所以现价与原价相比降了
答:现价与原价相比降了。
9
1
9
1
81
80
81
80
六年级数学上册(RJ) 教学课件
第 10 课时 整 理 和 复 习
第 1 单元 分数乘法
分数乘法
分数乘法
解决问题
分数乘整数
分数乘分数
分数乘小数
乘法运算律推广到分数
意义与计算方法
计算分数乘法,能约分的先约分
简便计算
求一个数的几分之几是
多少的问题
稍微复杂的求一个数的
几分之几是多少的问题
单位“1”的量×所求的量是单位“1”的几分之几=所求的量
一个整数乘分数有时表示几
个相同的分数相加,有时表
示这个整数的几分 之几。
能约分的,先约分
再算比较简便。
分数乘分数,用分子
乘分子,分母……
一个数的几分之几
都可用这个数乘上
几分之几表示。
一个数乘分数可以表示什么意思?怎样计算分数乘法?
一、比较每组题结果的大小,你发现了什么?
7
8
×
5
14
7
8
×
1
7
8
×
4
3
7
10
×
5
3
×
5
3
6
5
×
5
3
1
5
16
=
7
8
=
7
6
=
7
6
=
5
3
=
2
=
(1)
(2)
第二个因数>1,积>第一个因数;
第二个因数<1,积<第一个因数;
第二个因数=1,积=第一个因数。
二,判断。
1.a除以b的商是 ,那么a就占它们和的 。 ( )
2. 5m的 和5个 m一样长。 ( )
3.一个数乘真分数,所得的积一定小于这个数。 ( )
4.某景区门票价先提价 ,后降价 ,门票的价格不变。
( )
5. 水的质量比糖多 ,糖就比水少 。 ( )
2
1
3
1
3
1
3
1
1
10
1
10
5
1
4
1
√
×
√
×
×
三、简便计算下面各题
=18× -18×
9
5
6
1
=7
= ×4×5+ ×4×5
4
1
5
1
=9
= ×(1- )
5
2
3
1
=
15
4
= ×47+ ×1
47
6
47
6
=6
47
6
= ×( + )
7
5
4
1
4
3
=
7
5
= × ×
5
3
9
5
7
2
=
21
2
四、某修路队计划一条长为2.4千米的路。修了8天后,已修的比全长的 少1千米,已修了多少千米?
8
5
解:2.4× -1
=0.5(千米)
答:已修了0.5千米。
8
5
五、图书馆有600本文艺术,科技书是文艺书的 ,故事书是科技书的 ,故事书有多少本?
解:50× ×2=20(本)
50-20=30(本)
答:故事书有30本。
5
1
5
4
3
2
第 1 课时 分数乘法的意义(1)
第 1 单 元 分 数 乘 法
一、复习导入
(1)5个12是多少?
(2)
5×12=60
1.计算下列各题。
1
6
+
2
6
3
6
+
=
1
(3)
3
10
+
+
=
9
10
3
10
3
10
二、探究新知
1
小新、爸爸、妈妈一起吃一个蛋糕,每人吃 个,3人一共吃了多少个?
2
9
1.梳理信息,分析思路
问题:(1) 你知道了什么?
(2) 你能试着用图表示出题意吗?
二、探究新知
?个
2.画图分析
1
小新、爸爸、妈妈一起吃一个蛋糕,每人吃 个,3人一共吃了多少个?
2
9
二、探究新知
2
9
+
2
9
+
2
9
=
6
9
2
3
(个)
=
3.探究分数乘整数的意义
(1)求3个 是多少可以怎样列式?
9
2
(2)还可以怎样列式?
3个 相加,用乘法表示就是 ×3或 3× 。
2
9
2
9
2
9
分数乘整数的意义和整数乘法的意义相同,就是求几个相同加数的和的简便计算
二、探究新知
2
9
2×3
9
×3
6
9
(个)
=
=
2
9
+
2
9
+
2
9
=
2+2+2
9
=
4.探究分数乘整数的计算方法
分子相乘
分母不变
二、探究新知
2
9
2×3
9
×3
6
9
(个)
=
=
2
9
+
2
9
+
2
9
=
2+2+2
9
=
4.探究分数乘整数的计算方法
研讨问题:乘得的积是不是最简分数?应该怎么办?
分子相乘
分母不变
二、探究新知
2
9
2×3
9
×3
6
9
(个)
=
=
2
9
+
2
9
+
2
9
=
2+2+2
9
=
4.探究分数乘整数的计算方法
研讨问题:乘得的积是不是最简分数?应该怎么办?
9
2×3
=
9
6
2
9
×3
=
分子相乘
分母不变
2
3
=
3
2
(个)
二、探究新知
2
9
2×3
9
×3
6
9
(个)
=
=
2
9
+
2
9
+
2
9
=
2+2+2
9
=
4.探究分数乘整数的计算方法
研讨问题:乘得的积是不是最简分数?应该怎么办?
9
2×3
=
9
6
2
3
=
3
2
(个)
2×3
9
2
3
1
3
2
9
×3
=
(个)
=
2
9
×3
=
分子相乘
分母不变
观察比较以上两种约分的过程有什么不同,你喜欢哪个?说说想法。
二、探究新知
2.能先约分的可以先约分,再计算,结果相同。
1.分数乘整数,用分子乘整数的积作分子,分母
不变。
分数与整数相乘,
是怎样计算的?
5.讨论总结
三、巩固练习
1. 把下面的加法改写成乘法算式并计算。
×5 =
9
2
9
10
×4 =
10
3
5
6
×4 =
7
1
7
4
5个2是多少?
5×2=10
三、巩固练习
3袋重?kg
问题:1. 你知道了什么?
2. 解决“3袋重多少千克”这个问题, 请你列出算
式并计算。
或:3×
10
3
10
9
=
2.一袋面包重 kg。
3
10
×
=
3
10
3
10
9
三、巩固练习
3.直接说出得数。
问题:直接说出得数,并说说你是怎样想的。
=0
×4
15
2
×8
12
5
×4
9
2
×1
7
2
×0
3
2
2×
4
3
15
8
=
=
3
10
=
2
3
=
7
2
=
9
8
四、作业布置
作业:第6页练习一,
第1题、第2题、第3题。
六年级数学上册(RJ) 教学课件
第 2 课时 分数乘法的意义(2)
第 1 单 元 分 数 乘 法
一、复习导入
1.计算下面各题。
说说计
算方法。
3
7
2
×
1
10
3
×
3
15
5
×
6
7
3
10
3
5
=
=
=
2.说说分数乘整数的意义是什么。
二、探究新知
1桶水有12L。
3桶共多少升?
1.你知道了什么?
2.要求“3桶水共重多少升”
怎样列式?
(求3个12L,就是求12L的3倍是多少。)
2
1.出示问题
12×3
你是怎么
想的?
二、探究新知
桶是多少升?
1
2
问题:1.你知道了什么?
3.你是根据什么列式的?
表示求半桶水的体积,就是求12L
的一半,也就是求12L的 是多少。
2.要求“ 桶是多少升?”怎样列式?
1
2
1
12
×
每桶的体积×桶数=总体积
1
2
12
×
( )
( )
2
12
二、探究新知
桶是多少升?
1
4
1
4
12
×
问题:1.你知道了什么?
2.要求“ 桶是多少升?”怎样列式?
3.你是根据什么列式的?
1
4
每桶的体积×桶数=总体积
4. 表示求 桶水的体积,就是求12L的 。
1
4
12
×
1
4
( )
( )
1
4
二、探究新知
桶是多少升?
1
2
12
×
12
桶是多少升?
1
4
1
4
12
×
观察比较上面两个算式表示的意思有什么相同之处?
2.讨论总结
小结:一个数乘几分之几表示的是求这个数的几分之几是多少。
三、巩固新知
2.要求吃了多少千克,请你列出算式。
3.你是根据什么列出算式的?
一袋面粉重3kg。已经吃了它的 ,吃了多少千克?
3
10
×
(把一袋面粉平均分成10份,吃了的占3份。)
问题:1.你是怎样理解“已经吃了它的 ”这句话的?
3
10
(求3kg的 是多少。)
3
10
3
3
10
四、巩固练习
一个数(0除外)乘一个小于1的数,积小于这个数;乘一个大于的数,积大于这个数;乘1,积等于这个数。
<
>
=
判断大小,寻找规律
六年级数学上册(RJ) 教学课件
第 3 课时 分数乘分数(1)
第 1 单 元 分 数 乘 法
一、引入情景 探究新知
3
1
2
李伯伯家有一块 公顷的地。
种土豆的面积占这块地的 ,
种玉米的面积占 。
5
1
5
3
一、引入情景 探究新知
3
1
2
李伯伯家有一块 公顷的地。
种土豆的面积占这块地的 ,
种玉米的面积占 。
5
1
5
3
(1)种土豆的面积是多少公顷?
(2)种玉米的面积是多少公顷?
一、引入情景 探究新知
1.明确问题 提取信息
解决问题(1)种土豆的面积是多少公顷?
问题:1. 题目中的已知条件是什么?
5
1
2. 你是怎样理解“种土豆的面积占这块地的 ”这句话的意思的?
(把这块地平均分成5份,种土豆的面积占1份。)
1
5
占
1
2
公顷
一、引入情景 探究新知
2.分析题意,列式计算
2
1
5
1
2
1
5
1
×
求 公顷的 是多少,可以用乘法计算,列式为 。
(1)实践操作
3.探究计算方法
1
2
公顷
公顷的
1
5
1
2
1
2
×
1
5
1×1
2×5
1
10
(公顷)
=
=
1公顷
平均分成2份,
每份是 公顷
1
2
将 公顷平均
分成 5 份,
1
2
其中的1份占
1公顷的
1
10
1公顷的 即 公顷
1
10
1
10
(2)列式计算
一、引入情景 探究新知
解决问题(2)种玉米的面积是多少公顷?
1. 你是怎样理解“种玉米的面积占 ”这句话?
5
3
2. 怎样列式呢?
(把这块 地平均分成5份,种玉米的面积占3份。)
2
1
5
3
2
1
5
3
×
(求 公顷的 是多少,可以用 表示。)
一、引入情景 探究新知
3. 请你用一张纸动手折一折、画一画,用阴影表示出 的意思。
2
1
5
3
×
公顷
10
3
1
2
公顷
公顷的
3
5
1
2
公顷的 ,就是把 公顷平均分成5份,取其中的3份,也就是把1公顷平均分成(2×5)份,取其中的3份,平均分成(2×5)份,“取其中的3份”就乘“3”,用算式表示是
1
2
3
5
1
2
2×5
1
×3=
2×5
1×3
1
2
×
3
5
=
×
×
(公顷)
2
5
1
10
3
3
=
二、课堂小结
讨论:分数乘分数怎样计算?
用分母相乘的积作分母。
分数乘分数,用分子
相乘的积作分子。
三、巩固练习
(1) kg的 是多少千克?
×
(2) kg的 是多少千克?
1.只列式,不计算。
5
3
2
1
7
4
12
7
×
2
1
5
3
12
7
7
4
三、巩固练习
2.看图计算。(教材P5T2)
2
1
2
1
×
=
( )
( )
3
2
5
4
×
=
( )
( )
4
3
4
3
×
=
( )
( )
4
1
15
8
16
9
六年级数学上册(RJ) 教学课件
第 4 课时 分数乘分数(2)
第 1 单 元 分 数 乘 法
一、复习导入
1.口算下列各题。
3
8
4
×
2
5
5
×
1
10
2
×
3
2
2
1
5
=
=
=
1
6
5
×
3
23
8
×
3
7
2
×
3
2
24
23
6
7
=
=
=
一、复习导入
2.计算下列各题。
3
4
×
2
3
=
8
9
1
2
×
3
7
=
6
7
5
8
×
5
14
=
4
7
5
24
×
5
27
=
8
9
8
25
×
4
15
=
5
6
二、探究新知
9
10
(1)李叔叔的游泳速度是乌贼的 。李叔叔每分钟游多少千米?
4
45
4
无脊椎动物中游泳最快的是乌贼,
它的速度是 千米/分。
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A} 已知条件
所求问题
乌贼每分钟游 km
李叔叔每分钟游多少千米?
李叔叔每分钟游的距离是乌贼的
理解题意
9
10
4
45
二、探究新知
2.你是怎样理解“李叔叔的游泳速度是乌贼的 这句话的?
4
45
(把乌贼的速度平均分成45份,李叔叔的游泳速度有这样的4份。)
9
10
×
4
45
9×4
10×45
2
25
(km)
=
=
1
\
\
\
\
5
2
5
为了计算简便,可
以先约分再乘。
解法探究
二、探究新知
(2)乌贼30分钟可以游多少千米?
理解题意
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}已知条件
所求问题
速度
时间
路程
乌贼的游泳速度是 千米/分
30分钟
30分钟可以游多少千米
9
10
二、探究新知
1.要求乌贼30分钟可以游多少千米,怎样列式?
2.请你独立计算。
研讨问题:方法2和方法3
的约分方法你更喜欢哪个?
预设1:
10
9
×30=
10
9×30
=
10
270
预设2:
10
9
×30=
10
9×30
=
10
270
=27
27
1
预设3:
10
9
×30=
=27
10
9
×30
1
3
研讨问题:这个结果是不
是最简分数?
10
9
×30
(km)
(km)
(km)
解法探究
二、探究新知
小结:分数乘分数,用分子相乘的积作分子,用分母相乘的积作分母。
为了计算简便,可以先约分再乘。
你觉得分数乘法该怎样计算呢?
三、巩固练习
1.计算下面各题。
7
3
×21
7
16
×
48
35
11
19
×
38
33
11
9
×121
21
17
×
68
63
9
5
×
3
10
= 9
= 99
=
5
3
=
3
2
=
3
4
=
50
27
三、巩固练习
一个数(0除外)乘一个小于1的数,积小于这个数;乘一个大于的数,积大于这个数;乘1,积等于这个数。
<
>
=
2.判断大小,寻找规律
三、巩固练习
3. 蜂鸟是目前所发现的世界最小的鸟,也是唯一能倒飞的鸟。蜂鸟的飞行速度是 千米/分,
分钟飞行多少千米?5分钟飞行多少千米?
3
10
3
2
解: × = (千米) ×5 = (千米)
答: 分钟飞行 千米,5分钟飞行 千米。
3
2
10
3
10
3
5
1
2
3
3
2
5
1
2
3
三、巩固练习
4.下面是园林处三位职工铺草坪的情况
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}姓名
王伟
李红
徐光
每小时铺的面积/平方米
6
铺的时间/时
4
3
5
27
3
4
2
15
5
6
他们分别铺了多少平方米?
思路分析:每小时铺的面积是工作效率,铺的时间是工作时间,铺了的面积是工作总量。根据工作效率×工作时间=工作总量可分别列式解答。王伟的工作效率是每小时铺6平方米,工作时间是 ,求工作总量,列式为 。李红和徐光的工作总量的求法相同。
4
3
解答:
王伟:6 × = (平方米)
李红: × = (平方米)
徐光: × = 9(平方米)
4
3
2
9
3
2
36
5
6
2
15
4
5
27
四、拓展训练
a、b是不为0的整数,a×
3
b
5
b
思路分析:由一个不为0的数乘小于1的数,得数小于他本身,可知a×
5
b
5
b
3
b
3
b
六年级数学上册(RJ) 教学课件
第 5 课时 分 数 乘 小 数
第 1 单元 分数乘法
1.求下面各题的商。(分别用小数、分数表示)
一、复习导入
5÷10= 9÷100=
37÷1000= 2÷10=
20÷100= 50÷1000=
0.5=
1
2
0.09=
9
100
0.037=
37
1000
0.2=
1
5
0.2=
1
5
0.05=
1
20
我身体长2.1dm。
欢欢
二、探究新知
可以把2.1化成分数,
也可以把 化成小数。
(1)松鼠欢欢的尾巴有多长?
松鼠的尾巴长度约占身体长度的 。
3
4
3
4
×
=
3
4
2.1
(dm)
1.575
0.75
5
我身体长2.4dm。
松鼠的尾巴长度约占身体长度的 。
3
4
(2)松鼠乐乐的尾巴有多长?
×
=
3
4
2.4
×
3
4
2.4
\
\
=
1.8(dm)
0.6
1
这样约分计
算真简便。
你是怎样计算的?和同学交流一下你的方法。
小结:在计算小数乘分数时 ,可以把小数化成分数,可以把分数化成小数,也可以直接约分计算。要注意在计算时能约分的要先约分。
三、课堂小结
四、巩固练习
3
5
3
5
5
6
5
6
1.2× =
2.5× =
1.4× =
2.4× =
18
25
3
2
7
6
2
四、巩固练习
=
=
=
=
=
=
12
25
27
25
161
40
381
70
18
5
2
75
六年级数学上册(RJ) 教学课件
第 6 课时 分数混合运算
第 1 单元 分数乘法
1.计算下面各题。
一、复习导入
15×(34-29)=
16×4-7×9=
70-4×6=
75
1
46
2.用简便方法计算下面各题。
2.5×98×0.4 1.25×2.5×8×4
=98
(8+0.8)×12.5
=110
=100
1
2
m
4
5
m
二、探究新知
预设1:
5
4
( + )×2
2
1
预设2:
5
4
×2+ ×2
2
1
问题:1. 分数混合运算的顺序和整数混合运算的顺序相同,
你会自己计算上面这两道算式吗?
2. 通过计算你有什么发现?
5
4
( + )×2=
2
1
5
4
×2+ ×2
2
1
6
一个画框的尺寸如右图,做这个画框需要多长的木条?
观察每组的两个算式,看看它们有什么关系。
×
3
1
2
1
×
2
1
3
1
4
1
( × )×
3
2
5
3
4
1
×( × )
3
2
5
3
2
1
( + )×
3
1
5
1
2
1
× + ×
3
1
5
1
5
1
=
=
=
小结:整数乘法的交换律、结合律和分配律,对于
分数乘法也适用。
从这些算式中,你发现了什么规律?
三、课堂小结
1.商店运来一些水果,运来苹果20筐,梨的筐数是苹果的 ,同时橘子的筐数又是梨的 。运来橘子多少筐?
4
3
5
3
解:20× ×
= 20×( × )= 9(筐)
答:运来的橘子有9筐。
3
5
3
4
3
4
3
5
四、巩固训练
2.超市购进一批酸奶共30盒,每盒有8杯,每杯酸奶 升,
这批酸奶一共有多少升?
4
15
解:30×8×
=64(升)
答:这批酸奶一共有64升。
15
4
六年级数学上册(RJ) 教学课件
第 7 课时 分数简便运算
第 1 单元 分数乘法
一、复习导入
= ×4×5+ ×4×5
4
1
5
1
=9
= ×( + )
7
5
4
1
4
3
=
7
5
计算。
二、探究新知
研讨问题:你运用了什么运算定律?(乘法交换律和乘法结合律。)
研讨问题:你是怎样想的?(先做小括号里的,再做括号外的。)
问题:请你先独立计算上面两道题。
预设1:
5
3
×( ×5)=
6
1
×
6
5
5
3
=
2
1
1
1
1
2
1
预设2:
( ×5) × =
5
3
6
1
=
5
3
×( ×5)=
6
1
2
1
1
×
6
1
3
1
2
6
5
( + )×12
4
1
5
3
×( ×5)
6
1
7
研讨问题:你运用了什么运算定律?(运用乘法分配律,计算简便。)
小结:整数乘法的交换律、结合律和分配律,对于分数乘法也适用。
应用乘法的运算定律,可以使一些计算简便。
研讨问题:你是怎样想的?(先做小括号里的,再做括号外的。)
观察这2种计算方法,你喜欢哪种方法?说说你的想法。
6
5
( + )×12
4
1
预设1:
( + )×12
6
5
( + )×12
4
1
=
12
10
12
3
12
13
= ×12=13
1
1
=
预设2:
×12 + ×12
6
5
( + )×12
4
1
=10+3=13
6
5
4
1
2
1
3
1
三、课堂小结
从这些算式中,你发现了什么规律?
小结:分数混合运算时,要善于结合数据特点,灵活运用乘法的运算定律,使计算更简便。
×27+
9
8
27
×27
=
3
2
× ×3
4
=
1. 用简便方法计算下面各题,并说一说运用了什么运算定律。
3
2
× ×3
4
1
( + )×27
9
8
27
4
=(1+86)×
86
3
2
1
1
1
1
2
1
=
=24+4
=28
4
=
86
3
+3
=3
86
3
1× +86×
86
3
86
3
=
87×
86
3
四、巩固练习
四、巩固练习
2. 奶牛场每头奶牛平均日产牛奶 t,42头奶牛100天可产奶多少吨?
50
1
×42×100
50
1
×42×100
50
1
2
1
= 84(t)
=
六年级数学上册(RJ) 教学课件
第 8 课时 解 决 问 题(1)
第 1 单元 分数乘法
(4)母鸡的只数相当于公鸡的 。
(1)乙数是甲数的 。
(2)乙数的 相当于甲数。
(3)母鸡只数 等于小鸡的只数。
1
3
4
5
1
3
4
5
下面各题分别把谁看作单位“1”?
一、复习导入
其中一半种各种萝卜。红萝卜地的面积占整块萝卜地的 。
1
4
大棚共480m2
二、探究新知
红萝卜地有多少平方米?
8
理解题意
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
已知条件
整个大棚的面积是 480m2 。
萝卜地的面积占整个大棚面积的 。
红萝卜地的面积占萝卜地面积的 。
所求问题
红萝卜地的面积是多少平方米。
2
1
4
1
(1)怎样理解“其中的一半种各种萝卜”?
(2)怎样理解“红萝卜地的面积占整块萝卜地的 ”?
4
1
红萝卜地有多少平方米?
(把这块地平均分成2份,其中1份种各种萝卜)
(把种各种萝卜的面积平均分成4份,红萝卜占其中的1份。)
分析与解答
其中一半种各种萝卜。红萝卜地的面积占整块萝卜地的 。
1
4
大棚共480m2
8
方法探究
红萝卜地有多少平方米?
480m2
红萝卜地占萝卜地面积的
1
4
各种萝卜地占大棚面积的
1
2
(3)你能用示意图表示出题目的意思吗?
(4)请你解答这道题。
研讨问题:请你结合图说说你是怎样想的。
(先求出萝卜地的面积,再求出红萝卜地的面积。)
两种方法虽然不同,可以用一个综合算式表示:
480× × =60(m2)
2
1
预设1:
2
1
480× =240(m2)
4
1
240× =60(m2)
预设2:
×
4
1
2
1
=
8
1
8
1
480× =60(m2)
4
1
分析与解答
刚才用两种方法求出了红萝卜的面积,那么对不对呢?都可以怎样检验?
研讨问题:请你结合图说说你检验的思路。
(红萝卜的面积乘4表示萝卜地的面积,再乘2就是大棚的面积)
研讨问题:请你结合图说说你检验的思路。
(把大棚面积平均分成8份,红萝卜地占1份,用1份的面积
乘8就是大棚的面积。)
预设1:
60×4×2=480( )
预设2:
60×(4×2)=480( )
回顾与反思
回顾与反思
规范解答
解:480× × =60(m2)
答:红萝卜地有60m2。
2
1
2
1
分析与解答
其中一半种各种萝卜。红萝卜地的面积占整块萝卜地的 。
1
4
大棚共480m2
8
红萝卜地有多少平方米?
三、巩固练习
小亮的储蓄箱中有18元,小华储蓄的钱是小亮的 ,小新储蓄的钱是小华的 。小新储蓄了多少元?
6
5
3
2
解:18× × =10(筐)
答:小新储蓄了10元。
5
6
2
3
四、课堂小结
通过前面的学习,你有什么发现吗?
1.求一个数的几分之几是多少,属于两个量相比的关系。用线段图可以比较清楚地表示出数量之间的关系:
单位“1”的量×比较量占单位“1”的几分之几=比较量
2.解决连续求一个数的几分之几是多少的实际问题,弄清每一步单位“1”的量是谁最关键的。
六年级数学上册(RJ) 教学课件
第 9 课时 解 决 问 题(2)
第 1 单元 分数乘法
一、情境导入,探究新知
人心脏跳动的次数随年龄而变化。青少年心跳每分钟约75次,婴儿每分钟心跳的次数比青少年多 。婴儿每分钟心跳多少次?
5
4
9
理解题意
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
已知条件
青少年每分钟心跳约75次。
婴儿每分钟心跳的次数比青少年多 ,多的部分是婴儿的。
所求问题
婴儿每分钟心跳的次数。
5
4
(2)这道题怎样解答,请你根据题意先画出线段图。
(1)怎样理解“婴儿每分钟心跳的次数比青少年多 ”?
婴儿每分钟心跳次数与青少年心跳次数相比较,把青少
年每分钟心跳次数看作单位“1”;多的部分是青少年心
跳次数的 ,婴儿每分钟心跳次数是(1+ )。
5
4
5
4
5
4
分析与解答
解法探究
青少年:
婴儿:
?次
75次
比青少年多
4
5
分析与解答
研讨问题:请你结合图说说你是怎样想的。
求婴儿每分钟心跳次数就是求青少年的(1+ )是多少。
研讨问题:请你结合图说说你是怎样想的。(先求出婴儿比青少年多的,再
加上青少年每分钟心跳的次数,就是婴儿每分钟心跳的次数。)
预设1:
75+75× =75+60=135(次)
5
4
预设2:
75×(1+ )=75× =135(次)
5
4
5
9
5
4
回顾与反思
问题:1. 两种解题思路有什么不同?
2. 刚才用两种方法求出了婴儿的每分钟心跳次数,那么对不对呢?
可以怎样检验?
(135-75)÷75
75+75× =75+60=135(次)
5
4
5
9
5
4
75×(1+ )=75× =135(次)
5
4
青少年:
婴儿:
135次
75次
比青少年多?
= 60 ÷ 75
=
回顾与反思
小结:虽然两种解法不同,但都是依据了分数乘法的意义解决稍复杂的求一个数的几分之几是多少的问题。
75+75× =75+60=135(次)
5
4
规范解答
答:婴儿每分钟135。
二、课堂小结
“已知一个数比另一个数多几分之几,求这个数”的解题方法有两种:
(1)单位“1”的量+单位“1”的量×比单位“1”多的几分之几=所求的量
(2)单位“1”的量×(1+比单位“1”多的几分之几)=所求的量
三、巩固练习
1.一袋大米重25千克,先吃去这袋大米的 ,又吃去剩下的 千克,两次一共吃去多少千克?
5
1
5
1
解:25× =5(千克)
25× × =1(千克)
5+1=6(千克)
答:两个一共吃去了6千克。
1
5
1
5
1
5
2.一台笔记本电脑,先降价 ,后来又提价 。现价与原价相比是升了还是降了?
9
1
9
1
解:假设原价为“1”,那么现价为:
1×(1- )×(1 + )
=
因为 <1,所以现价与原价相比降了
答:现价与原价相比降了。
9
1
9
1
81
80
81
80
六年级数学上册(RJ) 教学课件
第 10 课时 整 理 和 复 习
第 1 单元 分数乘法
分数乘法
分数乘法
解决问题
分数乘整数
分数乘分数
分数乘小数
乘法运算律推广到分数
意义与计算方法
计算分数乘法,能约分的先约分
简便计算
求一个数的几分之几是
多少的问题
稍微复杂的求一个数的
几分之几是多少的问题
单位“1”的量×所求的量是单位“1”的几分之几=所求的量
一个整数乘分数有时表示几
个相同的分数相加,有时表
示这个整数的几分 之几。
能约分的,先约分
再算比较简便。
分数乘分数,用分子
乘分子,分母……
一个数的几分之几
都可用这个数乘上
几分之几表示。
一个数乘分数可以表示什么意思?怎样计算分数乘法?
一、比较每组题结果的大小,你发现了什么?
7
8
×
5
14
7
8
×
1
7
8
×
4
3
7
10
×
5
3
×
5
3
6
5
×
5
3
1
5
16
=
7
8
=
7
6
=
7
6
=
5
3
=
2
=
(1)
(2)
第二个因数>1,积>第一个因数;
第二个因数<1,积<第一个因数;
第二个因数=1,积=第一个因数。
二,判断。
1.a除以b的商是 ,那么a就占它们和的 。 ( )
2. 5m的 和5个 m一样长。 ( )
3.一个数乘真分数,所得的积一定小于这个数。 ( )
4.某景区门票价先提价 ,后降价 ,门票的价格不变。
( )
5. 水的质量比糖多 ,糖就比水少 。 ( )
2
1
3
1
3
1
3
1
1
10
1
10
5
1
4
1
√
×
√
×
×
三、简便计算下面各题
=18× -18×
9
5
6
1
=7
= ×4×5+ ×4×5
4
1
5
1
=9
= ×(1- )
5
2
3
1
=
15
4
= ×47+ ×1
47
6
47
6
=6
47
6
= ×( + )
7
5
4
1
4
3
=
7
5
= × ×
5
3
9
5
7
2
=
21
2
四、某修路队计划一条长为2.4千米的路。修了8天后,已修的比全长的 少1千米,已修了多少千米?
8
5
解:2.4× -1
=0.5(千米)
答:已修了0.5千米。
8
5
五、图书馆有600本文艺术,科技书是文艺书的 ,故事书是科技书的 ,故事书有多少本?
解:50× ×2=20(本)
50-20=30(本)
答:故事书有30本。
5
1
5
4
3
2
