人教版(2019)高一物理 必修 第二册 第五章:5.4抛体运动的规律(共46张PPT)
文档属性
| 名称 | 人教版(2019)高一物理 必修 第二册 第五章:5.4抛体运动的规律(共46张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 3.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-08-23 06:09:35 | ||
图片预览









文档简介
(共46张PPT)
抛体运动的规律
飞机扔下的炸弹
瀑布留下的水流
姚明投出的篮球
赛场上扔出的铅球
抛体运动
1.
定义:以一定的初速度将物体抛
出,在空气阻力可以忽略的情况下,物
体只受重力作用的运动。
踢出的足球
抛体运动
1.
定义:以一定的初速度将物体抛出,在空气阻力可以忽略的情况下,物体只受重力作用的运动。
2.
分类:
平
抛
斜向上抛
斜向下抛
3.受力特征
4.运动特征
5.运动轨迹
3.受力特征:只受重力
4.运动特征:加速度为g,所以是匀变速运动
5.运动轨迹:加速度与初速度不共线,物体做匀变速曲线运动
1.
定义:水平抛出且只受重力作用的
物体的运动。
一、平抛运动
1.
定义:水平抛出且只受重力作用的
物体的运动。
一、平抛运动
2.
条件:①有水平初速度
②只受重力
1.
定义:水平抛出且只受重力作用的
物体的运动。
一、平抛运动
2.
条件:①有水平初速度
②只受重力
3.
运动性质:平抛运动是一种匀变速曲
线运动。
二、对平抛运动的研究
平抛运动研究方法
将其分解为两个方向的运动
研究方法:
化曲为直
轨迹是曲线
采用运动的合成和分解
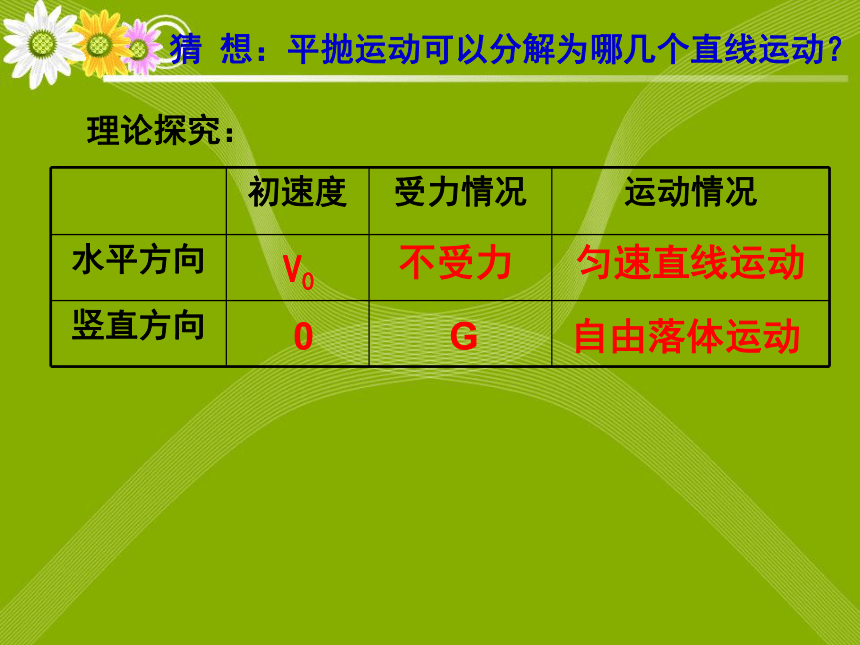
猜
想:平抛运动可以分解为哪几个直线运动?
理论探究:
0
G
自由落体运动
初速度
受力情况
运动情况
水平方向
竖直方向
V0
不受力
匀速直线运动
v0
G
FN
v0
G
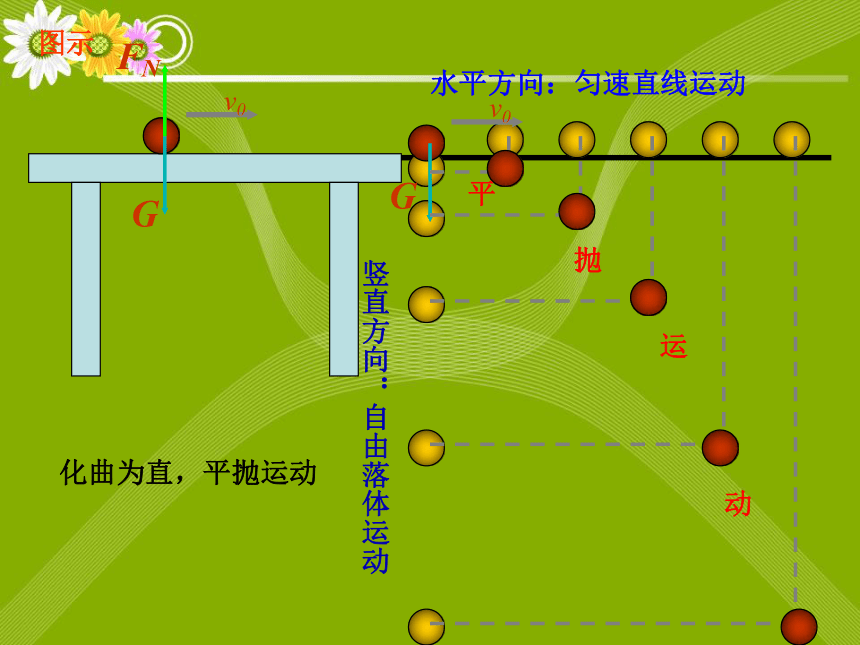
竖直方向:自由落体运动
水平方向:匀速直线运动
平
抛
运
动
化曲为直,平抛运动
图示
竖直方向的自由落体运动.
结论:平抛运动可以分解为
水平方向的匀速直线运动.
平抛运动是水平方向的匀
速直线运动与竖直方向的自由落
体运动的合运动.
三、平抛运动的规律
以抛出点为坐标原点;初速度v0的方向为x
轴的正方向;竖直向下的方向为y
轴正方向
研究的问题是:
1、加速度
2、速度
3、位移
4、轨迹方程
v0
x
y
1、平抛物体的加速度
水平方向:
竖直方向:
加速度的方向:
竖直向下
2、平抛物体在某时刻的瞬时速度
水平方向:
竖直方向:
合速度大小:
VO
mg
o
x
y
vx
vy
v
t
θ
tanθ=
速度方向:
3、平抛物体在某时刻的位移:
合位移大小:
水平方向:
竖直方向:
位移方向:
o
x
y
s2
s1
s
t
?
tanα=
4.平抛运动的轨迹:
0
x
y
v0
思考:
平抛运动的速度与水平方向
的夹角和位移与水平方向的夹角
相同吗?
x
y
s
?
?
tanθ=
tanα=
?
)
)
)
2tanα
tanθ=
x
v0
Vx
Vy
O
A
B
O’
推论1
平抛物体任意时刻瞬时时速度方向的反向延长线与初速度延长线的交点到抛出点的距离都等于水平位移的一半。
v0
vt
vx
vy
h
s
α
α
s/
证明:设时间t
内物体的水平位移为s,竖直位移为h,
则末速度的水平分量vx=v0=s/t,
而竖直分量vy=2h/t,
所以有
推论2
重要推论
(1)飞行时间:
(2)水平射程:
(3)落地速度:
飞行时间只由高度决定
(4)
tan
q
=
tan
2
位移偏角与速度偏角不相等
(5)
AB=OB/2
O
x
y
P
(x,y)
B
B
A
α
解平抛运动类问题的一般思维:
1.分解速度:根据速度中合速度和分速度的方向(角度)和大小关系进行求解
2.分解位移:根据位移中分运动和合运动的大小和方向(角度)关系进行求解
题型:基本规律的应用
斜面上的抛体运动
类平抛运动
小结
一.平抛运动
1.定义:将物体以一定的初速度沿水平方向抛出,物体只在
重力作用下所做的运动。
2.条件:有一定的水平初速度;只受重力的作用(忽略空气阻力)
3.特点:①
有水平初速度
②
只受重力作用
③
a=g
④
匀变速曲线运动
二、运动规律:
水平方向:
匀速直线运动.
在竖直方向:自由落体运动.
三、公式:
1.加速度
2.速度
3.位移
求解常见思路:化曲线运动为直线运动
平抛运动基本规律
①
加速度:
水平方向:合外力为0,a=0
竖直方向:合外力为G,a=g
合运动:a=g、方向竖直向下
②速度:
合速度
方向
:tanθ=
③位移:
x=vot
y=
合位移:s=
方向:
tanα=
tanθ
=2tanα
a、运动时间和射程:水平方向和竖直方向的两个分运动既具有独立性,又具有等时性.
所以运动时间为
即运动时间由高度h惟一决定
b、水平射程为
即由v0、h共同决定
c、合速度
④结论总结
d、速度的变化量
g=△v/△t,
△t时间内速度改变量相等,
即△v=g△t,
△v方向是竖直向下的.
例1、一水平匀速飞行的飞机上丢下一炸弹,问在地面上的人看来,它们作什么运动?在飞行员看来,这颗炸弹作什么运动?
答:(1)地面上的人看到炸弹作平抛运动。因炸弹离开飞机时由于惯性具有与飞机飞行速度相同的水平初速度,且炸弹只在重力作用下运动,所以是平抛运动。
(2)飞行员看到炸弹作自由落体运动。因炸弹与飞机具有相同的水平速度,相对初速度为零,炸弹在重力作用下远离飞机,所以是自由落体运动。
例2、如图,树枝上的一只松鼠看到一个猎人正用枪对准它,为了逃脱即将来临的厄运,它想让自己落到地面上逃走。但是就在它掉离树枝的瞬间子弹恰好射出枪口,问松鼠能逃脱厄运吗?
答:不能。因子弹和松鼠在竖直方向都是自由落体运动,竖直方向的位移总是相同的,所以只要在子弹的射程内,就一定能射中松鼠,松鼠在劫难逃。
我闪!!!
哪里逃?
这样也能打中!
例3、在水平路上行驶的汽车,遇到一个壕沟,汽车的速度至少为多大,才能越过这个壕沟?
(g=10m/s2)
25米
5米
【答案】
例4、如图所示,在倾角为370的斜面底端的正上方H处,平抛一小球,该小球垂直打在斜面上的一点,试求小球抛出时的初速度和飞行时间。
H
v0
370
解:画出示意图
由平抛运动规律X=Vo
t
Y=(1/2)gt?
由几何关系得:
(H-
Y)/
X=tan
370
H
v0
370
Vx
Vy
tan530=
分解位移:根据位移中分运动和合运动的大小和方向(角度)关系进行求解
例5、如图所示,A、B两球间用长6m的细线相连,两球相隔0.8s先后从同一高度处以4.5m/s的初速度平抛,则A球抛出几秒后A、B
间的细线被拉直?在这段时间内A球的位移是多大?不计空气阻力,g=10m/s2。
B
A
B
′
A′
B
A
B
′
A′
解:由平抛运动规律可得
:
xA=v0
t
yA=1/2×g
t
2
xB
=v0
(t-0.8)
yB=1/2×g(t-0.8)
2
l
2
=(xA-xB)
2
+(yA-yB)
2
代入数字得
36
=(4.5×0.8)
2
+1/2×10×
(1.6t-0.64)
解得
t=1s
xA=v0
t=4.5m
yA=1/2×g
t
2=5m
sA
2
=xA
2
+yA
2=4.5
2
+5
2
=45.25
sA
=6.73m
例6、已知排球场半场长L,网高H,如图示,若队员在离网水平
距离d
处竖直跳起水平扣球时,不论以多大的速度击球,都不能把球击在对方场地内,则队员应在离地多高处击球?
h
H
d
v
L
h
H
d
v
L
解:设高度为h,当运动员用速度v1扣球时,球刚好压边线,
用速度v2扣球时,球刚好触网,
若v1
=
v2
=
v,则既触网又压边线
不能把球击在对方场地内,则
斜抛运动
1.
轨迹:(如图)
2.
水平速度:
水平位移:
3.
竖直速度:
竖直位移:
x=v0tcos?
vx=v0cos?
vy=v0sin?
-
gt
Hm
x
y
O
v0
特点:物体所受的合力为恒力,且与初速度的方向垂直(初速度的方向不一定是水平方向,合力的方向也不一定是竖直方向,加速度大小不一定等于重力加速度。)
处理方法:可看成某一方向的匀速直线运动和垂直此方向的匀加速直线运动的合运动。(处理类平抛运动的方法与处理平抛运动的方法类似,但要分清其加速度的大小和方向。)
类平抛运动
类平抛运动的求解方法
(1)常规分解法:将类平抛运动分解为沿初速度方向的匀速直线运动和垂直于初速度方向(即沿合力的方向)的匀加速直线运动,两分运动彼此独立,互不影响,且与合运动具有等时性.
(2)特殊分解法:对于有些问题,可以过抛出点建立适当的直角坐标系,将加速度分解为ax、ay,初速度v0分解为vx、vy,然后分别在x、y方向列方程求解.
例1、如图4-2-8所示,有一倾角为30°的光滑斜面,斜面长L为10
m,一小球从斜面顶端以10
m/s的速度在斜面上沿水平方向抛出.求:(g取10
m/s2)
(1)小球沿斜面滑到底端时的水平位移x.
(2)小球到达斜面底端时的速度大小.
答案:(1)20
m (2)14.1
m/s
例2、质量为m的飞机以水平速度v0,飞离跑道后逐渐上升,若飞机在此过程中水平速度保持不变,同时受到重力和竖直向上的恒定升力(该升力由其他力的合力提供,不含重力).今测得当飞机在水平方向的位移为l时,它的上升高度为h,如图所示,
求:(1)飞机受到的升力大小?
[思路点拨] 本题以曲线运动为背景,考查运动的合成与分解问题,解答的方法是将飞机的运动分解成水平和竖直两个方向上的直线运动.
归纳拓展:
(1)类平抛运动规律与平抛运动规律相同,处理方法也相同.平抛运动的两个重要推论也适用于类平抛运动.
(2)解答类平抛运动问题时,不一定按水平方向和竖直方向进行分解,可以按初速度方向和合外力方向来分解.
抛体运动的规律
飞机扔下的炸弹
瀑布留下的水流
姚明投出的篮球
赛场上扔出的铅球
抛体运动
1.
定义:以一定的初速度将物体抛
出,在空气阻力可以忽略的情况下,物
体只受重力作用的运动。
踢出的足球
抛体运动
1.
定义:以一定的初速度将物体抛出,在空气阻力可以忽略的情况下,物体只受重力作用的运动。
2.
分类:
平
抛
斜向上抛
斜向下抛
3.受力特征
4.运动特征
5.运动轨迹
3.受力特征:只受重力
4.运动特征:加速度为g,所以是匀变速运动
5.运动轨迹:加速度与初速度不共线,物体做匀变速曲线运动
1.
定义:水平抛出且只受重力作用的
物体的运动。
一、平抛运动
1.
定义:水平抛出且只受重力作用的
物体的运动。
一、平抛运动
2.
条件:①有水平初速度
②只受重力
1.
定义:水平抛出且只受重力作用的
物体的运动。
一、平抛运动
2.
条件:①有水平初速度
②只受重力
3.
运动性质:平抛运动是一种匀变速曲
线运动。
二、对平抛运动的研究
平抛运动研究方法
将其分解为两个方向的运动
研究方法:
化曲为直
轨迹是曲线
采用运动的合成和分解
猜
想:平抛运动可以分解为哪几个直线运动?
理论探究:
0
G
自由落体运动
初速度
受力情况
运动情况
水平方向
竖直方向
V0
不受力
匀速直线运动
v0
G
FN
v0
G
竖直方向:自由落体运动
水平方向:匀速直线运动
平
抛
运
动
化曲为直,平抛运动
图示
竖直方向的自由落体运动.
结论:平抛运动可以分解为
水平方向的匀速直线运动.
平抛运动是水平方向的匀
速直线运动与竖直方向的自由落
体运动的合运动.
三、平抛运动的规律
以抛出点为坐标原点;初速度v0的方向为x
轴的正方向;竖直向下的方向为y
轴正方向
研究的问题是:
1、加速度
2、速度
3、位移
4、轨迹方程
v0
x
y
1、平抛物体的加速度
水平方向:
竖直方向:
加速度的方向:
竖直向下
2、平抛物体在某时刻的瞬时速度
水平方向:
竖直方向:
合速度大小:
VO
mg
o
x
y
vx
vy
v
t
θ
tanθ=
速度方向:
3、平抛物体在某时刻的位移:
合位移大小:
水平方向:
竖直方向:
位移方向:
o
x
y
s2
s1
s
t
?
tanα=
4.平抛运动的轨迹:
0
x
y
v0
思考:
平抛运动的速度与水平方向
的夹角和位移与水平方向的夹角
相同吗?
x
y
s
?
?
tanθ=
tanα=
?
)
)
)
2tanα
tanθ=
x
v0
Vx
Vy
O
A
B
O’
推论1
平抛物体任意时刻瞬时时速度方向的反向延长线与初速度延长线的交点到抛出点的距离都等于水平位移的一半。
v0
vt
vx
vy
h
s
α
α
s/
证明:设时间t
内物体的水平位移为s,竖直位移为h,
则末速度的水平分量vx=v0=s/t,
而竖直分量vy=2h/t,
所以有
推论2
重要推论
(1)飞行时间:
(2)水平射程:
(3)落地速度:
飞行时间只由高度决定
(4)
tan
q
=
tan
2
位移偏角与速度偏角不相等
(5)
AB=OB/2
O
x
y
P
(x,y)
B
B
A
α
解平抛运动类问题的一般思维:
1.分解速度:根据速度中合速度和分速度的方向(角度)和大小关系进行求解
2.分解位移:根据位移中分运动和合运动的大小和方向(角度)关系进行求解
题型:基本规律的应用
斜面上的抛体运动
类平抛运动
小结
一.平抛运动
1.定义:将物体以一定的初速度沿水平方向抛出,物体只在
重力作用下所做的运动。
2.条件:有一定的水平初速度;只受重力的作用(忽略空气阻力)
3.特点:①
有水平初速度
②
只受重力作用
③
a=g
④
匀变速曲线运动
二、运动规律:
水平方向:
匀速直线运动.
在竖直方向:自由落体运动.
三、公式:
1.加速度
2.速度
3.位移
求解常见思路:化曲线运动为直线运动
平抛运动基本规律
①
加速度:
水平方向:合外力为0,a=0
竖直方向:合外力为G,a=g
合运动:a=g、方向竖直向下
②速度:
合速度
方向
:tanθ=
③位移:
x=vot
y=
合位移:s=
方向:
tanα=
tanθ
=2tanα
a、运动时间和射程:水平方向和竖直方向的两个分运动既具有独立性,又具有等时性.
所以运动时间为
即运动时间由高度h惟一决定
b、水平射程为
即由v0、h共同决定
c、合速度
④结论总结
d、速度的变化量
g=△v/△t,
△t时间内速度改变量相等,
即△v=g△t,
△v方向是竖直向下的.
例1、一水平匀速飞行的飞机上丢下一炸弹,问在地面上的人看来,它们作什么运动?在飞行员看来,这颗炸弹作什么运动?
答:(1)地面上的人看到炸弹作平抛运动。因炸弹离开飞机时由于惯性具有与飞机飞行速度相同的水平初速度,且炸弹只在重力作用下运动,所以是平抛运动。
(2)飞行员看到炸弹作自由落体运动。因炸弹与飞机具有相同的水平速度,相对初速度为零,炸弹在重力作用下远离飞机,所以是自由落体运动。
例2、如图,树枝上的一只松鼠看到一个猎人正用枪对准它,为了逃脱即将来临的厄运,它想让自己落到地面上逃走。但是就在它掉离树枝的瞬间子弹恰好射出枪口,问松鼠能逃脱厄运吗?
答:不能。因子弹和松鼠在竖直方向都是自由落体运动,竖直方向的位移总是相同的,所以只要在子弹的射程内,就一定能射中松鼠,松鼠在劫难逃。
我闪!!!
哪里逃?
这样也能打中!
例3、在水平路上行驶的汽车,遇到一个壕沟,汽车的速度至少为多大,才能越过这个壕沟?
(g=10m/s2)
25米
5米
【答案】
例4、如图所示,在倾角为370的斜面底端的正上方H处,平抛一小球,该小球垂直打在斜面上的一点,试求小球抛出时的初速度和飞行时间。
H
v0
370
解:画出示意图
由平抛运动规律X=Vo
t
Y=(1/2)gt?
由几何关系得:
(H-
Y)/
X=tan
370
H
v0
370
Vx
Vy
tan530=
分解位移:根据位移中分运动和合运动的大小和方向(角度)关系进行求解
例5、如图所示,A、B两球间用长6m的细线相连,两球相隔0.8s先后从同一高度处以4.5m/s的初速度平抛,则A球抛出几秒后A、B
间的细线被拉直?在这段时间内A球的位移是多大?不计空气阻力,g=10m/s2。
B
A
B
′
A′
B
A
B
′
A′
解:由平抛运动规律可得
:
xA=v0
t
yA=1/2×g
t
2
xB
=v0
(t-0.8)
yB=1/2×g(t-0.8)
2
l
2
=(xA-xB)
2
+(yA-yB)
2
代入数字得
36
=(4.5×0.8)
2
+1/2×10×
(1.6t-0.64)
解得
t=1s
xA=v0
t=4.5m
yA=1/2×g
t
2=5m
sA
2
=xA
2
+yA
2=4.5
2
+5
2
=45.25
sA
=6.73m
例6、已知排球场半场长L,网高H,如图示,若队员在离网水平
距离d
处竖直跳起水平扣球时,不论以多大的速度击球,都不能把球击在对方场地内,则队员应在离地多高处击球?
h
H
d
v
L
h
H
d
v
L
解:设高度为h,当运动员用速度v1扣球时,球刚好压边线,
用速度v2扣球时,球刚好触网,
若v1
=
v2
=
v,则既触网又压边线
不能把球击在对方场地内,则
斜抛运动
1.
轨迹:(如图)
2.
水平速度:
水平位移:
3.
竖直速度:
竖直位移:
x=v0tcos?
vx=v0cos?
vy=v0sin?
-
gt
Hm
x
y
O
v0
特点:物体所受的合力为恒力,且与初速度的方向垂直(初速度的方向不一定是水平方向,合力的方向也不一定是竖直方向,加速度大小不一定等于重力加速度。)
处理方法:可看成某一方向的匀速直线运动和垂直此方向的匀加速直线运动的合运动。(处理类平抛运动的方法与处理平抛运动的方法类似,但要分清其加速度的大小和方向。)
类平抛运动
类平抛运动的求解方法
(1)常规分解法:将类平抛运动分解为沿初速度方向的匀速直线运动和垂直于初速度方向(即沿合力的方向)的匀加速直线运动,两分运动彼此独立,互不影响,且与合运动具有等时性.
(2)特殊分解法:对于有些问题,可以过抛出点建立适当的直角坐标系,将加速度分解为ax、ay,初速度v0分解为vx、vy,然后分别在x、y方向列方程求解.
例1、如图4-2-8所示,有一倾角为30°的光滑斜面,斜面长L为10
m,一小球从斜面顶端以10
m/s的速度在斜面上沿水平方向抛出.求:(g取10
m/s2)
(1)小球沿斜面滑到底端时的水平位移x.
(2)小球到达斜面底端时的速度大小.
答案:(1)20
m (2)14.1
m/s
例2、质量为m的飞机以水平速度v0,飞离跑道后逐渐上升,若飞机在此过程中水平速度保持不变,同时受到重力和竖直向上的恒定升力(该升力由其他力的合力提供,不含重力).今测得当飞机在水平方向的位移为l时,它的上升高度为h,如图所示,
求:(1)飞机受到的升力大小?
[思路点拨] 本题以曲线运动为背景,考查运动的合成与分解问题,解答的方法是将飞机的运动分解成水平和竖直两个方向上的直线运动.
归纳拓展:
(1)类平抛运动规律与平抛运动规律相同,处理方法也相同.平抛运动的两个重要推论也适用于类平抛运动.
(2)解答类平抛运动问题时,不一定按水平方向和竖直方向进行分解,可以按初速度方向和合外力方向来分解.
