小升初数学衔接课程(精华版)-课题3 展开与折叠 通用版
文档属性
| 名称 | 小升初数学衔接课程(精华版)-课题3 展开与折叠 通用版 |
|
|
| 格式 | doc | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-09-28 00:00:00 | ||
图片预览


文档简介
课题3
展开与折叠
一、【学习目标】
1.能进行图形的分割组合;
2.会判断正方体的相对面;
3.能区分几何体的表面展开图,会判断最短路线.
二、【知识梳理】
1.
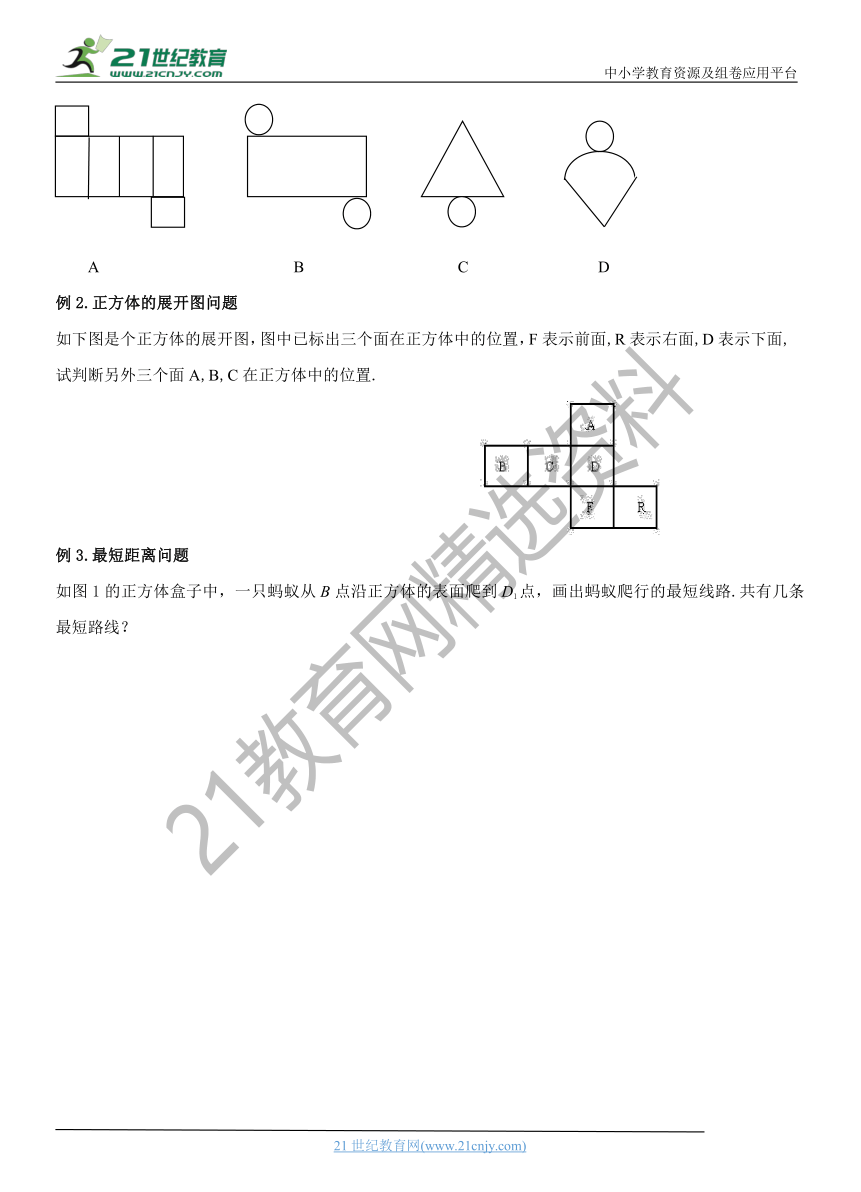
圆柱、圆锥、正三棱锥、正四棱锥、正五棱锥、正三棱柱的展开图:
2.
正方体的平面展开图:
(1)设法将一个正方体展开,需要剪开几条棱?几条棱没剪开?
(2)你能将正方体展开成下列形式吗?
(3)正方体的展开图有哪些?(用边长为1厘米的正方形画)
①最多4个面连在一起的情况
②最多3个面连在一起的情况
③最多2个面连在一起的情况
3.总结:正方体的展开图如下:
三、【典例精析】
例1.常见几何体的展开图问题
(1)下列展开图中,不能围成几何体的是(
).
(2)下列各个平面图形中,属于圆锥的表面展开图的是(
)
A
B
C
D
例2.正方体的展开图问题
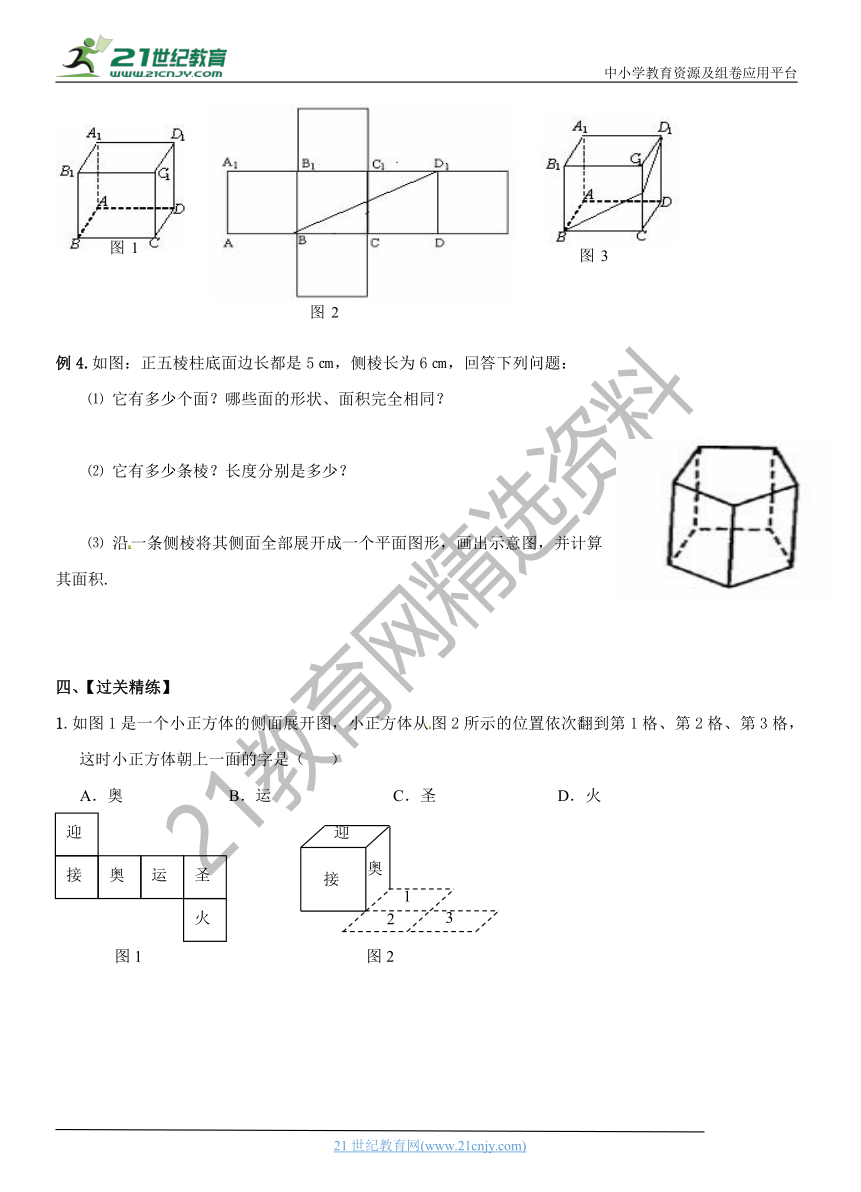
如下图是个正方体的展开图,图中已标出三个面在正方体中的位置,F表示前面,R表示右面,D表示下面,
试判断另外三个面A,B,C在正方体中的位置.
例3.最短距离问题
如图1的正方体盒子中,一只蚂蚁从B点沿正方体的表面爬到D1点,画出蚂蚁爬行的最短线路.共有几条最短路线?
例4.如图:正五棱柱底面边长都是5㎝,侧棱长为6㎝,回答下列问题:
⑴
它有多少个面?哪些面的形状、面积完全相同?
⑵
它有多少条棱?长度分别是多少?
⑶
沿一条侧棱将其侧面全部展开成一个平面图形,画出示意图,并计算其面积.
四、【过关精练】
1.如图1是一个小正方体的侧面展开图,小正方体从图2所示的位置依次翻到第1格、第2格、第3格,这时小正方体朝上一面的字是(
)
A.奥
B.运
C.圣
D.火
迎
接
奥
运
圣
火
图1
迎
接
奥
1
2
3
图2
2.如图,下列图形经过折叠不能围成棱柱的是(
)
A
B
C
D
3.如下左图是一个正四面体,它的四个面都是正三角形,现沿它的三条棱AC、BC、CD剪开展成平面图形,则所得的展开图是(
)
[]
4..如下图,哪个是正方体的展开图(
5.如图所示的立方体,如果把它展开,可以是下列图形中的(
)
[]
[]
6.将图(1)中的图形折叠起来围成一个正方体,应该得到图(2)中的(
)[]
7.从棱柱的折叠过程可以知道:
(1)棱柱的表面展开图是两个______的多边形作底面,几个_______作侧面;
(2)
棱柱的底面边数与侧面数_______;
(3)
棱柱的两个底面要分别在侧面展开图的_______.
8.部分几何体的平面展开图:
(1)圆柱的表面展开图是_________作底面;和______________作侧面.[]
(2)圆锥的表面展开图是___________作底面;和_______________作侧面
9.下图所示的平面图形是由哪几种几何体的表面展开的?
10.在4×4的方格中,取适当的相连的5个小正方形可折叠成无盖的正方体盒子,请你在图由中画岀这样的相连的5个正方形,在图中最多能剪折多少个?
11.小华用如下图所示的胶滚沿从左到右的方向将图案滚涂到墙上,则符合胶滚涂出的
一个正确图案是(
)
13.如下图是一食品包装盒侧面展开图.
(1)指出这个包装盒的多面体形状的名称;
(2)计算出这个多面体的侧面积(单位:)
14.如下图是一张铁皮.
(1)计算铁皮的面积;
(2)它能否做成一个长方体的盒子?若能,求出它的体积;
若不能,请说明理由.
[]
[]
展开与折叠
一、【学习目标】
1.能进行图形的分割组合;
2.会判断正方体的相对面;
3.能区分几何体的表面展开图,会判断最短路线.
二、【知识梳理】
1.
圆柱、圆锥、正三棱锥、正四棱锥、正五棱锥、正三棱柱的展开图:
2.
正方体的平面展开图:
(1)设法将一个正方体展开,需要剪开几条棱?几条棱没剪开?
(2)你能将正方体展开成下列形式吗?
(3)正方体的展开图有哪些?(用边长为1厘米的正方形画)
①最多4个面连在一起的情况
②最多3个面连在一起的情况
③最多2个面连在一起的情况
3.总结:正方体的展开图如下:
三、【典例精析】
例1.常见几何体的展开图问题
(1)下列展开图中,不能围成几何体的是(
).
(2)下列各个平面图形中,属于圆锥的表面展开图的是(
)
A
B
C
D
例2.正方体的展开图问题
如下图是个正方体的展开图,图中已标出三个面在正方体中的位置,F表示前面,R表示右面,D表示下面,
试判断另外三个面A,B,C在正方体中的位置.
例3.最短距离问题
如图1的正方体盒子中,一只蚂蚁从B点沿正方体的表面爬到D1点,画出蚂蚁爬行的最短线路.共有几条最短路线?
例4.如图:正五棱柱底面边长都是5㎝,侧棱长为6㎝,回答下列问题:
⑴
它有多少个面?哪些面的形状、面积完全相同?
⑵
它有多少条棱?长度分别是多少?
⑶
沿一条侧棱将其侧面全部展开成一个平面图形,画出示意图,并计算其面积.
四、【过关精练】
1.如图1是一个小正方体的侧面展开图,小正方体从图2所示的位置依次翻到第1格、第2格、第3格,这时小正方体朝上一面的字是(
)
A.奥
B.运
C.圣
D.火
迎
接
奥
运
圣
火
图1
迎
接
奥
1
2
3
图2
2.如图,下列图形经过折叠不能围成棱柱的是(
)
A
B
C
D
3.如下左图是一个正四面体,它的四个面都是正三角形,现沿它的三条棱AC、BC、CD剪开展成平面图形,则所得的展开图是(
)
[]
4..如下图,哪个是正方体的展开图(
5.如图所示的立方体,如果把它展开,可以是下列图形中的(
)
[]
[]
6.将图(1)中的图形折叠起来围成一个正方体,应该得到图(2)中的(
)[]
7.从棱柱的折叠过程可以知道:
(1)棱柱的表面展开图是两个______的多边形作底面,几个_______作侧面;
(2)
棱柱的底面边数与侧面数_______;
(3)
棱柱的两个底面要分别在侧面展开图的_______.
8.部分几何体的平面展开图:
(1)圆柱的表面展开图是_________作底面;和______________作侧面.[]
(2)圆锥的表面展开图是___________作底面;和_______________作侧面
9.下图所示的平面图形是由哪几种几何体的表面展开的?
10.在4×4的方格中,取适当的相连的5个小正方形可折叠成无盖的正方体盒子,请你在图由中画岀这样的相连的5个正方形,在图中最多能剪折多少个?
11.小华用如下图所示的胶滚沿从左到右的方向将图案滚涂到墙上,则符合胶滚涂出的
一个正确图案是(
)
13.如下图是一食品包装盒侧面展开图.
(1)指出这个包装盒的多面体形状的名称;
(2)计算出这个多面体的侧面积(单位:)
14.如下图是一张铁皮.
(1)计算铁皮的面积;
(2)它能否做成一个长方体的盒子?若能,求出它的体积;
若不能,请说明理由.
[]
[]
同课章节目录
