勾股定理教学案
图片预览

文档简介
尚堂中学课时教·学案
授课时间:
年级 八年级 学科 数学 主备人 王文勇
课题 勾股定理 课 型 新授
学习目标 1、了解勾股定理的由来,经历探索勾股定理的过程.2、能运用勾股定理解决简单的实际问题
重难点 勾股定理的证明
学 习 过 程 感悟及修订
探索新知 1、甲乙两图是由边长相等的小正方形组成的图形,通过观察、计算你能否发现图中三个正方形面积之间的关系? (甲) (乙)2、由三个正方形面积之间的关系,请探索三个正方形所围成的直角三角形三条边之间的数量关系? 二、归纳总结 1、 如果直角三角形的两直角边长分别为 a、b,斜边为c,那么 2、如下图,为由四个完全相同的直角三角形拼成的图形,请你利用该图形来验证1中的结论
学 习 过 程 感悟及修订
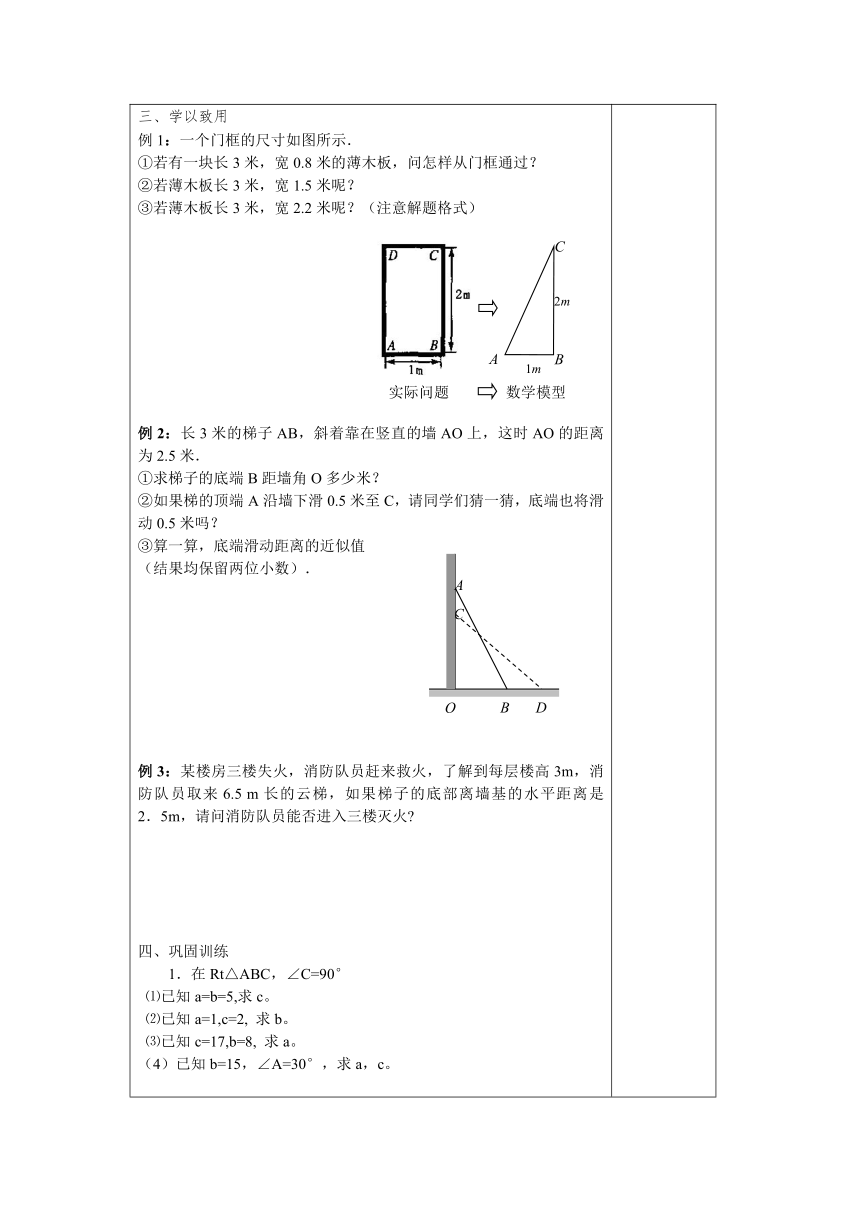
学以致用例1:一个门框的尺寸如图所示.①若有一块长3米,宽0.8米的薄木板,问怎样从门框通过?②若薄木板长3米,宽1.5米呢?③若薄木板长3米,宽2.2米呢?(注意解题格式) 例2:长3米的梯子AB,斜着靠在竖直的墙AO上,这时AO的距离为2.5米.①求梯子的底端B距墙角O多少米?②如果梯的顶端A沿墙下滑0.5米至C,请同学们猜一猜,底端也将滑动0.5米吗?③算一算,底端滑动距离的近似值(结果均保留两位小数).例3:某楼房三楼失火,消防队员赶来救火,了解到每层楼高3m,消防队员取来6.5 m长的云梯,如果梯子的底部离墙基的水平距离是2.5m,请问消防队员能否进入三楼灭火 四、巩固训练1.在Rt△ABC,∠C=90°⑴已知a=b=5,求c。⑵已知a=1,c=2, 求b。⑶已知c=17,b=8, 求a。(4)已知b=15,∠A=30°,求a,c。2.已知直角三角形的两边长分别为5和12,求第三边。3.已知等腰三角形腰长是10,底边长是16,求这个等腰三角形的面积。4.已知:如图,四边形ABCD中,AD∥BC,AD⊥DC, AB⊥AC,∠B=60°,CD=1cm,求BC的长。
学 习 过 程 感悟及修订
达标检测 1、求出下列直角三角形中未知的边.2、一个高1.5米、宽0.8米的长方形门框,需要在其相对的顶点间用一条木条加固,则需木条长为 。3、从电杆离地面5m处向地面拉一条长为7m的钢缆,则地面钢缆A到电线杆底部B的距离为 。4、有一个边长为50dm的正方形洞口,想用一个圆盖盖住这个洞口,圆的直径至少为 (结果保留整数)5、一旗杆离地面6m处折断,其顶部落在离旗杆底部8m处,则旗杆折断前高 6、如图,滑杆在机械槽内运动,∠ACB为直角,已知滑杆AB长100cm,顶端A在AC上运动,量得滑杆下端B距C点的距离为60cm,当端点B向右移动20cm时,滑杆顶端A下滑多长? 7、长方形零件尺寸如图(单位:mm), 求两孔中心的距离。(精确到0.1mm)
尚堂中学教务处
A
B
C
A
B
C
B
C
1m
2m
A
实际问题
数学模型
O
B
D
CC
A
10
45°
6
10
10
30°
15
8
B
A
C
A
E
B
D
C
21
40
21
60
A
B
C
授课时间:
年级 八年级 学科 数学 主备人 王文勇
课题 勾股定理 课 型 新授
学习目标 1、了解勾股定理的由来,经历探索勾股定理的过程.2、能运用勾股定理解决简单的实际问题
重难点 勾股定理的证明
学 习 过 程 感悟及修订
探索新知 1、甲乙两图是由边长相等的小正方形组成的图形,通过观察、计算你能否发现图中三个正方形面积之间的关系? (甲) (乙)2、由三个正方形面积之间的关系,请探索三个正方形所围成的直角三角形三条边之间的数量关系? 二、归纳总结 1、 如果直角三角形的两直角边长分别为 a、b,斜边为c,那么 2、如下图,为由四个完全相同的直角三角形拼成的图形,请你利用该图形来验证1中的结论
学 习 过 程 感悟及修订
学以致用例1:一个门框的尺寸如图所示.①若有一块长3米,宽0.8米的薄木板,问怎样从门框通过?②若薄木板长3米,宽1.5米呢?③若薄木板长3米,宽2.2米呢?(注意解题格式) 例2:长3米的梯子AB,斜着靠在竖直的墙AO上,这时AO的距离为2.5米.①求梯子的底端B距墙角O多少米?②如果梯的顶端A沿墙下滑0.5米至C,请同学们猜一猜,底端也将滑动0.5米吗?③算一算,底端滑动距离的近似值(结果均保留两位小数).例3:某楼房三楼失火,消防队员赶来救火,了解到每层楼高3m,消防队员取来6.5 m长的云梯,如果梯子的底部离墙基的水平距离是2.5m,请问消防队员能否进入三楼灭火 四、巩固训练1.在Rt△ABC,∠C=90°⑴已知a=b=5,求c。⑵已知a=1,c=2, 求b。⑶已知c=17,b=8, 求a。(4)已知b=15,∠A=30°,求a,c。2.已知直角三角形的两边长分别为5和12,求第三边。3.已知等腰三角形腰长是10,底边长是16,求这个等腰三角形的面积。4.已知:如图,四边形ABCD中,AD∥BC,AD⊥DC, AB⊥AC,∠B=60°,CD=1cm,求BC的长。
学 习 过 程 感悟及修订
达标检测 1、求出下列直角三角形中未知的边.2、一个高1.5米、宽0.8米的长方形门框,需要在其相对的顶点间用一条木条加固,则需木条长为 。3、从电杆离地面5m处向地面拉一条长为7m的钢缆,则地面钢缆A到电线杆底部B的距离为 。4、有一个边长为50dm的正方形洞口,想用一个圆盖盖住这个洞口,圆的直径至少为 (结果保留整数)5、一旗杆离地面6m处折断,其顶部落在离旗杆底部8m处,则旗杆折断前高 6、如图,滑杆在机械槽内运动,∠ACB为直角,已知滑杆AB长100cm,顶端A在AC上运动,量得滑杆下端B距C点的距离为60cm,当端点B向右移动20cm时,滑杆顶端A下滑多长? 7、长方形零件尺寸如图(单位:mm), 求两孔中心的距离。(精确到0.1mm)
尚堂中学教务处
A
B
C
A
B
C
B
C
1m
2m
A
实际问题
数学模型
O
B
D
CC
A
10
45°
6
10
10
30°
15
8
B
A
C
A
E
B
D
C
21
40
21
60
A
B
C
