菱形的性质
图片预览
文档简介
尚堂中学课时教·学案
授课时间:
年级 八 年 级 学科 数学 主备人 王文勇
课题 菱形的性质 课 型 新 授
学习目标 1.掌握菱形的性质,学会运用菱形的性质解决一些问题2.经历探索菱形性质的过程
重难点 菱形的性质.
学 习 过 程 感悟及修订
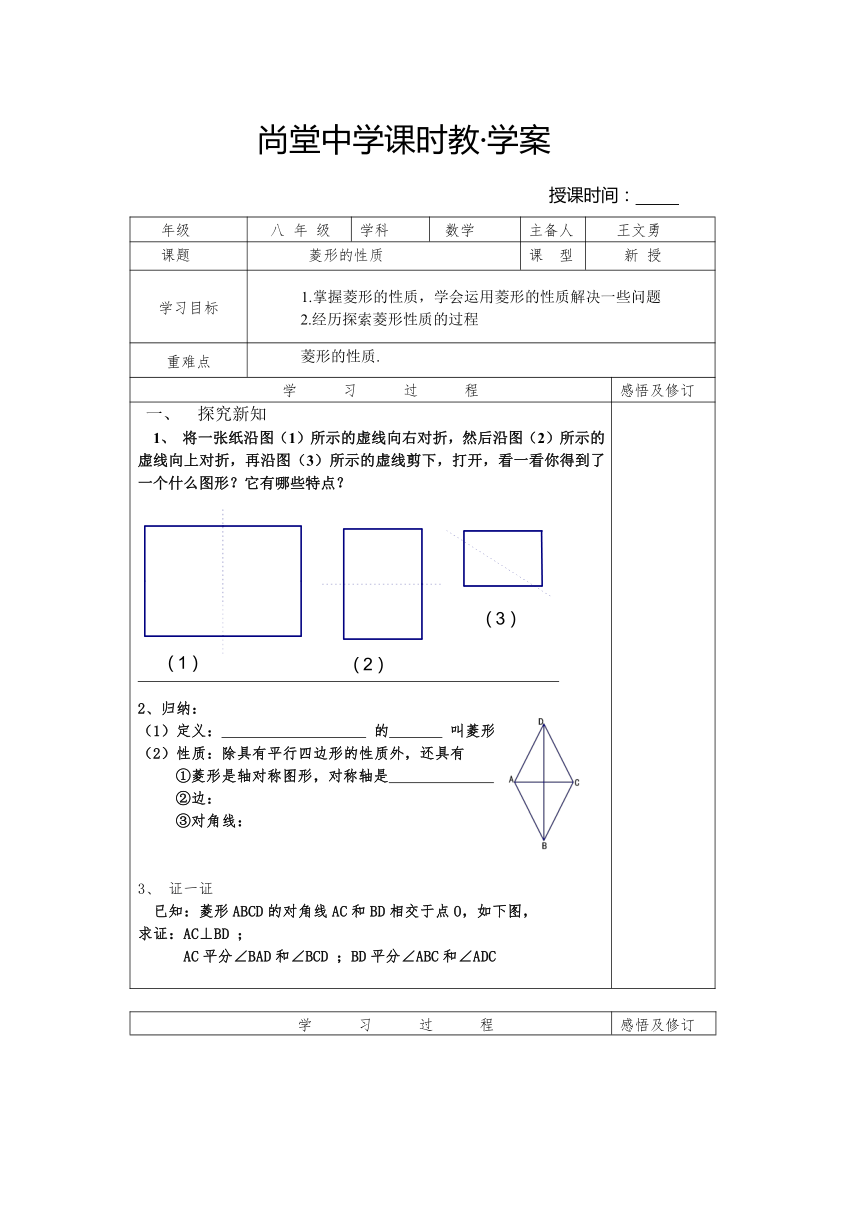
探究新知 1、 将一张纸沿图(1)所示的虚线向右对折,然后沿图(2)所示的虚线向上对折,再沿图(3)所示的虚线剪下,打开,看一看你得到了一个什么图形?它有哪些特点?2、归纳:(1)定义: 的 叫菱形(2)性质:除具有平行四边形的性质外,还具有①菱形是轴对称图形,对称轴是 ②边: ③对角线:3、 证一证 已知:菱形ABCD的对角线AC和BD相交于点O,如下图,求证:AC⊥BD ; AC平分∠BAD和∠BCD ;BD平分∠ABC和∠ADC
学 习 过 程 感悟及修订
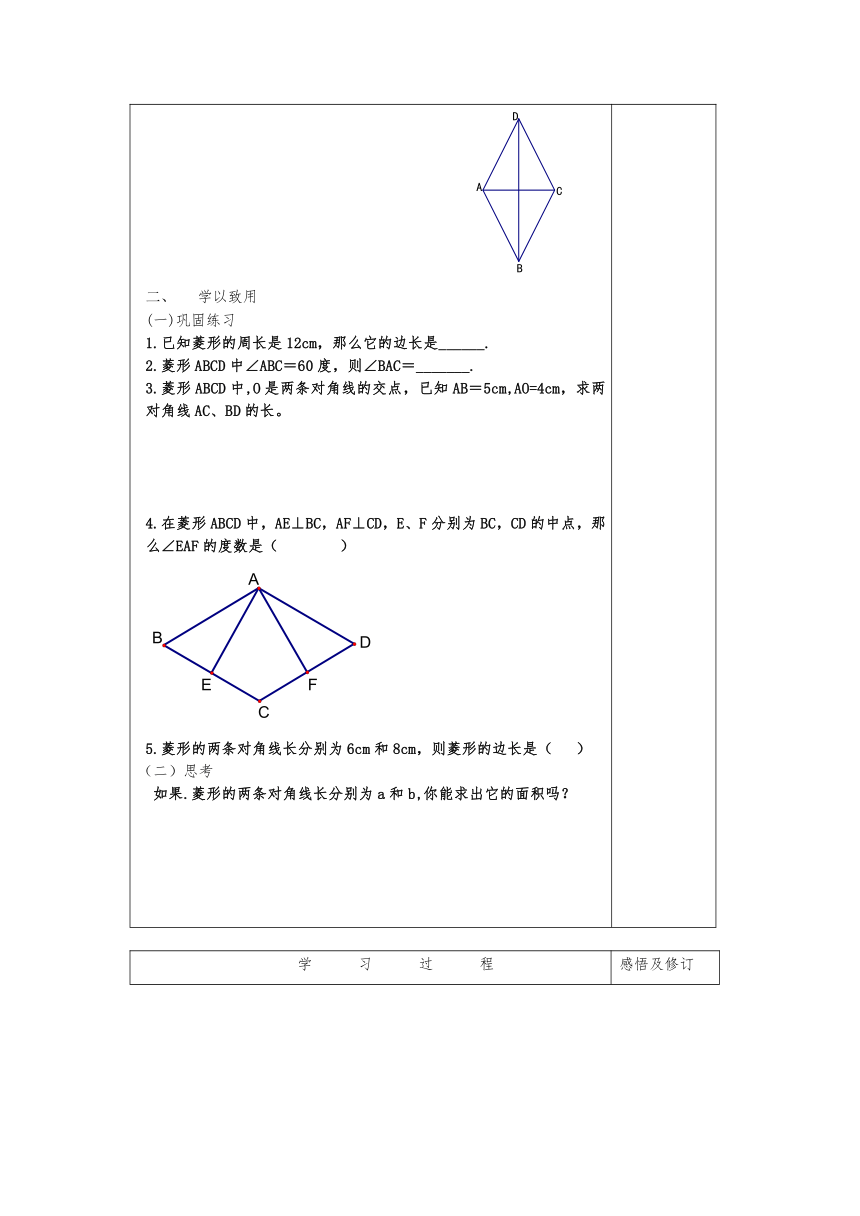
学以致用(一)巩固练习1.已知菱形的周长是12cm,那么它的边长是______.2.菱形ABCD中∠ABC=60度,则∠BAC=_______.3.菱形ABCD中,O是两条对角线的交点,已知AB=5cm,AO=4cm,求两对角线AC、BD的长。4.在菱形ABCD中,AE⊥BC,AF⊥CD,E、F分别为BC,CD的中点,那么∠EAF的度数是( )5.菱形的两条对角线长分别为6cm和8cm,则菱形的边长是( )(二)思考 如果.菱形的两条对角线长分别为a和b,你能求出它的面积吗?
学 习 过 程 感悟及修订
归纳:菱形的面积=底×高=练习:1. 菱形的一个内角为120°,平分这个内角的对角线长为11厘米,菱形的周长为______.2. 菱形的对角线的一半的长分别为8 cm和11 cm,则菱形的面积是_______.3. 菱形的面积为64平方厘米,两条对角线的比为1∶2 ,那么菱形的边长为_______.4.已知,菱形对角线长分别为12cm和16cm,求菱形的高。5、如图,菱形花坛ABCD的周长为80m, ∠ABC=60度,沿着菱形的对角线修建了两条小路AC和BD,求两条小路的长和花坛的面积(分别精确到0.01m和0.01m )小结 矩形菱形定义性质四、达标检测1.菱形的两条对角线长分别为16cm,12cm,那么这个菱形的高是_______.
学 习 过 程 感悟及修订
2.已知菱形两邻角的比是1:2,周长是40cm,则较短对角线长是________.3.菱形的面积为50cm2,一个内角为30°,则其边长为______.4.菱形一边与两条对角线所构成两角之比为2:7,则它的各角为______. 5.菱形ABCD,若∠A:∠B=2:1,∠CAD的平分线AE和边CD之间的关系是( ). A.相等 B.互相垂直且不平分C.互相平分且不垂直 D.垂直且平分6.在菱形ABCD中,AE⊥BC于E,菱形ABCD面积等于24cm2,AE=6cm,则AB长为( ). A.12cm B.8cm C.4cm D.2cm7.如图,在菱形ABCD中,E是AB的中点,作EF∥BC,交AC于点F,如果EF=4,那么CD的长为( ).A.2 B.4 C.6 D.88、已知如图,菱形ABCD中,E是AB的中点,且DE⊥AB,AE=2。求(1)∠ABC的度数; (2)对角线AC、BD的长; (3)菱形ABCD的面积。
尚堂中学教务处
A
B
C
D
E
O
授课时间:
年级 八 年 级 学科 数学 主备人 王文勇
课题 菱形的性质 课 型 新 授
学习目标 1.掌握菱形的性质,学会运用菱形的性质解决一些问题2.经历探索菱形性质的过程
重难点 菱形的性质.
学 习 过 程 感悟及修订
探究新知 1、 将一张纸沿图(1)所示的虚线向右对折,然后沿图(2)所示的虚线向上对折,再沿图(3)所示的虚线剪下,打开,看一看你得到了一个什么图形?它有哪些特点?2、归纳:(1)定义: 的 叫菱形(2)性质:除具有平行四边形的性质外,还具有①菱形是轴对称图形,对称轴是 ②边: ③对角线:3、 证一证 已知:菱形ABCD的对角线AC和BD相交于点O,如下图,求证:AC⊥BD ; AC平分∠BAD和∠BCD ;BD平分∠ABC和∠ADC
学 习 过 程 感悟及修订
学以致用(一)巩固练习1.已知菱形的周长是12cm,那么它的边长是______.2.菱形ABCD中∠ABC=60度,则∠BAC=_______.3.菱形ABCD中,O是两条对角线的交点,已知AB=5cm,AO=4cm,求两对角线AC、BD的长。4.在菱形ABCD中,AE⊥BC,AF⊥CD,E、F分别为BC,CD的中点,那么∠EAF的度数是( )5.菱形的两条对角线长分别为6cm和8cm,则菱形的边长是( )(二)思考 如果.菱形的两条对角线长分别为a和b,你能求出它的面积吗?
学 习 过 程 感悟及修订
归纳:菱形的面积=底×高=练习:1. 菱形的一个内角为120°,平分这个内角的对角线长为11厘米,菱形的周长为______.2. 菱形的对角线的一半的长分别为8 cm和11 cm,则菱形的面积是_______.3. 菱形的面积为64平方厘米,两条对角线的比为1∶2 ,那么菱形的边长为_______.4.已知,菱形对角线长分别为12cm和16cm,求菱形的高。5、如图,菱形花坛ABCD的周长为80m, ∠ABC=60度,沿着菱形的对角线修建了两条小路AC和BD,求两条小路的长和花坛的面积(分别精确到0.01m和0.01m )小结 矩形菱形定义性质四、达标检测1.菱形的两条对角线长分别为16cm,12cm,那么这个菱形的高是_______.
学 习 过 程 感悟及修订
2.已知菱形两邻角的比是1:2,周长是40cm,则较短对角线长是________.3.菱形的面积为50cm2,一个内角为30°,则其边长为______.4.菱形一边与两条对角线所构成两角之比为2:7,则它的各角为______. 5.菱形ABCD,若∠A:∠B=2:1,∠CAD的平分线AE和边CD之间的关系是( ). A.相等 B.互相垂直且不平分C.互相平分且不垂直 D.垂直且平分6.在菱形ABCD中,AE⊥BC于E,菱形ABCD面积等于24cm2,AE=6cm,则AB长为( ). A.12cm B.8cm C.4cm D.2cm7.如图,在菱形ABCD中,E是AB的中点,作EF∥BC,交AC于点F,如果EF=4,那么CD的长为( ).A.2 B.4 C.6 D.88、已知如图,菱形ABCD中,E是AB的中点,且DE⊥AB,AE=2。求(1)∠ABC的度数; (2)对角线AC、BD的长; (3)菱形ABCD的面积。
尚堂中学教务处
A
B
C
D
E
O
