六年级上册数学试题 第五单元 圆 第四节 扇形 同步测试 人教版 含答案
文档属性
| 名称 | 六年级上册数学试题 第五单元 圆 第四节 扇形 同步测试 人教版 含答案 |  | |
| 格式 | docx | ||
| 文件大小 | 171.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-23 12:13:20 | ||
图片预览


文档简介
六年级上册数学试题
第五单元 圆
第四节 扇形 同步测试
一、填空题(共5题;共21分)
1.一条弧和经过这条弧两端的两条半径围成的图形叫作________,在这种图形中,顶点在圆心的角叫作________。
2.圆心角为90°,半径为6米的扇形,它的面积是________平方米.
3.如图,为了绿化环境,在小区长方形空地的四角画出四个半径为2的扇形空地进行绿化,则绿化的总面积为________.(结果保留π)
4.在同一个圆中,扇形的大小与这个扇形的________有关。
5.扇形是________图形,它有________条对称轴。
二、判断题(共4题;共12分)
6.同一圆内圆心角的大小决定扇形的大小.
7.圆心角大的扇形一定比圆心角小的扇形大。
8.圆心角60°的扇形一定比圆心角40°的扇形面积大.
9.扇形是圆的一部分,所以扇形的面积小于圆的面积。
三、选择题(共7题;共35分)
10.一半圆的周长为10.28m,则半圆的面积为( )m2
A.?3.14?????????????????????????????????????B.?6.28?????????????????????????????????????C.?4.07?????????????????????????????????????D.?1.57
11.以下哪个选项是扇形的定义(?? )
A.??一条弧和经过这条弧两端的两条半径所围成的图形??????????
B.??圆上两点与圆内一点连线及其弧围成的部分
C.??圆外两点与圆心连线围成的部分????????????????????????
D.?? 一条弧和经过这条弧两端的任意两条线段所围成的图形
12.下面(??? )的阴影部分是扇形。
A.????????????????????????????????B.????????????????????????????????C.?
13.已知扇形的圆心角为120°,半径为6,则扇形的弧长是(? ). ?????
A.?3 ???????????????????????????????????????B.?4 ???????????????????????????????????????C.?5 ???????????????????????????????????????D.?6
14.以下哪个选项是圆心角的定义(?? )
A.??顶点在圆外的角????????????B.??顶点在圆内的角????????????C.??顶点在圆心的角????????????D.?? 顶点在圆上的角
15.把一张直径为4厘米的圆形纸片对折两次得到一个扇形,这个扇形的周长是( ??)厘米。
A.?π???????????????????????????????????????B.?4+π???????????????????????????????????????C.?4π???????????????????????????????????????D.?π
16.下图扇形的半径是r。请你想象,用这个扇形围成一个高为h的圆锥(接缝处不计)。圆锥的高h与扇形半径r之间的关系是( ??)。
A.?h>r???????????????????????????????????B.?h四、解答题(共4题;共20分)
17.如图,该平行四边形面积是40平方厘米,底是10厘米,求阴影部分面积。(单位:厘米)
18.一块正方形的草地,边长为4m,两个对角各有一棵树,树上各栓了一只羊。栓羊的绳子长都是4m。两只羊都能吃到青草的面积是多少平方米?
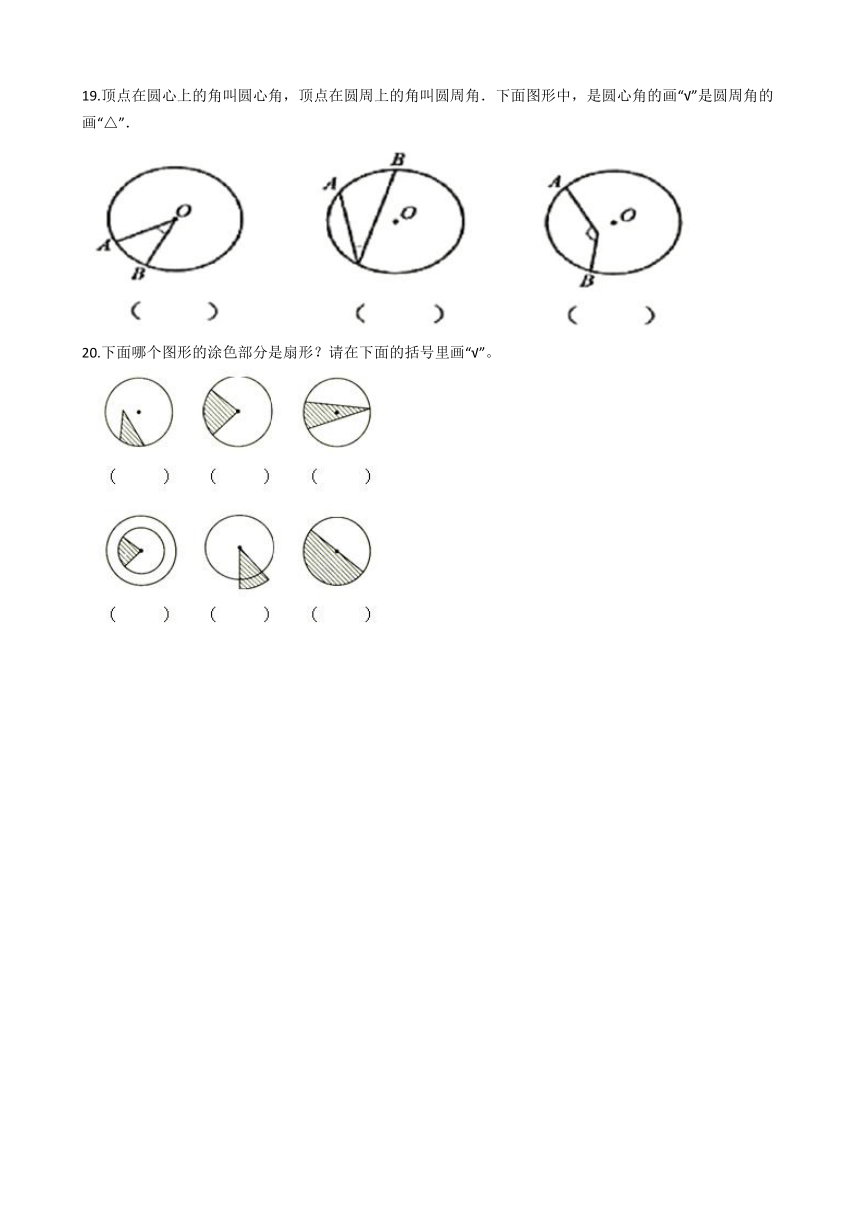
19.顶点在圆心上的角叫圆心角,顶点在圆周上的角叫圆周角.下面图形中,是圆心角的画“√”是圆周角的画“△”.
20.下面哪个图形的涂色部分是扇形?请在下面的括号里画“√”。
答案解析部分
一、填空题
1.【答案】 扇形;圆心角
【解析】【解答】 一条弧和经过这条弧两端的两条半径围成的图形叫作扇形, 在这种图形中,顶点在圆心的角叫作圆心角。
故答案为:扇形;圆心角。
【分析】根据扇形和圆心角的定义填写。
2.【答案】 28.26
【解析】【解答】解:3.14×62×
=3.14×36×
=3.14×9
=28.26(平方米)
故答案为:28.26。
【分析】扇形圆心角占360°的几分之几,扇形面积就占所在圆面积的几分之几,根据公式计算扇形面积即可。
3.【答案】4π
【解析】【解答】解:π×2?=4π
故答案为:4π
【分析】四个扇形半径相等,每个扇形的圆心角都是90°,那么四个扇形刚好组成一个半径是2的圆,根据圆面积公式计算总面积即可.
4.【答案】圆心角
【解析】【解答】在同一个圆中,扇形的大小与这个扇形的圆心角有关.
故答案为:圆心角.
【分析】在同一个圆中,扇形的大小与这个扇形的圆心角大小有关,圆心角越大,扇形越大,圆心角越小,扇形越小,据此解答.
5.【答案】 轴对称;一
【解析】【解答】解:扇形是轴对称图形,它有一条对称轴。
故答案为:轴对称;一。
【分析】扇形是轴对称图形,扇形只有一条对称轴,扇形的对称轴是圆心角的平分线所在的直线。
二、判断题
6.【答案】正确
【解析】【解答】解:根据分析可得:同一圆内圆心角的大小决定了扇形的大小,说法是正确的.故答案为:正确
【分析】同一个圆的半径是相等的,扇形的半径也相等,那么扇形面积就是由圆心角的大小决定的.
7.【答案】错误
【解析】【解答】缺少条件,在同一个圆内或等圆内,原题说法错误.
故答案为:错误.
【分析】在同一个圆内或等圆内,扇形的大小与圆心角的大小有关,圆心角大的扇形一定比圆心角小的扇形大,据此解答.
8.【答案】错误
【解析】【解答】解:计算扇形面积需要知道圆心角和半径,
不知道半径的大小,就无法计算面积,也就更不能比较面积大小了;
故答案为:错误.
【分析】计算扇形面积需要知道半径的大小和圆心角,只知道圆心角而不知道半径,则无法计算扇形的面积,也无法比较大小.
9.【答案】错误
【解析】【解答】解:扇形是圆的一部分,如果扇形的半径和圆的半径相等,那么扇形面积就小于圆的面积。原题说法错误。
故答案为:错误
【分析】扇形的面积比所在圆的面积小,原题没有说明半径的长短,所以无法确定面积的大小。
三、选择题
10.【答案】 B
【解析】【解答】解:设半圆的直径是d,
3.14×d÷2+d=10.28
? ? ?? 1.57d+d=10.28
??????????? 2.57d=10.28
?????????????????? d=4
半圆的面积:3.14×(4÷2)?×=3.14×2=6.28(m?)
故答案为:B
【分析】半圆的周长包括半圆弧的长度和一条直径的长度,因此设直径是d,然后根据周长列出一个方程,解方程求出直径,再根据圆面积公式计算半圆的面积即可.
11.【答案】 A
【解析】【解答】解:根据扇形的定义可知,?一条弧和经过这条弧两端的两条半径所围成的图形叫作扇形.
故答案为:A
【分析】扇形是圆的一部分,是一条弧和经过这条弧两端的两条半径所围成的图形;由此判断并选择即可.
12.【答案】C
【解析】【解答】根据分析可知,A、B图中都不是由半径和圆弧组成的,不是扇形,C图阴影部分是扇形.
故答案为:C.
【分析】根据扇形的定义:一条弧和经过这条弧两端的两条半径所围成的图形叫扇形,据此判断即可.
13.【答案】 B
【解析】【解答】解:π×6×2×
=π×12×
=4π
故答案为:B
【分析】扇形圆心角占360度的几分之几,扇形弧长就占所在圆周长的几分之几,由此计算扇形的弧长即可.
14.【答案】 C
【解析】【解答】解:根据圆心角的定义可知,顶点在圆心的角才叫圆心角.
故答案为:C
【分析】圆心角是顶点在圆心的角,圆心角的两条边是两条半径,由此判断并选择即可.
15.【答案】 B
【解析】【解答】根据分析可得,扇形的周长是:π×4×+4=π+4(厘米).
故答案为:B.
【分析】 把一张直径为4厘米的圆形纸片对折两次,得到的是一个圆心角是360°÷4=90°的扇形,这个扇形的周长是圆周长的+两条半径的长度,据此解答.
16.【答案】 B
【解析】【解答】 根据分析可知,圆锥的高h与扇形半径r之间的关系是:h<r.
故答案为:B.
【分析】根据题意,把该扇形围成圆锥后,扇形的半径即围成后圆锥的母线,圆锥的高与底面半径、圆锥母线构成直角三角形的三边,直角三角形中,斜边最长,所以扇形的高小于圆锥的母线(即扇形的半径r),据此判断即可.
四、解答题
17.【答案】 解:3.14×( )2× =12.56(平方厘米)
【解析】【分析】用平行四边形的面积除以底即可求出高,也就是圆的半径;阴影部分的面积是所在圆面积的, 根据圆面积公式计算阴影部分的面积即可。
18.【答案】 解:(3.14×42× )×2-4×4=9.12(m2)
答:两只羊都能吃到青草的面积是9.12平方米。
【解析】【分析】从图中可以看出,两只羊都能吃到青草的面积=圆的面积×2-正方形的面积,其中圆的面积=πr2 , 正方形的面积=边长×边长。
19.【答案】
【解析】【分析】根据圆心角和圆周角的定义作答即可。
20.【答案】
【解析】【分析】 弧和经过弧两端的半径所围成的图形叫做扇形。由此判断即可。
第五单元 圆
第四节 扇形 同步测试
一、填空题(共5题;共21分)
1.一条弧和经过这条弧两端的两条半径围成的图形叫作________,在这种图形中,顶点在圆心的角叫作________。
2.圆心角为90°,半径为6米的扇形,它的面积是________平方米.
3.如图,为了绿化环境,在小区长方形空地的四角画出四个半径为2的扇形空地进行绿化,则绿化的总面积为________.(结果保留π)
4.在同一个圆中,扇形的大小与这个扇形的________有关。
5.扇形是________图形,它有________条对称轴。
二、判断题(共4题;共12分)
6.同一圆内圆心角的大小决定扇形的大小.
7.圆心角大的扇形一定比圆心角小的扇形大。
8.圆心角60°的扇形一定比圆心角40°的扇形面积大.
9.扇形是圆的一部分,所以扇形的面积小于圆的面积。
三、选择题(共7题;共35分)
10.一半圆的周长为10.28m,则半圆的面积为( )m2
A.?3.14?????????????????????????????????????B.?6.28?????????????????????????????????????C.?4.07?????????????????????????????????????D.?1.57
11.以下哪个选项是扇形的定义(?? )
A.??一条弧和经过这条弧两端的两条半径所围成的图形??????????
B.??圆上两点与圆内一点连线及其弧围成的部分
C.??圆外两点与圆心连线围成的部分????????????????????????
D.?? 一条弧和经过这条弧两端的任意两条线段所围成的图形
12.下面(??? )的阴影部分是扇形。
A.????????????????????????????????B.????????????????????????????????C.?
13.已知扇形的圆心角为120°,半径为6,则扇形的弧长是(? ). ?????
A.?3 ???????????????????????????????????????B.?4 ???????????????????????????????????????C.?5 ???????????????????????????????????????D.?6
14.以下哪个选项是圆心角的定义(?? )
A.??顶点在圆外的角????????????B.??顶点在圆内的角????????????C.??顶点在圆心的角????????????D.?? 顶点在圆上的角
15.把一张直径为4厘米的圆形纸片对折两次得到一个扇形,这个扇形的周长是( ??)厘米。
A.?π???????????????????????????????????????B.?4+π???????????????????????????????????????C.?4π???????????????????????????????????????D.?π
16.下图扇形的半径是r。请你想象,用这个扇形围成一个高为h的圆锥(接缝处不计)。圆锥的高h与扇形半径r之间的关系是( ??)。
A.?h>r???????????????????????????????????B.?h
17.如图,该平行四边形面积是40平方厘米,底是10厘米,求阴影部分面积。(单位:厘米)
18.一块正方形的草地,边长为4m,两个对角各有一棵树,树上各栓了一只羊。栓羊的绳子长都是4m。两只羊都能吃到青草的面积是多少平方米?
19.顶点在圆心上的角叫圆心角,顶点在圆周上的角叫圆周角.下面图形中,是圆心角的画“√”是圆周角的画“△”.
20.下面哪个图形的涂色部分是扇形?请在下面的括号里画“√”。
答案解析部分
一、填空题
1.【答案】 扇形;圆心角
【解析】【解答】 一条弧和经过这条弧两端的两条半径围成的图形叫作扇形, 在这种图形中,顶点在圆心的角叫作圆心角。
故答案为:扇形;圆心角。
【分析】根据扇形和圆心角的定义填写。
2.【答案】 28.26
【解析】【解答】解:3.14×62×
=3.14×36×
=3.14×9
=28.26(平方米)
故答案为:28.26。
【分析】扇形圆心角占360°的几分之几,扇形面积就占所在圆面积的几分之几,根据公式计算扇形面积即可。
3.【答案】4π
【解析】【解答】解:π×2?=4π
故答案为:4π
【分析】四个扇形半径相等,每个扇形的圆心角都是90°,那么四个扇形刚好组成一个半径是2的圆,根据圆面积公式计算总面积即可.
4.【答案】圆心角
【解析】【解答】在同一个圆中,扇形的大小与这个扇形的圆心角有关.
故答案为:圆心角.
【分析】在同一个圆中,扇形的大小与这个扇形的圆心角大小有关,圆心角越大,扇形越大,圆心角越小,扇形越小,据此解答.
5.【答案】 轴对称;一
【解析】【解答】解:扇形是轴对称图形,它有一条对称轴。
故答案为:轴对称;一。
【分析】扇形是轴对称图形,扇形只有一条对称轴,扇形的对称轴是圆心角的平分线所在的直线。
二、判断题
6.【答案】正确
【解析】【解答】解:根据分析可得:同一圆内圆心角的大小决定了扇形的大小,说法是正确的.故答案为:正确
【分析】同一个圆的半径是相等的,扇形的半径也相等,那么扇形面积就是由圆心角的大小决定的.
7.【答案】错误
【解析】【解答】缺少条件,在同一个圆内或等圆内,原题说法错误.
故答案为:错误.
【分析】在同一个圆内或等圆内,扇形的大小与圆心角的大小有关,圆心角大的扇形一定比圆心角小的扇形大,据此解答.
8.【答案】错误
【解析】【解答】解:计算扇形面积需要知道圆心角和半径,
不知道半径的大小,就无法计算面积,也就更不能比较面积大小了;
故答案为:错误.
【分析】计算扇形面积需要知道半径的大小和圆心角,只知道圆心角而不知道半径,则无法计算扇形的面积,也无法比较大小.
9.【答案】错误
【解析】【解答】解:扇形是圆的一部分,如果扇形的半径和圆的半径相等,那么扇形面积就小于圆的面积。原题说法错误。
故答案为:错误
【分析】扇形的面积比所在圆的面积小,原题没有说明半径的长短,所以无法确定面积的大小。
三、选择题
10.【答案】 B
【解析】【解答】解:设半圆的直径是d,
3.14×d÷2+d=10.28
? ? ?? 1.57d+d=10.28
??????????? 2.57d=10.28
?????????????????? d=4
半圆的面积:3.14×(4÷2)?×=3.14×2=6.28(m?)
故答案为:B
【分析】半圆的周长包括半圆弧的长度和一条直径的长度,因此设直径是d,然后根据周长列出一个方程,解方程求出直径,再根据圆面积公式计算半圆的面积即可.
11.【答案】 A
【解析】【解答】解:根据扇形的定义可知,?一条弧和经过这条弧两端的两条半径所围成的图形叫作扇形.
故答案为:A
【分析】扇形是圆的一部分,是一条弧和经过这条弧两端的两条半径所围成的图形;由此判断并选择即可.
12.【答案】C
【解析】【解答】根据分析可知,A、B图中都不是由半径和圆弧组成的,不是扇形,C图阴影部分是扇形.
故答案为:C.
【分析】根据扇形的定义:一条弧和经过这条弧两端的两条半径所围成的图形叫扇形,据此判断即可.
13.【答案】 B
【解析】【解答】解:π×6×2×
=π×12×
=4π
故答案为:B
【分析】扇形圆心角占360度的几分之几,扇形弧长就占所在圆周长的几分之几,由此计算扇形的弧长即可.
14.【答案】 C
【解析】【解答】解:根据圆心角的定义可知,顶点在圆心的角才叫圆心角.
故答案为:C
【分析】圆心角是顶点在圆心的角,圆心角的两条边是两条半径,由此判断并选择即可.
15.【答案】 B
【解析】【解答】根据分析可得,扇形的周长是:π×4×+4=π+4(厘米).
故答案为:B.
【分析】 把一张直径为4厘米的圆形纸片对折两次,得到的是一个圆心角是360°÷4=90°的扇形,这个扇形的周长是圆周长的+两条半径的长度,据此解答.
16.【答案】 B
【解析】【解答】 根据分析可知,圆锥的高h与扇形半径r之间的关系是:h<r.
故答案为:B.
【分析】根据题意,把该扇形围成圆锥后,扇形的半径即围成后圆锥的母线,圆锥的高与底面半径、圆锥母线构成直角三角形的三边,直角三角形中,斜边最长,所以扇形的高小于圆锥的母线(即扇形的半径r),据此判断即可.
四、解答题
17.【答案】 解:3.14×( )2× =12.56(平方厘米)
【解析】【分析】用平行四边形的面积除以底即可求出高,也就是圆的半径;阴影部分的面积是所在圆面积的, 根据圆面积公式计算阴影部分的面积即可。
18.【答案】 解:(3.14×42× )×2-4×4=9.12(m2)
答:两只羊都能吃到青草的面积是9.12平方米。
【解析】【分析】从图中可以看出,两只羊都能吃到青草的面积=圆的面积×2-正方形的面积,其中圆的面积=πr2 , 正方形的面积=边长×边长。
19.【答案】
【解析】【分析】根据圆心角和圆周角的定义作答即可。
20.【答案】
【解析】【分析】 弧和经过弧两端的半径所围成的图形叫做扇形。由此判断即可。
