高一数学人教A版必修4课件:第一章 三角函数 章末复习课 课件(共22张PPT)
文档属性
| 名称 | 高一数学人教A版必修4课件:第一章 三角函数 章末复习课 课件(共22张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-23 13:09:12 | ||
图片预览






文档简介
(共22张PPT)
章末复习课
第一章
三角函数
内容
索引
01
02
理网络
明结构
探题型
提能力
03
04
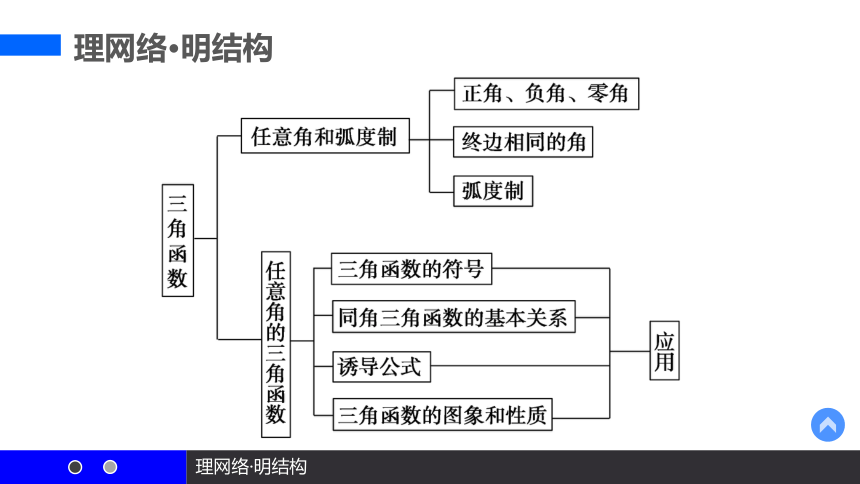
理网络·明结构
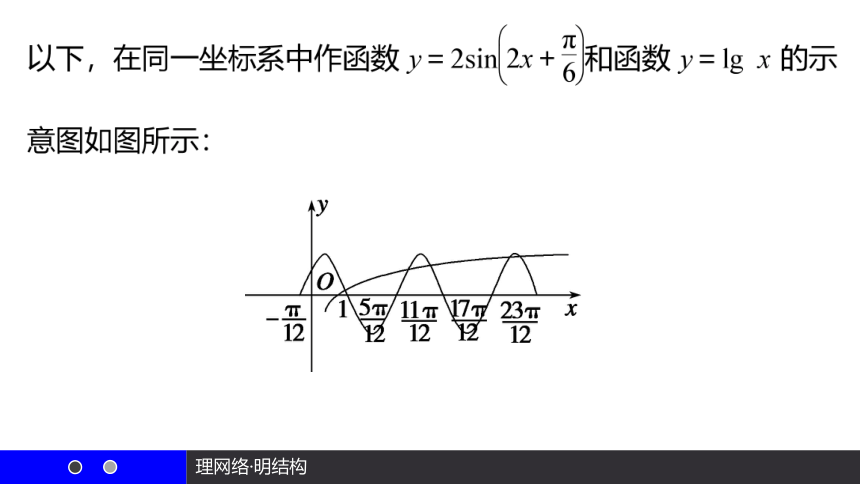
例1 已知函数f(x)=Asin(ωx+φ),x∈R(其中A>0,
ω>0,|φ|<)在一个周期内的简图如图所示,求函数
g(x)=f(x)-lg
x零点的个数.
探题型·提能力
题型一 数形结合思想在三角函数中的应用
解 显然A=2.
由图象过(0,1)点,则f(0)=1,即sin
φ=,
∴方程f(x)-lg
x=0共有实根63个.
∴函数g(x)=f(x)-lg
x共有63个零点.
反思与感悟 运用数形结合的思想化抽象为直观,使问题简单明了,数形结合在三角函数中有着广泛的应用.
跟踪训练1 若0x的大小关系是( )
A.2x>πsin
x
B.2x<πsin
x
C.2x=πsin
x
D.与x的取值有关
解析 在同一坐标平面内作出函数y=2x与函数y=πsin
x的图象,如图所示.
观察图象易知:
当x=0时,2x=πsin
x=0;
当x=时,2x=πsin
x=π;
而曲线y=πsin
x是上凸的.所以2x<πsin
x.故选B.
答案 B
例2
已知cos
θ=m,|m|≤1,求sin
θ、tan
θ的值.
题型二 分类讨论思想在三角函数求值中的应用
(2)当m=1时,θ=2kπ,k∈Z,sin
θ=tan
θ=0.
当m=-1时,θ=2kπ+π,k∈Z,sin
θ=tan
θ=0.
(3)当θ在第一、二象限时,
(4)当θ在第三、四象限时,
反思与感悟 已知角的某一个三角函数值为字母时,注意对字母是否为0、±1及分象限作讨论,讨论标准要统一.在三角函数部分,有不少题目都涉及到分类讨论的思想.
解析 ∵f(1)=e1-1=1,∴f(a)=1.
当a≥0时,f(a)=ea-1=1,
∴a-1=0,∴a=1;
当-1故选B.
答案 B
例3 已知函数f(x)=-sin2x-asin
x+b+1的最大值为0,最小值为-4,若实数a>0,求a、b的值.
解 令t=sin
x,则
题型三 转化与化归思想在三角函数中的应用
都不满足a的范围,舍去.
综上所述,a=2,b=-2.
反思与感悟 转化与化归的思想方法是数学中最基本的数学思想方法.数学中一切问题的解决都离不开转化与化归.上述解答将三角函数问题转化为熟悉的二次函数在闭区间上的最值问题.
跟踪训练3 已知定义在(-∞,3]上单调减函数f(x)使得f(1+sin2x)≤f(a-2cos
x)对一切实数x都成立,求a的取值范围.
解 根据题意,对一切x∈R都成立,有:
呈重点、现规律
三角函数的性质是本章复习的重点,在复习时,要充分利用数形结合思想把图象与性质结合起来,即利用图象的直观性得到函数的性质,或由单位圆中三角函数线表示的三角函数值来获得函数的性质,同时也能利用函数的性质来描述函数的图象,这样既有利于掌握函数的图象与性质,又能熟练运用数形结合的思想方法.
章末复习课
第一章
三角函数
内容
索引
01
02
理网络
明结构
探题型
提能力
03
04
理网络·明结构
例1 已知函数f(x)=Asin(ωx+φ),x∈R(其中A>0,
ω>0,|φ|<)在一个周期内的简图如图所示,求函数
g(x)=f(x)-lg
x零点的个数.
探题型·提能力
题型一 数形结合思想在三角函数中的应用
解 显然A=2.
由图象过(0,1)点,则f(0)=1,即sin
φ=,
∴方程f(x)-lg
x=0共有实根63个.
∴函数g(x)=f(x)-lg
x共有63个零点.
反思与感悟 运用数形结合的思想化抽象为直观,使问题简单明了,数形结合在三角函数中有着广泛的应用.
跟踪训练1 若0
A.2x>πsin
x
B.2x<πsin
x
C.2x=πsin
x
D.与x的取值有关
解析 在同一坐标平面内作出函数y=2x与函数y=πsin
x的图象,如图所示.
观察图象易知:
当x=0时,2x=πsin
x=0;
当x=时,2x=πsin
x=π;
而曲线y=πsin
x是上凸的.所以2x<πsin
x.故选B.
答案 B
例2
已知cos
θ=m,|m|≤1,求sin
θ、tan
θ的值.
题型二 分类讨论思想在三角函数求值中的应用
(2)当m=1时,θ=2kπ,k∈Z,sin
θ=tan
θ=0.
当m=-1时,θ=2kπ+π,k∈Z,sin
θ=tan
θ=0.
(3)当θ在第一、二象限时,
(4)当θ在第三、四象限时,
反思与感悟 已知角的某一个三角函数值为字母时,注意对字母是否为0、±1及分象限作讨论,讨论标准要统一.在三角函数部分,有不少题目都涉及到分类讨论的思想.
解析 ∵f(1)=e1-1=1,∴f(a)=1.
当a≥0时,f(a)=ea-1=1,
∴a-1=0,∴a=1;
当-1
答案 B
例3 已知函数f(x)=-sin2x-asin
x+b+1的最大值为0,最小值为-4,若实数a>0,求a、b的值.
解 令t=sin
x,则
题型三 转化与化归思想在三角函数中的应用
都不满足a的范围,舍去.
综上所述,a=2,b=-2.
反思与感悟 转化与化归的思想方法是数学中最基本的数学思想方法.数学中一切问题的解决都离不开转化与化归.上述解答将三角函数问题转化为熟悉的二次函数在闭区间上的最值问题.
跟踪训练3 已知定义在(-∞,3]上单调减函数f(x)使得f(1+sin2x)≤f(a-2cos
x)对一切实数x都成立,求a的取值范围.
解 根据题意,对一切x∈R都成立,有:
呈重点、现规律
三角函数的性质是本章复习的重点,在复习时,要充分利用数形结合思想把图象与性质结合起来,即利用图象的直观性得到函数的性质,或由单位圆中三角函数线表示的三角函数值来获得函数的性质,同时也能利用函数的性质来描述函数的图象,这样既有利于掌握函数的图象与性质,又能熟练运用数形结合的思想方法.
