22.1.2 二次函数y=ax2的图象和性质课件(23张PPT)
文档属性
| 名称 | 22.1.2 二次函数y=ax2的图象和性质课件(23张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-24 00:00:00 | ||
图片预览




文档简介
第二十二章 二次函数
22.1 二次函数的图象和性质
22.1.2二次函数y = ax 2 的图象和性质
2020年秋人教版数学九年级上册精品课件
学 习 目 标
3
1
2
在类比探究二次函数y = ax 2 的图象和性质的过程中,进一步体会研究函数图象和性质的基本方法和数形结合的思想.
了解抛物线的有关概念,会用描点法画出形如????=?????????2的二次函数的图象.
?
通过观察图象,掌握二次函数????=?????????2?的图象特征和性质.
?
1.一次函数的图象是一条 .
温故知新
3.二次函数的一般形式是什么?
????=?????????+????????+????(????,????,????是常数,????≠?0)
?
直线
列表,描点,连线
2.通常怎样画一个函数的图象?
知识讲解
…
0
1
2
3
…
…
…
9
4
1
0
1
9
4
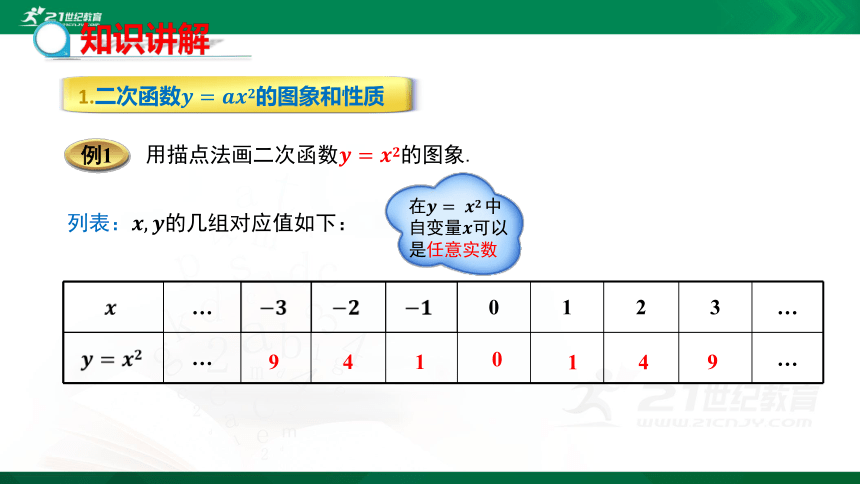
列表:????,????的几组对应值如下:
?
用描点法画二次函数????=????????的图象.
?
例1
1.二次函数????=????????????的图象和性质
?
在????=??????????中自变量????可以是任意实数
?
列表
描点
连线
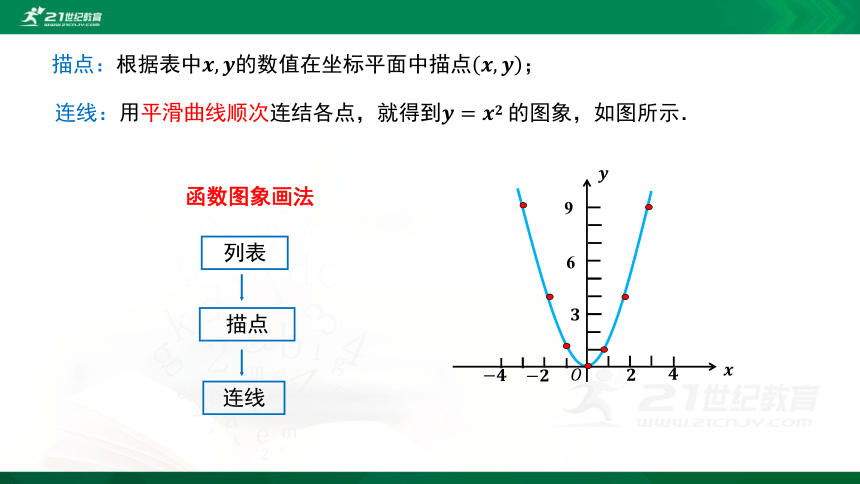
描点:根据表中????,????的数值在坐标平面中描点????,????;
?
连线:用平滑曲线顺次连结各点,就得到????=?????????的图象,如图所示.
?
????
?
????
?
?????
?
?????
?
????
?
????
?
6
9
????
?
????
?
函数图象画法
x
y
O
-4
-3
-2
-1
1
2
3
4
10
8
6
4
2
-2
y=x2
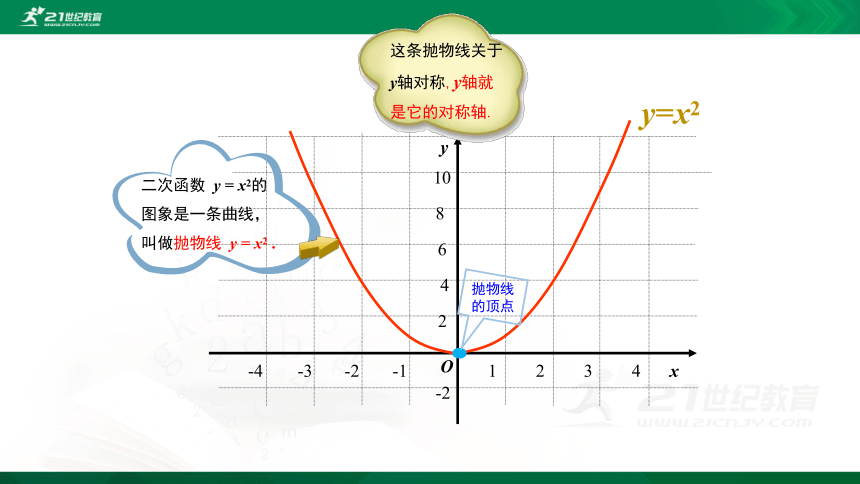
二次函数 y = x2的图象是一条曲线,叫做抛物线 y = x2 .
这条抛物线关于y轴对称,y轴就是它的对称轴.
抛物线的顶点
观察与思考
x
…
0
1
2
3
…
…
9
4
1
0
1
4
9
…
问题 从二次函数????=????????的图象你发现了什么性质?
?
在对称轴????轴的左侧,抛物线从左往右下降;
在对称轴????轴的右侧,抛物线从左往右上升.
?
顶点坐标是(0,0),是抛物线上的最低点.
????
?
????
?
?????
?
?????
?
????
?
????
?
6
9
????
?
????
?
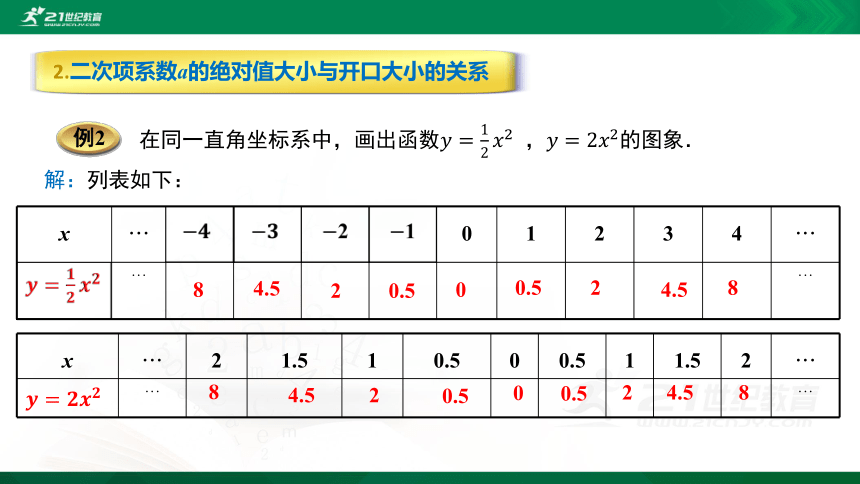
解:列表如下:
x
···
0
1
2
3
4
···
···
···
8
4.5
2
0.5
0
8
4.5
2
0.5
8
4.5
2
0.5
0
8
4.5
2
0.5
在同一直角坐标系中,画出函数????=12????2 ,????=2????2的图象.
?
2.二次项系数a的绝对值大小与开口大小的关系
例2
x
···
2
1.5
1
0.5
0
0.5
1
1.5
2
···
···
···
????=????????????
?
x
y
O
-2
2
2
4
6
4
-4
8
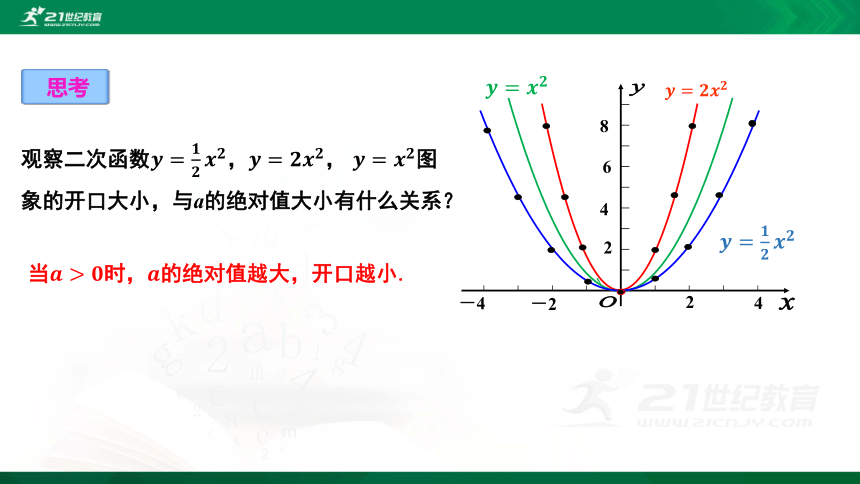
观察二次函数????=????????????????,????=????????????, ????=????????图象的开口大小,与a的绝对值大小有什么关系?
?
当????>????时,????的绝对值越大,开口越小.
?
????=????????????
?
????=????????
?
????=????????????????
?
思考
问题 请画出函数????=?????????的图象,观察图象函数????=?????????有哪些性质?
?
解:列表如下:
y
2
4
-2
-4
O
-3
-6
-9
x
在对称轴????轴的左侧,抛物线从左往右上升;
在对称轴????轴的右侧,抛物线从左往右下降.
?
顶点坐标是(0,0),是抛物线上的最高点.
x
…
-3
-2
-1
0
1
2
3
…
…
0
…
练一练:在同一直角坐标系中,画出函数 ????=?12????2 ,????=?2????2 的图象.
?
x
···
0
1
2
3
4
···
···
···
x
···
-2
-0.5
0
0.5
1
1.5
2
···
···
0
···
解:
列表如下:
x
y
O
-2
2
-2
-4
-6
4
-4
-8
观察二次函数????=????????????????? , ????=?????????,?????=?????????????图象的开口大小,与a的绝对值大小有什么关系?
?
当a<0时,a的绝对值越大,开口越小.
思考
????=?????????????
?
????=?????????
?
????=?????????????????
?
x
y
O
x
y
O
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
图象
位置与开口
对称性
顶点最值
增减性
总结
开口向上,在x轴上方
开口向下,在x轴下方
a的绝对值越大,开口越小
关于????轴对称,对称轴是直线????=0
?
顶点是原点(0,0)
当????=0时,????最小值=0
?
当????=0时,????最大值=0
?
在对称轴左侧递减,在对称轴右侧递增
在对称轴左侧递增,在对称轴右侧递减
问题 观察下列图象,抛物线????=????????????与????=?????????????(????>0)的关系是什么?
?
x
y
O
????=????????????
?
????=?????????????
?
3.抛物线????=????????????与????=?????????????的关系
?
二次项系数互为相反数,开口相反,大小相同,它们关于x轴对称.
4.函数????=????????????性质的应用
?
已知二次函数y=2x2.
(1)若点(-2,y1)与(3,y2)在此二次函数的图象上,则y1_____y2;(填“>”“=”或“<”)
(2)如图,此二次函数的图象经过点(0,0),长方形ABCD的顶点A、B在x轴上,C、D恰好在二次函数的图象上,若B点的横坐标为2,求图中阴影部分的面积之和.
例3
????1=8
?
????2=18
?
(1)把两点的横坐标代入二次函数解析式得纵坐标
分析:
<
二次函数图象关于y轴对称
<
图象左边部分与右边部分对称
(2)两个阴影部分面积相加等于右边第一象限内的矩形面积
(????,????)
?
(????,????)
?
8
点转换到同一侧
或
S阴影部分面积之和=????×????=????????
?
解:∵点B的坐标为(????,????),
∴当????=????时,????=????×????????=????.
∴点C的坐标为(????,????),????????=????.
∵抛物线和长方形都是轴对称图形,且y轴为它们的对称轴,
∴????????=????????,
∴在长方形????????????????内,左边阴影部分面积等于右边空白部分面积,
∴S阴影部分面积之和=????×????=????????.
?
求不规则图形的面积,常采用等面积割补法,将不规则图形转化为规则图形以方便求解.
二次函数y=ax2的图象关于y轴对称,因此对称轴左右两侧折叠可以重合,因此比较二次函数的大小时,我们可以根据图象的对称性转变到同一变化区域中(全部为升或全部为降),根据图象中函数值高低去比较.
归
纳
二次函数y=ax2的图象及性质
画法
描点法
以对称轴为中心对称取点
图象
抛物线
轴对称图形
性质
开口方向及大小
对称轴????轴
?
顶点坐标(0,0)
增减性
课堂小结
2.(1)????=????????????的图象是 ;
(2)????=????????????????的图象是 ;
(3)????=?????????????的图象是 ;
(4)????=?????????????????的图象是 .
?
1.已知二次函数????=????????的图象过点????,????,则它必过的另一点是( )
A. ????,????? B. ?????,???? C. ?????,????? D. ????,????
?
随堂训练
x
y
O
②
①
③
④
B
③
①
④
②
3.如图,观察函数????=(??????????)????????的图象,则k的取值范
围是 .
?
x
y
????>????
?
O
4.若抛物线????=?????????????(?????≠?????),过点(?????,????).
(1)则a的值是 ;
(2)对称轴是 ,开口 ;
(3)顶点坐标是 ,顶点是抛物线上的最 值,
抛物线在????轴的 方(除顶点外);
(4) 若????(????????,????????),????(????????,????????)在这条抛物线上,且?????????
2
y轴
向上
(0,0)
小
上
>
?
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
22.1 二次函数的图象和性质
22.1.2二次函数y = ax 2 的图象和性质
2020年秋人教版数学九年级上册精品课件
学 习 目 标
3
1
2
在类比探究二次函数y = ax 2 的图象和性质的过程中,进一步体会研究函数图象和性质的基本方法和数形结合的思想.
了解抛物线的有关概念,会用描点法画出形如????=?????????2的二次函数的图象.
?
通过观察图象,掌握二次函数????=?????????2?的图象特征和性质.
?
1.一次函数的图象是一条 .
温故知新
3.二次函数的一般形式是什么?
????=?????????+????????+????(????,????,????是常数,????≠?0)
?
直线
列表,描点,连线
2.通常怎样画一个函数的图象?
知识讲解
…
0
1
2
3
…
…
…
9
4
1
0
1
9
4
列表:????,????的几组对应值如下:
?
用描点法画二次函数????=????????的图象.
?
例1
1.二次函数????=????????????的图象和性质
?
在????=??????????中自变量????可以是任意实数
?
列表
描点
连线
描点:根据表中????,????的数值在坐标平面中描点????,????;
?
连线:用平滑曲线顺次连结各点,就得到????=?????????的图象,如图所示.
?
????
?
????
?
?????
?
?????
?
????
?
????
?
6
9
????
?
????
?
函数图象画法
x
y
O
-4
-3
-2
-1
1
2
3
4
10
8
6
4
2
-2
y=x2
二次函数 y = x2的图象是一条曲线,叫做抛物线 y = x2 .
这条抛物线关于y轴对称,y轴就是它的对称轴.
抛物线的顶点
观察与思考
x
…
0
1
2
3
…
…
9
4
1
0
1
4
9
…
问题 从二次函数????=????????的图象你发现了什么性质?
?
在对称轴????轴的左侧,抛物线从左往右下降;
在对称轴????轴的右侧,抛物线从左往右上升.
?
顶点坐标是(0,0),是抛物线上的最低点.
????
?
????
?
?????
?
?????
?
????
?
????
?
6
9
????
?
????
?
解:列表如下:
x
···
0
1
2
3
4
···
···
···
8
4.5
2
0.5
0
8
4.5
2
0.5
8
4.5
2
0.5
0
8
4.5
2
0.5
在同一直角坐标系中,画出函数????=12????2 ,????=2????2的图象.
?
2.二次项系数a的绝对值大小与开口大小的关系
例2
x
···
2
1.5
1
0.5
0
0.5
1
1.5
2
···
···
···
????=????????????
?
x
y
O
-2
2
2
4
6
4
-4
8
观察二次函数????=????????????????,????=????????????, ????=????????图象的开口大小,与a的绝对值大小有什么关系?
?
当????>????时,????的绝对值越大,开口越小.
?
????=????????????
?
????=????????
?
????=????????????????
?
思考
问题 请画出函数????=?????????的图象,观察图象函数????=?????????有哪些性质?
?
解:列表如下:
y
2
4
-2
-4
O
-3
-6
-9
x
在对称轴????轴的左侧,抛物线从左往右上升;
在对称轴????轴的右侧,抛物线从左往右下降.
?
顶点坐标是(0,0),是抛物线上的最高点.
x
…
-3
-2
-1
0
1
2
3
…
…
0
…
练一练:在同一直角坐标系中,画出函数 ????=?12????2 ,????=?2????2 的图象.
?
x
···
0
1
2
3
4
···
···
···
x
···
-2
-0.5
0
0.5
1
1.5
2
···
···
0
···
解:
列表如下:
x
y
O
-2
2
-2
-4
-6
4
-4
-8
观察二次函数????=????????????????? , ????=?????????,?????=?????????????图象的开口大小,与a的绝对值大小有什么关系?
?
当a<0时,a的绝对值越大,开口越小.
思考
????=?????????????
?
????=?????????
?
????=?????????????????
?
x
y
O
x
y
O
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
图象
位置与开口
对称性
顶点最值
增减性
总结
开口向上,在x轴上方
开口向下,在x轴下方
a的绝对值越大,开口越小
关于????轴对称,对称轴是直线????=0
?
顶点是原点(0,0)
当????=0时,????最小值=0
?
当????=0时,????最大值=0
?
在对称轴左侧递减,在对称轴右侧递增
在对称轴左侧递增,在对称轴右侧递减
问题 观察下列图象,抛物线????=????????????与????=?????????????(????>0)的关系是什么?
?
x
y
O
????=????????????
?
????=?????????????
?
3.抛物线????=????????????与????=?????????????的关系
?
二次项系数互为相反数,开口相反,大小相同,它们关于x轴对称.
4.函数????=????????????性质的应用
?
已知二次函数y=2x2.
(1)若点(-2,y1)与(3,y2)在此二次函数的图象上,则y1_____y2;(填“>”“=”或“<”)
(2)如图,此二次函数的图象经过点(0,0),长方形ABCD的顶点A、B在x轴上,C、D恰好在二次函数的图象上,若B点的横坐标为2,求图中阴影部分的面积之和.
例3
????1=8
?
????2=18
?
(1)把两点的横坐标代入二次函数解析式得纵坐标
分析:
<
二次函数图象关于y轴对称
<
图象左边部分与右边部分对称
(2)两个阴影部分面积相加等于右边第一象限内的矩形面积
(????,????)
?
(????,????)
?
8
点转换到同一侧
或
S阴影部分面积之和=????×????=????????
?
解:∵点B的坐标为(????,????),
∴当????=????时,????=????×????????=????.
∴点C的坐标为(????,????),????????=????.
∵抛物线和长方形都是轴对称图形,且y轴为它们的对称轴,
∴????????=????????,
∴在长方形????????????????内,左边阴影部分面积等于右边空白部分面积,
∴S阴影部分面积之和=????×????=????????.
?
求不规则图形的面积,常采用等面积割补法,将不规则图形转化为规则图形以方便求解.
二次函数y=ax2的图象关于y轴对称,因此对称轴左右两侧折叠可以重合,因此比较二次函数的大小时,我们可以根据图象的对称性转变到同一变化区域中(全部为升或全部为降),根据图象中函数值高低去比较.
归
纳
二次函数y=ax2的图象及性质
画法
描点法
以对称轴为中心对称取点
图象
抛物线
轴对称图形
性质
开口方向及大小
对称轴????轴
?
顶点坐标(0,0)
增减性
课堂小结
2.(1)????=????????????的图象是 ;
(2)????=????????????????的图象是 ;
(3)????=?????????????的图象是 ;
(4)????=?????????????????的图象是 .
?
1.已知二次函数????=????????的图象过点????,????,则它必过的另一点是( )
A. ????,????? B. ?????,???? C. ?????,????? D. ????,????
?
随堂训练
x
y
O
②
①
③
④
B
③
①
④
②
3.如图,观察函数????=(??????????)????????的图象,则k的取值范
围是 .
?
x
y
????>????
?
O
4.若抛物线????=?????????????(?????≠?????),过点(?????,????).
(1)则a的值是 ;
(2)对称轴是 ,开口 ;
(3)顶点坐标是 ,顶点是抛物线上的最 值,
抛物线在????轴的 方(除顶点外);
(4) 若????(????????,????????),????(????????,????????)在这条抛物线上,且?????????
2
y轴
向上
(0,0)
小
上
>
?
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
同课章节目录
