22.1.4.2 用待定系数法求二次函数的解析式课件(17张PPT)
文档属性
| 名称 | 22.1.4.2 用待定系数法求二次函数的解析式课件(17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-24 00:00:00 | ||
图片预览






文档简介
第二十二章 二次函数
22.1 二次函数的图象和性质
22.1.4 二次函数y=ax2+bx+c的图象和性质
第2课时 用待定系数法求二次函数的解析式
2020年秋人教版数学九年级上册精品课件
学 习 目 标
1
2
会用待定系数法求二次函数的解析式.
会根据题中条件选择合适的方法求二次函数的解析式.
1.一次函数????=????????+????(????≠????)有几个待定系数?通常需要已知几个点的坐标求出它的解析式?
?
2.求一次函数解析式的方法是什么?它的一般步骤是什么?
待定系数法
(1)设:设出解析式????=????????+????;
(2)代:代入2对????、????的对应值;
(3)解:解所得的方程组;
(4)写:将求得的????、????的值代入,写出函数解析式;
?
温故知新
2个
2个
探究归纳
思考1 :(1)二次函数????=????????????+????????+????(????≠????)中有几个待定系数?需要几个抛物线上的点的坐标才能求出来?
?
(2)下面是二次函数????=????????????+????????+????的图象上点的横坐标????、纵坐标????的一部分对应值:
?
x
0
1
2
3
y
0
0
知识讲解
3个
3个
1.一般式(三点式)法求二次函数的解析式
解: 设这个二次函数的解析式是????=????????????+????????+????,把(?????,?????),(0,?????),(2,0)代入????=????????????+????????+????,得
?
①选取(?????,?????),(0,?????),(2,0),试求出这个二
次函数的解析式.
?
∴ 所求的二次函数的解析式是????=????????????????+?????4.
?
待定系数法步骤:
1.设:解析式
2.代:????、????的
值代入
3.解:方程组
4.写:写出解
析式
?
?????????????????+????=?????,????=?????,????????+????????+????=????
?
解得????=????????,????=????,????=?????,
?
?
一般式(三点式)法求二次函数解析式的方法
x
0
1
2
3
y
0
0
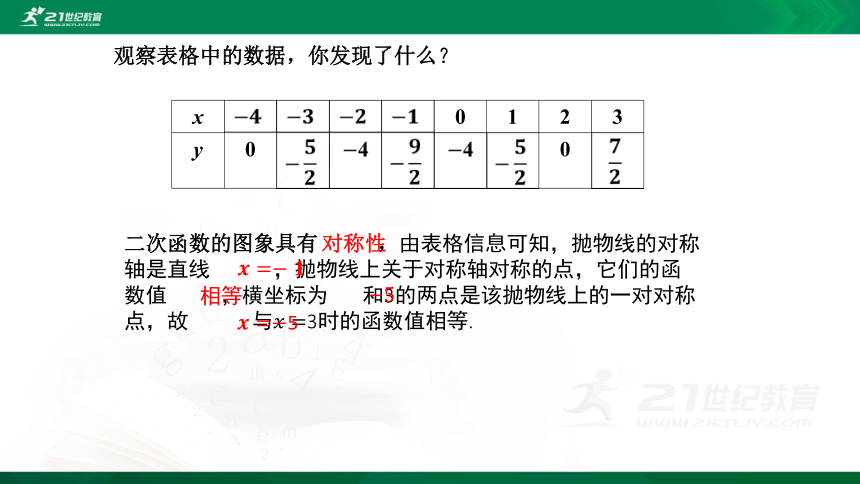
二次函数的图象具有 ,由表格信息可知,抛物线的对称轴是直线 ,抛物线上关于对称轴对称的点,它们的函数值 ,横坐标为 和3的两点是该抛物线上的一对对称点,故 与????=3时的函数值相等.
?
对称性
????=?????
?
相等
?5
?
????=?5
?
观察表格中的数据,你发现了什么?
选取顶点?????,?????????和点(????,?????),试求出
这个二次函数的解析式.
?
设这个二次函数的解析式是????=????(?????????)????+????,
把顶点?????,?????????代入????=????(?????????)????+????,得????=????????+??????????????????,
?
再把点(????,?????)代入上式,得
?
????(????+????)?????????????=?4,
?
解得???? =????????.
?
∴所求的二次函数的解析式是????=????????(????+????)?????????????.
?
2.顶点式法求二次函数的解析式
x
0
1
2
3
y
0
0
解:
顶点式法求二次函数解析式的方法
知道抛物线的顶点坐标,求解析式的方法叫做顶点式法.
①设函数解析式是????=????(?????????)????+????;
②先代入顶点坐标,得到关于a的一元一次方程;
③将另一点的坐标代入关于????的一元一次方程求出????值;
④根据求得的????值写出函数解析式.
?
步骤:
解:∵ (?????,????),(2,0)是抛物线????=????????????+????????+????与????轴的交点,
∴可设这个二次函数的解析式是????=????(?????????????)(?????????????).
?
????=????(????+????)(?????????).
?
再把点(0,?4)代入上式,得
?
????????+?????????????=?????,
?
解得????= ?????????,
?
∴所求的二次函数的解析式是????=????????(????+????)(?????????),即????=????????????????+?????4.
?
选取(?????,????),(2,0),(????,?????),试求出这个二次函数的解析式.
?
3. 交点式法求二次函数的解析式
x
0
1
2
3
y
0
0
其中????????、????????为交点的横坐标
?
因此
交点式法求二次函数解析式的方法
知道抛物线与x轴的交点坐标,求解析式的方法叫做交点式法.
①设函数解析式是????=????(?????????????)(?????????????);
②先把两交点的横坐标????????、????????代入,得到关于a的一元一次方程;
③将抛物线上另一点的坐标代入求出a的值;
④根据求得的a的值写出函数解析式.
?
步骤:
①已知任意三点坐标
②已知顶点坐标或对称轴或最值
③已知抛物线与????轴的两个交点
?
已知条件
所选方法
一般式法:????=????????????+????????+????
?
顶点式法:????=????(?????????)????+????
?
交点式法:????=????(?????????????)(?????????????)?(x1、x2为交点的横坐标)
?
待定系数法
求二次函数解析式
课堂小结
1.已知二次函数????=????????????+????????+????,当????=?????时,函数值是?????;当????=????时,函数值是5,则此二次函数的解析式为( )
A.????=????????????+????????????? B.????=????????+?????????????
C.????=?????????????+????????+???? D.????=????????????+????????+????
?
随堂训练
2. 二次函数的部分图象如图所示,对称轴是????=?????时,则这个二次函数的解析式为( )
A.????=?????????+????????+????? ?????????B.????=????????+????????+????
C.????=?????????+????????????? D.????=??????????????????+????
?
A
D
3. 过(?????,????)、(????,????)、(????,????)三点的抛物线的解析式
是 .
?
????=??????????????????????+????
?
4.已知二次函数????=?????????+????????+????(????,????均为常数)的图象经过两
点????(????,????),????(????,?????).
(1)求这个二次函数的解析式;
(2)若点????(????,????)(????>????)在这个二次函数的图象上,连接
????????,????????,求△????????????的面积
?
????=?????????+?????????6
?
△????????????的面积为3
?
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
22.1 二次函数的图象和性质
22.1.4 二次函数y=ax2+bx+c的图象和性质
第2课时 用待定系数法求二次函数的解析式
2020年秋人教版数学九年级上册精品课件
学 习 目 标
1
2
会用待定系数法求二次函数的解析式.
会根据题中条件选择合适的方法求二次函数的解析式.
1.一次函数????=????????+????(????≠????)有几个待定系数?通常需要已知几个点的坐标求出它的解析式?
?
2.求一次函数解析式的方法是什么?它的一般步骤是什么?
待定系数法
(1)设:设出解析式????=????????+????;
(2)代:代入2对????、????的对应值;
(3)解:解所得的方程组;
(4)写:将求得的????、????的值代入,写出函数解析式;
?
温故知新
2个
2个
探究归纳
思考1 :(1)二次函数????=????????????+????????+????(????≠????)中有几个待定系数?需要几个抛物线上的点的坐标才能求出来?
?
(2)下面是二次函数????=????????????+????????+????的图象上点的横坐标????、纵坐标????的一部分对应值:
?
x
0
1
2
3
y
0
0
知识讲解
3个
3个
1.一般式(三点式)法求二次函数的解析式
解: 设这个二次函数的解析式是????=????????????+????????+????,把(?????,?????),(0,?????),(2,0)代入????=????????????+????????+????,得
?
①选取(?????,?????),(0,?????),(2,0),试求出这个二
次函数的解析式.
?
∴ 所求的二次函数的解析式是????=????????????????+?????4.
?
待定系数法步骤:
1.设:解析式
2.代:????、????的
值代入
3.解:方程组
4.写:写出解
析式
?
?????????????????+????=?????,????=?????,????????+????????+????=????
?
解得????=????????,????=????,????=?????,
?
?
一般式(三点式)法求二次函数解析式的方法
x
0
1
2
3
y
0
0
二次函数的图象具有 ,由表格信息可知,抛物线的对称轴是直线 ,抛物线上关于对称轴对称的点,它们的函数值 ,横坐标为 和3的两点是该抛物线上的一对对称点,故 与????=3时的函数值相等.
?
对称性
????=?????
?
相等
?5
?
????=?5
?
观察表格中的数据,你发现了什么?
选取顶点?????,?????????和点(????,?????),试求出
这个二次函数的解析式.
?
设这个二次函数的解析式是????=????(?????????)????+????,
把顶点?????,?????????代入????=????(?????????)????+????,得????=????????+??????????????????,
?
再把点(????,?????)代入上式,得
?
????(????+????)?????????????=?4,
?
解得???? =????????.
?
∴所求的二次函数的解析式是????=????????(????+????)?????????????.
?
2.顶点式法求二次函数的解析式
x
0
1
2
3
y
0
0
解:
顶点式法求二次函数解析式的方法
知道抛物线的顶点坐标,求解析式的方法叫做顶点式法.
①设函数解析式是????=????(?????????)????+????;
②先代入顶点坐标,得到关于a的一元一次方程;
③将另一点的坐标代入关于????的一元一次方程求出????值;
④根据求得的????值写出函数解析式.
?
步骤:
解:∵ (?????,????),(2,0)是抛物线????=????????????+????????+????与????轴的交点,
∴可设这个二次函数的解析式是????=????(?????????????)(?????????????).
?
????=????(????+????)(?????????).
?
再把点(0,?4)代入上式,得
?
????????+?????????????=?????,
?
解得????= ?????????,
?
∴所求的二次函数的解析式是????=????????(????+????)(?????????),即????=????????????????+?????4.
?
选取(?????,????),(2,0),(????,?????),试求出这个二次函数的解析式.
?
3. 交点式法求二次函数的解析式
x
0
1
2
3
y
0
0
其中????????、????????为交点的横坐标
?
因此
交点式法求二次函数解析式的方法
知道抛物线与x轴的交点坐标,求解析式的方法叫做交点式法.
①设函数解析式是????=????(?????????????)(?????????????);
②先把两交点的横坐标????????、????????代入,得到关于a的一元一次方程;
③将抛物线上另一点的坐标代入求出a的值;
④根据求得的a的值写出函数解析式.
?
步骤:
①已知任意三点坐标
②已知顶点坐标或对称轴或最值
③已知抛物线与????轴的两个交点
?
已知条件
所选方法
一般式法:????=????????????+????????+????
?
顶点式法:????=????(?????????)????+????
?
交点式法:????=????(?????????????)(?????????????)?(x1、x2为交点的横坐标)
?
待定系数法
求二次函数解析式
课堂小结
1.已知二次函数????=????????????+????????+????,当????=?????时,函数值是?????;当????=????时,函数值是5,则此二次函数的解析式为( )
A.????=????????????+????????????? B.????=????????+?????????????
C.????=?????????????+????????+???? D.????=????????????+????????+????
?
随堂训练
2. 二次函数的部分图象如图所示,对称轴是????=?????时,则这个二次函数的解析式为( )
A.????=?????????+????????+????? ?????????B.????=????????+????????+????
C.????=?????????+????????????? D.????=??????????????????+????
?
A
D
3. 过(?????,????)、(????,????)、(????,????)三点的抛物线的解析式
是 .
?
????=??????????????????????+????
?
4.已知二次函数????=?????????+????????+????(????,????均为常数)的图象经过两
点????(????,????),????(????,?????).
(1)求这个二次函数的解析式;
(2)若点????(????,????)(????>????)在这个二次函数的图象上,连接
????????,????????,求△????????????的面积
?
????=?????????+?????????6
?
△????????????的面积为3
?
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
同课章节目录
