22.1.3.1 二次函数y=ax2+k的图象和性质课件(16张PPT)
文档属性
| 名称 | 22.1.3.1 二次函数y=ax2+k的图象和性质课件(16张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-24 07:07:20 | ||
图片预览


文档简介
第二十二章 二次函数
22.1 二次函数的图象和性质
2020年秋人教版数学九年级上册精品课件
?
第1课时 二次函数y=ax2+k的图象和性质
学 习 目 标
3
1
2
探究二次函数y = ax 2与y=ax2+k的联系.
能够画出二次函数y=ax2+k的图象.
?
通过观察图象,掌握二次函数y=ax2+k的图象特征和性质.(重点)
?
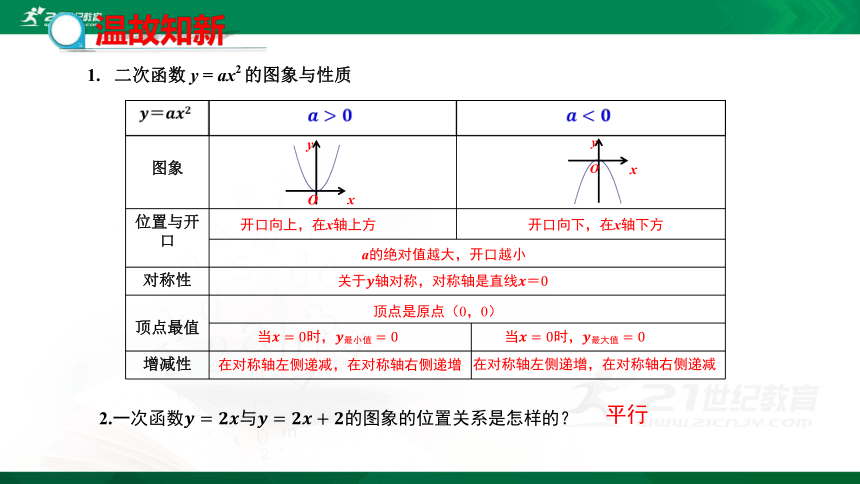
温故知新
1. 二次函数 y = ax2 的图象与性质
x
y
O
x
y
O
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
图象
位置与开口
对称性
顶点最值
增减性
开口向上,在x轴上方
开口向下,在x轴下方
a的绝对值越大,开口越小
关于????轴对称,对称轴是直线????=0
?
顶点是原点(0,0)
当????=0时,????最小值=0
?
当????=0时,????最大值=0
?
在对称轴左侧递减,在对称轴右侧递增
在对称轴左侧递增,在对称轴右侧递减
2.一次函数????=????????与????=????????+????的图象的位置关系是怎样的?
?
平行
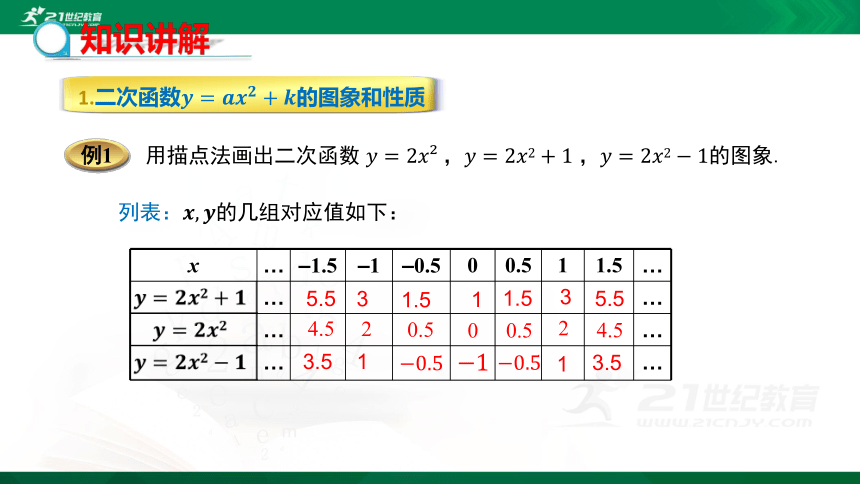
知识讲解
列表:????,????的几组对应值如下:
?
用描点法画出二次函数 ????=2??????,????=2????2+1 ,????=2????2?1的图象.
?
例1
1.二次函数????=????????????+????的图象和性质
?
x
…
–1.5
–1
–0.5
0
0.5
1
1.5
…
…
…
…
…
…
…
3.5
1
?0.5
?
1
?0.5
?
?1
?
3.5
5.5
1.5
3
1.5
1
3
5.5
4.5
2
0.5
0
0.5
2
4.5
????
?
????
?
?????
?
????
?
????
?
6
????
?
????
?
????=????????????+????
?
????=?????????????????
?
????=????????????
?
?????
?
????
?
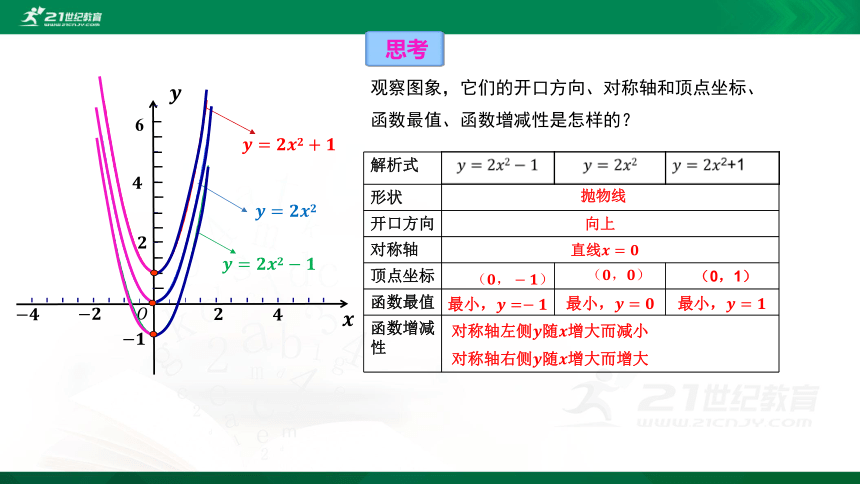
观察图象,它们的开口方向、对称轴和顶点坐标、函数最值、函数增减性是怎样的?
思考
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}解析式
形状
开口方向
对称轴
顶点坐标
函数最值
函数增减性
抛物线
向上
(????,?????)
?
(????,????)
?
(0,1)
直线????=????
?
最小,????=?????
?
最小,????=????
?
最小,????=????
?
对称轴右侧????随????增大而增大
?
对称轴左侧????随????增大而减小
?
?????
?
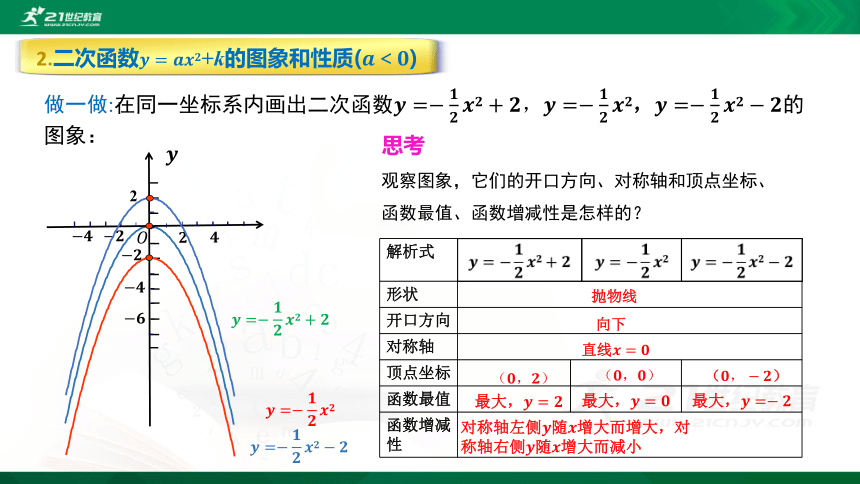
做一做:在同一坐标系内画出二次函数????=?????????????????+????,????=?????????????????,????=??????????????????????的图象:
?
????=?????????????????+????
?
????=?????????????????
?
????=??????????????????????
?
2.二次函数????=????????????+k的图象和性质(????<????)
?
????
?
????
?
?????
?
????
?
????
?
2
?????
?
?????
?
?????
?
?????
?
观察图象,它们的开口方向、对称轴和顶点坐标、函数最值、函数增减性是怎样的?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}解析式
形状
开口方向
对称轴
顶点坐标
函数最值
函数增减性
抛物线
向下
(????,????)
?
(????,????)
?
(????,?????)
?
直线????=????
?
最大,????=????
?
最大,????=????
?
最大,????=?????
?
对称轴左侧????随????增大而增大,对称轴右侧????随????增大而减小
?
思考
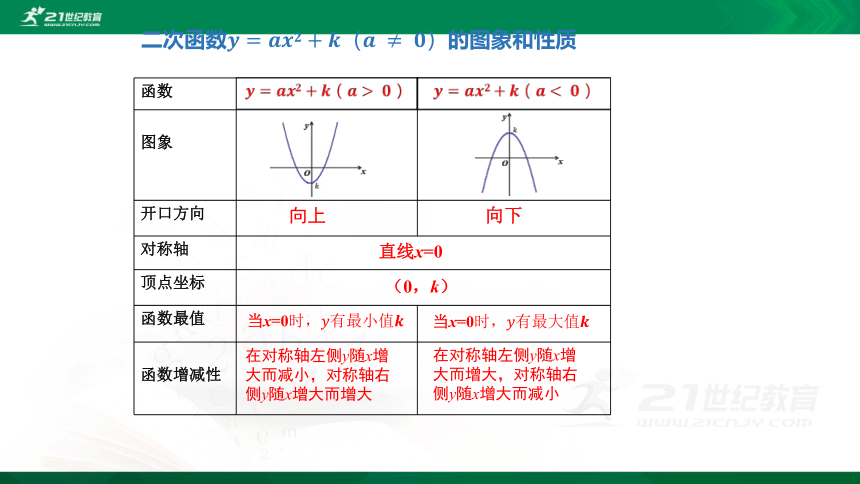
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}函数
图象
开口方向
对称轴
顶点坐标
函数最值
函数增减性
向上
直线x=0
向下
在对称轴左侧y随x增大而减小,对称轴右侧y随x增大而增大
(0,k)
二次函数????=????????????+????(?????≠?????)的图象和性质
?
在对称轴左侧y随x增大而增大,对称轴右侧y随x增大而减小
当x=0时,????有最大值????
?
当x=0时,????有最小值????
?
已知不重合的两点(????1,????1),(????2,????2)均在抛物线????=????2?1上,
下列说法正确的是( )
A.若????1= ????2,则????1=????2 B.若????1=?????2, 则????1= ?????2
C.若0????2 D.若?????1????2
?
例2
x
y
O
关于y轴对称,开口向上
若????1= ????2,
?
若????1=?????2,
?
若0?
则????1?
若?????1?
则????1>????2.
?
解析:
则????1=????2 或????1=?????2 .
?
则????1= ????2.
?
3.二次函数y=ax2+k的图象的平移
????=???????????? 向___平移___个单位长度得到抛物线????=????????????+????.
?
????=???????????? 向___平移 个单位长度得到抛物线????=?????????????????.
?
下
5
3
2
1
?6
?
-4
-2
2
4
4
????
?
-1
????
?
????
?
????=????????????+????
?
????=????????????
?
????=?????????????????
?
思考
上
????=????????????
?
????=????????????+????
?
????=?????????????????
?
+????
?
?????
?
1
1
思考 二次函数????=????????2 与????=????????2+????(?????≠?0)的图象有什么关系?
?
当k < 0 时,向下平移?????个单位长度得到.
?
二次函数y=ax2+k的图象可以由 y=ax2 的图象平移得到:
当k > 0 时,向上平移k个单位长度得到;
规律:上加下减
二次函数????=????????????+????的图象及性质
?
图象
抛物线
轴对称图形
性质
开口方向
对称轴:????轴
?
顶点坐标:(0,????)
?
增减性
课堂小结
与y=ax2的关系
????正向上平移
?
????负向下平移
?
随堂训练
1.填表:
函数
开口方向
顶点坐标
对称轴
有最高(低)点
向下
向上
向下
(????,????)
?
(????,????)
?
(????,?????)
?
y轴
y轴
y轴
有最高点
有最低点
有最高点
2.抛物线?????=? ????????x2+2的顶点坐标是 ,对称轴是 ,在对称轴的左侧,????随????的增大而 ;当????= ?时,????有最 值是 .它可以由抛物线?????=? ????????x2向 平移 个单位得到.
?
(????,????)
?
y轴
增大
????
?
大
????
?
上
?
????
?
3.已知二次函数????=?????????????????的图象经过点(1,-1),则这个二次函数的解析式为 .
4.从????=?????????????3的图象上可以看出,当?????≤????≤????时,????的取值范围是 .
5.在同一坐标系中,函数????=????????????+????与????=????????+????的图象的相对位置可以是( )
?
A
????
?
O
A
????
?
????
?
????
?
C
O
D
????
?
????
?
O
????
?
????
?
B
O
6.已知二次函数????=????????????+????,当x取????????,????????(????????≠????????)时,函数值相等,则当x=x1+x2时,其函数值为________.
?
????
?
????=?????????????
?
?????≤????≤????
?
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
22.1 二次函数的图象和性质
2020年秋人教版数学九年级上册精品课件
?
第1课时 二次函数y=ax2+k的图象和性质
学 习 目 标
3
1
2
探究二次函数y = ax 2与y=ax2+k的联系.
能够画出二次函数y=ax2+k的图象.
?
通过观察图象,掌握二次函数y=ax2+k的图象特征和性质.(重点)
?
温故知新
1. 二次函数 y = ax2 的图象与性质
x
y
O
x
y
O
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
图象
位置与开口
对称性
顶点最值
增减性
开口向上,在x轴上方
开口向下,在x轴下方
a的绝对值越大,开口越小
关于????轴对称,对称轴是直线????=0
?
顶点是原点(0,0)
当????=0时,????最小值=0
?
当????=0时,????最大值=0
?
在对称轴左侧递减,在对称轴右侧递增
在对称轴左侧递增,在对称轴右侧递减
2.一次函数????=????????与????=????????+????的图象的位置关系是怎样的?
?
平行
知识讲解
列表:????,????的几组对应值如下:
?
用描点法画出二次函数 ????=2??????,????=2????2+1 ,????=2????2?1的图象.
?
例1
1.二次函数????=????????????+????的图象和性质
?
x
…
–1.5
–1
–0.5
0
0.5
1
1.5
…
…
…
…
…
…
…
3.5
1
?0.5
?
1
?0.5
?
?1
?
3.5
5.5
1.5
3
1.5
1
3
5.5
4.5
2
0.5
0
0.5
2
4.5
????
?
????
?
?????
?
????
?
????
?
6
????
?
????
?
????=????????????+????
?
????=?????????????????
?
????=????????????
?
?????
?
????
?
观察图象,它们的开口方向、对称轴和顶点坐标、函数最值、函数增减性是怎样的?
思考
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}解析式
形状
开口方向
对称轴
顶点坐标
函数最值
函数增减性
抛物线
向上
(????,?????)
?
(????,????)
?
(0,1)
直线????=????
?
最小,????=?????
?
最小,????=????
?
最小,????=????
?
对称轴右侧????随????增大而增大
?
对称轴左侧????随????增大而减小
?
?????
?
做一做:在同一坐标系内画出二次函数????=?????????????????+????,????=?????????????????,????=??????????????????????的图象:
?
????=?????????????????+????
?
????=?????????????????
?
????=??????????????????????
?
2.二次函数????=????????????+k的图象和性质(????<????)
?
????
?
????
?
?????
?
????
?
????
?
2
?????
?
?????
?
?????
?
?????
?
观察图象,它们的开口方向、对称轴和顶点坐标、函数最值、函数增减性是怎样的?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}解析式
形状
开口方向
对称轴
顶点坐标
函数最值
函数增减性
抛物线
向下
(????,????)
?
(????,????)
?
(????,?????)
?
直线????=????
?
最大,????=????
?
最大,????=????
?
最大,????=?????
?
对称轴左侧????随????增大而增大,对称轴右侧????随????增大而减小
?
思考
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}函数
图象
开口方向
对称轴
顶点坐标
函数最值
函数增减性
向上
直线x=0
向下
在对称轴左侧y随x增大而减小,对称轴右侧y随x增大而增大
(0,k)
二次函数????=????????????+????(?????≠?????)的图象和性质
?
在对称轴左侧y随x增大而增大,对称轴右侧y随x增大而减小
当x=0时,????有最大值????
?
当x=0时,????有最小值????
?
已知不重合的两点(????1,????1),(????2,????2)均在抛物线????=????2?1上,
下列说法正确的是( )
A.若????1= ????2,则????1=????2 B.若????1=?????2, 则????1= ?????2
C.若0????2 D.若?????1????2
?
例2
x
y
O
关于y轴对称,开口向上
若????1= ????2,
?
若????1=?????2,
?
若0?
则????1?
若?????1?
则????1>????2.
?
解析:
则????1=????2 或????1=?????2 .
?
则????1= ????2.
?
3.二次函数y=ax2+k的图象的平移
????=???????????? 向___平移___个单位长度得到抛物线????=????????????+????.
?
????=???????????? 向___平移 个单位长度得到抛物线????=?????????????????.
?
下
5
3
2
1
?6
?
-4
-2
2
4
4
????
?
-1
????
?
????
?
????=????????????+????
?
????=????????????
?
????=?????????????????
?
思考
上
????=????????????
?
????=????????????+????
?
????=?????????????????
?
+????
?
?????
?
1
1
思考 二次函数????=????????2 与????=????????2+????(?????≠?0)的图象有什么关系?
?
当k < 0 时,向下平移?????个单位长度得到.
?
二次函数y=ax2+k的图象可以由 y=ax2 的图象平移得到:
当k > 0 时,向上平移k个单位长度得到;
规律:上加下减
二次函数????=????????????+????的图象及性质
?
图象
抛物线
轴对称图形
性质
开口方向
对称轴:????轴
?
顶点坐标:(0,????)
?
增减性
课堂小结
与y=ax2的关系
????正向上平移
?
????负向下平移
?
随堂训练
1.填表:
函数
开口方向
顶点坐标
对称轴
有最高(低)点
向下
向上
向下
(????,????)
?
(????,????)
?
(????,?????)
?
y轴
y轴
y轴
有最高点
有最低点
有最高点
2.抛物线?????=? ????????x2+2的顶点坐标是 ,对称轴是 ,在对称轴的左侧,????随????的增大而 ;当????= ?时,????有最 值是 .它可以由抛物线?????=? ????????x2向 平移 个单位得到.
?
(????,????)
?
y轴
增大
????
?
大
????
?
上
?
????
?
3.已知二次函数????=?????????????????的图象经过点(1,-1),则这个二次函数的解析式为 .
4.从????=?????????????3的图象上可以看出,当?????≤????≤????时,????的取值范围是 .
5.在同一坐标系中,函数????=????????????+????与????=????????+????的图象的相对位置可以是( )
?
A
????
?
O
A
????
?
????
?
????
?
C
O
D
????
?
????
?
O
????
?
????
?
B
O
6.已知二次函数????=????????????+????,当x取????????,????????(????????≠????????)时,函数值相等,则当x=x1+x2时,其函数值为________.
?
????
?
????=?????????????
?
?????≤????≤????
?
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
同课章节目录
