22.2 二次函数与一元二次方程课件(21张PPT)
文档属性
| 名称 | 22.2 二次函数与一元二次方程课件(21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-24 00:00:00 | ||
图片预览




文档简介
第二十二章 二次函数
22.2 二次函数与一元二次方程
2020年秋人教版数学九年级上册精品课件
学 习 目 标
3
1
2
了解用图象法求一元二次方程的近似根.
通过探索,理解二次函数与一元二次方程之间的联系.
能运用二次函数的图象与性质确定方程的解.
情景导入
问题:如图,以 40 m /s的速度将小球沿与地面成 30°角的方向击出时,小球的飞行路线是一条抛物线.如果不考虑空气阻力,小球的飞行高度h(单位:m)与飞行时间 ???? (单位:s)之间具有函数关系:h=?20??????–?5?????2???.
?
知识讲解
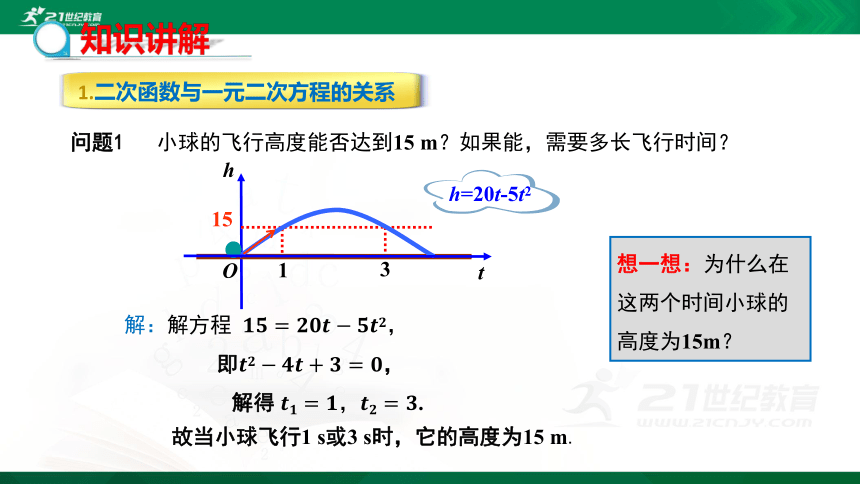
问题1 小球的飞行高度能否达到15 m?如果能,需要多长飞行时间?
1.二次函数与一元二次方程的关系
O
h
t
15
1
3
故当小球飞行1 s或3 s时,它的高度为15 m.
解:解方程 ????????=?????????????????????????,
即?????????????????+????=????,
解得 ????????=????,????????=????.
?
h=20t-5t2
想一想:为什么在这两个时间小球的高度为15m?
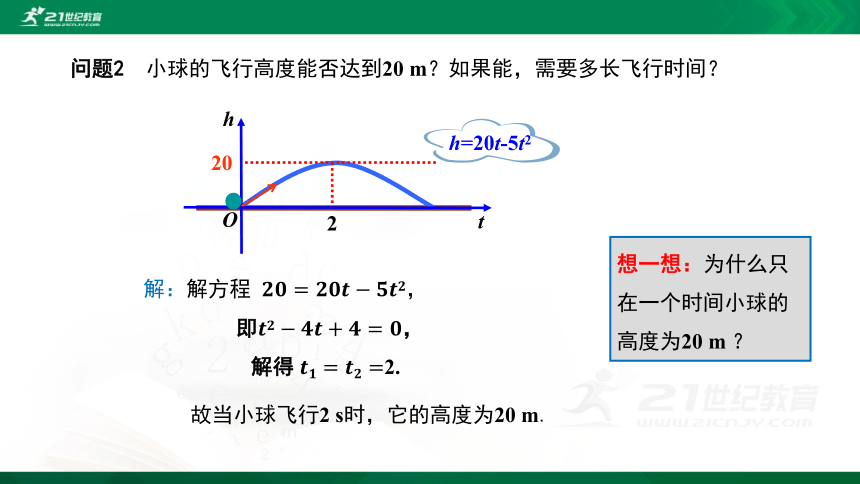
问题2 小球的飞行高度能否达到20 m?如果能,需要多长飞行时间?
O
h
t
20
2
故当小球飞行2 s时,它的高度为20 m.
解:解方程 ????????=?????????????????????????,
即?????????????????+????=????,
解得 ????????=????????=2.
?
h=20t-5t2
想一想:为什么只在一个时间小球的高度为20 m ?
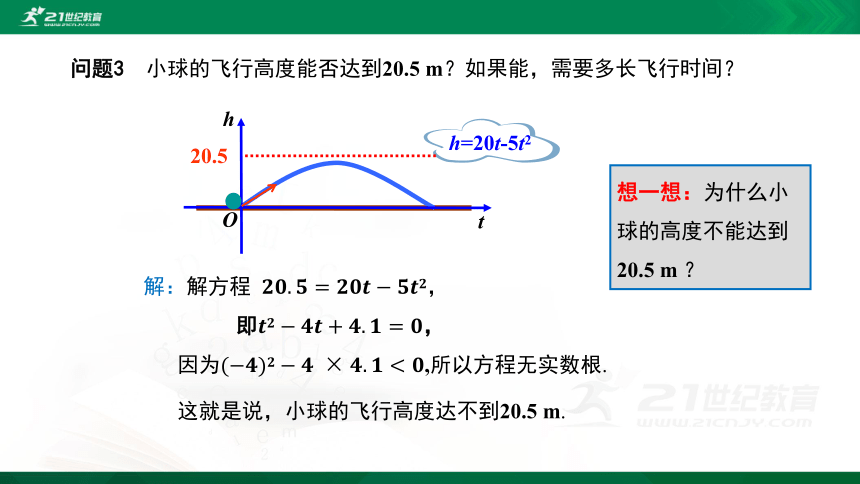
问题3 小球的飞行高度能否达到20.5 m?如果能,需要多长飞行时间?
O
h
t
20.5
因为(?????)??????????×????.?????
解:解方程 ????????.????=?????????????????????????,
即?????????????????+????.????=????,
?
h=20t-5t2
想一想:为什么小球的高度不能达到20.5 m ?
这就是说,小球的飞行高度达不到20.5 m.
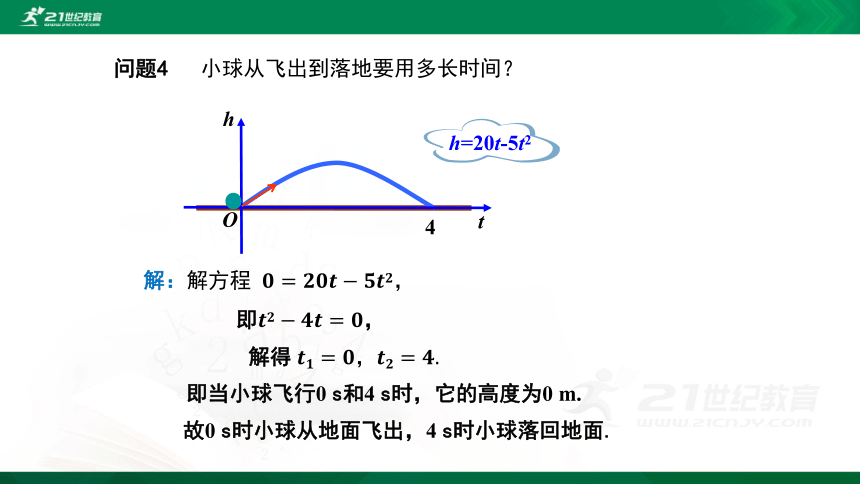
问题4 小球从飞出到落地要用多长时间?
O
h
t
4
解得 ????????=????,????????=????.
?
解:解方程 ????=?????????????????????????,
即?????????????????=????,
?
h=20t-5t2
即当小球飞行0 s和4 s时,它的高度为0 m.
故0 s时小球从地面飞出,4 s时小球落回地面.
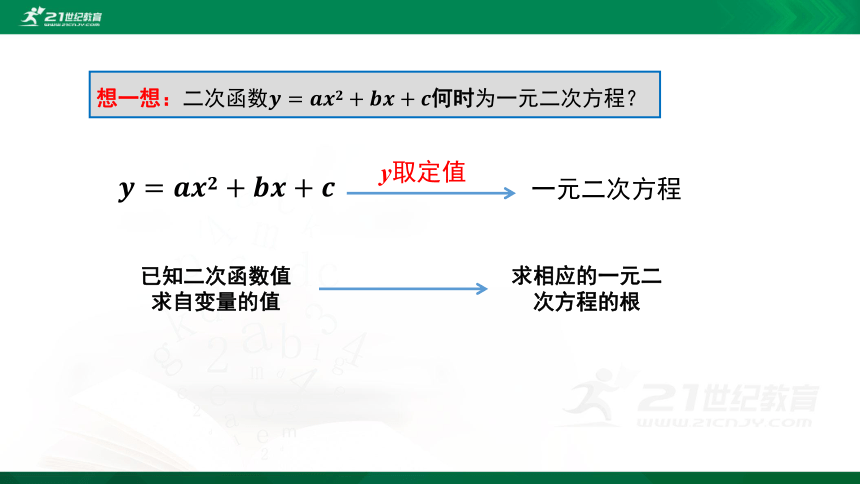
想一想:二次函数????=????????????+????????+????何时为一元二次方程?
?
????=????????????+????????+????
?
一元二次方程
y取定值
已知二次函数值求自变量的值
求相应的一元二次方程的根
2. 深入讨论二次函数与一元二次方程的关系
思考
下列二次函数的图象与x轴有公共点吗?如果有,公共点的横坐标是多少?当x取公共点的横坐标时,函数值是多少?由此,你能得出相应的一元二次方程的根吗?
(1)????=????????+?????????;
(2)????=?????????????????+????;
(3)????=?????????????+????.
?
观察图象,完成下表
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
抛物线与x轴公共点个数
公共点
横坐标
相应的一元二次
方程的根
0个
1个
2个
?????????????+????=????
无解
?
3
?????????????????+????=????,
????????=????????=????
?
?????,?????
?
????????+?????????=????,
????????=?????,????????=????
?
1
O
?????=?????????-????????+????
?
?????=?????????-????+????
?
?????=?????????+????-????
?
????
?
????
?
有两个交点
有两个不相等的实数根????????,????=?????±?????????????????????????????
?
??????????????????????>?????
?
有一个交点
有两个相等的实数根????????,????=?????????????
?
??????????????????????=?????
?
没有交点
没有实数根
???????????????????????
二次函数????=????????????+????????+????的图象与????轴交点的情况与对应的一元二次方程????????????+????????+????=????的根的情况
?
3.图象法解一元二次方程
利用函数图象求方程??????????????????????=????的实数根(结果保留小数点后一位).
?
例
解:画出函数????=??????????????????????的图象,
?
如图所示,
它与x轴的交点的横坐标大约是????.????,????.????.
?
所以方程??????????????????????=????的实数根为????????≈?????.????,????????≈????.????.
?
?????=???????????????????????
?
-2
2
2
4
6
4
-4
8
-2
-4
O
????
?
x
我们可以利用二次函数的图象求一元二次方程的根,由于作图或观察可能存在误差,由图象求得的根,一般是近似的.
4.二次函数与一元二次不等式的关系
抛物线????=????????????+????????+????
?
一元二次方程不等式????????????+????????+????>????
?
1
O
????
?
????
?
????=????????????+????????+????
?
抛物线????=????????????+????????+????在????轴上方的点所对应的????的值就是不等式????????????+????????+????>????的解集
?
二次函数????=????????????+????????+????与一元二次不等式????????????+????????+????>????及????????????+????????+?????
有两个交点????????,????????????,????
?
有一个交点????????,????
?
无交点
有两个交点????????,????????????,????
?
有一个交点????????,????
?
无交点
????????????
?
????≠????????
?
全体实数
?????????
无解
无解
?????????
无解
无解
????????????
?
????≠????????
?
全体实数
1
O
????
?
????
?
1
O
????
?
????
?
二次函数与一元二次方程
二次函数与一元二次方程的关系
二次函数????=????????????+????????+????与????轴的交点
?
一元二次方程????????????+????????+????=0的根的个数
?
有两个交点
课堂小结
根据函数图象求一元二次方程的近似解
如果抛物线????=????????????+????????+????与????轴的交点为????????,????????????,????,那么????????,????????即为方程????????????+????????+????=0的两个根
?
??????????????????????>?????
?
??????????????????????=?????
?
???????????????????????
一个交点
无交点
有两个不相等的实数根
有两个相等的实数根
无实数根
随堂训练
根据表格可得方程 ????????????+????????+?????=???? (????≠????,????、????、????为常数)一个解x的取值范围是( )
A. 6< x < 6.17 B. 6.17 < x < 6.18
C. 6.18?
x
6.17
6.18
6.19
6.20
0.02
0.06
C
1. 下列表格是二次函数????=????????????+????????+????的自变量????与函数值????的部分对应值:
?
3.若二次函数????=?????????+????????+????的部分图象如图所示,且关于x的一元二次方程?????????+????????+????=????的一个解????????=????,则另一个解????????= .
?
y
O
x
1
3
2.若二次函数????=??????????????????????+4的图象与????轴有且只有一个交点,则????的值为(?????????)
?
A. 1或????? B. 5或?????
C. ?5或???? D. 以上都不对
?
B
?????
?
4.已知二次函数????=?????????????????+????的图象如图所示,利用图象
回答问题:
(1)方程?????????????????+????=????的解是什么?
(2)x取什么值时,????>???? ?
(3)x取什么值时,?????
x
y
O
2
4
8
解:(1)????????=????,????????=????;
?
(2)????????;
?
(3)?????
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
22.2 二次函数与一元二次方程
2020年秋人教版数学九年级上册精品课件
学 习 目 标
3
1
2
了解用图象法求一元二次方程的近似根.
通过探索,理解二次函数与一元二次方程之间的联系.
能运用二次函数的图象与性质确定方程的解.
情景导入
问题:如图,以 40 m /s的速度将小球沿与地面成 30°角的方向击出时,小球的飞行路线是一条抛物线.如果不考虑空气阻力,小球的飞行高度h(单位:m)与飞行时间 ???? (单位:s)之间具有函数关系:h=?20??????–?5?????2???.
?
知识讲解
问题1 小球的飞行高度能否达到15 m?如果能,需要多长飞行时间?
1.二次函数与一元二次方程的关系
O
h
t
15
1
3
故当小球飞行1 s或3 s时,它的高度为15 m.
解:解方程 ????????=?????????????????????????,
即?????????????????+????=????,
解得 ????????=????,????????=????.
?
h=20t-5t2
想一想:为什么在这两个时间小球的高度为15m?
问题2 小球的飞行高度能否达到20 m?如果能,需要多长飞行时间?
O
h
t
20
2
故当小球飞行2 s时,它的高度为20 m.
解:解方程 ????????=?????????????????????????,
即?????????????????+????=????,
解得 ????????=????????=2.
?
h=20t-5t2
想一想:为什么只在一个时间小球的高度为20 m ?
问题3 小球的飞行高度能否达到20.5 m?如果能,需要多长飞行时间?
O
h
t
20.5
因为(?????)??????????×????.?????
解:解方程 ????????.????=?????????????????????????,
即?????????????????+????.????=????,
?
h=20t-5t2
想一想:为什么小球的高度不能达到20.5 m ?
这就是说,小球的飞行高度达不到20.5 m.
问题4 小球从飞出到落地要用多长时间?
O
h
t
4
解得 ????????=????,????????=????.
?
解:解方程 ????=?????????????????????????,
即?????????????????=????,
?
h=20t-5t2
即当小球飞行0 s和4 s时,它的高度为0 m.
故0 s时小球从地面飞出,4 s时小球落回地面.
想一想:二次函数????=????????????+????????+????何时为一元二次方程?
?
????=????????????+????????+????
?
一元二次方程
y取定值
已知二次函数值求自变量的值
求相应的一元二次方程的根
2. 深入讨论二次函数与一元二次方程的关系
思考
下列二次函数的图象与x轴有公共点吗?如果有,公共点的横坐标是多少?当x取公共点的横坐标时,函数值是多少?由此,你能得出相应的一元二次方程的根吗?
(1)????=????????+?????????;
(2)????=?????????????????+????;
(3)????=?????????????+????.
?
观察图象,完成下表
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
抛物线与x轴公共点个数
公共点
横坐标
相应的一元二次
方程的根
0个
1个
2个
?????????????+????=????
无解
?
3
?????????????????+????=????,
????????=????????=????
?
?????,?????
?
????????+?????????=????,
????????=?????,????????=????
?
1
O
?????=?????????-????????+????
?
?????=?????????-????+????
?
?????=?????????+????-????
?
????
?
????
?
有两个交点
有两个不相等的实数根????????,????=?????±?????????????????????????????
?
??????????????????????>?????
?
有一个交点
有两个相等的实数根????????,????=?????????????
?
??????????????????????=?????
?
没有交点
没有实数根
???????????????????????
二次函数????=????????????+????????+????的图象与????轴交点的情况与对应的一元二次方程????????????+????????+????=????的根的情况
?
3.图象法解一元二次方程
利用函数图象求方程??????????????????????=????的实数根(结果保留小数点后一位).
?
例
解:画出函数????=??????????????????????的图象,
?
如图所示,
它与x轴的交点的横坐标大约是????.????,????.????.
?
所以方程??????????????????????=????的实数根为????????≈?????.????,????????≈????.????.
?
?????=???????????????????????
?
-2
2
2
4
6
4
-4
8
-2
-4
O
????
?
x
我们可以利用二次函数的图象求一元二次方程的根,由于作图或观察可能存在误差,由图象求得的根,一般是近似的.
4.二次函数与一元二次不等式的关系
抛物线????=????????????+????????+????
?
一元二次方程不等式????????????+????????+????>????
?
1
O
????
?
????
?
????=????????????+????????+????
?
抛物线????=????????????+????????+????在????轴上方的点所对应的????的值就是不等式????????????+????????+????>????的解集
?
二次函数????=????????????+????????+????与一元二次不等式????????????+????????+????>????及????????????+????????+?????
有两个交点????????,????????????,????
?
有一个交点????????,????
?
无交点
有两个交点????????,????????????,????
?
有一个交点????????,????
?
无交点
????????????
?
????≠????????
?
全体实数
?????????
无解
无解
?????????
无解
无解
????????????
?
????≠????????
?
全体实数
1
O
????
?
????
?
1
O
????
?
????
?
二次函数与一元二次方程
二次函数与一元二次方程的关系
二次函数????=????????????+????????+????与????轴的交点
?
一元二次方程????????????+????????+????=0的根的个数
?
有两个交点
课堂小结
根据函数图象求一元二次方程的近似解
如果抛物线????=????????????+????????+????与????轴的交点为????????,????????????,????,那么????????,????????即为方程????????????+????????+????=0的两个根
?
??????????????????????>?????
?
??????????????????????=?????
?
???????????????????????
一个交点
无交点
有两个不相等的实数根
有两个相等的实数根
无实数根
随堂训练
根据表格可得方程 ????????????+????????+?????=???? (????≠????,????、????、????为常数)一个解x的取值范围是( )
A. 6< x < 6.17 B. 6.17 < x < 6.18
C. 6.18
x
6.17
6.18
6.19
6.20
0.02
0.06
C
1. 下列表格是二次函数????=????????????+????????+????的自变量????与函数值????的部分对应值:
?
3.若二次函数????=?????????+????????+????的部分图象如图所示,且关于x的一元二次方程?????????+????????+????=????的一个解????????=????,则另一个解????????= .
?
y
O
x
1
3
2.若二次函数????=??????????????????????+4的图象与????轴有且只有一个交点,则????的值为(?????????)
?
A. 1或????? B. 5或?????
C. ?5或???? D. 以上都不对
?
B
?????
?
4.已知二次函数????=?????????????????+????的图象如图所示,利用图象
回答问题:
(1)方程?????????????????+????=????的解是什么?
(2)x取什么值时,????>???? ?
(3)x取什么值时,?????
x
y
O
2
4
8
解:(1)????????=????,????????=????;
?
(2)????????;
?
(3)?????
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
同课章节目录
