22.3 .1 几何图形的最大面积问题课件(16张PPT)
文档属性
| 名称 | 22.3 .1 几何图形的最大面积问题课件(16张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-24 12:47:59 | ||
图片预览






文档简介
第二十二章 二次函数
22.3 实际问题与二次函数
第1课时 几何图形的最大面积问题
2020年秋人教版数学九年级上册精品课件
学 习 目 标
3
1
2
能应用二次函数的性质解决图形中的最大面积问题.
能够从实际问题中抽象出二次函数关系.
会运用二次函数知识求实际问题中的最大值或最小值,解决实际问题.
温故知新
写出下列抛物线的开口方向、对称轴和顶点坐标,并写出其最值.
(1)????=??????????????????????;(公式法)
(2)????=??????????????????+????.(配方法)
?
解:(1)开口方向:向上;对称轴:直线????=????;
顶点坐标: (????,?????);最小值:?????;
?
(2)开口方向:向下;对称轴:直线????=?????????;
顶点坐标: ?????????,????????????;最大值:???????????? .
?
知识讲解
二次函数解决几何图形面积的最值问题
用总长为60m的篱笆围成矩形场地,矩形面积S随矩形一边长l的变化而变化.当l是多少米时,场地的面积S最大?
例1
思考1 矩形面积公式是什么?
思考2 如何用l表示另一边?
思考3 面积S的函数关系式是什么?
矩形面积=长×宽
?
?????????????
?
????=????(?????????????)
?
解:矩形场地的周长是60 m,一边长为???? m,所以另一边长
为602?????? m. 场地的面积
?
????=????(30?????),
?
即 ????=?????2+30????(0?
因此,当????=?????????????=?????????????×?????=????????时,
?
也就是说,当????是15 m时,场地的面积????最大.
?
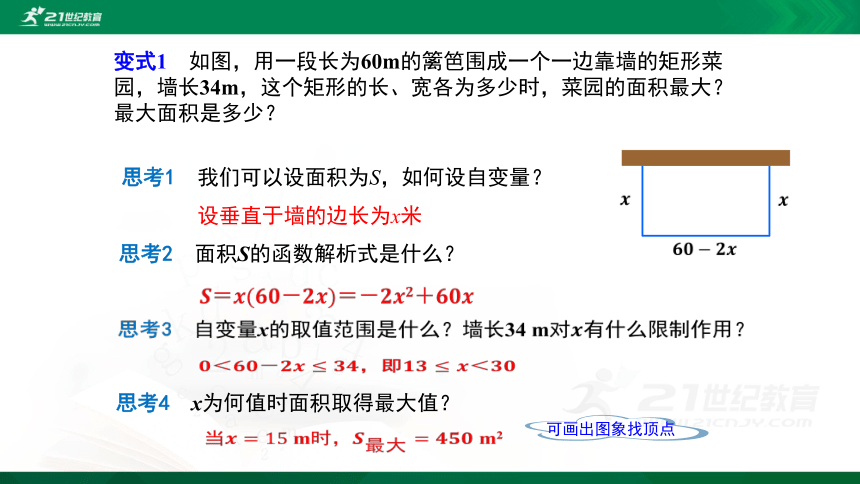
变式1 如图,用一段长为60m的篱笆围成一个一边靠墙的矩形菜园,墙长34m,这个矩形的长、宽各为多少时,菜园的面积最大?最大面积是多少?
????
?
????
?
?????????????????
?
思考1 我们可以设面积为S,如何设自变量?
设垂直于墙的边长为x米
思考2 面积S的函数解析式是什么?
????=????(????????-????????)=-????????????+????????????
?
思考3 自变量x的取值范围是什么?墙长34 m对????有什么限制作用?
?
????<????????-????????≤????????,即????????≤????<????????
?
思考4 x为何值时面积取得最大值?
当????=15 m时,????最大=???????????? m2
?
可画出图象找顶点
变式2 如图,用一段长为60m的篱笆围成一个一边靠墙的矩形菜园,墙长22 m,这个矩形的长、宽各为多少时,菜园的面积最大,最大面积是多少?
????
?
思考1 仿照变式1设未知数、列函数解析式.
设垂直于墙的边长为x m,则
思考2 若设与墙平行的一边为x m,则另一边如何表示?
?????=????(????????-????????)=-????????????+????????????.
?
????=??????????????????????=?????????????????+?????????????.
?
设矩形面积为S m2,与墙平行的一边为x m,则
?????????????????
?
思考3 当x=30时,S是否取得最大值?
思考4 自变量????的取值范围是什么?
?
????=??????????????????????????+????????????
?
不是
?????<??????≤????????
?
思考5 如何确定????的最大值?
?
由于?????????>????????,因此需要利用函数的增减性求其最值.当????=????????时,????有最大值418.
?
想一想:求面积最值时,变式1与变式2有何不同?
注意
实际问题中求解二次函数最值问题时,函数的最值要考虑自变量的取值范围:
(1)当自变量的取值包含顶点时,函数的最值在函数的顶点处取得;
(2)当自变量的取值不包含顶点时,函数的最值一般在端点处取得,此时要考虑函数的增减性.
如图所示的窗户边框的上部分是由4个全等扇形组成的半圆,下部分是矩形,现在制作一个窗户边框的材料总长度为6?m.(π取3)
(1)若设扇形半径为????,请用含????的代数式表示出????????的长,并求出????的取值范围.
(2)当????为何值时,窗户透光面积最大,最大面积为多少?(窗框厚度不予考虑)
?
例2
解:
(1)根据题意得,????????????+????????+????????≈????????????+????????????=????,
?
整理得,????????=?????????????;
?
根据?????????????>????,
?
得????的取值范围是:?????
?????设面积为????,则????=?????????????????????+????????????????=?????????????????????+????????=??????????????????????????????????+????????????????,
?
当????=????????????时,????最大=????????????????.
?
几何图形最大面积问题
解题关键
函数????=????????????+????????+????的顶点?????????????,?????????????????????????????
?
课堂小结
注意
依据常见几何图形的面积公式建立函数关系式
最值有时不在顶点处,此时要利用函数的增减性来确定
随堂训练
A. 6厘米 B. 12厘米 C. 24厘米 D. 36厘米
某种正方形合金板材的成本????(元)与它的面积成正比,设边长为????厘米,当????=????时,????=????????,那么当成本为????????元时,边长为( )
?
A
2.如图所示,在△????????????中,∠????=?????????°,????????=????????????????, ????????????=????????????????,动点P从点A开始沿AB向B以2 cm/s的速
度移动(不与点B重合),动点Q从点B开始沿 BC以
4cm/s的速度移动(不与点C重合).如果P、Q分别从A、
B同时出发,那么经过 秒,四边形APQC的面积
最小.
?
A
B
C
P
Q
3
3. 某广告公司设计一幅周长为16 m的矩形广告牌,广告设计费用每平方米1 000元,设矩形的一边长为x(m),面积为S(m2).
(1)写出S与x之间的解析式,并写出自变量x的取值范围;
(2)请你设计一个方案,使获得的设计费最多,并求出这个费用.
解: (1)设矩形一边长为x,则另一边长为(?????????).
?
根据题意,得????=????8?????=?????2+????????,其中0<????<8.
?
(????)????=?????????+????????=?(?????????)????+16,
?
∴当????=4时,即矩形的一边长为4 m时,矩形面积最大,为16 m2.
?
这时设计费最多,为16×1 000=1 6000(元).
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
22.3 实际问题与二次函数
第1课时 几何图形的最大面积问题
2020年秋人教版数学九年级上册精品课件
学 习 目 标
3
1
2
能应用二次函数的性质解决图形中的最大面积问题.
能够从实际问题中抽象出二次函数关系.
会运用二次函数知识求实际问题中的最大值或最小值,解决实际问题.
温故知新
写出下列抛物线的开口方向、对称轴和顶点坐标,并写出其最值.
(1)????=??????????????????????;(公式法)
(2)????=??????????????????+????.(配方法)
?
解:(1)开口方向:向上;对称轴:直线????=????;
顶点坐标: (????,?????);最小值:?????;
?
(2)开口方向:向下;对称轴:直线????=?????????;
顶点坐标: ?????????,????????????;最大值:???????????? .
?
知识讲解
二次函数解决几何图形面积的最值问题
用总长为60m的篱笆围成矩形场地,矩形面积S随矩形一边长l的变化而变化.当l是多少米时,场地的面积S最大?
例1
思考1 矩形面积公式是什么?
思考2 如何用l表示另一边?
思考3 面积S的函数关系式是什么?
矩形面积=长×宽
?
?????????????
?
????=????(?????????????)
?
解:矩形场地的周长是60 m,一边长为???? m,所以另一边长
为602?????? m. 场地的面积
?
????=????(30?????),
?
即 ????=?????2+30????(0?
因此,当????=?????????????=?????????????×?????=????????时,
?
也就是说,当????是15 m时,场地的面积????最大.
?
变式1 如图,用一段长为60m的篱笆围成一个一边靠墙的矩形菜园,墙长34m,这个矩形的长、宽各为多少时,菜园的面积最大?最大面积是多少?
????
?
????
?
?????????????????
?
思考1 我们可以设面积为S,如何设自变量?
设垂直于墙的边长为x米
思考2 面积S的函数解析式是什么?
????=????(????????-????????)=-????????????+????????????
?
思考3 自变量x的取值范围是什么?墙长34 m对????有什么限制作用?
?
????<????????-????????≤????????,即????????≤????<????????
?
思考4 x为何值时面积取得最大值?
当????=15 m时,????最大=???????????? m2
?
可画出图象找顶点
变式2 如图,用一段长为60m的篱笆围成一个一边靠墙的矩形菜园,墙长22 m,这个矩形的长、宽各为多少时,菜园的面积最大,最大面积是多少?
????
?
思考1 仿照变式1设未知数、列函数解析式.
设垂直于墙的边长为x m,则
思考2 若设与墙平行的一边为x m,则另一边如何表示?
?????=????(????????-????????)=-????????????+????????????.
?
????=??????????????????????=?????????????????+?????????????.
?
设矩形面积为S m2,与墙平行的一边为x m,则
?????????????????
?
思考3 当x=30时,S是否取得最大值?
思考4 自变量????的取值范围是什么?
?
????=??????????????????????????+????????????
?
不是
?????<??????≤????????
?
思考5 如何确定????的最大值?
?
由于?????????>????????,因此需要利用函数的增减性求其最值.当????=????????时,????有最大值418.
?
想一想:求面积最值时,变式1与变式2有何不同?
注意
实际问题中求解二次函数最值问题时,函数的最值要考虑自变量的取值范围:
(1)当自变量的取值包含顶点时,函数的最值在函数的顶点处取得;
(2)当自变量的取值不包含顶点时,函数的最值一般在端点处取得,此时要考虑函数的增减性.
如图所示的窗户边框的上部分是由4个全等扇形组成的半圆,下部分是矩形,现在制作一个窗户边框的材料总长度为6?m.(π取3)
(1)若设扇形半径为????,请用含????的代数式表示出????????的长,并求出????的取值范围.
(2)当????为何值时,窗户透光面积最大,最大面积为多少?(窗框厚度不予考虑)
?
例2
解:
(1)根据题意得,????????????+????????+????????≈????????????+????????????=????,
?
整理得,????????=?????????????;
?
根据?????????????>????,
?
得????的取值范围是:?????
?????设面积为????,则????=?????????????????????+????????????????=?????????????????????+????????=??????????????????????????????????+????????????????,
?
当????=????????????时,????最大=????????????????.
?
几何图形最大面积问题
解题关键
函数????=????????????+????????+????的顶点?????????????,?????????????????????????????
?
课堂小结
注意
依据常见几何图形的面积公式建立函数关系式
最值有时不在顶点处,此时要利用函数的增减性来确定
随堂训练
A. 6厘米 B. 12厘米 C. 24厘米 D. 36厘米
某种正方形合金板材的成本????(元)与它的面积成正比,设边长为????厘米,当????=????时,????=????????,那么当成本为????????元时,边长为( )
?
A
2.如图所示,在△????????????中,∠????=?????????°,????????=????????????????, ????????????=????????????????,动点P从点A开始沿AB向B以2 cm/s的速
度移动(不与点B重合),动点Q从点B开始沿 BC以
4cm/s的速度移动(不与点C重合).如果P、Q分别从A、
B同时出发,那么经过 秒,四边形APQC的面积
最小.
?
A
B
C
P
Q
3
3. 某广告公司设计一幅周长为16 m的矩形广告牌,广告设计费用每平方米1 000元,设矩形的一边长为x(m),面积为S(m2).
(1)写出S与x之间的解析式,并写出自变量x的取值范围;
(2)请你设计一个方案,使获得的设计费最多,并求出这个费用.
解: (1)设矩形一边长为x,则另一边长为(?????????).
?
根据题意,得????=????8?????=?????2+????????,其中0<????<8.
?
(????)????=?????????+????????=?(?????????)????+16,
?
∴当????=4时,即矩形的一边长为4 m时,矩形面积最大,为16 m2.
?
这时设计费最多,为16×1 000=1 6000(元).
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
同课章节目录
