23.1.2 旋转作图课件(20张PPT)
文档属性
| 名称 | 23.1.2 旋转作图课件(20张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-24 12:55:31 | ||
图片预览





文档简介
第二十三章 旋 转
23.1 图形的旋转
第2课时旋转作图
2020年秋人教版数学九年级上册精品课件
学习目标
1
2
会按照要求作出旋转后的图形.(重点)
了解旋转角和旋转中心的改变可以得到不同效果的美丽的图案,体验旋转在现实生活中的应用.
知识讲解
1.图形旋转的基本性质
(2)对应点到旋转中心的距离相等;
(4)旋转不改变图形的大小和形状;
(5)旋转中心是唯一不动的点.
(3)对应线段相等,对应角相等;
(1)各组对应点与旋转中心的连线所成的角相等,都等于旋转角;
2. 旋转作图的步骤
(1)定:确定原图形中每一个关键点与旋转中心;
(2)连:连接图形中每一个关键点与旋转中心;
(3)转:把连线按要求绕旋转中心转过一定角度(作旋转角);
(4)截:在角的另一边上截取与关键点到旋转中心的距离相等的线段,得到各点的对应点;
(5)连:连接所得到的各对应点;
(6)写:写出结论,说明作出的图形.
如图,画出线段 AB绕点A按顺时针方向旋转60°后的线段.
作法:(1)如图,以AB为一边按顺时针方向画∠BAX,使得∠BAX=60°;
(2)在射线AX上取点C,使得AC=AB,线段AC即为所求.
X
C
一、简单的旋转作图
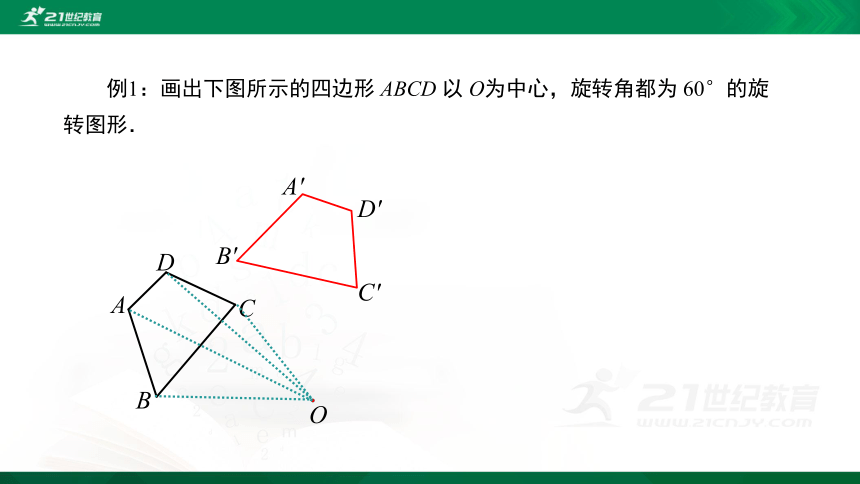
例1:画出下图所示的四边形 ABCD 以 O为中心,旋转角都为 60°的旋转图形.
A
B
C
D
O
B'
A'
C'
D'
A
B
E′
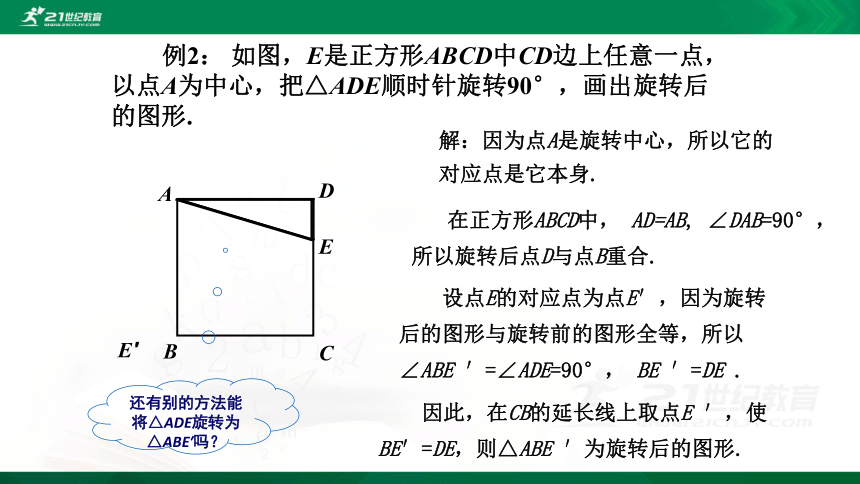
还有别的方法能将△ADE旋转为△ABE′吗?
例2: 如图,E是正方形ABCD中CD边上任意一点,以点A为中心,把△ADE顺时针旋转90°,画出旋转后的图形.
C
D
E
设点E的对应点为点E′,因为旋转后的图形与旋转前的图形全等,所以∠ABE ′=∠ADE=90°, BE ′=DE .
解:因为点A是旋转中心,所以它的对应点是它本身.
在正方形ABCD中, AD=AB, ∠DAB=90°,所以旋转后点D与点B重合.
因此,在CB的延长线上取点E ′,使BE′=DE,则△ABE ′为旋转后的图形.
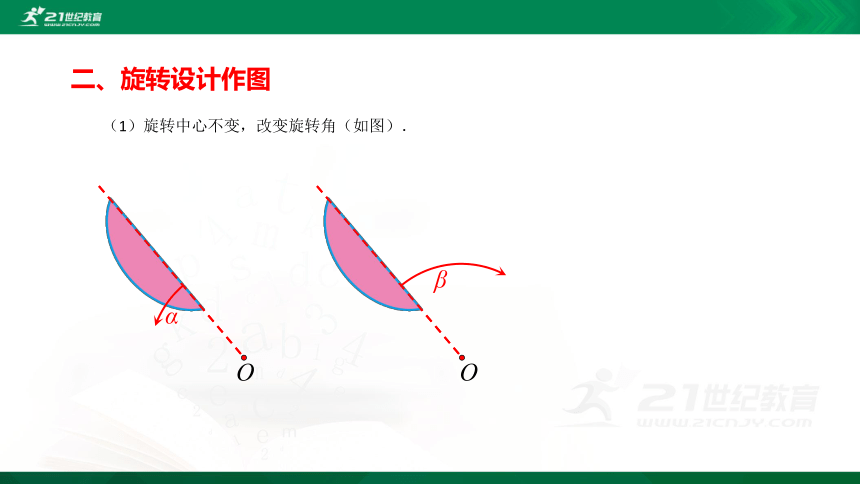
二、旋转设计作图
(1)旋转中心不变,改变旋转角(如图).
O
O
β
α
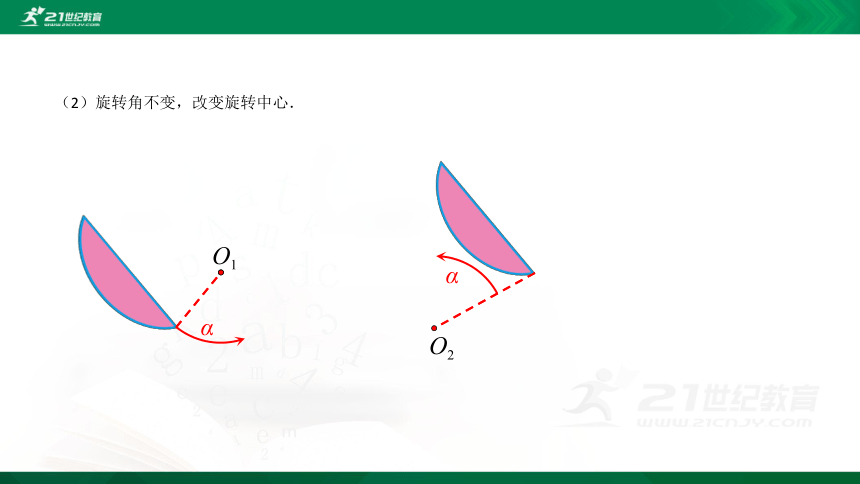
O1
α
O2
α
(2)旋转角不变,改变旋转中心.
(3)设计美丽的图案.
O
例1 如下图是某一种花的花瓣和中心,现以 O 为旋转中心画出分别旋转 45°, 90° ,135° ,180° , 225°, 270°, 315°的这种花的图形.
随堂训练
1.如图,在正方形网格中,将△ABC绕点A旋转后得到△ADE,则下列旋转方式中,符合题意的是( )
A.顺时针旋转90° B.逆时针旋转90°
C.顺时针旋转45° D.逆时针旋转45°
B
随堂训练
2.如图,它可以看作是由一个菱形绕某一点旋转一个角度后,顺次按这个角度同向旋转而得到的,
①请你在图中用字母O标注出这一点;
②每次旋转了_______度;
③一共旋转了_______次.
O
60
5
随堂训练
3. 如图,△ABC 的顶点坐标
分别为A(4,6)、B(5,2)、
C(2,1),如果将△ABC
绕点C按逆时针方向旋转
90°,得到△ ,那么点A′
的对应点的坐标是( )
A.(-3,3) B.(3,-3) C.(-2,4) D.(1,4)
7
O
-2
-4
-3
-5
y
C
-1
6
A
2
1
3
4
5
1
2
B
x
3
4
5
A
4.画出下图所示的四边形 ABCD 以 O 点为中心,旋转角分别为 30°,60°的旋转图形.
O
A
B
C
D
A
B
C
D
O
A′
B′
C′
D′
O
A
B
C
D
A′
D′
C′
B′
顺时针旋转 60°
顺时针旋转 30°
课堂小结
旋转
作图
作旋转图形
作图基本步骤五步
设计图案
改变旋转中心
改变旋转角
1.定
2.连
3.转
4.截
5.连
6.写
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
23.1 图形的旋转
第2课时旋转作图
2020年秋人教版数学九年级上册精品课件
学习目标
1
2
会按照要求作出旋转后的图形.(重点)
了解旋转角和旋转中心的改变可以得到不同效果的美丽的图案,体验旋转在现实生活中的应用.
知识讲解
1.图形旋转的基本性质
(2)对应点到旋转中心的距离相等;
(4)旋转不改变图形的大小和形状;
(5)旋转中心是唯一不动的点.
(3)对应线段相等,对应角相等;
(1)各组对应点与旋转中心的连线所成的角相等,都等于旋转角;
2. 旋转作图的步骤
(1)定:确定原图形中每一个关键点与旋转中心;
(2)连:连接图形中每一个关键点与旋转中心;
(3)转:把连线按要求绕旋转中心转过一定角度(作旋转角);
(4)截:在角的另一边上截取与关键点到旋转中心的距离相等的线段,得到各点的对应点;
(5)连:连接所得到的各对应点;
(6)写:写出结论,说明作出的图形.
如图,画出线段 AB绕点A按顺时针方向旋转60°后的线段.
作法:(1)如图,以AB为一边按顺时针方向画∠BAX,使得∠BAX=60°;
(2)在射线AX上取点C,使得AC=AB,线段AC即为所求.
X
C
一、简单的旋转作图
例1:画出下图所示的四边形 ABCD 以 O为中心,旋转角都为 60°的旋转图形.
A
B
C
D
O
B'
A'
C'
D'
A
B
E′
还有别的方法能将△ADE旋转为△ABE′吗?
例2: 如图,E是正方形ABCD中CD边上任意一点,以点A为中心,把△ADE顺时针旋转90°,画出旋转后的图形.
C
D
E
设点E的对应点为点E′,因为旋转后的图形与旋转前的图形全等,所以∠ABE ′=∠ADE=90°, BE ′=DE .
解:因为点A是旋转中心,所以它的对应点是它本身.
在正方形ABCD中, AD=AB, ∠DAB=90°,所以旋转后点D与点B重合.
因此,在CB的延长线上取点E ′,使BE′=DE,则△ABE ′为旋转后的图形.
二、旋转设计作图
(1)旋转中心不变,改变旋转角(如图).
O
O
β
α
O1
α
O2
α
(2)旋转角不变,改变旋转中心.
(3)设计美丽的图案.
O
例1 如下图是某一种花的花瓣和中心,现以 O 为旋转中心画出分别旋转 45°, 90° ,135° ,180° , 225°, 270°, 315°的这种花的图形.
随堂训练
1.如图,在正方形网格中,将△ABC绕点A旋转后得到△ADE,则下列旋转方式中,符合题意的是( )
A.顺时针旋转90° B.逆时针旋转90°
C.顺时针旋转45° D.逆时针旋转45°
B
随堂训练
2.如图,它可以看作是由一个菱形绕某一点旋转一个角度后,顺次按这个角度同向旋转而得到的,
①请你在图中用字母O标注出这一点;
②每次旋转了_______度;
③一共旋转了_______次.
O
60
5
随堂训练
3. 如图,△ABC 的顶点坐标
分别为A(4,6)、B(5,2)、
C(2,1),如果将△ABC
绕点C按逆时针方向旋转
90°,得到△ ,那么点A′
的对应点的坐标是( )
A.(-3,3) B.(3,-3) C.(-2,4) D.(1,4)
7
O
-2
-4
-3
-5
y
C
-1
6
A
2
1
3
4
5
1
2
B
x
3
4
5
A
4.画出下图所示的四边形 ABCD 以 O 点为中心,旋转角分别为 30°,60°的旋转图形.
O
A
B
C
D
A
B
C
D
O
A′
B′
C′
D′
O
A
B
C
D
A′
D′
C′
B′
顺时针旋转 60°
顺时针旋转 30°
课堂小结
旋转
作图
作旋转图形
作图基本步骤五步
设计图案
改变旋转中心
改变旋转角
1.定
2.连
3.转
4.截
5.连
6.写
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
同课章节目录
