23.1.1 旋转的概念与性质课件(24张PPT)
文档属性
| 名称 | 23.1.1 旋转的概念与性质课件(24张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-24 00:00:00 | ||
图片预览








文档简介
第二十三章 旋 转
23.1 图形的旋转
第1课时 旋转的概念与性质
2020年秋人教版数学九年级上册精品课件
学 习 目 标
1
2
了解旋转的概念,理解图形旋转的三要素“旋转中心、旋转方向和旋转角”.(重点)
理解旋转的性质,并会运用其解决简单的旋转问题.(重点)
游乐园里的摩天轮、旋转木马、海盗船的运动有什么共同点?
新课导入
你去过游乐园吗?
摩天轮
生活中转动的风扇扇叶,正在拧螺丝的扳手是不是也具有这种特点呢?
正在拧螺丝的扳手
转动的风扇扇叶
把时针当成一个图形,那么它可以绕着中心固定点转动一定角度.
钟表的指针在不停地转动,从12时到4时,时针转动了______度.
120
怎样来定义这种图形变换?
把叶片当成一个平面图形,那么它可以绕着平面内中心固定点转动一定角度.
风车风轮的每个叶片在风的吹动下转动到新的位置.
知识讲解
1. 旋转的概念
把一个图形绕着某一定点O 转动一定角度的图形变换叫做旋转.这个定点O 叫旋转中心,转动的角叫做旋转角.
.
如果图形上的点 P 经过旋转变为点 P′,那么这两个点叫做这个旋转的对应点.
O
P
120°
旋转中心、旋转方向、旋转角又称为旋转的三要素.
P?
例1.下列现象中属于旋转的有( )个.
①地下水位逐年下降;②传送带的移动;
③方向盘的转动; ④水龙头的转动;
⑤钟摆的运动; ⑥荡秋千.
A.2 B.3 C.4 D.5
C
例2.时钟的时针在不停地转动,从上午 6 时到上午 9 时,时针旋转的旋转角是多少度?从上午 9 时到上午 10 时呢?
解:从上午 6 时到上午 9 时,时针旋转的旋转角为90度,从上午 9 时到上午 10 时,时针旋转的旋转角为30度.
B?
A ?
B
A
C?
C
O
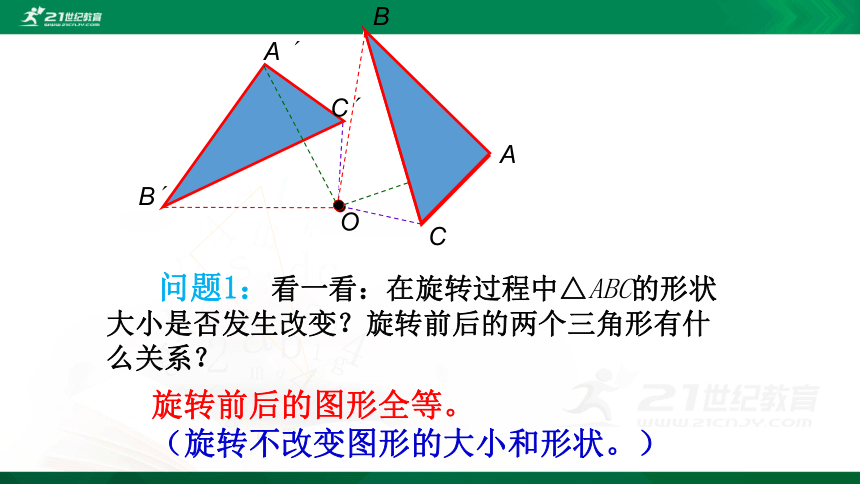
问题1:看一看:在旋转过程中△ABC的形状大小是否发生改变?旋转前后的两个三角形有什么关系?
旋转前后的图形全等。
(旋转不改变图形的大小和形状。)
B ?
A ?
B
A
C?
C
O
对应点到旋转中心的距离相等。
OA=OA ′ , OC=OC ′
OB=OB′
问题2:量一量:图中的OB和哪条线段相等?还有没有类似这样对应相等的线段呢?
B
A
B?
A?
C
C?
O
问题3:找一找:找出旋转的旋转角,这些角有什么关系?
对应点与旋转中心所连线段的夹角等于旋转角。
∠AOA ′ ∠BOB ′ ∠COC′
= =
旋转前后的图形全等;
(旋转不改变图形的大小和形状)
对应点到旋转中心的距离相等;
对应点与旋转中心所连线段的夹角等于旋转角.
旋转的性质:
例3. △A ′ OB ′是△AOB绕点O按逆时针方向旋转得到的.已知∠AOB=20 °, ∠ A ′ OB =24°,AB=3,OA=5,则A ′ B ′ = ,OA ′ = ,旋转角= .
3
5
44 °
知识讲解
例4.把一副三角板按如图①放置,其中∠ACB=∠DEC=90°,∠A=45°,∠D=30°,斜边AB=6 cm,DC=7 cm.把三角板DCE绕点C顺时针旋转15°得到△D1CE1(如图②).这时AB与CD1相交于点O、与D1E1相交于点F.
(1)求线段AD1的长;
(2)若把三角形D1CE1绕着点C顺时针再旋转30°得△D2CE2,这时点B在△D2CE2的内部、外部、还是边上?说明理由.
① ②
知识讲解
解:(1)∵ 旋转角为15°,∴ ∠OCB=60°﹣15°=45°,
∴ ∠COB=180°﹣45°﹣45°=90°,∴ CD1⊥AB,
∴ AO=CO=12 AB=12 ×6=3,∴ OD1=DC﹣CO=7﹣3=4,
在Rt△AD1O中,由勾股定理得,AD1=????????2+????????12=32+42=5 .
(2)点B在△D2CE2的内部.
理由如下:设直线CB与D2E2相交于点P,
∵ △D1CE1绕着点C顺时针再旋转30°,∴ ∠PCE2=15°+30°=45°,
∴ △CPE2是等腰直角三角形,∴ CP= CE2= 722?,
∵ AB=6,∴ CB= 22AB=3 2< 722 ,即CB<CP,
∴ 点B在△D2CE2的内部.
?
知识讲解
随堂训练
1.如图,如果正方形CDEF旋转后能与正方形ABCD重合,那么图形所在的平面上可以作为旋转中心的点共有______个.
3
A
B
F
E
C
D
A
B
C
D
E
2.如图,将Rt△ABC绕点A按顺时针方向旋转一定角度得Rt △ADE,点B的对应点D恰好落在BC边上.若AC= , ∠B=60 °,则CD的长为( )
A. 0.5 B. 1.5 C. D. 1
D
随堂训练
3.如图,正方形A′B′C′D′是由正方形ABCD按顺时针方向旋转45°而成的.
(1)若AB=4,则S正方形A′B′C′D′= ;
(2) ∠BAB ′= , ∠B′AD= .
(3)若连接BB′,则∠ABB′= .
16
45°
45°
67.5°
4.如图,在Rt△ABC中,∠ACB=90°,∠B=30°,AC=2,将△ABC绕点C逆时针旋转至△A′B′C,使得点A′恰好落在AB上,A′B′与BC交于点D,则△A′CD的面积为( )
A.1 B. 32 C. 3 D.2 3
?
B
5.如图,杠杆绕支点转动撬起重物,杠杆的旋转中心在哪里?旋转角是哪个角?
答案: O点 ∠AOA′或∠BOB′
课堂小结
旋转
定义
三要素:旋转中心,旋转方向和旋转角度
性质
(1)旋转前后的图形全等;
(2)对应点到旋转中心的距离相等;
(3)对应点与旋转中心所连线段的夹角等于旋转角
应用
确定旋转中心
两对对应点所连线段的垂直平分线的交点
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
23.1 图形的旋转
第1课时 旋转的概念与性质
2020年秋人教版数学九年级上册精品课件
学 习 目 标
1
2
了解旋转的概念,理解图形旋转的三要素“旋转中心、旋转方向和旋转角”.(重点)
理解旋转的性质,并会运用其解决简单的旋转问题.(重点)
游乐园里的摩天轮、旋转木马、海盗船的运动有什么共同点?
新课导入
你去过游乐园吗?
摩天轮
生活中转动的风扇扇叶,正在拧螺丝的扳手是不是也具有这种特点呢?
正在拧螺丝的扳手
转动的风扇扇叶
把时针当成一个图形,那么它可以绕着中心固定点转动一定角度.
钟表的指针在不停地转动,从12时到4时,时针转动了______度.
120
怎样来定义这种图形变换?
把叶片当成一个平面图形,那么它可以绕着平面内中心固定点转动一定角度.
风车风轮的每个叶片在风的吹动下转动到新的位置.
知识讲解
1. 旋转的概念
把一个图形绕着某一定点O 转动一定角度的图形变换叫做旋转.这个定点O 叫旋转中心,转动的角叫做旋转角.
.
如果图形上的点 P 经过旋转变为点 P′,那么这两个点叫做这个旋转的对应点.
O
P
120°
旋转中心、旋转方向、旋转角又称为旋转的三要素.
P?
例1.下列现象中属于旋转的有( )个.
①地下水位逐年下降;②传送带的移动;
③方向盘的转动; ④水龙头的转动;
⑤钟摆的运动; ⑥荡秋千.
A.2 B.3 C.4 D.5
C
例2.时钟的时针在不停地转动,从上午 6 时到上午 9 时,时针旋转的旋转角是多少度?从上午 9 时到上午 10 时呢?
解:从上午 6 时到上午 9 时,时针旋转的旋转角为90度,从上午 9 时到上午 10 时,时针旋转的旋转角为30度.
B?
A ?
B
A
C?
C
O
问题1:看一看:在旋转过程中△ABC的形状大小是否发生改变?旋转前后的两个三角形有什么关系?
旋转前后的图形全等。
(旋转不改变图形的大小和形状。)
B ?
A ?
B
A
C?
C
O
对应点到旋转中心的距离相等。
OA=OA ′ , OC=OC ′
OB=OB′
问题2:量一量:图中的OB和哪条线段相等?还有没有类似这样对应相等的线段呢?
B
A
B?
A?
C
C?
O
问题3:找一找:找出旋转的旋转角,这些角有什么关系?
对应点与旋转中心所连线段的夹角等于旋转角。
∠AOA ′ ∠BOB ′ ∠COC′
= =
旋转前后的图形全等;
(旋转不改变图形的大小和形状)
对应点到旋转中心的距离相等;
对应点与旋转中心所连线段的夹角等于旋转角.
旋转的性质:
例3. △A ′ OB ′是△AOB绕点O按逆时针方向旋转得到的.已知∠AOB=20 °, ∠ A ′ OB =24°,AB=3,OA=5,则A ′ B ′ = ,OA ′ = ,旋转角= .
3
5
44 °
知识讲解
例4.把一副三角板按如图①放置,其中∠ACB=∠DEC=90°,∠A=45°,∠D=30°,斜边AB=6 cm,DC=7 cm.把三角板DCE绕点C顺时针旋转15°得到△D1CE1(如图②).这时AB与CD1相交于点O、与D1E1相交于点F.
(1)求线段AD1的长;
(2)若把三角形D1CE1绕着点C顺时针再旋转30°得△D2CE2,这时点B在△D2CE2的内部、外部、还是边上?说明理由.
① ②
知识讲解
解:(1)∵ 旋转角为15°,∴ ∠OCB=60°﹣15°=45°,
∴ ∠COB=180°﹣45°﹣45°=90°,∴ CD1⊥AB,
∴ AO=CO=12 AB=12 ×6=3,∴ OD1=DC﹣CO=7﹣3=4,
在Rt△AD1O中,由勾股定理得,AD1=????????2+????????12=32+42=5 .
(2)点B在△D2CE2的内部.
理由如下:设直线CB与D2E2相交于点P,
∵ △D1CE1绕着点C顺时针再旋转30°,∴ ∠PCE2=15°+30°=45°,
∴ △CPE2是等腰直角三角形,∴ CP= CE2= 722?,
∵ AB=6,∴ CB= 22AB=3 2< 722 ,即CB<CP,
∴ 点B在△D2CE2的内部.
?
知识讲解
随堂训练
1.如图,如果正方形CDEF旋转后能与正方形ABCD重合,那么图形所在的平面上可以作为旋转中心的点共有______个.
3
A
B
F
E
C
D
A
B
C
D
E
2.如图,将Rt△ABC绕点A按顺时针方向旋转一定角度得Rt △ADE,点B的对应点D恰好落在BC边上.若AC= , ∠B=60 °,则CD的长为( )
A. 0.5 B. 1.5 C. D. 1
D
随堂训练
3.如图,正方形A′B′C′D′是由正方形ABCD按顺时针方向旋转45°而成的.
(1)若AB=4,则S正方形A′B′C′D′= ;
(2) ∠BAB ′= , ∠B′AD= .
(3)若连接BB′,则∠ABB′= .
16
45°
45°
67.5°
4.如图,在Rt△ABC中,∠ACB=90°,∠B=30°,AC=2,将△ABC绕点C逆时针旋转至△A′B′C,使得点A′恰好落在AB上,A′B′与BC交于点D,则△A′CD的面积为( )
A.1 B. 32 C. 3 D.2 3
?
B
5.如图,杠杆绕支点转动撬起重物,杠杆的旋转中心在哪里?旋转角是哪个角?
答案: O点 ∠AOA′或∠BOB′
课堂小结
旋转
定义
三要素:旋转中心,旋转方向和旋转角度
性质
(1)旋转前后的图形全等;
(2)对应点到旋转中心的距离相等;
(3)对应点与旋转中心所连线段的夹角等于旋转角
应用
确定旋转中心
两对对应点所连线段的垂直平分线的交点
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
同课章节目录
