24.2.1 点和圆的位置关系课件(21张PPT)
文档属性
| 名称 | 24.2.1 点和圆的位置关系课件(21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-24 13:11:25 | ||
图片预览




文档简介
第 二十四章 圆
24.2 点和圆、直线和圆的位置关系
24.2.1 点和圆的位置关系
2020年秋人教版数学九年级上册精品课件
学习目标
1.理解并掌握点和圆的三种位置关系.(重点)
2.理解不在同一直线上的三个点确定一个圆及其运用.(重点)
3.了解三角形的外接圆和三角形外心的概念.
4.了解反证法的证明思想.
问题: 观察下列图片.是一个小朋友玩飞镖游戏时在靶子上留下的小孔,这些小孔和这些同心圆是什么关系呢?
新课导入
点和圆的位置关系
1
知识讲解
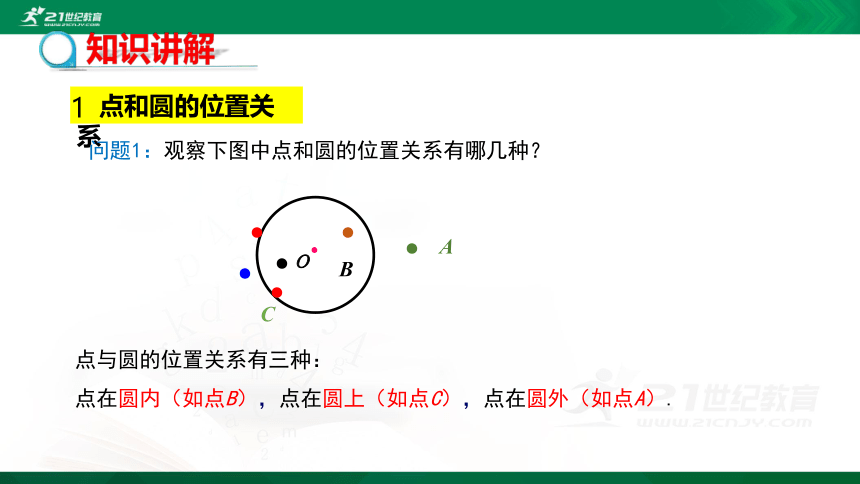
问题1:观察下图中点和圆的位置关系有哪几种?
.
o
.
C
.
.
. B
.A
.
点与圆的位置关系有三种:
点在圆内(如点B),点在圆上(如点C),点在圆外(如点A).
dd=r
d>r
问题2:如何用数量关系来表示点和圆的位置关系呢?
⑴点在圆内
·
P
⑵点在圆上
·
P
⑶点在圆外
·
P
d
d
d
注:“ ”读作“等价于”,它表示从符号的左边可以推出 ,从右边可以推出 .
右边
左边
·
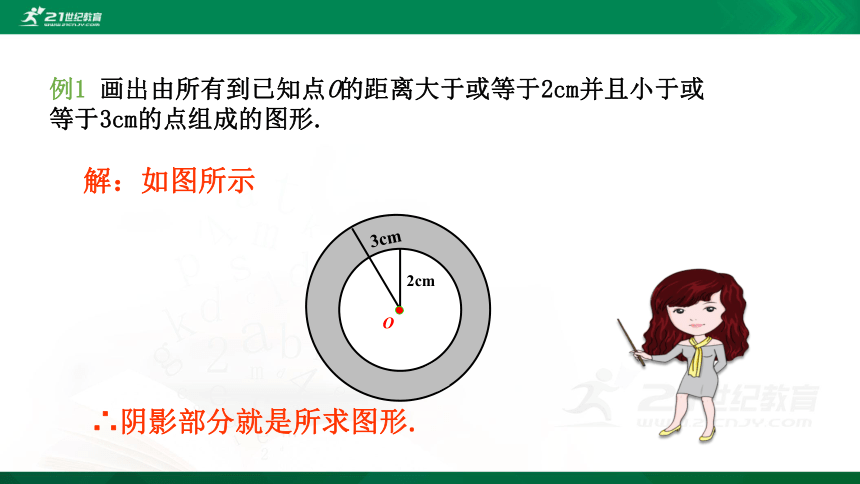
例1 画出由所有到已知点O的距离大于或等于2cm并且小于或等于3cm的点组成的图形.
·
O
2cm
3cm
解:如图所示
∴阴影部分就是所求图形.
过不在同一直线上的三个点作圆
2
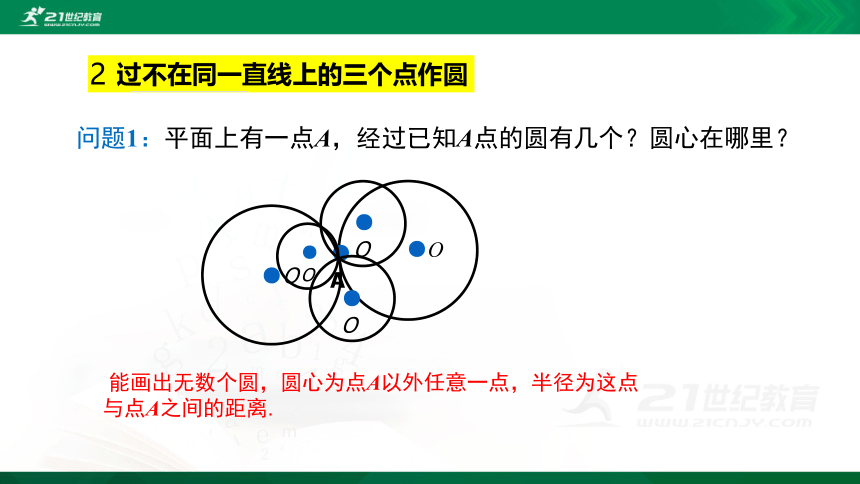
问题1:平面上有一点A,经过已知A点的圆有几个?圆心在哪里?
●O
●A
●O
●O
●O
●O
能画出无数个圆,圆心为点A以外任意一点,半径为这点与点A之间的距离.
r2
r1
·
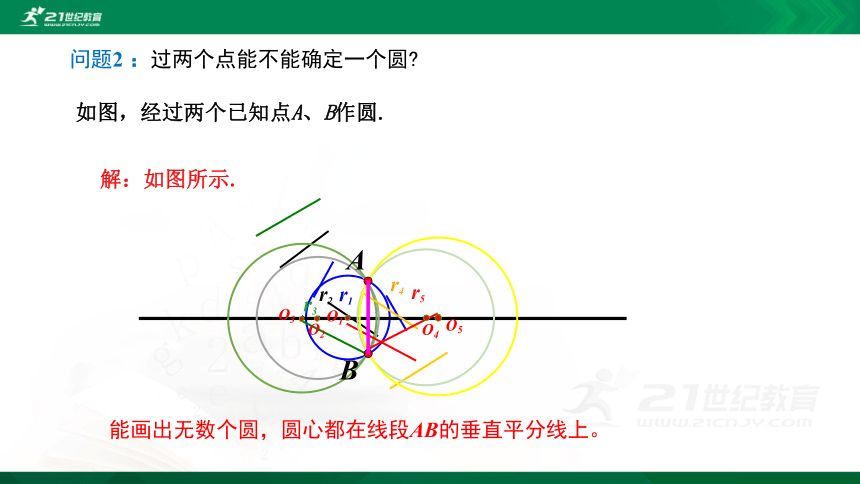
问题2 :过两个点能不能确定一个圆?
如图,经过两个已知点A、B作圆.
·
O2
O1
O3
·
·
O4
r4
O5
·
r5
B
A
解:如图所示.
能画出无数个圆,圆心都在线段AB的垂直平分线上。
r3
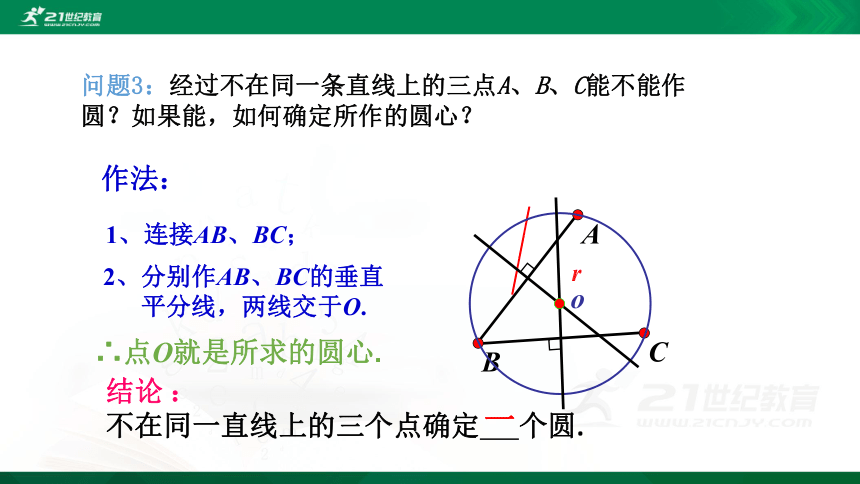
问题3:经过不在同一条直线上的三点A、B、C能不能作圆?如果能,如何确定所作的圆心?
∴点O就是所求的圆心.
作法:
1、连接AB、BC;
2、分别作AB、BC的垂直
平分线,两线交于O.
A
C
B
·
r
o
结论 :
不在同一直线上的三个点确定 个圆.
一
三角形的外心
3
(1)经过三角形(△ABC)的三个顶点可以作 圆,这个圆叫做三角形的 圆(⊙O) .
(2)外接圆的圆心是三角形三条边的 交点,叫做这个三角形的 .
一个
外接
垂直平分线
外心
到三角形三个顶点的距离相等.
●O
A
B
C
作图:
三角形三边中垂线的交点.
性质:
例2分别画一个锐角三角形、直角三角形和钝角三角形,再画出它们的外接圆,观察并叙述各三角形与它的外心的位置关系.
1.锐角三角形的外心位于三角形内,
2.直角三角形的外心位于直角三角形斜边的中点处,
3.钝角三角形的外心位于三角形外.
A
B
C
●O
A
B
C
C
A
B
┐
●O
●O
反证法
4
1.反证法:不是直接从命题的已知得出结论,而是假设命题的结论 ,由此经过推理得出矛盾,由矛盾断定所作假设不正确,从而得到命题成立.这种证明方法叫做 .
不成立
反证法
假设命题的结论不成立;
从这个假设出发,经过推理,得出矛盾;
由矛盾判定假设不正确,从而肯定命题的结论正确.
2.反证法的一般步骤:
例3 用反证法的证明:经过同一条直线上的点不能作出一个圆.
证明:如图假设过同一直线l上的A、B、C三点可以作一个圆,设这个圆的圆心为P,那么点P既在线段AB的垂直平分线l1,又在线段 的垂直平分线l2,即点P为L1与l2的 点,而l1⊥l,l2⊥l,这与我们以前所学的“过一点有且只
有 条直线与已知直线 ”矛盾.
所以,过同一直线上的三点不能作圆.
BC
交
一
垂直
l1
l2
A
B
C
P
新课讲解
随堂训练
1.⊙O的半径为10cm,A、B、C三点到圆心的距离分别为8cm、10cm、12cm,则点A、B、C与⊙O的位置关系是:
点A在 ;点B在 ;点C在 .
练一练:
圆内
圆上
圆外
2.圆心为O的两个同心圆,半径分别为1和2,若OP= ,则点P在( )
A.在大圆内 B.在小圆内
C.小圆外 D.大圆内、小圆外
o
D
3、体育课上,小王和小孙的铅球成绩分别是6.4m和5.1m,他们投入的铅球分别落在图中哪个区域内?
解:小王投入的铅球落在6-7m的区域内,小孙投入的铅球落在5-6m的区域内.
4.下列说法是否正确?
(1)任意的一个三角形一定有一个外接圆( )
(2)任意一个圆有且只有一个内接三角形( )
(3)经过三点一定可以确定一个圆( )
(4)三角形的外心到三角形各顶点的距离相等( )
√
×
×
√
5.如图,是一块圆形镜片破碎后的部分残片,试找出它的圆心.
A
B
C
O
圆心一定在弦的垂直平分线上.
课堂小结
点与圆的位置关系
点在圆外
点在圆上
点在圆内
d>r
d=r
d位置关系数量化
作圆
过一点可以作无数个圆
过两点可以作无数个圆
过不在同一直线上的三个点确定一个圆
直角三角形的外心在斜边中点处
注意:过同一直线上的三个点不能作圆
点P在圆环内
r≤d≤R
R
r
P
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
24.2 点和圆、直线和圆的位置关系
24.2.1 点和圆的位置关系
2020年秋人教版数学九年级上册精品课件
学习目标
1.理解并掌握点和圆的三种位置关系.(重点)
2.理解不在同一直线上的三个点确定一个圆及其运用.(重点)
3.了解三角形的外接圆和三角形外心的概念.
4.了解反证法的证明思想.
问题: 观察下列图片.是一个小朋友玩飞镖游戏时在靶子上留下的小孔,这些小孔和这些同心圆是什么关系呢?
新课导入
点和圆的位置关系
1
知识讲解
问题1:观察下图中点和圆的位置关系有哪几种?
.
o
.
C
.
.
. B
.A
.
点与圆的位置关系有三种:
点在圆内(如点B),点在圆上(如点C),点在圆外(如点A).
d
d>r
问题2:如何用数量关系来表示点和圆的位置关系呢?
⑴点在圆内
·
P
⑵点在圆上
·
P
⑶点在圆外
·
P
d
d
d
注:“ ”读作“等价于”,它表示从符号的左边可以推出 ,从右边可以推出 .
右边
左边
·
例1 画出由所有到已知点O的距离大于或等于2cm并且小于或等于3cm的点组成的图形.
·
O
2cm
3cm
解:如图所示
∴阴影部分就是所求图形.
过不在同一直线上的三个点作圆
2
问题1:平面上有一点A,经过已知A点的圆有几个?圆心在哪里?
●O
●A
●O
●O
●O
●O
能画出无数个圆,圆心为点A以外任意一点,半径为这点与点A之间的距离.
r2
r1
·
问题2 :过两个点能不能确定一个圆?
如图,经过两个已知点A、B作圆.
·
O2
O1
O3
·
·
O4
r4
O5
·
r5
B
A
解:如图所示.
能画出无数个圆,圆心都在线段AB的垂直平分线上。
r3
问题3:经过不在同一条直线上的三点A、B、C能不能作圆?如果能,如何确定所作的圆心?
∴点O就是所求的圆心.
作法:
1、连接AB、BC;
2、分别作AB、BC的垂直
平分线,两线交于O.
A
C
B
·
r
o
结论 :
不在同一直线上的三个点确定 个圆.
一
三角形的外心
3
(1)经过三角形(△ABC)的三个顶点可以作 圆,这个圆叫做三角形的 圆(⊙O) .
(2)外接圆的圆心是三角形三条边的 交点,叫做这个三角形的 .
一个
外接
垂直平分线
外心
到三角形三个顶点的距离相等.
●O
A
B
C
作图:
三角形三边中垂线的交点.
性质:
例2分别画一个锐角三角形、直角三角形和钝角三角形,再画出它们的外接圆,观察并叙述各三角形与它的外心的位置关系.
1.锐角三角形的外心位于三角形内,
2.直角三角形的外心位于直角三角形斜边的中点处,
3.钝角三角形的外心位于三角形外.
A
B
C
●O
A
B
C
C
A
B
┐
●O
●O
反证法
4
1.反证法:不是直接从命题的已知得出结论,而是假设命题的结论 ,由此经过推理得出矛盾,由矛盾断定所作假设不正确,从而得到命题成立.这种证明方法叫做 .
不成立
反证法
假设命题的结论不成立;
从这个假设出发,经过推理,得出矛盾;
由矛盾判定假设不正确,从而肯定命题的结论正确.
2.反证法的一般步骤:
例3 用反证法的证明:经过同一条直线上的点不能作出一个圆.
证明:如图假设过同一直线l上的A、B、C三点可以作一个圆,设这个圆的圆心为P,那么点P既在线段AB的垂直平分线l1,又在线段 的垂直平分线l2,即点P为L1与l2的 点,而l1⊥l,l2⊥l,这与我们以前所学的“过一点有且只
有 条直线与已知直线 ”矛盾.
所以,过同一直线上的三点不能作圆.
BC
交
一
垂直
l1
l2
A
B
C
P
新课讲解
随堂训练
1.⊙O的半径为10cm,A、B、C三点到圆心的距离分别为8cm、10cm、12cm,则点A、B、C与⊙O的位置关系是:
点A在 ;点B在 ;点C在 .
练一练:
圆内
圆上
圆外
2.圆心为O的两个同心圆,半径分别为1和2,若OP= ,则点P在( )
A.在大圆内 B.在小圆内
C.小圆外 D.大圆内、小圆外
o
D
3、体育课上,小王和小孙的铅球成绩分别是6.4m和5.1m,他们投入的铅球分别落在图中哪个区域内?
解:小王投入的铅球落在6-7m的区域内,小孙投入的铅球落在5-6m的区域内.
4.下列说法是否正确?
(1)任意的一个三角形一定有一个外接圆( )
(2)任意一个圆有且只有一个内接三角形( )
(3)经过三点一定可以确定一个圆( )
(4)三角形的外心到三角形各顶点的距离相等( )
√
×
×
√
5.如图,是一块圆形镜片破碎后的部分残片,试找出它的圆心.
A
B
C
O
圆心一定在弦的垂直平分线上.
课堂小结
点与圆的位置关系
点在圆外
点在圆上
点在圆内
d>r
d=r
d
作圆
过一点可以作无数个圆
过两点可以作无数个圆
过不在同一直线上的三个点确定一个圆
直角三角形的外心在斜边中点处
注意:过同一直线上的三个点不能作圆
点P在圆环内
r≤d≤R
R
r
P
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
同课章节目录
