24.4.2 圆锥的侧面积和全面积课件(16张PPT)
文档属性
| 名称 | 24.4.2 圆锥的侧面积和全面积课件(16张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 22.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-24 00:00:00 | ||
图片预览






文档简介
第 二十四章 圆
24.4 弧长和扇形面积
第2课时 圆锥的侧面积和全面积
2020年秋人教版数学九年级上册精品课件
学习目标
1.经历圆锥侧面积的探索过程(难点).
2.会求圆锥的侧面积和全面积,并能解决一些简单的实际问题(重点).
新课导入
问题:观察下面的图形,它们类似我们学过的什么立体图形?你还能举出其他的例子吗?
圆锥
一.圆锥及相关概念
知识讲解
1.圆锥的形成
圆锥的高
母线
S
A
O
B
r
我们把连接圆锥的顶点S和底面圆上任一点的连线SA,SB 等叫做圆锥的母线.
2.圆锥的母线
圆锥有无数条母线,它们都相等.
3.圆锥的高
从圆锥的顶点到圆锥底面圆心之间的距离是圆锥的高.
4.重要数量关系
如果用r表示圆锥底面的半径, h表示圆锥的高线长, l表示圆锥的母线长,那么r、h、l 之间数量关系:
h
O
r
r2+h2= 2
二.圆锥的侧面展开图
问题1:沿着圆锥的母线,把一个圆锥的侧面展开,得到一个扇形,这个扇形的弧长与底面的周长有什么关系?
问题2:圆锥侧面展开图是扇形,这个扇形的半径与圆锥中的哪一条线段相等?
扇形
l
o
侧面
展开图
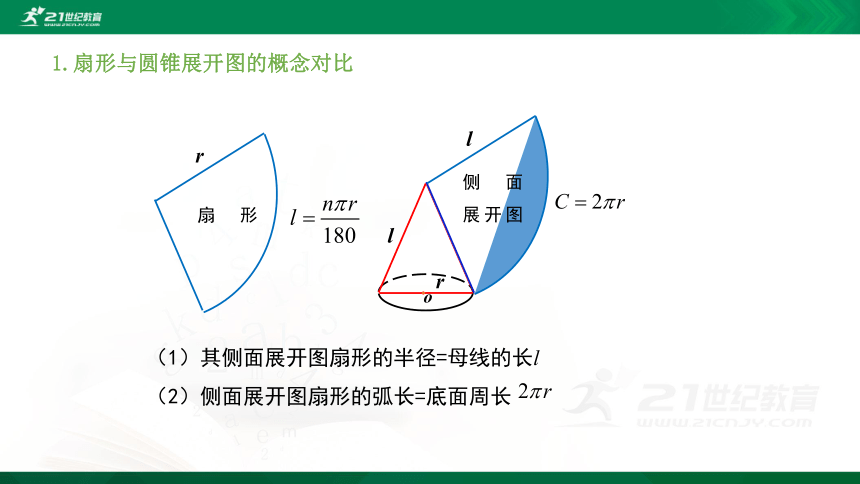
1.扇形与圆锥展开图的概念对比
r
l
r
扇形
(1)其侧面展开图扇形的半径=母线的长l
(2)侧面展开图扇形的弧长=底面周长
2.圆锥的侧面积计算公式
l
o
侧面
展开图
l
r
3.圆锥的全面积计算公式
(r表示圆锥底面的半径, l 表示圆锥的母线长 )
例 蒙古包可以近似地看作由圆锥和圆柱组成,如果想用毛毡搭建20个底面积为12m2,高为3.2m,外围高为1.8m的蒙古包,至少需要多少平方米的毛毡(π取3.142,结果取整数)?
解:下图是一个蒙古包示意图.
根据题意,下部圆柱的底面积为12m2,高h2=1.8m;上部圆锥的高h1=3.2-1.8=1.4(m).
圆柱的底面圆的半径
圆锥的母线长为
侧面积为2π×1.954×1.8≈22.10(m2),
侧面展开扇形的弧长为
圆锥的侧面积为
因此,搭建20个这样的蒙古包至少需要毛毡20×(22.10+14.76)≈738(m2).
h1
h2
r
随堂训练
2.已知一个圆锥的底面半径为12cm,母线长为20cm,则这个圆锥的侧面积为 ,全面积为 .
1.一个圆锥形的冰淇淋纸筒,其底面直径为6cm, 高为4cm,围成这样的冰淇淋纸筒所需纸片的面积为( )
B.
C. D.
D
3.圆锥的母线长为3????????,底面半径为1????????,则此圆锥的侧面积为 ????????2.
4.圆锥的母线长为13????????,底面半径为5????????,则此圆锥的高线为 ????????.
5.已知圆锥的底面半径为3 , 母线长为12 , 那么圆锥侧面展开图所成扇形的圆心角为 .
?
12
6.已知圆锥的底面的半径为3cm,高为4cm,则它的侧面积是 ,全面积是 .
15πcm2
24πcm2
课堂小结
r2+h2=l2
S圆锥侧=πrl
S 圆锥全= S圆锥侧+ S圆锥底= πrl+πr2
圆锥的高
母线
r
S
A
O
B
h
l
o
侧面
展开图
r
底面
(1)侧面展开图扇形的半径=母线的长l
(2)侧面展开图扇形的弧长=底面周长2πr
重要图形
重要结论
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
24.4 弧长和扇形面积
第2课时 圆锥的侧面积和全面积
2020年秋人教版数学九年级上册精品课件
学习目标
1.经历圆锥侧面积的探索过程(难点).
2.会求圆锥的侧面积和全面积,并能解决一些简单的实际问题(重点).
新课导入
问题:观察下面的图形,它们类似我们学过的什么立体图形?你还能举出其他的例子吗?
圆锥
一.圆锥及相关概念
知识讲解
1.圆锥的形成
圆锥的高
母线
S
A
O
B
r
我们把连接圆锥的顶点S和底面圆上任一点的连线SA,SB 等叫做圆锥的母线.
2.圆锥的母线
圆锥有无数条母线,它们都相等.
3.圆锥的高
从圆锥的顶点到圆锥底面圆心之间的距离是圆锥的高.
4.重要数量关系
如果用r表示圆锥底面的半径, h表示圆锥的高线长, l表示圆锥的母线长,那么r、h、l 之间数量关系:
h
O
r
r2+h2= 2
二.圆锥的侧面展开图
问题1:沿着圆锥的母线,把一个圆锥的侧面展开,得到一个扇形,这个扇形的弧长与底面的周长有什么关系?
问题2:圆锥侧面展开图是扇形,这个扇形的半径与圆锥中的哪一条线段相等?
扇形
l
o
侧面
展开图
1.扇形与圆锥展开图的概念对比
r
l
r
扇形
(1)其侧面展开图扇形的半径=母线的长l
(2)侧面展开图扇形的弧长=底面周长
2.圆锥的侧面积计算公式
l
o
侧面
展开图
l
r
3.圆锥的全面积计算公式
(r表示圆锥底面的半径, l 表示圆锥的母线长 )
例 蒙古包可以近似地看作由圆锥和圆柱组成,如果想用毛毡搭建20个底面积为12m2,高为3.2m,外围高为1.8m的蒙古包,至少需要多少平方米的毛毡(π取3.142,结果取整数)?
解:下图是一个蒙古包示意图.
根据题意,下部圆柱的底面积为12m2,高h2=1.8m;上部圆锥的高h1=3.2-1.8=1.4(m).
圆柱的底面圆的半径
圆锥的母线长为
侧面积为2π×1.954×1.8≈22.10(m2),
侧面展开扇形的弧长为
圆锥的侧面积为
因此,搭建20个这样的蒙古包至少需要毛毡20×(22.10+14.76)≈738(m2).
h1
h2
r
随堂训练
2.已知一个圆锥的底面半径为12cm,母线长为20cm,则这个圆锥的侧面积为 ,全面积为 .
1.一个圆锥形的冰淇淋纸筒,其底面直径为6cm, 高为4cm,围成这样的冰淇淋纸筒所需纸片的面积为( )
B.
C. D.
D
3.圆锥的母线长为3????????,底面半径为1????????,则此圆锥的侧面积为 ????????2.
4.圆锥的母线长为13????????,底面半径为5????????,则此圆锥的高线为 ????????.
5.已知圆锥的底面半径为3 , 母线长为12 , 那么圆锥侧面展开图所成扇形的圆心角为 .
?
12
6.已知圆锥的底面的半径为3cm,高为4cm,则它的侧面积是 ,全面积是 .
15πcm2
24πcm2
课堂小结
r2+h2=l2
S圆锥侧=πrl
S 圆锥全= S圆锥侧+ S圆锥底= πrl+πr2
圆锥的高
母线
r
S
A
O
B
h
l
o
侧面
展开图
r
底面
(1)侧面展开图扇形的半径=母线的长l
(2)侧面展开图扇形的弧长=底面周长2πr
重要图形
重要结论
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
同课章节目录
