人教a版 必修二 第一章 1.2 1.2.1 中心投影与平行投影及空间几何体的三视图 配套课件
文档属性
| 名称 | 人教a版 必修二 第一章 1.2 1.2.1 中心投影与平行投影及空间几何体的三视图 配套课件 |  | |
| 格式 | rar | ||
| 文件大小 | 631.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-08-04 09:02:27 | ||
图片预览


文档简介
(共17张PPT)
1.2 空间几何体的三视图和直观图
1.2.1 中心投影与平行投影及空间几何体的三视图
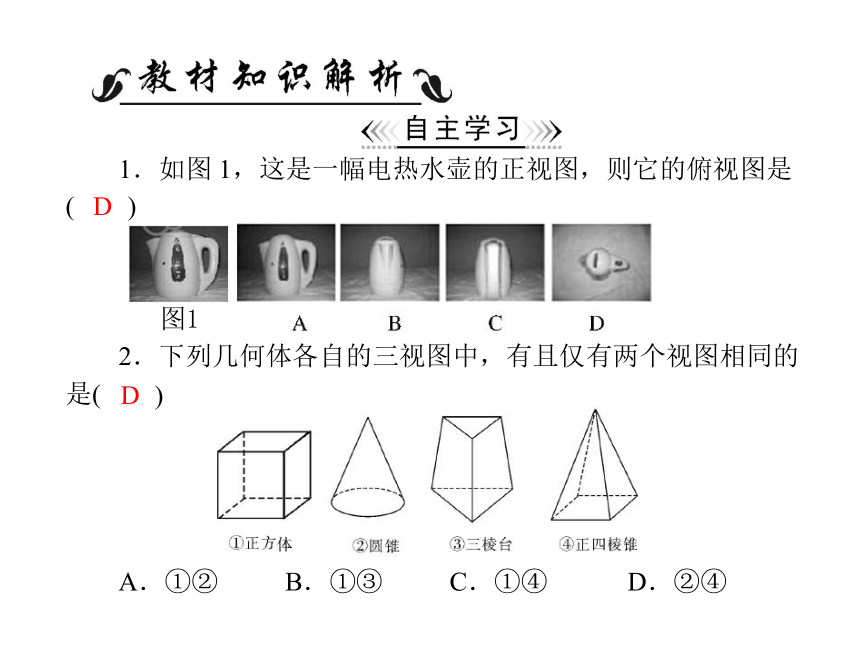
1.如图 1,这是一幅电热水壶的正视图,则它的俯视图是
(
)
D
2.下列几何体各自的三视图中,有且仅有两个视图相同的
是(
)
D
A.①②
B.①③
C.①④
D.②④
图1
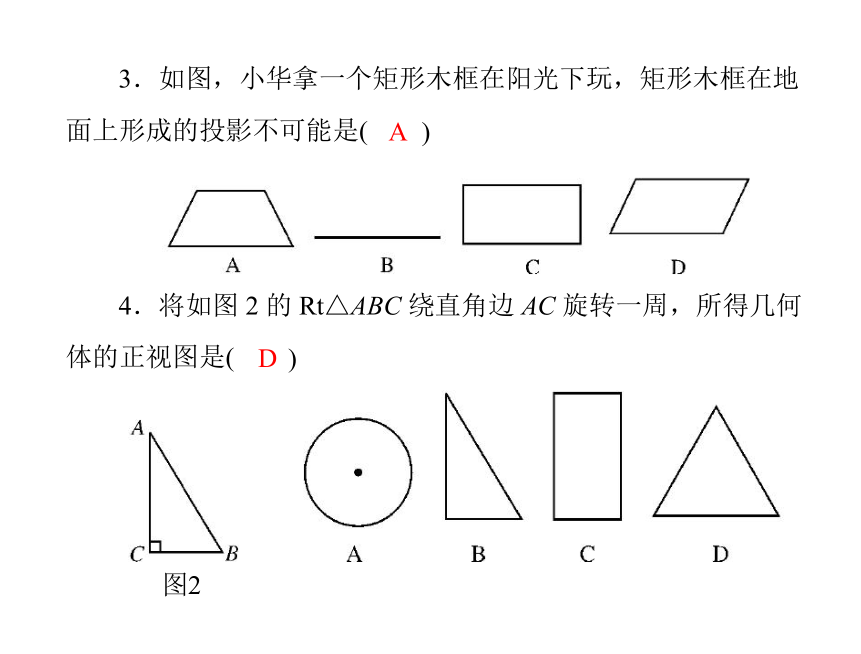
3.如图,小华拿一个矩形木框在阳光下玩,矩形木框在地
面上形成的投影不可能是(
)
A
4.将如图 2 的 Rt△ABC 绕直角边 AC 旋转一周,所得几何
体的正视图是(
)
D
图2
重点
空间几何体的三视图
1.光线从几何体的前面向后投影所得的投影图成为“正视
图”,自左向右投影所得的投影图称为“侧视图”,自上向下投
影所得的图形称为“俯视图”.用这三种视图即可刻划空间物
体的几何结构,称为“三视图”.
2.球的正视图、侧视图、俯视图都是圆;正方体的正视图、
侧视图、俯视图都是正方形.
3.画三视图应遵循“长对正、高平齐、宽相等”的原则,即
“正、俯视图一样长,正、侧视图一样高,俯、侧视图一样宽”.
4.将三视图还原成空间几何体,应充分抓住正视图的结构特
征及俯视图与侧视图的结构特点进行逆向思维,并联想基本的
几何体的图形结构.
简单几何体的三视图
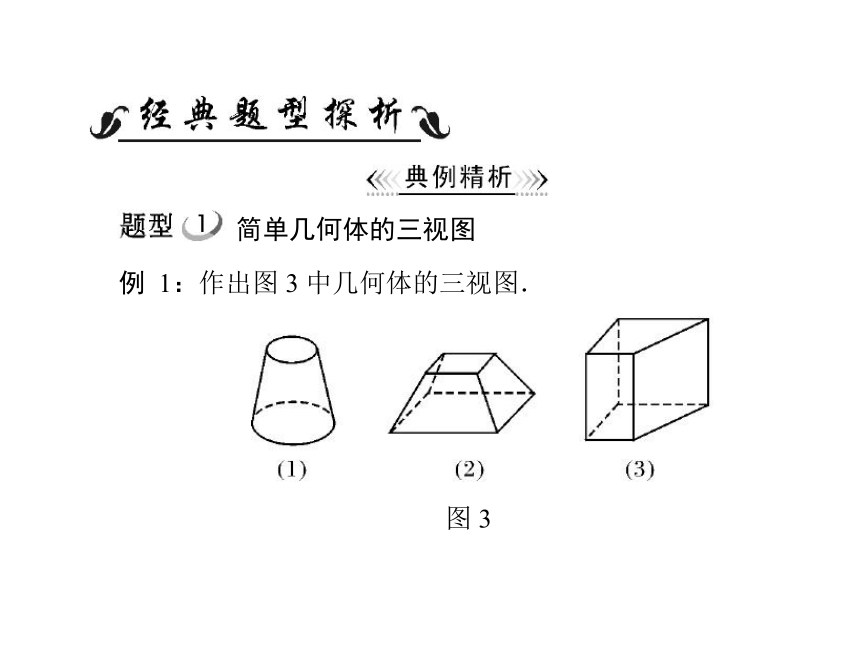
例 1:作出图 3 中几何体的三视图.
图 3
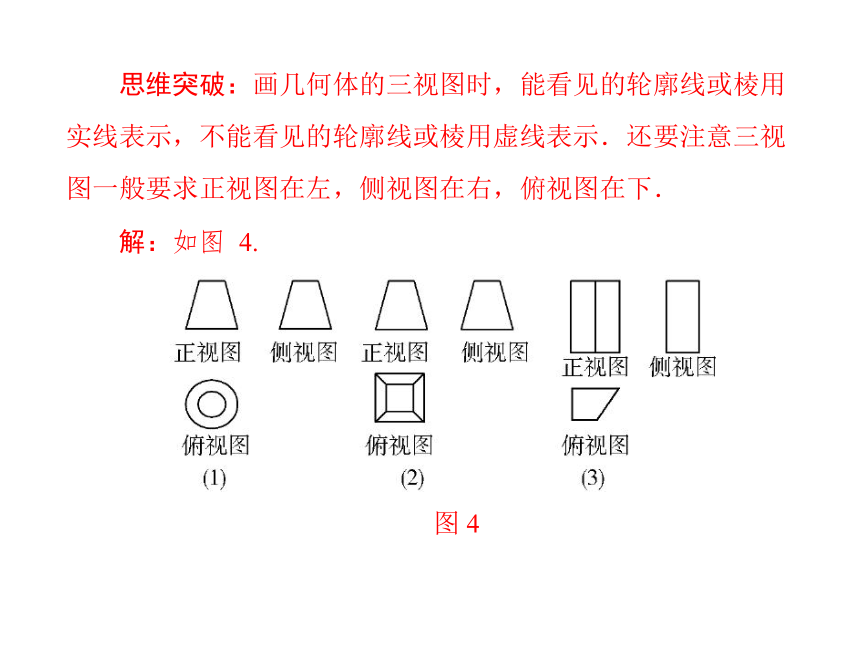
思维突破:画几何体的三视图时,能看见的轮廓线或棱用
实线表示,不能看见的轮廓线或棱用虚线表示.还要注意三视
图一般要求正视图在左,侧视图在右,俯视图在下.
解:如图 4.
图 4
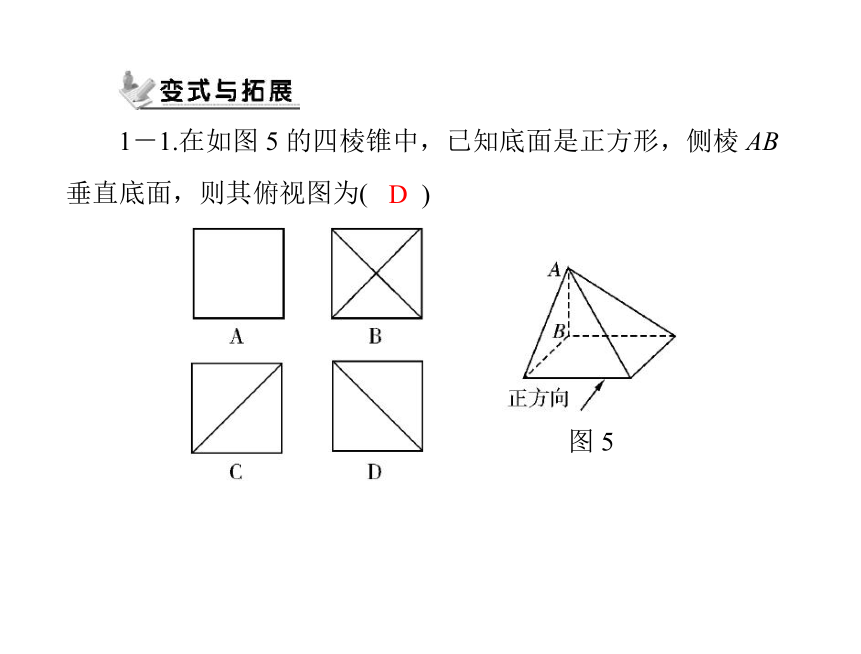
1-1.在如图 5 的四棱锥中,已知底面是正方形,侧棱 AB
垂直底面,则其俯视图为(
)
D
图 5
1-2.一物体及其正视图如图 6,则它的侧视图与俯视图分
别是图形中的(
)
B
图 6
A.①②
B.③②
C.①④
D.③④
简单组合体的三视图
例 2:画出图 7 中组合体的三视图.
图 7
解:如图 8.
图 8
画组合体的三视图时,要注意相邻两个几
何体的表面相交,表面的交线是它们的分界线,在三视图中不
要忘记将它们画出来,还要注意是虚线还是实线.
解:如图 4.
图 4
2-1.画出如图 9 中几何体的三视图.
图 9
2-2.下列三视图所对应的直观图是(
)
C
由三视图还原几何体
例 3:如图 10 中的是一些立体图形的三视图,请说出立体
图形的名称.
图 10
解:分别为长方体、圆锥.
3-1.如图 11,找出相应的立体图,并在其下方括号内填写
它的序号:
图 11
解:依次从每个几何体的三个方向得到三视图,再与已知
三视图比较,所以依次为 C、A、D、B.
例 4: 如图 12,根据几何体,在相应的视图中补上缺少的线
条.
图 12
错因剖析:没有充分观察几何体,忘记不能看得见的轮廓
线或棱用虚线表示.
正解:如图13.
图 13
4-1.(2010 年北京)一个长方体去掉一个小长方体,所得几
何体的正(主)视图与侧(左)视图分别如图 14,则该几何体的俯视
图为(
)
图 14
答案:C
1.2 空间几何体的三视图和直观图
1.2.1 中心投影与平行投影及空间几何体的三视图
1.如图 1,这是一幅电热水壶的正视图,则它的俯视图是
(
)
D
2.下列几何体各自的三视图中,有且仅有两个视图相同的
是(
)
D
A.①②
B.①③
C.①④
D.②④
图1
3.如图,小华拿一个矩形木框在阳光下玩,矩形木框在地
面上形成的投影不可能是(
)
A
4.将如图 2 的 Rt△ABC 绕直角边 AC 旋转一周,所得几何
体的正视图是(
)
D
图2
重点
空间几何体的三视图
1.光线从几何体的前面向后投影所得的投影图成为“正视
图”,自左向右投影所得的投影图称为“侧视图”,自上向下投
影所得的图形称为“俯视图”.用这三种视图即可刻划空间物
体的几何结构,称为“三视图”.
2.球的正视图、侧视图、俯视图都是圆;正方体的正视图、
侧视图、俯视图都是正方形.
3.画三视图应遵循“长对正、高平齐、宽相等”的原则,即
“正、俯视图一样长,正、侧视图一样高,俯、侧视图一样宽”.
4.将三视图还原成空间几何体,应充分抓住正视图的结构特
征及俯视图与侧视图的结构特点进行逆向思维,并联想基本的
几何体的图形结构.
简单几何体的三视图
例 1:作出图 3 中几何体的三视图.
图 3
思维突破:画几何体的三视图时,能看见的轮廓线或棱用
实线表示,不能看见的轮廓线或棱用虚线表示.还要注意三视
图一般要求正视图在左,侧视图在右,俯视图在下.
解:如图 4.
图 4
1-1.在如图 5 的四棱锥中,已知底面是正方形,侧棱 AB
垂直底面,则其俯视图为(
)
D
图 5
1-2.一物体及其正视图如图 6,则它的侧视图与俯视图分
别是图形中的(
)
B
图 6
A.①②
B.③②
C.①④
D.③④
简单组合体的三视图
例 2:画出图 7 中组合体的三视图.
图 7
解:如图 8.
图 8
画组合体的三视图时,要注意相邻两个几
何体的表面相交,表面的交线是它们的分界线,在三视图中不
要忘记将它们画出来,还要注意是虚线还是实线.
解:如图 4.
图 4
2-1.画出如图 9 中几何体的三视图.
图 9
2-2.下列三视图所对应的直观图是(
)
C
由三视图还原几何体
例 3:如图 10 中的是一些立体图形的三视图,请说出立体
图形的名称.
图 10
解:分别为长方体、圆锥.
3-1.如图 11,找出相应的立体图,并在其下方括号内填写
它的序号:
图 11
解:依次从每个几何体的三个方向得到三视图,再与已知
三视图比较,所以依次为 C、A、D、B.
例 4: 如图 12,根据几何体,在相应的视图中补上缺少的线
条.
图 12
错因剖析:没有充分观察几何体,忘记不能看得见的轮廓
线或棱用虚线表示.
正解:如图13.
图 13
4-1.(2010 年北京)一个长方体去掉一个小长方体,所得几
何体的正(主)视图与侧(左)视图分别如图 14,则该几何体的俯视
图为(
)
图 14
答案:C
