人教a版 必修二 第一章 1.3 1.3.1 柱体、锥体、台体的表面积 配套课件
文档属性
| 名称 | 人教a版 必修二 第一章 1.3 1.3.1 柱体、锥体、台体的表面积 配套课件 |

|
|
| 格式 | rar | ||
| 文件大小 | 456.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-08-04 00:00:00 | ||
图片预览




文档简介
(共19张PPT)
1.3 空间几何体的表面积与体积
1.3.1 柱体、锥体、台体的表面积
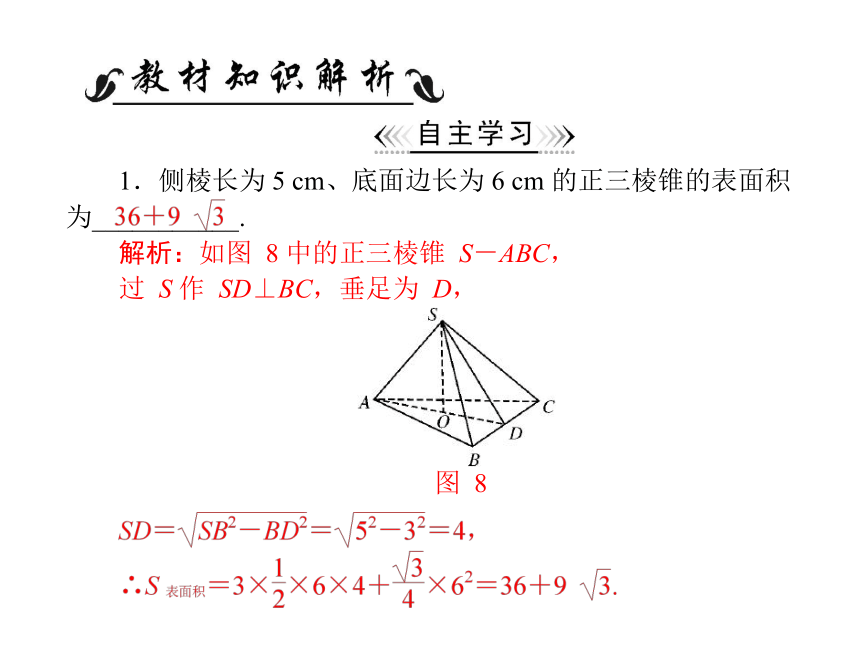
1.侧棱长为 5 cm、底面边长为 6 cm 的正三棱锥的表面积
为___________.
解析:如图 8 中的正三棱锥 S-ABC,
过 S 作 SD⊥BC,垂足为 D,
图 8
2.已知正四棱台的上、下底面的边长分别是 4 cm 和 8 cm,
侧棱长为 8 cm,则正四棱台的表面积为____________.
图 9
解析:如图 9,在正四棱台 ABCD-A1B1C1D1,
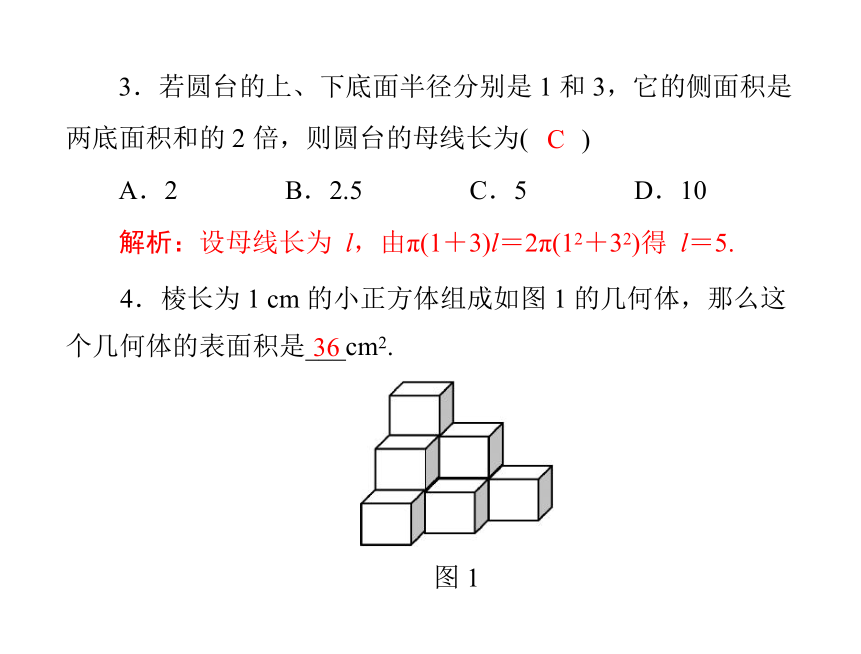
3.若圆台的上、下底面半径分别是 1 和 3,它的侧面积是
两底面积和的 2 倍,则圆台的母线长为(
)
C
A.2
B.2.5
C.5
D.10
解析:设母线长为 l,由π(1+3)l=2π(12+32)得 l=5.
36
个几何体的表面积是___cm2.
图 1
4.棱长为 1 cm 的小正方体组成如图 1 的几何体,那么这
重点
柱、锥、台的表面积公式及应用
1.已知正方体的棱长为 a,则正方体的表面积是 6a2;已知
长方体的长、宽、高分别是 a、b、c,则该长方体的表面积是
2(ab+bc+ac).
2.(1)圆柱的侧面展开图是矩形,当底面半径为 r,母线长为
l 时,圆柱的表面积为 S=2πr2+2πrl;
(2)圆锥的侧面展开图是扇形,当底面半径为 r,母线长为 l
时,圆锥的表面积为 S=πr2+πrl;
(3)圆台的侧面展开图是扇环,当上、下底面半径分别为 r′、
r,母线长为 l 时,圆台的表面积等于上、下两个底面的面积和
加上侧面的面积,即 S=π(r′2+r2+r′l+rl).
难点
圆锥、圆台的侧面展开图
1.圆锥的侧面展开图是扇形,当底面半径为 r,母线长为 l
2.圆台的侧面展开图是扇环,当上、下底面半径分别为 r′、
r,母线长为 l 时,扇环的圆心角θ=
r-r′
l
×360°.
最基本几何体的运算
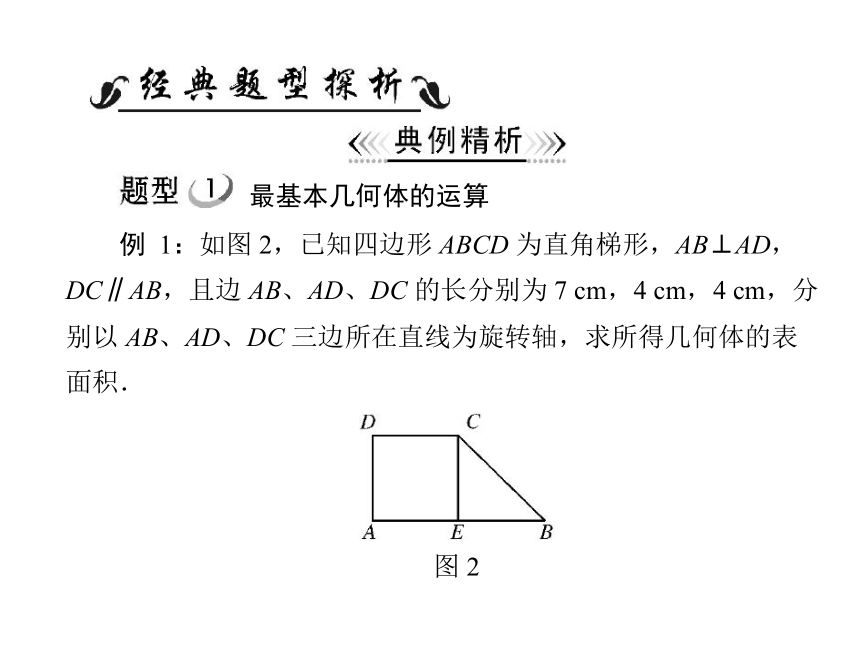
例 1:如图 2,已知四边形 ABCD 为直角梯形,AB⊥AD,
DC∥AB,且边 AB、AD、DC 的长分别为 7 cm,4 cm,4 cm,分
别以 AB、AD、DC 三边所在直线为旋转轴,求所得几何体的表
面积.
图 2
解:作 CE⊥AB 于点 E,
(1)以 AB 所在直线为旋转轴(此时旋转得到一圆锥和一圆柱
的组合体):
S1=8π×4+π×4×5+π×42=68π.
(2)以 AD 所在直线为旋转轴:
S2=π×42+π×72+π×(4+7)×5=120π.
(3)以 DC 所在直线为旋转轴:
S3=5π×4+2π×4×7+π×42=92π.
3×4
,
解:以 AB 所在直线为旋转轴:S=4π(4+5)=36π,
以 AC 所在直线为旋转轴:S=3π(5+3)=24π,
以 BC 所在直线为旋转轴:此时所得几何体为两个圆锥的组
合体,则 BC 边上的高 AD=
5
=
12
5
1-1.已知△ABC 三边 AB、AC、BC 长分别为 3 cm,4 cm,
5 cm,分别以三边所在直线为旋转轴,求所得几何体的表面积.
由三视图求几何体表面积
例 2:一个正三棱柱的三视图如图 3,求这个正三棱柱的表
面积.
图 3
由侧视图知正三棱柱底面三角形的高为
解:由三视图知正三棱柱的高为 2 mm.
利用三视图求几何体表面积的关键,是正
确理解和认识三视图中所给量与几何体中量之间的对应关系.
∴正三棱柱的表面积为
2-1.(2010 年安徽)一个几何体的三视图如图 4,该几何体
)
B
的表面积是(
A.372
C.292
图 4
B.360
D.280
几何体表面积的最值问题
例 3:如图 5,圆台上、下底面半径分别为 5 cm,10 cm,母
线长为 20 cm,从母线 AB 的中点 M 拉一条细绳,围绕圆台侧面
转至下底面的 B 点,求 B、M 间细绳的最短长度.
图 5
,∴SA=20 cm.
解:如图 6,沿 BA 所在母线将其展开,易知最短长度即为
线段 B、M 的长度.
设圆锥顶点为 S,△SBC 是其轴截面,则
5
10
=
SA
SA+20
∴△MSB′是直角三角形.
图 6
=50(cm).
即 M、B 间细绳的最短长度为 50 cm.
求旋转体或多面体侧面上两点间的最短距
离的思路:将其转化为平面图形,在平面图形上求出的两点间
线段的长度就是两点间的最短距离.
图 7
解:沿 A、B 所在棱将三棱锥侧面展开,则 A、B 两点间的
最短绳长就是线段 AB 的长度.
又 OA=4 cm,OB=3 cm,∠AOB=90°,
∴AB=5 cm.
故此绳在 A、B 间最短的绳长为 5 cm.
3-1.如图 7,在以 O 为顶点的三棱锥中,过 O 的三条棱两
两的交角都是 30°,在一条棱上有 A、B 两点,OA=4 cm,OB
=3 cm,以 A、B 为端点用一条绳子紧绕三棱锥的侧面一周(绳
和侧面无摩擦),求此绳在 A、B 之间的最短绳长.
例 4:用一张长为 8 cm,宽为 4 cm 的矩形硬纸卷成圆柱的
侧面,求圆柱的轴截面的面积和底面积.
错因剖析:将矩形硬纸卷成圆柱有两种不同卷法,很容易
丢解.
正解:设卷成的圆柱的母线长(即高)为 h,
底面半径为 r,则
4-1.圆柱的一个底面积为 S,侧面展开图为一个正方形,
)
那么这个圆柱的侧面积是(
A.4πS
B.2πS
C.πS
A
解析:设底面半径为 r,故 S=πr2.由侧面展开图是正方形,
1.3 空间几何体的表面积与体积
1.3.1 柱体、锥体、台体的表面积
1.侧棱长为 5 cm、底面边长为 6 cm 的正三棱锥的表面积
为___________.
解析:如图 8 中的正三棱锥 S-ABC,
过 S 作 SD⊥BC,垂足为 D,
图 8
2.已知正四棱台的上、下底面的边长分别是 4 cm 和 8 cm,
侧棱长为 8 cm,则正四棱台的表面积为____________.
图 9
解析:如图 9,在正四棱台 ABCD-A1B1C1D1,
3.若圆台的上、下底面半径分别是 1 和 3,它的侧面积是
两底面积和的 2 倍,则圆台的母线长为(
)
C
A.2
B.2.5
C.5
D.10
解析:设母线长为 l,由π(1+3)l=2π(12+32)得 l=5.
36
个几何体的表面积是___cm2.
图 1
4.棱长为 1 cm 的小正方体组成如图 1 的几何体,那么这
重点
柱、锥、台的表面积公式及应用
1.已知正方体的棱长为 a,则正方体的表面积是 6a2;已知
长方体的长、宽、高分别是 a、b、c,则该长方体的表面积是
2(ab+bc+ac).
2.(1)圆柱的侧面展开图是矩形,当底面半径为 r,母线长为
l 时,圆柱的表面积为 S=2πr2+2πrl;
(2)圆锥的侧面展开图是扇形,当底面半径为 r,母线长为 l
时,圆锥的表面积为 S=πr2+πrl;
(3)圆台的侧面展开图是扇环,当上、下底面半径分别为 r′、
r,母线长为 l 时,圆台的表面积等于上、下两个底面的面积和
加上侧面的面积,即 S=π(r′2+r2+r′l+rl).
难点
圆锥、圆台的侧面展开图
1.圆锥的侧面展开图是扇形,当底面半径为 r,母线长为 l
2.圆台的侧面展开图是扇环,当上、下底面半径分别为 r′、
r,母线长为 l 时,扇环的圆心角θ=
r-r′
l
×360°.
最基本几何体的运算
例 1:如图 2,已知四边形 ABCD 为直角梯形,AB⊥AD,
DC∥AB,且边 AB、AD、DC 的长分别为 7 cm,4 cm,4 cm,分
别以 AB、AD、DC 三边所在直线为旋转轴,求所得几何体的表
面积.
图 2
解:作 CE⊥AB 于点 E,
(1)以 AB 所在直线为旋转轴(此时旋转得到一圆锥和一圆柱
的组合体):
S1=8π×4+π×4×5+π×42=68π.
(2)以 AD 所在直线为旋转轴:
S2=π×42+π×72+π×(4+7)×5=120π.
(3)以 DC 所在直线为旋转轴:
S3=5π×4+2π×4×7+π×42=92π.
3×4
,
解:以 AB 所在直线为旋转轴:S=4π(4+5)=36π,
以 AC 所在直线为旋转轴:S=3π(5+3)=24π,
以 BC 所在直线为旋转轴:此时所得几何体为两个圆锥的组
合体,则 BC 边上的高 AD=
5
=
12
5
1-1.已知△ABC 三边 AB、AC、BC 长分别为 3 cm,4 cm,
5 cm,分别以三边所在直线为旋转轴,求所得几何体的表面积.
由三视图求几何体表面积
例 2:一个正三棱柱的三视图如图 3,求这个正三棱柱的表
面积.
图 3
由侧视图知正三棱柱底面三角形的高为
解:由三视图知正三棱柱的高为 2 mm.
利用三视图求几何体表面积的关键,是正
确理解和认识三视图中所给量与几何体中量之间的对应关系.
∴正三棱柱的表面积为
2-1.(2010 年安徽)一个几何体的三视图如图 4,该几何体
)
B
的表面积是(
A.372
C.292
图 4
B.360
D.280
几何体表面积的最值问题
例 3:如图 5,圆台上、下底面半径分别为 5 cm,10 cm,母
线长为 20 cm,从母线 AB 的中点 M 拉一条细绳,围绕圆台侧面
转至下底面的 B 点,求 B、M 间细绳的最短长度.
图 5
,∴SA=20 cm.
解:如图 6,沿 BA 所在母线将其展开,易知最短长度即为
线段 B、M 的长度.
设圆锥顶点为 S,△SBC 是其轴截面,则
5
10
=
SA
SA+20
∴△MSB′是直角三角形.
图 6
=50(cm).
即 M、B 间细绳的最短长度为 50 cm.
求旋转体或多面体侧面上两点间的最短距
离的思路:将其转化为平面图形,在平面图形上求出的两点间
线段的长度就是两点间的最短距离.
图 7
解:沿 A、B 所在棱将三棱锥侧面展开,则 A、B 两点间的
最短绳长就是线段 AB 的长度.
又 OA=4 cm,OB=3 cm,∠AOB=90°,
∴AB=5 cm.
故此绳在 A、B 间最短的绳长为 5 cm.
3-1.如图 7,在以 O 为顶点的三棱锥中,过 O 的三条棱两
两的交角都是 30°,在一条棱上有 A、B 两点,OA=4 cm,OB
=3 cm,以 A、B 为端点用一条绳子紧绕三棱锥的侧面一周(绳
和侧面无摩擦),求此绳在 A、B 之间的最短绳长.
例 4:用一张长为 8 cm,宽为 4 cm 的矩形硬纸卷成圆柱的
侧面,求圆柱的轴截面的面积和底面积.
错因剖析:将矩形硬纸卷成圆柱有两种不同卷法,很容易
丢解.
正解:设卷成的圆柱的母线长(即高)为 h,
底面半径为 r,则
4-1.圆柱的一个底面积为 S,侧面展开图为一个正方形,
)
那么这个圆柱的侧面积是(
A.4πS
B.2πS
C.πS
A
解析:设底面半径为 r,故 S=πr2.由侧面展开图是正方形,
