人教版数学八年级上册11.2.1 三角形内角和定理课件(共16张PPT)
文档属性
| 名称 | 人教版数学八年级上册11.2.1 三角形内角和定理课件(共16张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-23 00:00:00 | ||
图片预览


文档简介
三角形内角和定理
学习目标
如何证明三角形内角和是180°?
能运用三角形内角和定理解决相关的求角度问题.
知识精讲
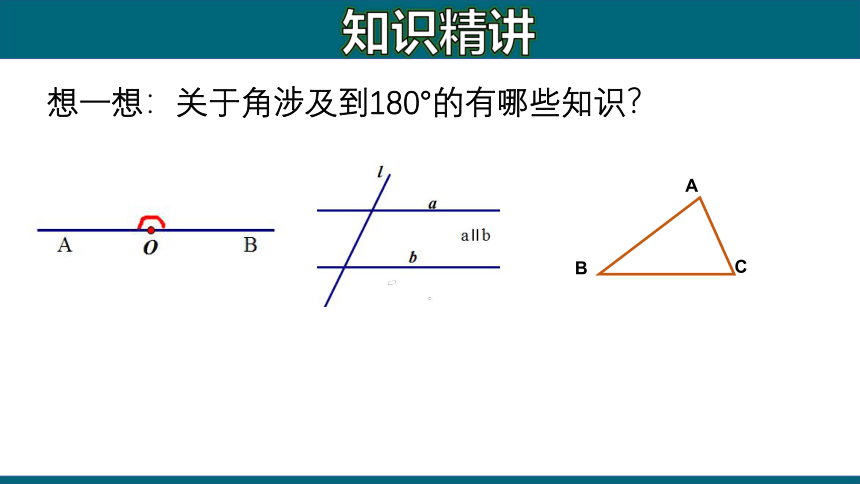
想一想:关于角涉及到180°的有哪些知识?
A
B
C
知识精讲
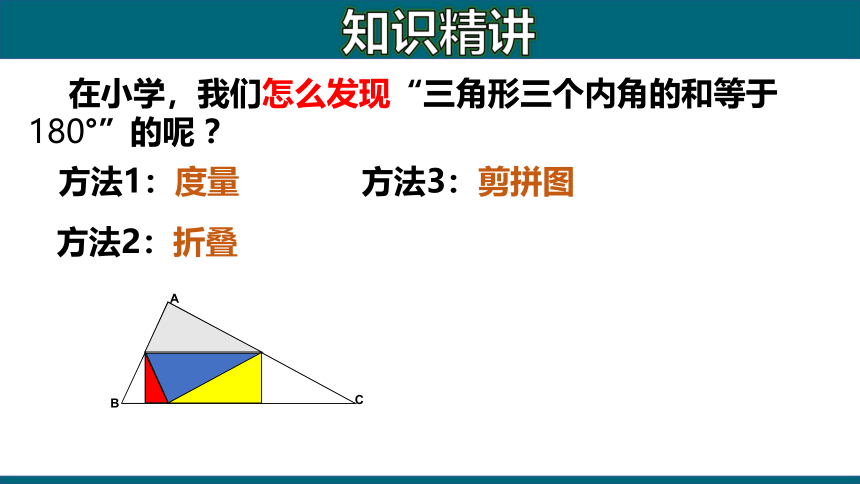
在小学,我们怎么发现“三角形三个内角的和等于180°”的呢 ?
方法1:度量
方法2:折叠
方法3:剪拼图
A
B
C
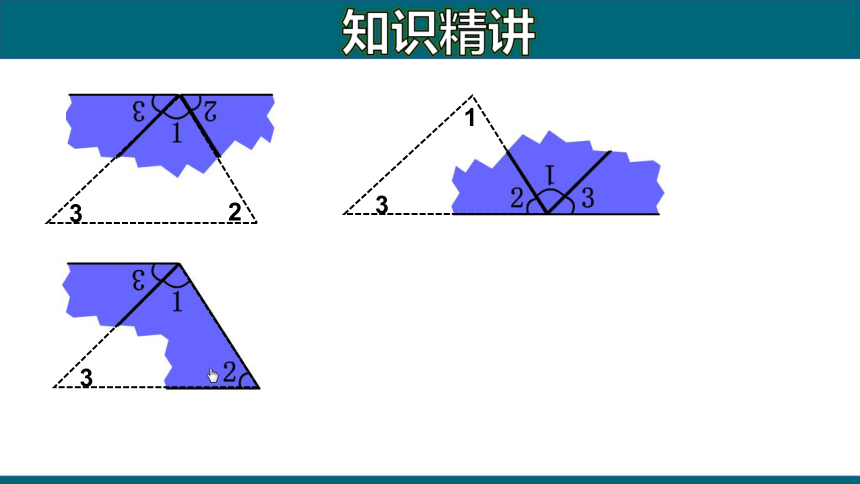
知识精讲
3
2
3
1
3
知识精讲
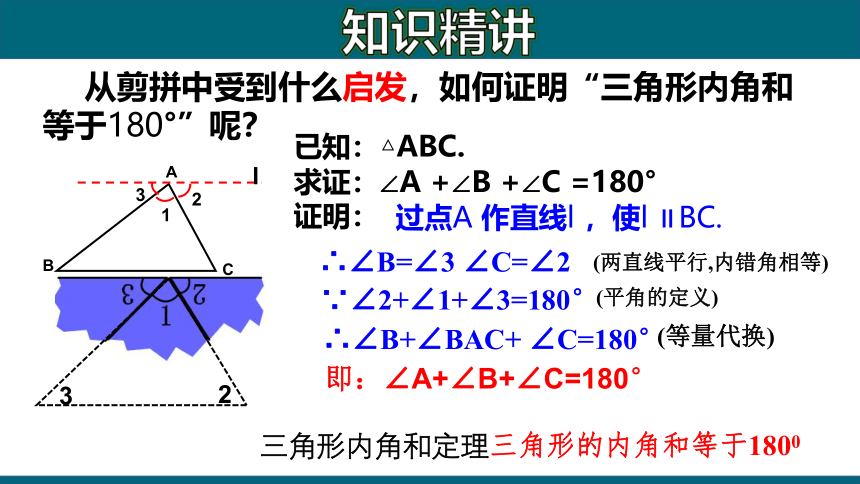
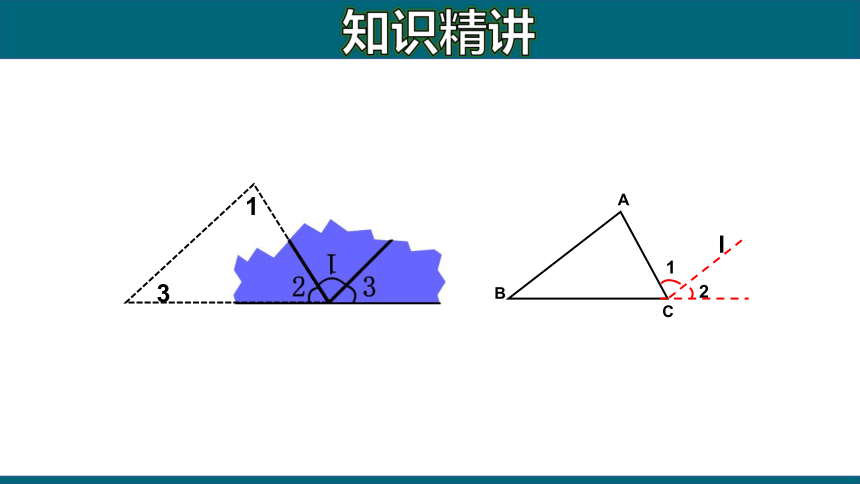
从剪拼中受到什么启发,如何证明“三角形内角和等于180°”呢?
3
2
A
B
C
l
3
2
1
过点A 作直线l ,使l ∥BC.
三角形内角和定理三角形的内角和等于1800
已知:△ABC.
求证:∠A +∠B +∠C =180°
证明:
∴∠B=∠3 ∠C=∠2
(两直线平行,内错角相等)
∵∠2+∠1+∠3=180°
∴∠B+∠BAC+ ∠C=180°
(平角的定义)
(等量代换)
即:∠A+∠B+∠C=180°
知识精讲
1
3
2
B
A
C
1
l
知识精讲
3
1
l
B
A
C
如图,在△ABC 中, ∠BAC =40°, ∠B = 75°,AD 是△ABC 的角平分线.求∠ADB 的度数 .
D
C
B
A
由∠BAC=40°,AD是
△ ABC的角平分线,
得∠BAD= ∠BAC=20°.
在△ ABD中,
∠ADB =180°-∠B-∠BAD
= 180° - 75°- 20°=85°.
解:
典例解析
如图,C 岛在A 岛的北偏东50°方向,B 岛在A 岛的北偏东80°方向,C 岛在B 岛的北偏西40°方向.从B 岛看A,C 两岛的视角∠ABC 是多少度?从C岛看A,B 两岛的视角∠ACB 呢?
北
北
C
A
B
D
E
实际应用
如图,C 岛在A 岛的北偏东50°方向,B 岛在A 岛的北偏东80°方向,C 岛在B 岛的北偏西40°方向.从B 岛看A,C 两岛的视角∠ABC 是多少度?从C岛看A,B 两岛的视角∠ACB 呢?
解:∵∠DAB=80°,∠DAC=50°,
∴∠CAB=∠DAB-∠DAC=30°
由题意知AD∥BE,∠DAB=80°,
∴∠EBA=180°-∠DAB=180°-80°=100°
∵∠EBC=40°,
∴∠ABC=∠EBA-∠EBC=60°.
在△ABC中,∠ACB=180°-∠CAB-∠ABC
=180°-30°-60°=90°
北
北
C
A
B
D
E
50°
40°
实际应用
巩固练习
1、(口答)下列各组角是同一个三角形的内角吗?为什么?
(2)60°, 40°, 90°
(3)30°, 60°, 50°
(1)3°, 150°, 27°
(是 )
( 不是)
( 不是)
(1)在△ABC中,∠A=35°,∠ B=43 °
则∠ C= .
(2)在△ABC中, ∠A :∠B:∠C=2:3:4
则∠A = ∠ B= ∠ C= .
102 °
80 °
60 °
40 °
2、填空
巩固练习
(3)一个三角形中最多有 个直角?为什么?
(4)一个三角形中最多有 个钝角?为什么?
(5)一个三角形中至少有 个锐角?为什么?
(6)任意一个三角形中,最大的一个角的度数至少为 .
60°
2
1
1
2、填空
巩固练习
小结梳理
运用三角形内角和定理解决相关的求角度问题.
三角形内角和定理
三角形的内角和等于1800
学习目标
如何证明三角形内角和是180°?
能运用三角形内角和定理解决相关的求角度问题.
知识精讲
想一想:关于角涉及到180°的有哪些知识?
A
B
C
知识精讲
在小学,我们怎么发现“三角形三个内角的和等于180°”的呢 ?
方法1:度量
方法2:折叠
方法3:剪拼图
A
B
C
知识精讲
3
2
3
1
3
知识精讲
从剪拼中受到什么启发,如何证明“三角形内角和等于180°”呢?
3
2
A
B
C
l
3
2
1
过点A 作直线l ,使l ∥BC.
三角形内角和定理三角形的内角和等于1800
已知:△ABC.
求证:∠A +∠B +∠C =180°
证明:
∴∠B=∠3 ∠C=∠2
(两直线平行,内错角相等)
∵∠2+∠1+∠3=180°
∴∠B+∠BAC+ ∠C=180°
(平角的定义)
(等量代换)
即:∠A+∠B+∠C=180°
知识精讲
1
3
2
B
A
C
1
l
知识精讲
3
1
l
B
A
C
如图,在△ABC 中, ∠BAC =40°, ∠B = 75°,AD 是△ABC 的角平分线.求∠ADB 的度数 .
D
C
B
A
由∠BAC=40°,AD是
△ ABC的角平分线,
得∠BAD= ∠BAC=20°.
在△ ABD中,
∠ADB =180°-∠B-∠BAD
= 180° - 75°- 20°=85°.
解:
典例解析
如图,C 岛在A 岛的北偏东50°方向,B 岛在A 岛的北偏东80°方向,C 岛在B 岛的北偏西40°方向.从B 岛看A,C 两岛的视角∠ABC 是多少度?从C岛看A,B 两岛的视角∠ACB 呢?
北
北
C
A
B
D
E
实际应用
如图,C 岛在A 岛的北偏东50°方向,B 岛在A 岛的北偏东80°方向,C 岛在B 岛的北偏西40°方向.从B 岛看A,C 两岛的视角∠ABC 是多少度?从C岛看A,B 两岛的视角∠ACB 呢?
解:∵∠DAB=80°,∠DAC=50°,
∴∠CAB=∠DAB-∠DAC=30°
由题意知AD∥BE,∠DAB=80°,
∴∠EBA=180°-∠DAB=180°-80°=100°
∵∠EBC=40°,
∴∠ABC=∠EBA-∠EBC=60°.
在△ABC中,∠ACB=180°-∠CAB-∠ABC
=180°-30°-60°=90°
北
北
C
A
B
D
E
50°
40°
实际应用
巩固练习
1、(口答)下列各组角是同一个三角形的内角吗?为什么?
(2)60°, 40°, 90°
(3)30°, 60°, 50°
(1)3°, 150°, 27°
(是 )
( 不是)
( 不是)
(1)在△ABC中,∠A=35°,∠ B=43 °
则∠ C= .
(2)在△ABC中, ∠A :∠B:∠C=2:3:4
则∠A = ∠ B= ∠ C= .
102 °
80 °
60 °
40 °
2、填空
巩固练习
(3)一个三角形中最多有 个直角?为什么?
(4)一个三角形中最多有 个钝角?为什么?
(5)一个三角形中至少有 个锐角?为什么?
(6)任意一个三角形中,最大的一个角的度数至少为 .
60°
2
1
1
2、填空
巩固练习
小结梳理
运用三角形内角和定理解决相关的求角度问题.
三角形内角和定理
三角形的内角和等于1800
