人教a版 必修二 第一章 章末整合提升 配套课件
文档属性
| 名称 | 人教a版 必修二 第一章 章末整合提升 配套课件 |
|
|
| 格式 | rar | ||
| 文件大小 | 352.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-08-04 00:00:00 | ||
图片预览



文档简介
(共10张PPT)
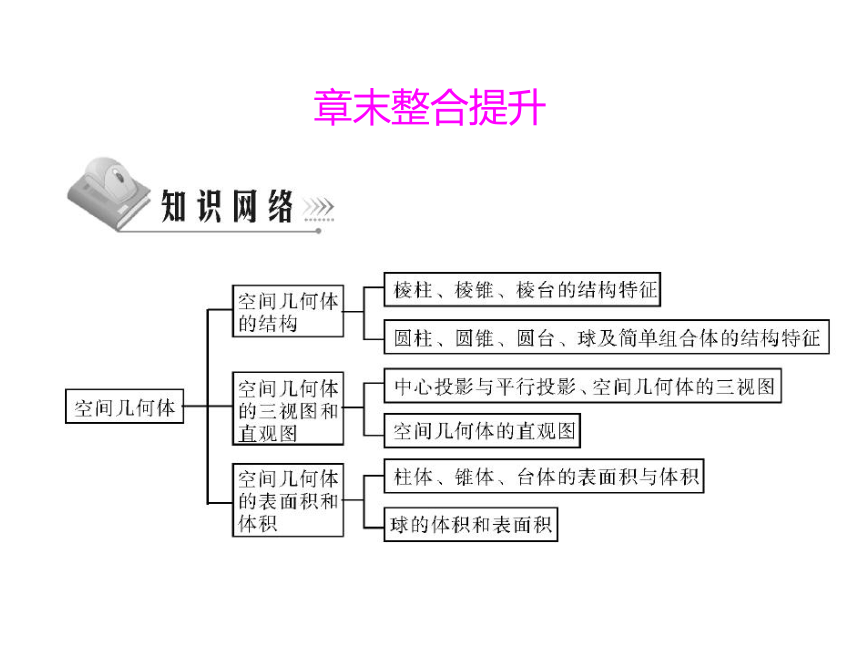
章末整合提升
专题一
三视图的应用
已知几何体的三视图,求该几何体的体积或表面积时,需
先由三视图还原出直观图,再根据直观图求几何体的体积或表
面积.
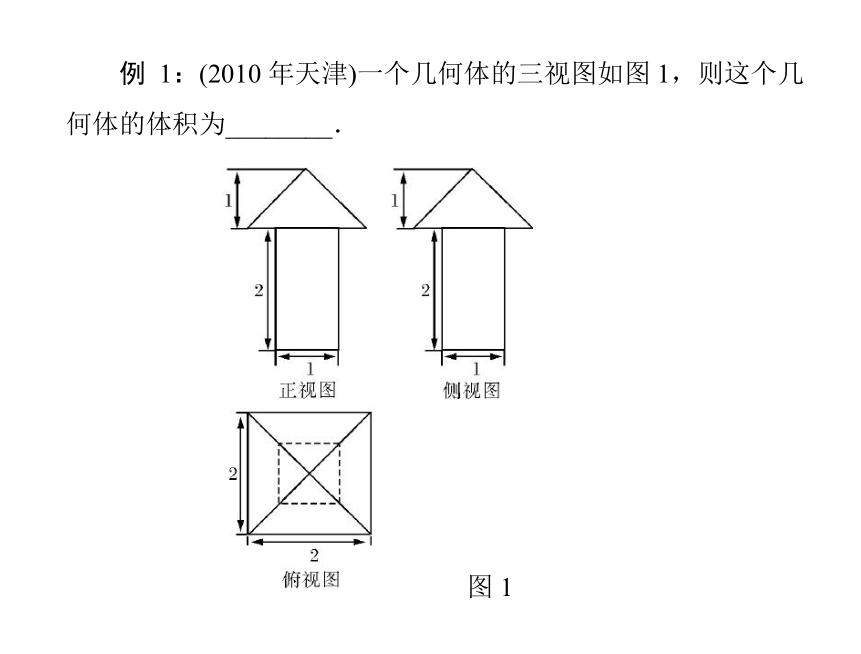
图 1
例 1:(2010 年天津)一个几何体的三视图如图 1,则这个几
何体的体积为________.
答案:
10
3
思维突破:由三视图可得,该几何体由一个正四棱柱和一
个正四棱锥组成,正四棱柱的底面边长为 1,高为 2,正四棱锥
的底面边长为 2 ,高为 1 ,故该几何体的体积 V =1×1×2 +
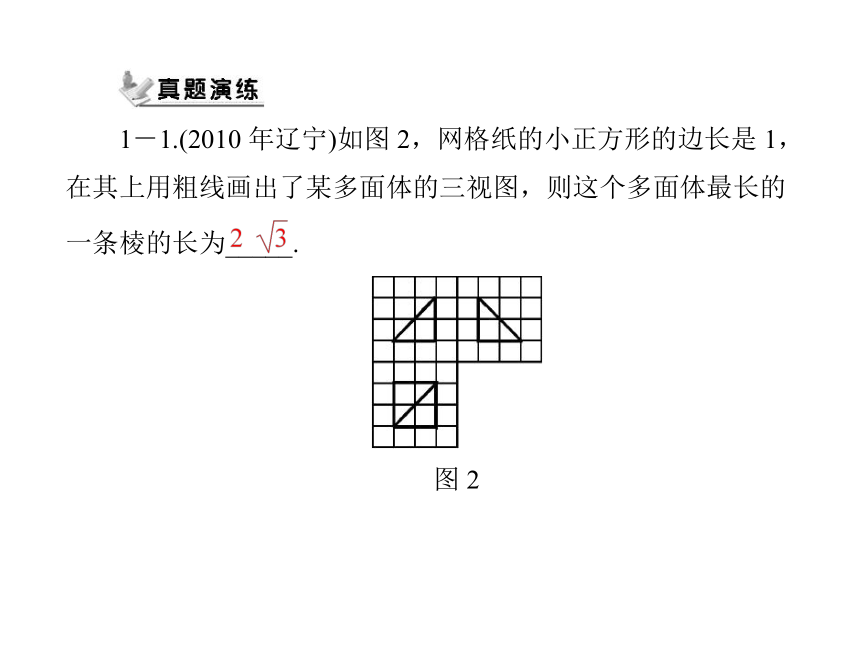
1-1.(2010 年辽宁)如图 2,网格纸的小正方形的边长是 1,
在其上用粗线画出了某多面体的三视图,则这个多面体最长的
一条棱的长为_____.
图 2
1-2.(2010 年福建)若一个底面是正三角形的三棱柱的正视
图如图 3,则其表面积等于__________.
解析:由正视图知:三棱柱是以底面边长为2,高为1 的正
图 3
专题二
几何体体积或表面积的相关计算
例 2:(2010 年上海)如图 4,为了制作一个圆柱形灯笼,先
要制作 4 个全等的矩形骨架,总计耗用 9.6 米铁丝,再用 S 平方
米塑料片制成圆柱的侧面和下底面(不安装上底面).
(1)当圆柱底面半径 r 取何值时,S 取得最大值?并求出该最
大值(结果精确到 0.01 平方米);
(2)若要制作一个如图 4 放置的,底面半径为 0.3 米的灯笼,
请作出用于灯笼的三视图(作图时,不需考虑骨架等因素).
图 4
解:(1)设圆柱形灯笼的母线长为 l,则 l=1.2-2r(0S=-3π(r-0.4)2+0.48π,
所以当 r=0.4 时,S 取得最大值约为 1.51 平方米.
(2)当 r=0.3 时,l=0.6,作三视图略.
2-1.(2010 年天津)一个几何体的三视图如图 5,则这个几
何体的体积为___.
3
图 5
2-2.(2010 年上海)已知四棱椎 P-ABCD 的底面是边长为 6
的正方形,侧棱 PA ⊥底面 ABCD,且 PA =8,则该四棱椎的体
积是___.
96
章末整合提升
专题一
三视图的应用
已知几何体的三视图,求该几何体的体积或表面积时,需
先由三视图还原出直观图,再根据直观图求几何体的体积或表
面积.
图 1
例 1:(2010 年天津)一个几何体的三视图如图 1,则这个几
何体的体积为________.
答案:
10
3
思维突破:由三视图可得,该几何体由一个正四棱柱和一
个正四棱锥组成,正四棱柱的底面边长为 1,高为 2,正四棱锥
的底面边长为 2 ,高为 1 ,故该几何体的体积 V =1×1×2 +
1-1.(2010 年辽宁)如图 2,网格纸的小正方形的边长是 1,
在其上用粗线画出了某多面体的三视图,则这个多面体最长的
一条棱的长为_____.
图 2
1-2.(2010 年福建)若一个底面是正三角形的三棱柱的正视
图如图 3,则其表面积等于__________.
解析:由正视图知:三棱柱是以底面边长为2,高为1 的正
图 3
专题二
几何体体积或表面积的相关计算
例 2:(2010 年上海)如图 4,为了制作一个圆柱形灯笼,先
要制作 4 个全等的矩形骨架,总计耗用 9.6 米铁丝,再用 S 平方
米塑料片制成圆柱的侧面和下底面(不安装上底面).
(1)当圆柱底面半径 r 取何值时,S 取得最大值?并求出该最
大值(结果精确到 0.01 平方米);
(2)若要制作一个如图 4 放置的,底面半径为 0.3 米的灯笼,
请作出用于灯笼的三视图(作图时,不需考虑骨架等因素).
图 4
解:(1)设圆柱形灯笼的母线长为 l,则 l=1.2-2r(0
所以当 r=0.4 时,S 取得最大值约为 1.51 平方米.
(2)当 r=0.3 时,l=0.6,作三视图略.
2-1.(2010 年天津)一个几何体的三视图如图 5,则这个几
何体的体积为___.
3
图 5
2-2.(2010 年上海)已知四棱椎 P-ABCD 的底面是边长为 6
的正方形,侧棱 PA ⊥底面 ABCD,且 PA =8,则该四棱椎的体
积是___.
96
