人教a版 必修二 第二章 2.1 2.1.2 空间中直线与直线之间的位置关系 配套课件
文档属性
| 名称 | 人教a版 必修二 第二章 2.1 2.1.2 空间中直线与直线之间的位置关系 配套课件 |  | |
| 格式 | rar | ||
| 文件大小 | 367.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-08-04 09:02:27 | ||
图片预览






文档简介
(共19张PPT)
2.1.2 空间中直线与直线之间的位置关系
1.给出下列四个命题,其中正确的是(
)
B
①在空间若两条直线不相交,则它们一定平行;
②平行于同一条直线的两条直线平行;
③一条直线和两条平行直线的一条相交,那么它也和另一
条相交;
④空间四条直线 a、b、c、d,如果 a∥b,c∥d,且 a∥d,
那么 b∥c.
A.①②③
B.②④
C.③④
D.②③
解析:①错,可以异面.②正确,公理 4.③错误,和另一
条可以异面.④正确,由平行直线的传递性可知.
2.空间两条互相平行的直线指的是(
)
D
A.在空间没有公共点的两条直线
B.分别在两个平面内的两条直线
C.在两个不同的平面内且没有公共点的两条直线.
D.在同一平面内且没有公共点的两条直线
3.若 a 和 b 是异面直线,b 和 c 是异面直线,则(
)
A.a∥c
D
B.a 和 c 是异面直线
C.a 和 c 相交
D.a 和 c 或平行或相交或异面
4.一条直线和两条异面直线中的一条相交,则它与另一条
的位置关系是(
)
D
A.平行
B.相交
C.异面
D.平行或相交或异面
重点
两直线的位置关系及公理 4
1.空间两条直线的位置关系:
2.公理 4:平行同一条直线的两条直线互相平行,它反映
了空间中的平行线也具有传递性.
3.等角定理:空间中如果两个角的两边分别平行,那么这
两个角相等或互补.
难点
两异面直线所成的角
已知两条异面直线 a、b,经过空间任一点 O 作直线 a′∥a,
b′∥b,把 a′、b′所成的锐角(或直角)叫异面直线 a、b 所成
的角(或夹角).a′、b′所成的角的大小与点 O 的选择无关,
为了简便,点 O 通常取在异面直线的一条上;异面直线所成的
角的范围为(0,90°],如果两条异面直线所成的角是直角,则叫
两条异面直线垂直,记作 a⊥b.求两条异面直线所成角的步骤可
以归纳为四步:选点→平移→定角→计算.
特别注意:如果已知条件中有中点,应首先考虑三角形的
中位线.
判断空间两直线的位置关系
例 1:下列说法正确的有(
)
①平行于同一直线的两条直线平行;
②垂直于同一直线的两条直线平行;
③过直线外一点,有且只有一条直线与已知直线平行;
④与已知直线平行且距离等于定长的直线只有两条.
A.1 个
C.3 个
B.2 个
D.4 个
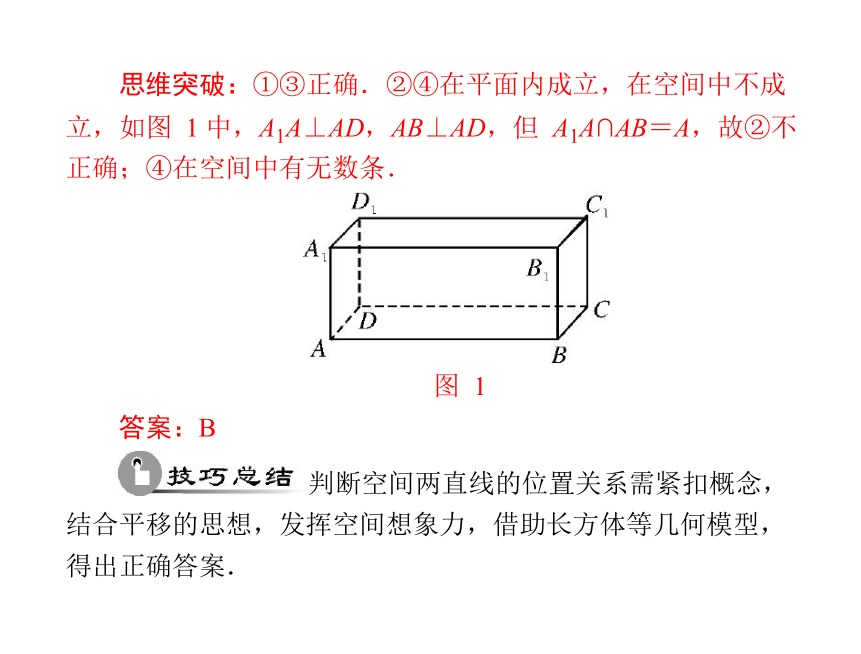
思维突破:①③正确.②④在平面内成立,在空间中不成
立,如图 1 中,A1A⊥AD,AB⊥AD,但 A1A∩AB=A,故②不
正确;④在空间中有无数条.
图 1
答案:B
判断空间两直线的位置关系需紧扣概念,
结合平移的思想,发挥空间想象力,借助长方体等几何模型,
得出正确答案.
1-1.在正方体 ABCD-A1B1C1D1 中,E、F 分别是 AA1、AB
的中点,试判断下列各对线段所在直线的位置关系:
(1)AB 与 CC1 _______;(2)A1B1 与 DC _____;
(3)A1C 与 D1B _____;(4)DC 与 BD1 ________;
(5)D1E 与 CF _____.
1-2.一条直线和两条异面直线中的一条平行,则它和另一
)
D
条的位置关系是(
A.平行
C.异面
B.相交
D.相交或异面
异面
平行
相交
异面
相交
平行公理的应用
例 2:空间四边形 ABCD 中,P、Q、R、H 分别是 AB、BC、
CD、DA 的中点.
(1)求证:四边形 PQRH 是平行四边形;
(2)若 AC=BD,则四边形 PQRH 是什么四边形?
(3)若 AC⊥BD,则四边形 PQRH 是什么四边形?
(4)空间四边形 ABCD 满足什么条件时,PQRH 是正方形?
解:(1)在△ABD 中,P、H 分别为 AB、AD 的中点,
即 PH 为中位线.
∴PH=PQ.
∴平行四边形 PQRH 为菱形.
(3)∵AC⊥BD,∴异面直线 AC 与 BD 所成角为直角.
∵PH∥BD,PQ∥AC,
∴∠HPQ 为 AC 与 BD 所成的角.
∴∠HPQ=90°,即四边形 PQRH 为矩形.
(4)由(2)、(3)的证明可知,当 AC=BD 且 AC⊥BD 时,四边
形 PQRH 为正方形.
2-1.如图 2,已知正方体 ABCD—A1B1C1D1,E、F、G、H
分别为 AB、AD、C1B1、C1D1 的中点,试判断下列直线是否平行.
图 2
(1)AD1 与 BC1;(2)EF 与 GH;(3)DE 与 HB1.
解:(1)平行.
∴ABC1D1 是平行四边形,∴AD1∥BC1.
(2)平行.
∵EF∥BD∥B1D1∥GH.
(3)平行.
取CD 中点为 S,连接 BS,可证 DE∥BS∥HB1.
求异面直线所成的角.
例 3:如图 3,在正方体 ABCD-A1B1C1D1 中.
图 3
(1)哪些棱所在的直线与直线 BA1 是异面直线?
(2)哪些棱所在的直线与直线 AA1 垂直?
(3)直线 BA1 和 CC1 的夹角是多少?
(4)直线 BA1 和 B1C 的夹角是多少?
(5)直线 BD 和 AC1 的夹角是多少?
解:(1)经过顶点 B、A1 的六条棱与直线 BA1 都相交,不是
异面直线,其余六条 CD、C1D1、CC1、DD1、C1B1、DA 与直线
BA1 都是异面直线.
(2)根据异面直线所成角的定义知,上底面、下底面的四条棱
都和直线 AA1 垂直,即 AB、BC、CD、DA、A1B1、B1C1、C1D1、
D1A1 所在的直线与直线 AA1 垂直.
(3)因为 CC1 ∥BB1,则∠B1BA 为直线 BA1 和 CC1 的夹角,
显然为 45°.
(4)连接 BD、A1D,因为 A1D ∥B1C,则∠BA1D 为直线 BA1
和 B1C 的夹角,又△ A1BD 是正三角形,所以∠BA1D=60°.
(5)分别取 B1B、D1D 的中点 E、F,连接 AE、EC1、C1F、
FA 、EF,显然 EF∥BD,四边形 AEC1F 为菱形,EF⊥AC1,即
BD⊥AC1,故直线 BD 和 AC1 的夹角是 90°.
求异面直线所成角的基本方法就是平移,
有时候平移两条直线,有时候只需要平移一条直线,得到两条
相交直线,最后在三角形或四边形中解决问题.
图 4
A.45°
B.60°
C.90°
D.120°
解析:连接 BC1、A1B、A1C1、EF,则 EF∥A1B,GH∥BC1,
∴∠A1BC1 是异面直线 EF、GH 所成的角,∵在正方体中,△ A1BC1
是等边三角形,∴∠A1BC1=60°.
B
所成的角等于(
)
3-1.如图 4,在正方体 ABCD-A1B1C1D1 中,E、F、G、
H 分别为 AA1、AB、BB1、B1C1 的中点,则异面直线 EF 与 GH
例 4:若 P 是两条异面直线 l、m 外的任意一点,则(
)
A.过点 P 有且仅有一条直线与 l、m 都平行
B.过点 P 有且仅有一条直线与 l、m 都垂直
C.过点 P 有且仅有一条直线与 l、m 都相交
D.过点 P 有且仅有一条直线与 l、m 都异面
正解:B
错因剖析:由公理 4 知过点 P 没有与 l、m 都平行的直线;
C、D 选项中,都有无数条直线.
4-1.(2010 年江西)如图 5,过正方体 ABCD-A1B1C1D1 的
顶点 A 作直线 l,使 l 与棱 AB、AD、AA1 所成的角都相等,这
样的直线 l 可以作(
)
图 5
A.1 条
B.2 条
C.3 条
D.4 条
解析:如图 13,将 A 移到 O 点,对应在 O 点建立坐标系,
形成 x 轴、y 轴、z 轴,l 与 x、y、z 轴所成角相等,这样的直线
刚好是 4 条体对角线所在直线,所以 4 条.
图 13
答案:D
2.1.2 空间中直线与直线之间的位置关系
1.给出下列四个命题,其中正确的是(
)
B
①在空间若两条直线不相交,则它们一定平行;
②平行于同一条直线的两条直线平行;
③一条直线和两条平行直线的一条相交,那么它也和另一
条相交;
④空间四条直线 a、b、c、d,如果 a∥b,c∥d,且 a∥d,
那么 b∥c.
A.①②③
B.②④
C.③④
D.②③
解析:①错,可以异面.②正确,公理 4.③错误,和另一
条可以异面.④正确,由平行直线的传递性可知.
2.空间两条互相平行的直线指的是(
)
D
A.在空间没有公共点的两条直线
B.分别在两个平面内的两条直线
C.在两个不同的平面内且没有公共点的两条直线.
D.在同一平面内且没有公共点的两条直线
3.若 a 和 b 是异面直线,b 和 c 是异面直线,则(
)
A.a∥c
D
B.a 和 c 是异面直线
C.a 和 c 相交
D.a 和 c 或平行或相交或异面
4.一条直线和两条异面直线中的一条相交,则它与另一条
的位置关系是(
)
D
A.平行
B.相交
C.异面
D.平行或相交或异面
重点
两直线的位置关系及公理 4
1.空间两条直线的位置关系:
2.公理 4:平行同一条直线的两条直线互相平行,它反映
了空间中的平行线也具有传递性.
3.等角定理:空间中如果两个角的两边分别平行,那么这
两个角相等或互补.
难点
两异面直线所成的角
已知两条异面直线 a、b,经过空间任一点 O 作直线 a′∥a,
b′∥b,把 a′、b′所成的锐角(或直角)叫异面直线 a、b 所成
的角(或夹角).a′、b′所成的角的大小与点 O 的选择无关,
为了简便,点 O 通常取在异面直线的一条上;异面直线所成的
角的范围为(0,90°],如果两条异面直线所成的角是直角,则叫
两条异面直线垂直,记作 a⊥b.求两条异面直线所成角的步骤可
以归纳为四步:选点→平移→定角→计算.
特别注意:如果已知条件中有中点,应首先考虑三角形的
中位线.
判断空间两直线的位置关系
例 1:下列说法正确的有(
)
①平行于同一直线的两条直线平行;
②垂直于同一直线的两条直线平行;
③过直线外一点,有且只有一条直线与已知直线平行;
④与已知直线平行且距离等于定长的直线只有两条.
A.1 个
C.3 个
B.2 个
D.4 个
思维突破:①③正确.②④在平面内成立,在空间中不成
立,如图 1 中,A1A⊥AD,AB⊥AD,但 A1A∩AB=A,故②不
正确;④在空间中有无数条.
图 1
答案:B
判断空间两直线的位置关系需紧扣概念,
结合平移的思想,发挥空间想象力,借助长方体等几何模型,
得出正确答案.
1-1.在正方体 ABCD-A1B1C1D1 中,E、F 分别是 AA1、AB
的中点,试判断下列各对线段所在直线的位置关系:
(1)AB 与 CC1 _______;(2)A1B1 与 DC _____;
(3)A1C 与 D1B _____;(4)DC 与 BD1 ________;
(5)D1E 与 CF _____.
1-2.一条直线和两条异面直线中的一条平行,则它和另一
)
D
条的位置关系是(
A.平行
C.异面
B.相交
D.相交或异面
异面
平行
相交
异面
相交
平行公理的应用
例 2:空间四边形 ABCD 中,P、Q、R、H 分别是 AB、BC、
CD、DA 的中点.
(1)求证:四边形 PQRH 是平行四边形;
(2)若 AC=BD,则四边形 PQRH 是什么四边形?
(3)若 AC⊥BD,则四边形 PQRH 是什么四边形?
(4)空间四边形 ABCD 满足什么条件时,PQRH 是正方形?
解:(1)在△ABD 中,P、H 分别为 AB、AD 的中点,
即 PH 为中位线.
∴PH=PQ.
∴平行四边形 PQRH 为菱形.
(3)∵AC⊥BD,∴异面直线 AC 与 BD 所成角为直角.
∵PH∥BD,PQ∥AC,
∴∠HPQ 为 AC 与 BD 所成的角.
∴∠HPQ=90°,即四边形 PQRH 为矩形.
(4)由(2)、(3)的证明可知,当 AC=BD 且 AC⊥BD 时,四边
形 PQRH 为正方形.
2-1.如图 2,已知正方体 ABCD—A1B1C1D1,E、F、G、H
分别为 AB、AD、C1B1、C1D1 的中点,试判断下列直线是否平行.
图 2
(1)AD1 与 BC1;(2)EF 与 GH;(3)DE 与 HB1.
解:(1)平行.
∴ABC1D1 是平行四边形,∴AD1∥BC1.
(2)平行.
∵EF∥BD∥B1D1∥GH.
(3)平行.
取CD 中点为 S,连接 BS,可证 DE∥BS∥HB1.
求异面直线所成的角.
例 3:如图 3,在正方体 ABCD-A1B1C1D1 中.
图 3
(1)哪些棱所在的直线与直线 BA1 是异面直线?
(2)哪些棱所在的直线与直线 AA1 垂直?
(3)直线 BA1 和 CC1 的夹角是多少?
(4)直线 BA1 和 B1C 的夹角是多少?
(5)直线 BD 和 AC1 的夹角是多少?
解:(1)经过顶点 B、A1 的六条棱与直线 BA1 都相交,不是
异面直线,其余六条 CD、C1D1、CC1、DD1、C1B1、DA 与直线
BA1 都是异面直线.
(2)根据异面直线所成角的定义知,上底面、下底面的四条棱
都和直线 AA1 垂直,即 AB、BC、CD、DA、A1B1、B1C1、C1D1、
D1A1 所在的直线与直线 AA1 垂直.
(3)因为 CC1 ∥BB1,则∠B1BA 为直线 BA1 和 CC1 的夹角,
显然为 45°.
(4)连接 BD、A1D,因为 A1D ∥B1C,则∠BA1D 为直线 BA1
和 B1C 的夹角,又△ A1BD 是正三角形,所以∠BA1D=60°.
(5)分别取 B1B、D1D 的中点 E、F,连接 AE、EC1、C1F、
FA 、EF,显然 EF∥BD,四边形 AEC1F 为菱形,EF⊥AC1,即
BD⊥AC1,故直线 BD 和 AC1 的夹角是 90°.
求异面直线所成角的基本方法就是平移,
有时候平移两条直线,有时候只需要平移一条直线,得到两条
相交直线,最后在三角形或四边形中解决问题.
图 4
A.45°
B.60°
C.90°
D.120°
解析:连接 BC1、A1B、A1C1、EF,则 EF∥A1B,GH∥BC1,
∴∠A1BC1 是异面直线 EF、GH 所成的角,∵在正方体中,△ A1BC1
是等边三角形,∴∠A1BC1=60°.
B
所成的角等于(
)
3-1.如图 4,在正方体 ABCD-A1B1C1D1 中,E、F、G、
H 分别为 AA1、AB、BB1、B1C1 的中点,则异面直线 EF 与 GH
例 4:若 P 是两条异面直线 l、m 外的任意一点,则(
)
A.过点 P 有且仅有一条直线与 l、m 都平行
B.过点 P 有且仅有一条直线与 l、m 都垂直
C.过点 P 有且仅有一条直线与 l、m 都相交
D.过点 P 有且仅有一条直线与 l、m 都异面
正解:B
错因剖析:由公理 4 知过点 P 没有与 l、m 都平行的直线;
C、D 选项中,都有无数条直线.
4-1.(2010 年江西)如图 5,过正方体 ABCD-A1B1C1D1 的
顶点 A 作直线 l,使 l 与棱 AB、AD、AA1 所成的角都相等,这
样的直线 l 可以作(
)
图 5
A.1 条
B.2 条
C.3 条
D.4 条
解析:如图 13,将 A 移到 O 点,对应在 O 点建立坐标系,
形成 x 轴、y 轴、z 轴,l 与 x、y、z 轴所成角相等,这样的直线
刚好是 4 条体对角线所在直线,所以 4 条.
图 13
答案:D
