人教a版 必修二 第二章 2.2 2.2.3 平面与平面平行的性质 配套课件
文档属性
| 名称 | 人教a版 必修二 第二章 2.2 2.2.3 平面与平面平行的性质 配套课件 |  | |
| 格式 | rar | ||
| 文件大小 | 443.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-08-04 09:02:27 | ||
图片预览






文档简介
(共18张PPT)
2.2.3 平面与平面平行的性质
1.下列四个命题中,假命题是(
)
C
A.如果平面α内有两相交直线与平面β内的两条相交直线对
应平行,则α∥β
B.平行于同一平面的两个平面平行
C.如果平面α内有无数条直线都与平面β平行,则α∥β
D.如果平面α内任意一条直线都与平面β平行,则α∥β
2.若平面α∥平面β,直线 a α,点 B∈β,则在β内过点 B
的所有直线中(
)
D
A.不一定存在与 a 平行的直线
B.只有两条与 a 平行的直线
C.存在无数多条与 a 平行的直线
D.存在唯一一条与 a 平行的直线
3.下列命题中,真命题的个数是(
)
D
①如果两个平面平行,那么其中一个平面内的直线平行于
另一个平面;②如果两个平面平行,那么其中一个平面内的直
线与另一个平面没有公共点;③两个平面平行等价于一个平面
内的任意一条直线与另一个平面没有公共点.
A.0 个
B.1 个
C.2 个
D.3 个
4.下列命题中,真命题的个数是(
)
C
①如果两个平面平行,那么分别在两个平面内存在直线 a、
b,使 a∥b;②如果两个平行平面同时和第三个平面相交,那么
它们的交线平行;③如果两个平面平行,那么第一个平面内的
直线与第二个平面内的直线平行.
B.1 个
D.3 个
A.0 个
C.2 个
解析:①、②真,③假.
重点
面面平行的性质定理
1.面面平行的性质(1):如果两个平行平面同时与第三个平
面相交,那么它们的交线平行.用符号语言表示为:α∥β,γ∩
α =a,γ∩β=b a∥b.如图 1.
图 1
2.面面平行的性质(2):α∥β,l α l∥β.
特别注意:本定理既是面面平行的性质定理,也是线面平
行的判定定理,因此证明线面平行,也可借助于面面平行.
难点
面面平行的判定及性质中的关系转换
利用两个平行平面的性质解题时,要注意常把面面平行的
问题转化成线面平行或线线平行的问题.
(1)两个平面平行,可得其中一平面内的任一直线平行于另
一个平面,此性质定理可简记为:面面平行,则线面平行;
(2)两个平面平行,可得两个平面与第三个平面相交,它们
的交线平行,而不是两个平面内的任意两条直线平行,此性质
定理可简记为:面面平行,则线线平行.
面面平行的性质定理的应用
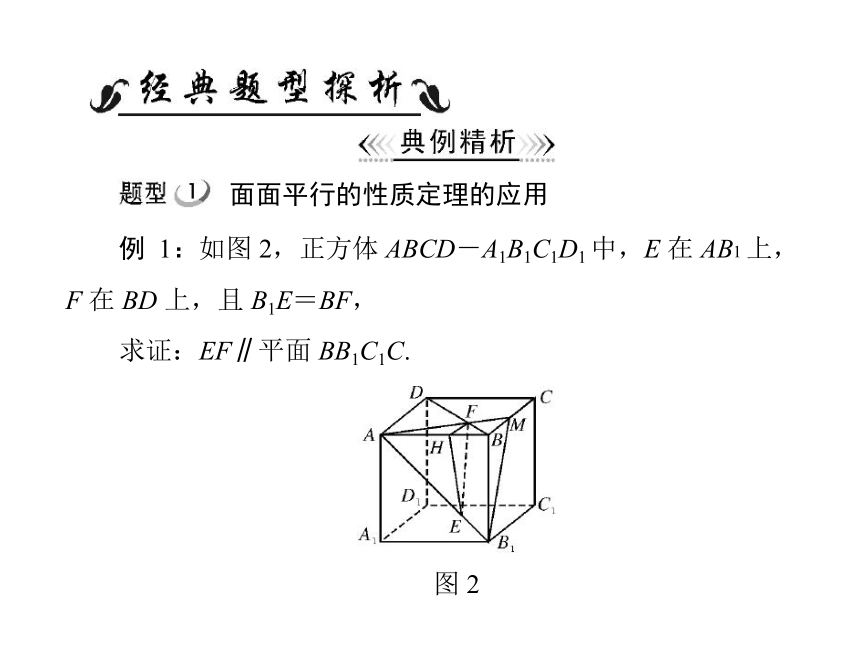
例 1:如图 2,正方体 ABCD-A1B1C1D1 中,E 在 AB1 上,
F 在 BD 上,且 B1E=BF,
求证:EF∥平面 BB1C1C.
图 2
=
=
证法一:连接 AF 并延长交 BC 于 M,连接 B1M,
∵AD∥BC,∴ AFD∽MFB,
∴
AF
FM
DF
BF
.
又∵BD=B1A,B1E=BF,∴DF=AE.
∴
AF AE
FM B1E
,∴EF∥B1M,B1M 平面 BB1C1C.
∴EF∥平面 BB1C1C.
证法二:作 FH∥AD 交 AB 于 H,连接 HE.
∵AD∥BC,∴FH∥BC,BC BB1C1C.
=
∴FH∥平面 BB1C1C.
由 FH∥AD 可得
BF
BD
BH
.
BA
∴EH∥B1B,B1B 平面 BB1C1C.
∴EH∥平面 BB1C1C,EH∩FH=H.
∴平面 FHE∥平面 BB1C1C,EF 平面 FHE.
∴EF∥平面 BB1C1C.
证法一为了证线面平行,先证线线平行.证
法二则是证线面平行,先证面面平行,然后说明直线在其中一
个平面内.
1-1.已知平面α∥平面β,P 是α、β外一点,过 P 点的两条
直线分别交α于 A、B,交β于 C、D,且 PA =6,AC=9,AB=8,
则 CD 的长为_______.
20 或 4
图 3
证明:连接 BC.
取 BC 的中点 E,分别连接 ME、NE,则 ME∥AC,
∴ME∥α.
同理:NE∥BD,∴NE∥β.
又 ME∩NE=E,
∴平面 MEN∥平面α.
∵MN 平面 MEN,
∴MN∥α.
面面平行的判定定理与性质定理的综合应用
例 2:如图 3,设平面α∥平面β,AB、CD 是两异面直线,
M、N 分别是 AB、CD 的中点,且 A、C∈α,B、D∈β.求证:
MN∥α.
将空间问题转化为平面问题,是解决立体
几何问题的重要策略,关键在于选择或添加适当的平面或线,
并抓住一些平面图形的几何性质,如比例线段等.此题通过巧
作辅助线,得到所作平面与底面平行,由性质α ∥β,l α
l∥β易得线面平行,进而转化为面面平行,突出了平行问题中
的转化思想.
图 4
证明:如图20,作EP⊥BB1 于P,连接PF.在正三棱柱
ABC -A1B1C1 的侧面 ABB1A1 中,易知 A1B1⊥BB1,
2-1.如图 4,在正三棱柱 ABC-A1B1C1 中,E、F、G 是侧
面对角线上的点,且 BE=CF=AG.
求证:平面 EFG∥平面 ABC.
图 20
=
又EP⊥BB1,∴EP∥A1B1∥AB.
∴EP∥平面 ABC,且
BE BP
.
A1B BB1
∴PF∥BC,则 PF∥平面 ABC.
∵EP∩PF=P,∴平面 PEF∥平面 ABC.
∵EF 平面 PEF,∴EF∥平面 ABC.
同理:GF∥平面 ABC.
∵EF∩GF=F,∴平面 EFG∥平面 ABC.
利用面面平行证线面平行
例 3:已知:有公共边 AB 的两个正方形 ABCD 和 ABEF 不
在同一平面内,P、Q 分别是对角线 AE、BD 上的点,且 AP=
DQ,求证:PQ∥平面 CBE.
=
证法一:如图 (1),连接AQ 并延长交BC 于G,
连接EG,则
AQ
QG
DQ
.
QB
∵AP=DQ, PE=BQ,
∴
AQ
QG
=
AP
PE
.
∴
PQ
∥
EG
,
又
PQ
平面
BCE
,
EG
面
BCE
,
∴
PQ
∥
面
BCE
.
证法二:
如图
(2)
,分别过
P
、
Q
作
PK
∥
AB
,
QH
∥
AB
,则
PK
∥
QH
,
连接
KH
,则
PK
AB
=
PE
AE
,
QH
CD
=
BQ
BD
.
∵
CD
=
AB
,
AE
=
BD
,
PE
=
BQ
,
∴
PK
=
QH
,
∴PQHK 是平行四边形.∴PQ∥KH,
又 PQ 平面 BCE,KH 面 BCE,
∴PQ∥面 BCE.
证法三:如图 (3),过 P 作 PO∥EB,连接 OQ,
则 OQ∥AD∥BC,面 POQ∥面 BEC,
又 PQ 平面 BCE,故 PQ∥面 BEC.
证明线面平行,关键是在平面内找到一条直
线与已知直线平行,证法一是作三角形得到的;证法二是通过
作平行四边形得到在平面内的一条直线 KH;证法三利用了面面
平行的性质定理.
证法一:如图21,连接 EF、AC,AC∩BD=G,
图 21
显然四边形 EFAG 为平行四边形,
又AF 平面 BDE,EG 平面 BDE ,∴AF∥平面BDE.
证法二:取A1B1 中点G,连接AG、FG,证明平面AFG∥
平面BDE 即可.
3-1.如图 6,在长方体 ABCD-A1B1C1D1 中,点 E、F 是棱
C1D1、A1D1 的中点,求证:AF∥平面 BDE.
图 6
例 4:下列命题正确的是(
)
A.夹在两平行平面间的平行线段相等
B.夹在两平行平面间的相等线段必平行
C.两平面分别与第三平面相交,若两条交线平行,则这两
平面平行
D.平行于同一直线的两平面平行
正解:A
错因剖析:没有注意面面平行性质定理的应用条件.
2.2.3 平面与平面平行的性质
1.下列四个命题中,假命题是(
)
C
A.如果平面α内有两相交直线与平面β内的两条相交直线对
应平行,则α∥β
B.平行于同一平面的两个平面平行
C.如果平面α内有无数条直线都与平面β平行,则α∥β
D.如果平面α内任意一条直线都与平面β平行,则α∥β
2.若平面α∥平面β,直线 a α,点 B∈β,则在β内过点 B
的所有直线中(
)
D
A.不一定存在与 a 平行的直线
B.只有两条与 a 平行的直线
C.存在无数多条与 a 平行的直线
D.存在唯一一条与 a 平行的直线
3.下列命题中,真命题的个数是(
)
D
①如果两个平面平行,那么其中一个平面内的直线平行于
另一个平面;②如果两个平面平行,那么其中一个平面内的直
线与另一个平面没有公共点;③两个平面平行等价于一个平面
内的任意一条直线与另一个平面没有公共点.
A.0 个
B.1 个
C.2 个
D.3 个
4.下列命题中,真命题的个数是(
)
C
①如果两个平面平行,那么分别在两个平面内存在直线 a、
b,使 a∥b;②如果两个平行平面同时和第三个平面相交,那么
它们的交线平行;③如果两个平面平行,那么第一个平面内的
直线与第二个平面内的直线平行.
B.1 个
D.3 个
A.0 个
C.2 个
解析:①、②真,③假.
重点
面面平行的性质定理
1.面面平行的性质(1):如果两个平行平面同时与第三个平
面相交,那么它们的交线平行.用符号语言表示为:α∥β,γ∩
α =a,γ∩β=b a∥b.如图 1.
图 1
2.面面平行的性质(2):α∥β,l α l∥β.
特别注意:本定理既是面面平行的性质定理,也是线面平
行的判定定理,因此证明线面平行,也可借助于面面平行.
难点
面面平行的判定及性质中的关系转换
利用两个平行平面的性质解题时,要注意常把面面平行的
问题转化成线面平行或线线平行的问题.
(1)两个平面平行,可得其中一平面内的任一直线平行于另
一个平面,此性质定理可简记为:面面平行,则线面平行;
(2)两个平面平行,可得两个平面与第三个平面相交,它们
的交线平行,而不是两个平面内的任意两条直线平行,此性质
定理可简记为:面面平行,则线线平行.
面面平行的性质定理的应用
例 1:如图 2,正方体 ABCD-A1B1C1D1 中,E 在 AB1 上,
F 在 BD 上,且 B1E=BF,
求证:EF∥平面 BB1C1C.
图 2
=
=
证法一:连接 AF 并延长交 BC 于 M,连接 B1M,
∵AD∥BC,∴ AFD∽MFB,
∴
AF
FM
DF
BF
.
又∵BD=B1A,B1E=BF,∴DF=AE.
∴
AF AE
FM B1E
,∴EF∥B1M,B1M 平面 BB1C1C.
∴EF∥平面 BB1C1C.
证法二:作 FH∥AD 交 AB 于 H,连接 HE.
∵AD∥BC,∴FH∥BC,BC BB1C1C.
=
∴FH∥平面 BB1C1C.
由 FH∥AD 可得
BF
BD
BH
.
BA
∴EH∥B1B,B1B 平面 BB1C1C.
∴EH∥平面 BB1C1C,EH∩FH=H.
∴平面 FHE∥平面 BB1C1C,EF 平面 FHE.
∴EF∥平面 BB1C1C.
证法一为了证线面平行,先证线线平行.证
法二则是证线面平行,先证面面平行,然后说明直线在其中一
个平面内.
1-1.已知平面α∥平面β,P 是α、β外一点,过 P 点的两条
直线分别交α于 A、B,交β于 C、D,且 PA =6,AC=9,AB=8,
则 CD 的长为_______.
20 或 4
图 3
证明:连接 BC.
取 BC 的中点 E,分别连接 ME、NE,则 ME∥AC,
∴ME∥α.
同理:NE∥BD,∴NE∥β.
又 ME∩NE=E,
∴平面 MEN∥平面α.
∵MN 平面 MEN,
∴MN∥α.
面面平行的判定定理与性质定理的综合应用
例 2:如图 3,设平面α∥平面β,AB、CD 是两异面直线,
M、N 分别是 AB、CD 的中点,且 A、C∈α,B、D∈β.求证:
MN∥α.
将空间问题转化为平面问题,是解决立体
几何问题的重要策略,关键在于选择或添加适当的平面或线,
并抓住一些平面图形的几何性质,如比例线段等.此题通过巧
作辅助线,得到所作平面与底面平行,由性质α ∥β,l α
l∥β易得线面平行,进而转化为面面平行,突出了平行问题中
的转化思想.
图 4
证明:如图20,作EP⊥BB1 于P,连接PF.在正三棱柱
ABC -A1B1C1 的侧面 ABB1A1 中,易知 A1B1⊥BB1,
2-1.如图 4,在正三棱柱 ABC-A1B1C1 中,E、F、G 是侧
面对角线上的点,且 BE=CF=AG.
求证:平面 EFG∥平面 ABC.
图 20
=
又EP⊥BB1,∴EP∥A1B1∥AB.
∴EP∥平面 ABC,且
BE BP
.
A1B BB1
∴PF∥BC,则 PF∥平面 ABC.
∵EP∩PF=P,∴平面 PEF∥平面 ABC.
∵EF 平面 PEF,∴EF∥平面 ABC.
同理:GF∥平面 ABC.
∵EF∩GF=F,∴平面 EFG∥平面 ABC.
利用面面平行证线面平行
例 3:已知:有公共边 AB 的两个正方形 ABCD 和 ABEF 不
在同一平面内,P、Q 分别是对角线 AE、BD 上的点,且 AP=
DQ,求证:PQ∥平面 CBE.
=
证法一:如图 (1),连接AQ 并延长交BC 于G,
连接EG,则
AQ
QG
DQ
.
QB
∵AP=DQ, PE=BQ,
∴
AQ
QG
=
AP
PE
.
∴
PQ
∥
EG
,
又
PQ
平面
BCE
,
EG
面
BCE
,
∴
PQ
∥
面
BCE
.
证法二:
如图
(2)
,分别过
P
、
Q
作
PK
∥
AB
,
QH
∥
AB
,则
PK
∥
QH
,
连接
KH
,则
PK
AB
=
PE
AE
,
QH
CD
=
BQ
BD
.
∵
CD
=
AB
,
AE
=
BD
,
PE
=
BQ
,
∴
PK
=
QH
,
∴PQHK 是平行四边形.∴PQ∥KH,
又 PQ 平面 BCE,KH 面 BCE,
∴PQ∥面 BCE.
证法三:如图 (3),过 P 作 PO∥EB,连接 OQ,
则 OQ∥AD∥BC,面 POQ∥面 BEC,
又 PQ 平面 BCE,故 PQ∥面 BEC.
证明线面平行,关键是在平面内找到一条直
线与已知直线平行,证法一是作三角形得到的;证法二是通过
作平行四边形得到在平面内的一条直线 KH;证法三利用了面面
平行的性质定理.
证法一:如图21,连接 EF、AC,AC∩BD=G,
图 21
显然四边形 EFAG 为平行四边形,
又AF 平面 BDE,EG 平面 BDE ,∴AF∥平面BDE.
证法二:取A1B1 中点G,连接AG、FG,证明平面AFG∥
平面BDE 即可.
3-1.如图 6,在长方体 ABCD-A1B1C1D1 中,点 E、F 是棱
C1D1、A1D1 的中点,求证:AF∥平面 BDE.
图 6
例 4:下列命题正确的是(
)
A.夹在两平行平面间的平行线段相等
B.夹在两平行平面间的相等线段必平行
C.两平面分别与第三平面相交,若两条交线平行,则这两
平面平行
D.平行于同一直线的两平面平行
正解:A
错因剖析:没有注意面面平行性质定理的应用条件.
