人教版数学八年级上册11.3.1 多边形的有关概念课件(共24张PPT)
文档属性
| 名称 | 人教版数学八年级上册11.3.1 多边形的有关概念课件(共24张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-23 00:00:00 | ||
图片预览



文档简介
多边形的有关概念
学习目标
多边形的定义及相关概念.
推导多边形对角条数的计算公式.
多边形的分类.
知识精讲
你能从图中想象出几个由一些线段围成的图形吗?
知识精讲
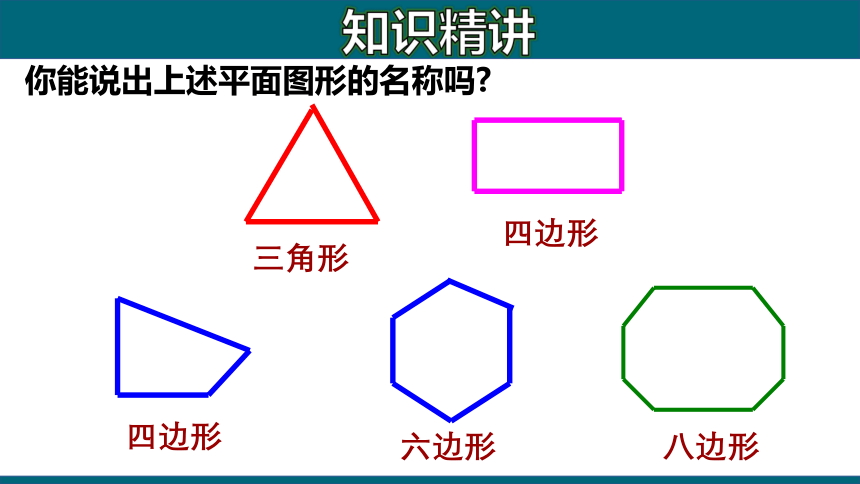
你能说出上述平面图形的名称吗?
三角形
四边形
四边形
六边形
八边形
知识精讲
什么叫三角形?
由不在同一条直线上的三条线段首尾顺次相接所组成的图形叫做三角形。
什么叫多边形?
在平面内,由一些线段首尾顺次相接组成的封闭图形叫做多边形。
多边形的概念
知识精讲
在多边形的概念中,要分清以下几个方面:
(1)在平面内;
(2)若干线段不在同一直线上;
(3)首尾顺次相接;
(4)所形成的是封闭图形.
知识精讲
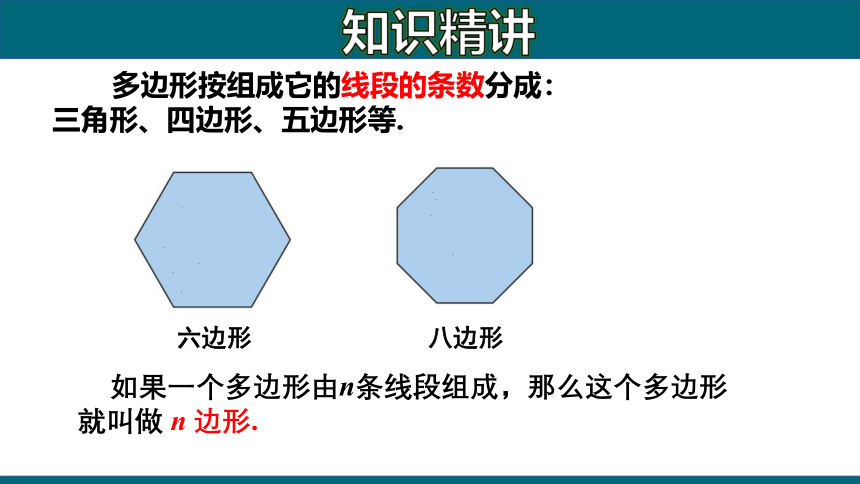
六边形
八边形
如果一个多边形由n条线段组成,那么这个多边形就叫做 n 边形.
多边形按组成它的线段的条数分成:
三角形、四边形、五边形等.
知识精讲
A
B
C
D
E
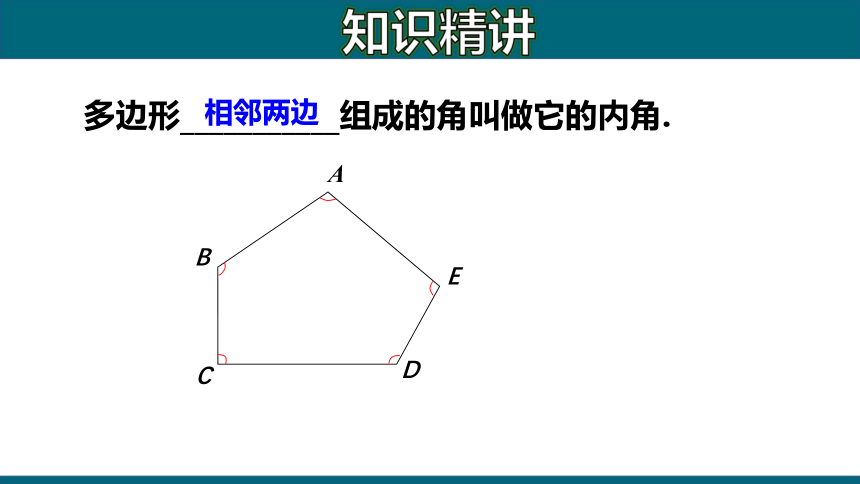
多边形___________组成的角叫做它的内角.
相邻两边
知识精讲
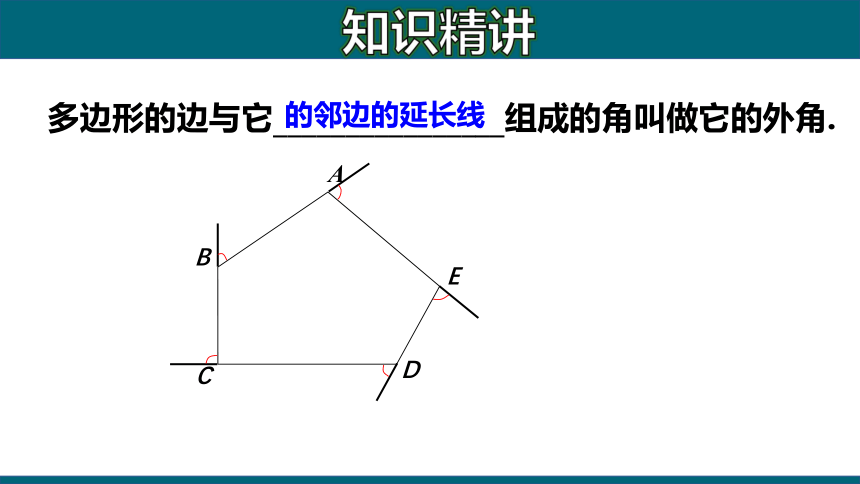
多边形的边与它________________组成的角叫做它的外角.
的邻边的延长线
A
B
C
D
E
巩固训练
1.下列图形包含了哪些多边形?
六边形
四边形
五边形和
六边形
知识精讲
A
B
C
D
E
如图,从五边形ABCDE 的顶点A 出发共有几条对角线?
连接多边形不相邻的两个顶点的线段,叫做多边形的对角线。
共有AC,AD2条对角线
三角形是最简单的多边形,研究多边形可借助对角线将其分为若干个三角形。
知识精讲
{5A111915-BE36-4E01-A7E5-04B1672EAD32}边数
图形
从多边形的一个顶点引出的对角线条数
三角形
四边形
五边形
六边形
……
n 边形
······
0
3 - 3=
4 - 3=
5 - 3 =
6 - 3 =
n - 3
1
2
3
······
探索
边数
3
4
5
6
7
…
n
从一个顶点出发的对角线的条数
上述对角线分成的三角形个数
…
总的对角线条数
…
0
1
0
1
2
2
2
3
5
3
4
9
4
5
14
n-3
n-2
n(n-3)
2
凸n边形对
角线条数:
n(n-3)
2
知识精讲
2. (1)四边形的一条对角线将四边形分成几个三角形?
(2)从五边形的一个顶点出发,可以画出几条对角线?
它们将五边形分成了几个三角形?
2 个三角形
2条对角线
3个三角形
3.画出下图多边形的全部对角线.
知识精讲
(1)
(2)
凸四边形
凹四边形
观察 你能说出这两幅图形的异同点吗?
知识精讲
A
B
C
D
A
B
C
D
图1
图2
如图2,多边形ABCD不在CD所在直线的同侧,就不是凸多边形,叫凹多边形.
如图1,画出任意一边所在的直线,整个多边形都在直线的同侧,这样的多边形叫做凸多边形.
没有特别说明,我们研究的多边形都是指凸多边形.
多边形的分类
知识精讲
2.下图中,你能找到哪些多边形?哪些是凸多边形,哪些是凹多边形?
巩固训练
观察图中的多边形,它们的边、角有什么特点?
正三角形
正方形
正五边形
正六边形
正八边形
在平面内,各个角都相等、各条边都相等的多边形叫做正多边形。
知识精讲
当n>3时,必须同时满足以下两个条件:
(1)是各边相等,
(2)是各角相等。
两者缺一不可.
如长方形各角相等,但各边不一定相等;菱形各边相等,但各角不一定相等.所以它们都不是正多边形。
菱形
矩形
正三角形
正方形
判断一个n边形是正n边形的条件
知识精讲
巩固训练
1.六边形的对角线共有( )
A.6条 B.7条 C.8条 D.9条
2.下列属于正多边形的是( )
A.长方形 B.等边三角形
C.梯形 D.圆
D
B
基础巩固
3.从一个顶点出发的对角线,可以把十边形分成互不重叠的三角形的个数( )
A.7个 B.8个 C.9个 D.10个
4.十二边形共有_____条对角线,过一个顶点可作_____条对角线,可把十二边形分成_____个三角形.
B
54
9
10
巩固训练
5.已知一个多边形有35条对角线,你能求出它的边数吗?
6.有一个家庭联谊会,参加的家庭全部是三口之家,在联谊会期间,每个人都要和别的家庭的每个成员握一次手。
(1)若参加会议的人数为15,则一共要握手多少次?
(2)若一共握手170次,则参加会议的人数是多少?
n(n-3)
2
=35
n=10
(1)
=90;
15 (15-3)
2
×
( 2 )
n(n-3)
2
=170
n=20
巩固训练
小结梳理
1.多边形的定义
在平面内,由一些线段首尾顺次相接组成的图形。
2.多边形的内角
多边形相邻两边组成的角。
3.多边形的外角
多边形的一边与它相邻边的延长线组成的角。
4.多边形的对角线
连接多边形不相邻的两个顶点的线段。
5.正多边形
各个角相等,各条边都相等的多边形。
学习目标
多边形的定义及相关概念.
推导多边形对角条数的计算公式.
多边形的分类.
知识精讲
你能从图中想象出几个由一些线段围成的图形吗?
知识精讲
你能说出上述平面图形的名称吗?
三角形
四边形
四边形
六边形
八边形
知识精讲
什么叫三角形?
由不在同一条直线上的三条线段首尾顺次相接所组成的图形叫做三角形。
什么叫多边形?
在平面内,由一些线段首尾顺次相接组成的封闭图形叫做多边形。
多边形的概念
知识精讲
在多边形的概念中,要分清以下几个方面:
(1)在平面内;
(2)若干线段不在同一直线上;
(3)首尾顺次相接;
(4)所形成的是封闭图形.
知识精讲
六边形
八边形
如果一个多边形由n条线段组成,那么这个多边形就叫做 n 边形.
多边形按组成它的线段的条数分成:
三角形、四边形、五边形等.
知识精讲
A
B
C
D
E
多边形___________组成的角叫做它的内角.
相邻两边
知识精讲
多边形的边与它________________组成的角叫做它的外角.
的邻边的延长线
A
B
C
D
E
巩固训练
1.下列图形包含了哪些多边形?
六边形
四边形
五边形和
六边形
知识精讲
A
B
C
D
E
如图,从五边形ABCDE 的顶点A 出发共有几条对角线?
连接多边形不相邻的两个顶点的线段,叫做多边形的对角线。
共有AC,AD2条对角线
三角形是最简单的多边形,研究多边形可借助对角线将其分为若干个三角形。
知识精讲
{5A111915-BE36-4E01-A7E5-04B1672EAD32}边数
图形
从多边形的一个顶点引出的对角线条数
三角形
四边形
五边形
六边形
……
n 边形
······
0
3 - 3=
4 - 3=
5 - 3 =
6 - 3 =
n - 3
1
2
3
······
探索
边数
3
4
5
6
7
…
n
从一个顶点出发的对角线的条数
上述对角线分成的三角形个数
…
总的对角线条数
…
0
1
0
1
2
2
2
3
5
3
4
9
4
5
14
n-3
n-2
n(n-3)
2
凸n边形对
角线条数:
n(n-3)
2
知识精讲
2. (1)四边形的一条对角线将四边形分成几个三角形?
(2)从五边形的一个顶点出发,可以画出几条对角线?
它们将五边形分成了几个三角形?
2 个三角形
2条对角线
3个三角形
3.画出下图多边形的全部对角线.
知识精讲
(1)
(2)
凸四边形
凹四边形
观察 你能说出这两幅图形的异同点吗?
知识精讲
A
B
C
D
A
B
C
D
图1
图2
如图2,多边形ABCD不在CD所在直线的同侧,就不是凸多边形,叫凹多边形.
如图1,画出任意一边所在的直线,整个多边形都在直线的同侧,这样的多边形叫做凸多边形.
没有特别说明,我们研究的多边形都是指凸多边形.
多边形的分类
知识精讲
2.下图中,你能找到哪些多边形?哪些是凸多边形,哪些是凹多边形?
巩固训练
观察图中的多边形,它们的边、角有什么特点?
正三角形
正方形
正五边形
正六边形
正八边形
在平面内,各个角都相等、各条边都相等的多边形叫做正多边形。
知识精讲
当n>3时,必须同时满足以下两个条件:
(1)是各边相等,
(2)是各角相等。
两者缺一不可.
如长方形各角相等,但各边不一定相等;菱形各边相等,但各角不一定相等.所以它们都不是正多边形。
菱形
矩形
正三角形
正方形
判断一个n边形是正n边形的条件
知识精讲
巩固训练
1.六边形的对角线共有( )
A.6条 B.7条 C.8条 D.9条
2.下列属于正多边形的是( )
A.长方形 B.等边三角形
C.梯形 D.圆
D
B
基础巩固
3.从一个顶点出发的对角线,可以把十边形分成互不重叠的三角形的个数( )
A.7个 B.8个 C.9个 D.10个
4.十二边形共有_____条对角线,过一个顶点可作_____条对角线,可把十二边形分成_____个三角形.
B
54
9
10
巩固训练
5.已知一个多边形有35条对角线,你能求出它的边数吗?
6.有一个家庭联谊会,参加的家庭全部是三口之家,在联谊会期间,每个人都要和别的家庭的每个成员握一次手。
(1)若参加会议的人数为15,则一共要握手多少次?
(2)若一共握手170次,则参加会议的人数是多少?
n(n-3)
2
=35
n=10
(1)
=90;
15 (15-3)
2
×
( 2 )
n(n-3)
2
=170
n=20
巩固训练
小结梳理
1.多边形的定义
在平面内,由一些线段首尾顺次相接组成的图形。
2.多边形的内角
多边形相邻两边组成的角。
3.多边形的外角
多边形的一边与它相邻边的延长线组成的角。
4.多边形的对角线
连接多边形不相邻的两个顶点的线段。
5.正多边形
各个角相等,各条边都相等的多边形。
