人教版数学八年级上册11.3.2 多边形的外角和课件(共20张PPT)
文档属性
| 名称 | 人教版数学八年级上册11.3.2 多边形的外角和课件(共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-23 00:00:00 | ||
图片预览






文档简介
多边形的外角和
学习目标
能利用外角和公式解决问题.
探索并求出多边形外角和.
情境引入
跑步可以强身健体,提高抵抗力。小赵沿一个六边形花坛,按逆时针方向跑步,每跑一圈回到原点,需要转过多少的角度?他都转过哪些角?
知识精讲
(1)小赵每从一条小路转到下一条小路时,跑步方向改变的角是哪个角?
分别是∠1,∠2,∠3,∠4,∠5,∠6
(2)求“他每跑一圈回到原点,需要转过多少的角度”,实际上是求什么?
∠1+∠2+∠3+∠4+∠5+∠6
思考
知识精讲
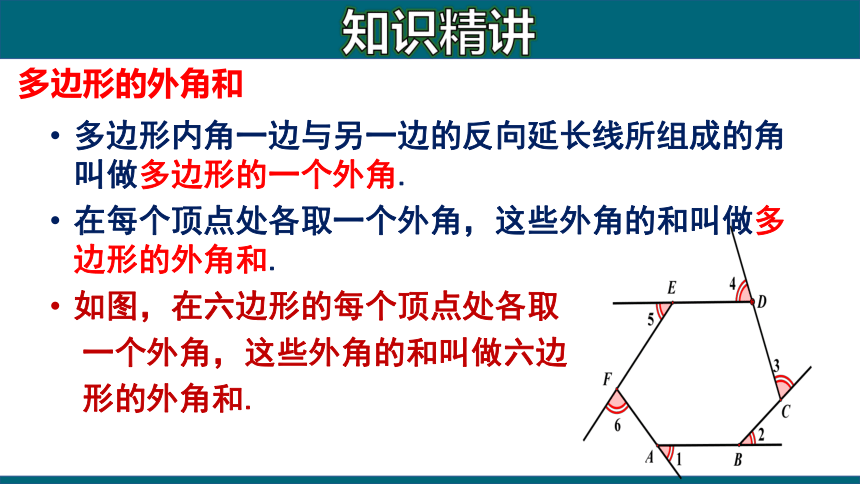
多边形内角一边与另一边的反向延长线所组成的角叫做多边形的一个外角.
在每个顶点处各取一个外角,这些外角的和叫做多边形的外角和.
如图,在六边形的每个顶点处各取
一个外角,这些外角的和叫做六边
形的外角和.
多边形的外角和
知识链接
1、n边形的内角和公式是什么?
(n-2)×180°
2、三角形的外角和是多少?你还记得这个结论是如何得出的吗?
360°
知识精讲
问题1:任意一个外角和它相邻的内角有什么关系?
互补
即 ∠1+∠FAB=180°,∠2+∠ABC=180°,
∠3+∠BCD=180°,∠4+∠CDE=180°,
∠5+∠DEF=180°,∠6+∠EFA=180°
六边形的外角和
知识精讲
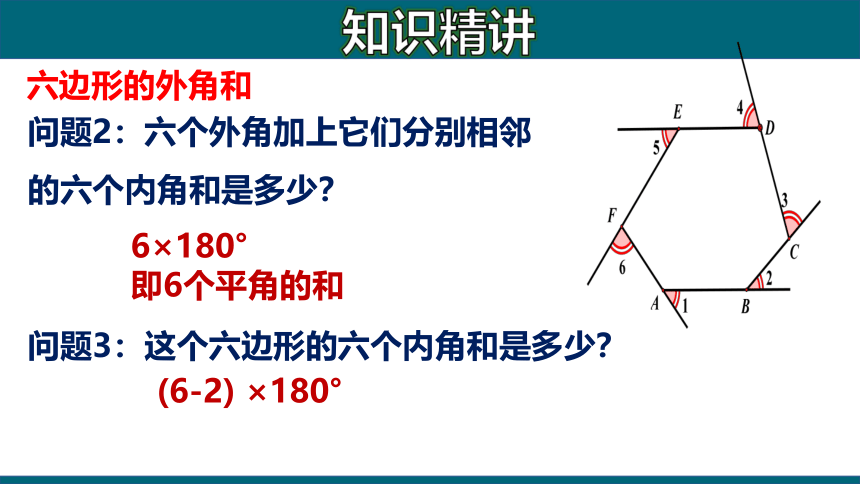
问题2:六个外角加上它们分别相邻的六个内角和是多少?
6×180°
即6个平角的和
问题3:这个六边形的六个内角和是多少?
(6-2) ×180°
六边形的外角和
知识精讲
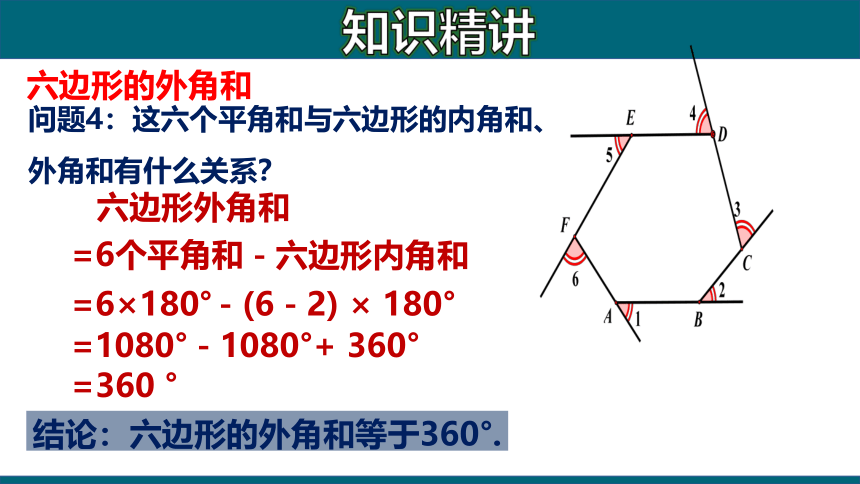
六边形外角和
=360 °
=6个平角和
-六边形内角和
=6×180°
-(6-2) × 180°
问题4:这六个平角和与六边形的内角和、外角和有什么关系?
结论:六边形的外角和等于360°.
=1080°-1080°+ 360°
六边形的外角和
知识精讲
因此,小赵沿一个六边形花坛,按逆时针方向跑步,每跑一圈回到原点,需要转过360°
知识精讲
1、你知道四边形的外角和是多少度吗?
2、五边形的外角和是多少度?
E
B
C
D
1
2
3
4
5
A
知识精讲
知识精讲
结论:多边形的外角和等 于360°
与边数 无关
An
A2
A3
A4
1
2
3
4
n
A1
典例解析
例1、已知四边形的四个外角度数比为1∶2∶3∶4,求各外角的度数
由四边形外角和与各外角之间的比例关系可求出各外角
分析:
解:设四边形的最小外角为x ° ,则其他三个外角分
别为2x ° , 3x ° ,4x °.
根据四边形外角和等于360°,得
x ° +2x ° +3x ° +4x ° =360°
解得:x=36
∴2x ° =72°,3x ° =108°,4x ° =144°
∴四边形各外角度数分别为36°,72°,108°, 144°.
不列方程有其他解法吗?
典例解析
解:设这个多边形是n边形,
则它的内角和是 (n-2) 180°,
外角和等于 360°
依题意得 (n-2) ×180°=3×360°
解得:n=8
解:
分析:多边形的内角和与边数有关,外角和恒等于360°
用多边形外角和求多边形的边数,一般可利用方程思想通过列方程解决
∴这个多边形是八边形。
例2、一个多边形的内角和等于它的外角和的3倍,它是几边形?
典例解析
巩固训练
1、正五边形的每一个外角等于___°.
【分析:正n边形的每个外角的度数为360? /n,
即已知正多边形的边数,可以求各相等外角的度数,反之亦可】
72
2、如图,小亮从A点出发,沿直线前进10 m后向左转30°,再沿直线前进10 m,又向左转30°……照这样走下去,小亮第一次回到出发地A点时,他一共走了________m.
由题意知,当小亮第一次回到出发地A点时,每个外角都是30°的正多边形.由多边形的外角和定理知这个多边形的边数是
分析:
120
360°÷30°=12,
小亮每走一边长为10 m,
所以小亮一共走了10 × 12 =120 m。
巩固训练
小结梳理
1、多边形的外角及外角和的定义
多边形内角的一边与另一边的反向延长线所组成的角叫做这个多边形的外角.在每个顶点处取这个多边形的一个外角,它们的和叫做这个多边形的外角和.
2、多边形的外角和
多边形的外角和等于360°,与它的边数无关
3、正n边形的每个外角度数
正n边形的每个外角度数等于360? /n
学习目标
能利用外角和公式解决问题.
探索并求出多边形外角和.
情境引入
跑步可以强身健体,提高抵抗力。小赵沿一个六边形花坛,按逆时针方向跑步,每跑一圈回到原点,需要转过多少的角度?他都转过哪些角?
知识精讲
(1)小赵每从一条小路转到下一条小路时,跑步方向改变的角是哪个角?
分别是∠1,∠2,∠3,∠4,∠5,∠6
(2)求“他每跑一圈回到原点,需要转过多少的角度”,实际上是求什么?
∠1+∠2+∠3+∠4+∠5+∠6
思考
知识精讲
多边形内角一边与另一边的反向延长线所组成的角叫做多边形的一个外角.
在每个顶点处各取一个外角,这些外角的和叫做多边形的外角和.
如图,在六边形的每个顶点处各取
一个外角,这些外角的和叫做六边
形的外角和.
多边形的外角和
知识链接
1、n边形的内角和公式是什么?
(n-2)×180°
2、三角形的外角和是多少?你还记得这个结论是如何得出的吗?
360°
知识精讲
问题1:任意一个外角和它相邻的内角有什么关系?
互补
即 ∠1+∠FAB=180°,∠2+∠ABC=180°,
∠3+∠BCD=180°,∠4+∠CDE=180°,
∠5+∠DEF=180°,∠6+∠EFA=180°
六边形的外角和
知识精讲
问题2:六个外角加上它们分别相邻的六个内角和是多少?
6×180°
即6个平角的和
问题3:这个六边形的六个内角和是多少?
(6-2) ×180°
六边形的外角和
知识精讲
六边形外角和
=360 °
=6个平角和
-六边形内角和
=6×180°
-(6-2) × 180°
问题4:这六个平角和与六边形的内角和、外角和有什么关系?
结论:六边形的外角和等于360°.
=1080°-1080°+ 360°
六边形的外角和
知识精讲
因此,小赵沿一个六边形花坛,按逆时针方向跑步,每跑一圈回到原点,需要转过360°
知识精讲
1、你知道四边形的外角和是多少度吗?
2、五边形的外角和是多少度?
E
B
C
D
1
2
3
4
5
A
知识精讲
知识精讲
结论:多边形的外角和等 于360°
与边数 无关
An
A2
A3
A4
1
2
3
4
n
A1
典例解析
例1、已知四边形的四个外角度数比为1∶2∶3∶4,求各外角的度数
由四边形外角和与各外角之间的比例关系可求出各外角
分析:
解:设四边形的最小外角为x ° ,则其他三个外角分
别为2x ° , 3x ° ,4x °.
根据四边形外角和等于360°,得
x ° +2x ° +3x ° +4x ° =360°
解得:x=36
∴2x ° =72°,3x ° =108°,4x ° =144°
∴四边形各外角度数分别为36°,72°,108°, 144°.
不列方程有其他解法吗?
典例解析
解:设这个多边形是n边形,
则它的内角和是 (n-2) 180°,
外角和等于 360°
依题意得 (n-2) ×180°=3×360°
解得:n=8
解:
分析:多边形的内角和与边数有关,外角和恒等于360°
用多边形外角和求多边形的边数,一般可利用方程思想通过列方程解决
∴这个多边形是八边形。
例2、一个多边形的内角和等于它的外角和的3倍,它是几边形?
典例解析
巩固训练
1、正五边形的每一个外角等于___°.
【分析:正n边形的每个外角的度数为360? /n,
即已知正多边形的边数,可以求各相等外角的度数,反之亦可】
72
2、如图,小亮从A点出发,沿直线前进10 m后向左转30°,再沿直线前进10 m,又向左转30°……照这样走下去,小亮第一次回到出发地A点时,他一共走了________m.
由题意知,当小亮第一次回到出发地A点时,每个外角都是30°的正多边形.由多边形的外角和定理知这个多边形的边数是
分析:
120
360°÷30°=12,
小亮每走一边长为10 m,
所以小亮一共走了10 × 12 =120 m。
巩固训练
小结梳理
1、多边形的外角及外角和的定义
多边形内角的一边与另一边的反向延长线所组成的角叫做这个多边形的外角.在每个顶点处取这个多边形的一个外角,它们的和叫做这个多边形的外角和.
2、多边形的外角和
多边形的外角和等于360°,与它的边数无关
3、正n边形的每个外角度数
正n边形的每个外角度数等于360? /n
