人教版数学八年级上册11.3.2 多边形的内角和课件(共16张PPT)
文档属性
| 名称 | 人教版数学八年级上册11.3.2 多边形的内角和课件(共16张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-23 14:26:07 | ||
图片预览




文档简介
多边形的内角和
学习目标
探索多边形内角和公式.
利用多边形内角和公式解决简单问题.
知识精讲
问题2:你知道长方形和正方形的内角和是多少?
其它四边形的内角和是多少?
问题1:你还记得三角形内角和是多少度?
(三角形内角和 180°)
(都是360°)
想一想
知识精讲
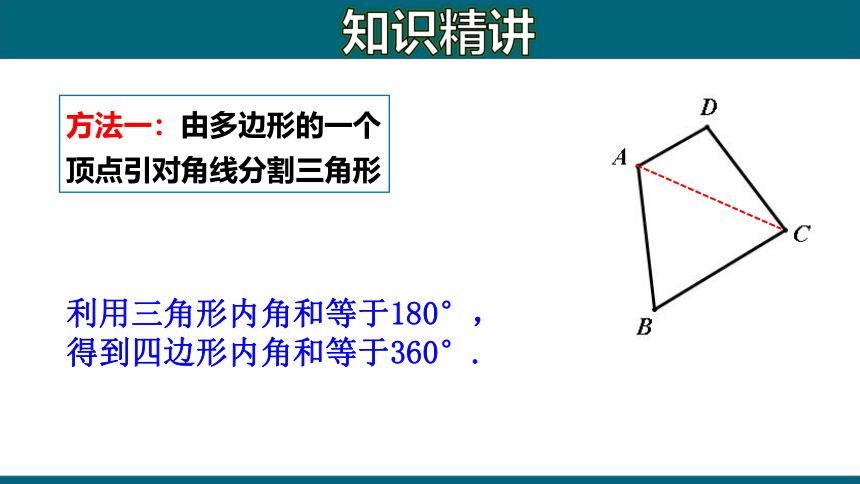
方法一:由多边形的一个顶点引对角线分割三角形
利用三角形内角和等于180°,得到四边形内角和等于360°.
知识精讲
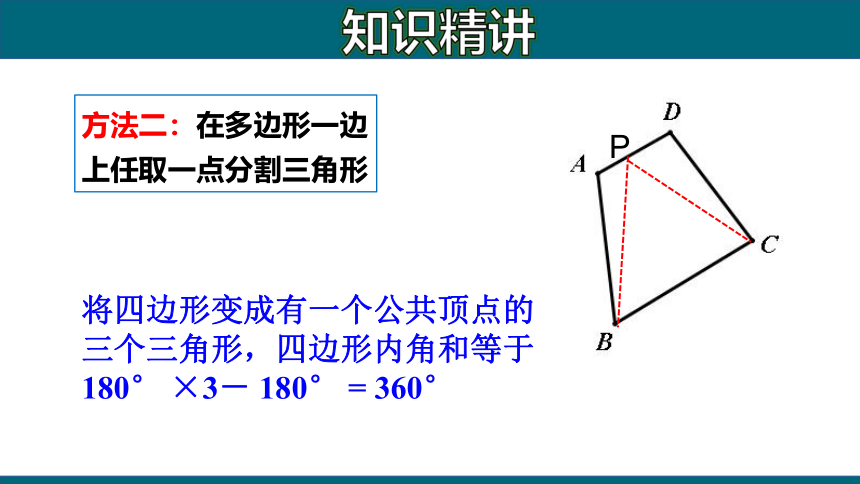
方法二:在多边形一边上任取一点分割三角形
P
将四边形变成有一个公共顶点的三个三角形,四边形内角和等于180° ×3- 180° = 360°
知识精讲
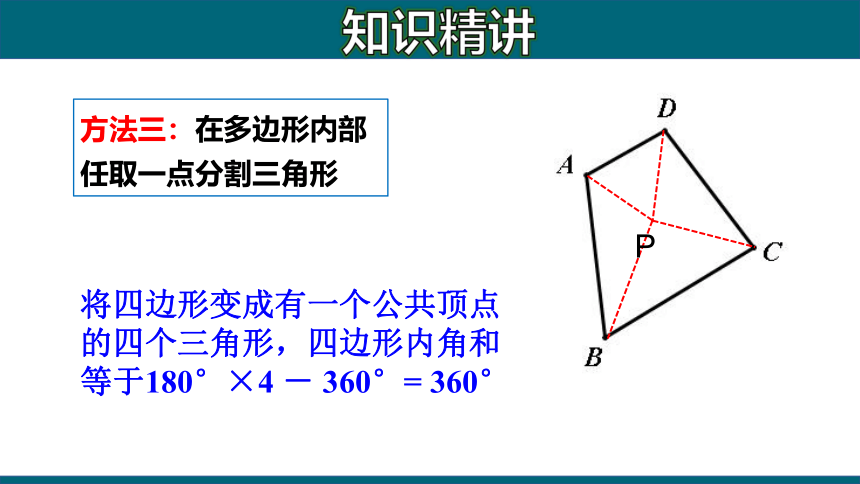
方法三:在多边形内部任取一点分割三角形
P
将四边形变成有一个公共顶点的四个三角形,四边形内角和等于180°×4 - 360°= 360°
知识精讲
你知道五边形的内角和吗?六边形呢?七边形呢?
请你选择喜欢的一种方法解答上述问题.
知识精讲
你知道五边形的内角和吗?六边形呢?七边形呢?
请你选择喜欢的一种方法解答上述问题.
知识精讲
多边形
边数
分成三角形的个数
图形
内角和
计算规律
三角形
四边形
五边形
六边形
七边形
n边形
…
…
…
…
…
…
3
4
5
6
7
n
1
n-2
2
3
4
5
180°
360°
540°
720°
900°
(n-2) ·180°
(n-2) ·180°
5 ×180°
4 ×180°
3 ×180°
2 ×180°
1 ×180°
知识精讲
n边形内角和公式:(n-2)180°
n边形共有对角线 条(n≥3)
n边形从一个顶点出发的对角线有(n-3)条(n≥3)
知识精讲
(2)已知一个多边形的内角和为720o ,则这个多边形是______边形
6
(3)在五边形ABCDE中,若∠A=∠D=90o,且
∠B:∠C:∠E=3:2:4,则∠C的度数为_______
80o
(1)求十边形的内角和的度数。
解:(10-2)×180°=8 ×180°=1440°
答:十边形的内角和是1440°
典例解析
过多边形一个顶点的所有对角线将这个多边形分成3个三角形,求:
(1)这个多边形的边数.
(2)这个多边形内角和的度数.
实际应用
3、填空(求边数)
1、已知一个多边形的内角和为1080°,则它的边数为__。
2、已知一个多边形的每一个内角都是156°,则它的边数为__。
8
15
知识精讲
例: 一个六边形如图,已知AB∥DE,BC∥EF,CD∥AF,求∠A+∠C+∠E的度数.
A
B
C
D
E
F
1
2
3
4
解:如图所示,连结AD,
∵AB∥DE, CD∥AF(已知)
∴∠1=∠3,∠2=∠4(两 直线平行,内错角相等)
∴∠1+∠2=∠3+∠4,
即∠FAB=∠CDE,同理∠B=∠E,∠C=∠F
∴∠FAB+∠C+∠E= 1/2 ×720°=360°
∵∠FAB+∠B+∠C+∠CDE+∠E+∠F
=(6-2)×180°= 720°
小结梳理
n边形的内角和为(n-2) ×180°(n≥3)
n边形从一个顶点出发的对角线有(n-3)条(n≥3)
n边形共有对角线 条(n≥3)
一种重要数学思想方法(转化思想)
对角线是解决多边形问题的常用辅助线
多边形问题 三角形问题
转化
(未知)
(已知)
1
2
3
学习目标
探索多边形内角和公式.
利用多边形内角和公式解决简单问题.
知识精讲
问题2:你知道长方形和正方形的内角和是多少?
其它四边形的内角和是多少?
问题1:你还记得三角形内角和是多少度?
(三角形内角和 180°)
(都是360°)
想一想
知识精讲
方法一:由多边形的一个顶点引对角线分割三角形
利用三角形内角和等于180°,得到四边形内角和等于360°.
知识精讲
方法二:在多边形一边上任取一点分割三角形
P
将四边形变成有一个公共顶点的三个三角形,四边形内角和等于180° ×3- 180° = 360°
知识精讲
方法三:在多边形内部任取一点分割三角形
P
将四边形变成有一个公共顶点的四个三角形,四边形内角和等于180°×4 - 360°= 360°
知识精讲
你知道五边形的内角和吗?六边形呢?七边形呢?
请你选择喜欢的一种方法解答上述问题.
知识精讲
你知道五边形的内角和吗?六边形呢?七边形呢?
请你选择喜欢的一种方法解答上述问题.
知识精讲
多边形
边数
分成三角形的个数
图形
内角和
计算规律
三角形
四边形
五边形
六边形
七边形
n边形
…
…
…
…
…
…
3
4
5
6
7
n
1
n-2
2
3
4
5
180°
360°
540°
720°
900°
(n-2) ·180°
(n-2) ·180°
5 ×180°
4 ×180°
3 ×180°
2 ×180°
1 ×180°
知识精讲
n边形内角和公式:(n-2)180°
n边形共有对角线 条(n≥3)
n边形从一个顶点出发的对角线有(n-3)条(n≥3)
知识精讲
(2)已知一个多边形的内角和为720o ,则这个多边形是______边形
6
(3)在五边形ABCDE中,若∠A=∠D=90o,且
∠B:∠C:∠E=3:2:4,则∠C的度数为_______
80o
(1)求十边形的内角和的度数。
解:(10-2)×180°=8 ×180°=1440°
答:十边形的内角和是1440°
典例解析
过多边形一个顶点的所有对角线将这个多边形分成3个三角形,求:
(1)这个多边形的边数.
(2)这个多边形内角和的度数.
实际应用
3、填空(求边数)
1、已知一个多边形的内角和为1080°,则它的边数为__。
2、已知一个多边形的每一个内角都是156°,则它的边数为__。
8
15
知识精讲
例: 一个六边形如图,已知AB∥DE,BC∥EF,CD∥AF,求∠A+∠C+∠E的度数.
A
B
C
D
E
F
1
2
3
4
解:如图所示,连结AD,
∵AB∥DE, CD∥AF(已知)
∴∠1=∠3,∠2=∠4(两 直线平行,内错角相等)
∴∠1+∠2=∠3+∠4,
即∠FAB=∠CDE,同理∠B=∠E,∠C=∠F
∴∠FAB+∠C+∠E= 1/2 ×720°=360°
∵∠FAB+∠B+∠C+∠CDE+∠E+∠F
=(6-2)×180°= 720°
小结梳理
n边形的内角和为(n-2) ×180°(n≥3)
n边形从一个顶点出发的对角线有(n-3)条(n≥3)
n边形共有对角线 条(n≥3)
一种重要数学思想方法(转化思想)
对角线是解决多边形问题的常用辅助线
多边形问题 三角形问题
转化
(未知)
(已知)
1
2
3
