人教版数学八年级上册第十一章 三角形 数学活动 镶嵌 课件(共29张PPT)
文档属性
| 名称 | 人教版数学八年级上册第十一章 三角形 数学活动 镶嵌 课件(共29张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-08-23 00:00:00 | ||
图片预览





文档简介
平面镶嵌
学习目标
理解平面镶嵌的概念
理解多边形进行平面镶嵌的条件
会利用平面镶嵌的条件设计简单的镶嵌方案
温故知新
1.多边形的内角和公式是 .
2.在下表中填入相应正多边形每个内角的度数.
正多边形的
边数
3
4
5
6
8
12
一个内角的
度数
知识精讲
生活中常常用瓷砖严丝合缝、不留空隙地铺满墙面或地面。从数学的角度看,就是用几何图形不留空隙、不重叠地铺满平面的一部分,这就是平面图形的镶嵌.
探究一
从正三角形、正方形、正五边形、正六边形中选用其中一种镶嵌,哪几种正多边形能够进行平面镶嵌?
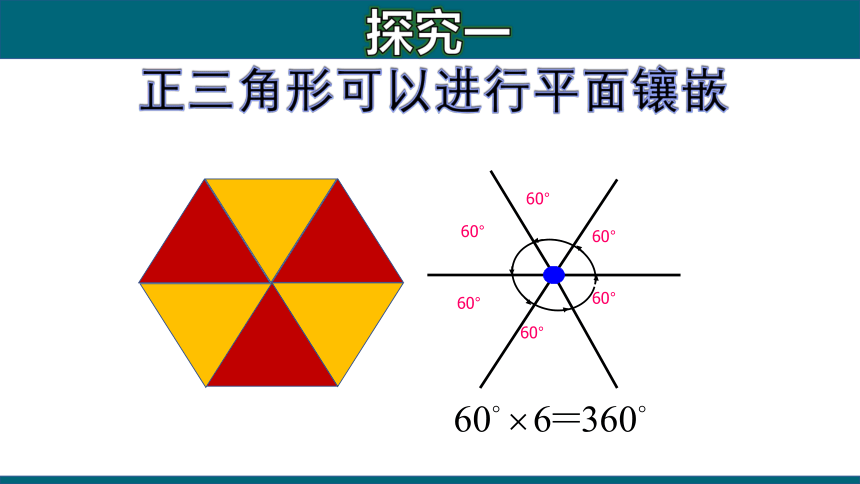
60°
60°
60°
60°
60°
60°
正三角形可以进行平面镶嵌
探究一
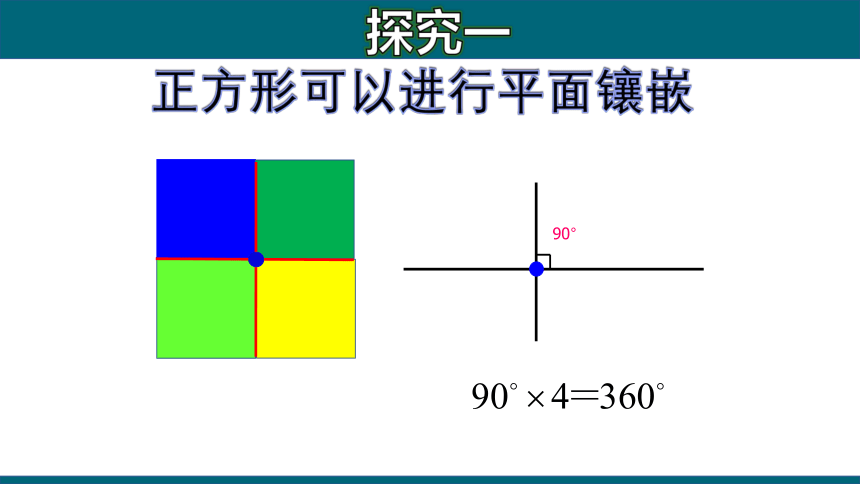
正方形可以进行平面镶嵌
90°
探究一
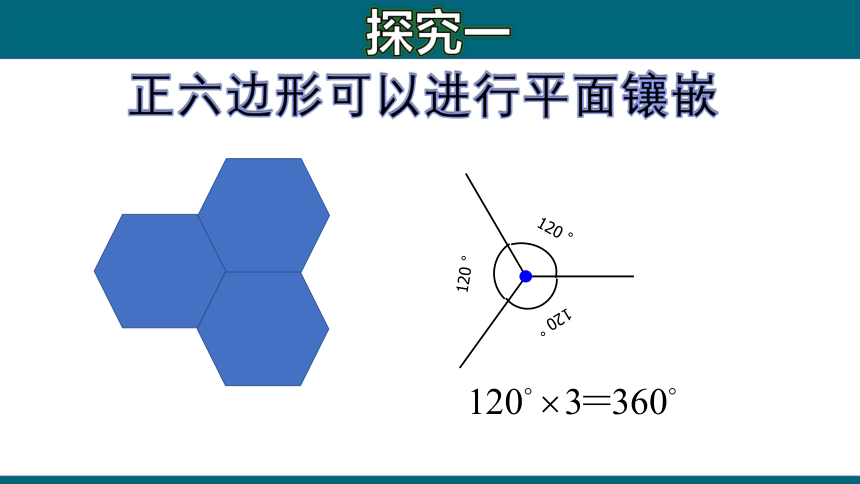
正六边形可以进行平面镶嵌
120 °
120 °
120 °
探究一
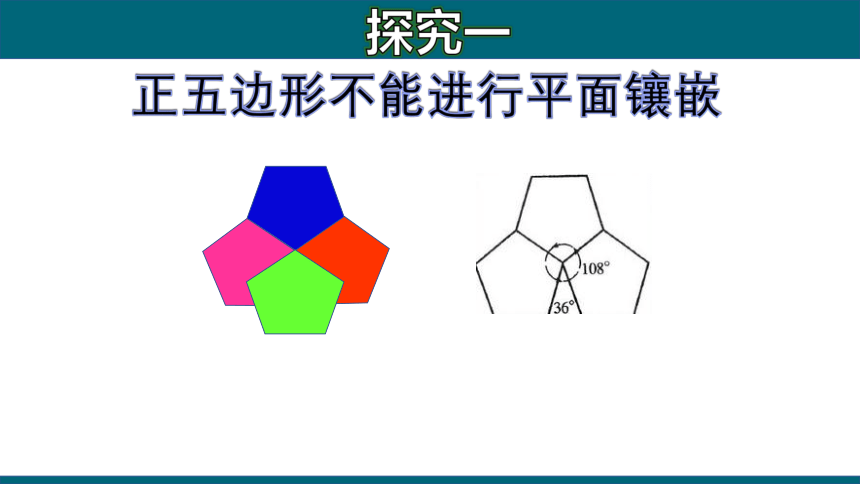
正五边形不能进行平面镶嵌
探究一
观察特例 发现规律
如果一种正多边形能单独进行平面镶嵌,那么它的一个内角的度数是360的约数.
如果用x 表示正多边形的一个内角的度数,a 表示正多边形的个数,那么上面的结论可表示为:ax =360.
探究一
只选用正八边形能进行平面镶嵌吗?
为什么?正十边形呢?
运用结论 思考判断
探究一
下表给出了一些正多边形一个内角的度数,请判别仅选用某一种正多边形,能否进行镶嵌?
正多边形的
边数
12
15
18
20
30
36
一个内角的
度数
类比探究 发现规律
探究一
归纳总结1
1.正三角形、正方形、正六边形能单独进行镶嵌,正五边形、正八边形等其他的正多边形都不能单独进行镶嵌.
2.如果能用某种正多边形单独进行镶嵌,那么它一内角的度数是360的约数.
(用数学式子表示为:ax =360,x 表示正多边形的每一个内角的度数,a 表示正多边形的个数.)
1)用若干个形状、大小相同的任意三角形能进行平面镶嵌吗?
1
3
2
探究二
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
∵ ∠1+∠2+∠3=180°
∴2(∠1+∠2+∠3)=360°
若干形状、大小相同的任意三角形可以进行平面镶嵌。
在拼接点处有 个角,这些角之和是三角形内角和的 倍,等于 °.
6
6
2
360
拼接在一起的两条边长度是 的.
相等
探究二
中考链接
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
若干形状、大小相同的任意三角形可以进行平面镶嵌.
2)用若干个形状、大小相同的任意四边形能进行平面镶嵌吗?
1
3
2
4
探究二
∠1+∠2+∠3+∠4=360°
1
4
3
2
1
4
3
2
1
4
3
2
1
4
3
2
若干形状、大小相同的任意四边形可以进行平面镶嵌.
探究二
1. 形状、大小相同的任意三角形可以进行平面镶嵌.
2. 形状、大小相同的任意四边形可以进行平面镶嵌.
3. 镶嵌时,在某一拼接点处拼接在一起的各角之和为360 °.拼接在一起的两条边相等.
归纳总结2
从下面边长相等的正多边形中选择两种进行平面镶嵌,你会选择哪两种?
①
②
③
有三种选择:①②、①③、②③
探究三
①
②
③
①②、①③、②③这三种方案都能进行平面镶嵌吗?
探究三
两种正多边形镶嵌的条件:
1.拼接在同一顶点处的各角之和恰好为360 °;如果用a,b分别表示两种正多边形的个数,用x、y分别表示两种正多边形一个内角的度数,则ax + by =360.
2.拼接在一起的两边相等.
观察特例 发现规律
探究三
同时选用边长相等的正方形与正六边形能进行平面镶嵌吗?
150 °
90 °
120 °
∟
探究三
判断:
1.用边长相等的正方形和正八边形能否进行镶嵌?
2.用边长相等的正三角形和正十二边形能否进行镶嵌?
火眼金睛 明察秋毫
探究三
正方形与正八边形可以进行镶嵌
探究三
正三角形与正十二边形可以进行镶嵌
探究三
1.边长相等的两种正多形进行平面镶嵌的方案有4种:
①正三角形与正方形;②正三角形与正六边形
③正三角形与正十二边形;④正方形与正八边形.
2.进行平面镶嵌的条件是:在同一拼接点处的各角之和恰好为 ,拼接在一起的两边 .
归纳总结3
小结梳理
谈一谈,通过本节课,你有哪些收获和体会?
1.平面镶嵌的定义;
2.平面镶嵌的条件;
3. 探索了从特殊多边形到一般多边形镶嵌的条件;
4.通过构建方程来探索两种正多边形镶嵌的规律.
学习目标
理解平面镶嵌的概念
理解多边形进行平面镶嵌的条件
会利用平面镶嵌的条件设计简单的镶嵌方案
温故知新
1.多边形的内角和公式是 .
2.在下表中填入相应正多边形每个内角的度数.
正多边形的
边数
3
4
5
6
8
12
一个内角的
度数
知识精讲
生活中常常用瓷砖严丝合缝、不留空隙地铺满墙面或地面。从数学的角度看,就是用几何图形不留空隙、不重叠地铺满平面的一部分,这就是平面图形的镶嵌.
探究一
从正三角形、正方形、正五边形、正六边形中选用其中一种镶嵌,哪几种正多边形能够进行平面镶嵌?
60°
60°
60°
60°
60°
60°
正三角形可以进行平面镶嵌
探究一
正方形可以进行平面镶嵌
90°
探究一
正六边形可以进行平面镶嵌
120 °
120 °
120 °
探究一
正五边形不能进行平面镶嵌
探究一
观察特例 发现规律
如果一种正多边形能单独进行平面镶嵌,那么它的一个内角的度数是360的约数.
如果用x 表示正多边形的一个内角的度数,a 表示正多边形的个数,那么上面的结论可表示为:ax =360.
探究一
只选用正八边形能进行平面镶嵌吗?
为什么?正十边形呢?
运用结论 思考判断
探究一
下表给出了一些正多边形一个内角的度数,请判别仅选用某一种正多边形,能否进行镶嵌?
正多边形的
边数
12
15
18
20
30
36
一个内角的
度数
类比探究 发现规律
探究一
归纳总结1
1.正三角形、正方形、正六边形能单独进行镶嵌,正五边形、正八边形等其他的正多边形都不能单独进行镶嵌.
2.如果能用某种正多边形单独进行镶嵌,那么它一内角的度数是360的约数.
(用数学式子表示为:ax =360,x 表示正多边形的每一个内角的度数,a 表示正多边形的个数.)
1)用若干个形状、大小相同的任意三角形能进行平面镶嵌吗?
1
3
2
探究二
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
∵ ∠1+∠2+∠3=180°
∴2(∠1+∠2+∠3)=360°
若干形状、大小相同的任意三角形可以进行平面镶嵌。
在拼接点处有 个角,这些角之和是三角形内角和的 倍,等于 °.
6
6
2
360
拼接在一起的两条边长度是 的.
相等
探究二
中考链接
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
若干形状、大小相同的任意三角形可以进行平面镶嵌.
2)用若干个形状、大小相同的任意四边形能进行平面镶嵌吗?
1
3
2
4
探究二
∠1+∠2+∠3+∠4=360°
1
4
3
2
1
4
3
2
1
4
3
2
1
4
3
2
若干形状、大小相同的任意四边形可以进行平面镶嵌.
探究二
1. 形状、大小相同的任意三角形可以进行平面镶嵌.
2. 形状、大小相同的任意四边形可以进行平面镶嵌.
3. 镶嵌时,在某一拼接点处拼接在一起的各角之和为360 °.拼接在一起的两条边相等.
归纳总结2
从下面边长相等的正多边形中选择两种进行平面镶嵌,你会选择哪两种?
①
②
③
有三种选择:①②、①③、②③
探究三
①
②
③
①②、①③、②③这三种方案都能进行平面镶嵌吗?
探究三
两种正多边形镶嵌的条件:
1.拼接在同一顶点处的各角之和恰好为360 °;如果用a,b分别表示两种正多边形的个数,用x、y分别表示两种正多边形一个内角的度数,则ax + by =360.
2.拼接在一起的两边相等.
观察特例 发现规律
探究三
同时选用边长相等的正方形与正六边形能进行平面镶嵌吗?
150 °
90 °
120 °
∟
探究三
判断:
1.用边长相等的正方形和正八边形能否进行镶嵌?
2.用边长相等的正三角形和正十二边形能否进行镶嵌?
火眼金睛 明察秋毫
探究三
正方形与正八边形可以进行镶嵌
探究三
正三角形与正十二边形可以进行镶嵌
探究三
1.边长相等的两种正多形进行平面镶嵌的方案有4种:
①正三角形与正方形;②正三角形与正六边形
③正三角形与正十二边形;④正方形与正八边形.
2.进行平面镶嵌的条件是:在同一拼接点处的各角之和恰好为 ,拼接在一起的两边 .
归纳总结3
小结梳理
谈一谈,通过本节课,你有哪些收获和体会?
1.平面镶嵌的定义;
2.平面镶嵌的条件;
3. 探索了从特殊多边形到一般多边形镶嵌的条件;
4.通过构建方程来探索两种正多边形镶嵌的规律.
